Natural Transformation 

そろそろ自然性にチャレンジできるぐらい経験値を積んだだろうか。本の中程 7.4節まで飛ばしてみよう。

自然変換 (natural transformation) は函手の射だ。その通り。与えられた圏 C と D について、函手 C => D を新たな圏の「対象」として考えて、これらの対象間の射を自然変換と呼ぶことにする。

Scala での自然変換に関していくつか面白い記事が書かれている:

• Higher-Rank Polymorphism in Scala, Rúnar (@runarorama) July 2, 2010
• Type-Level Programming in Scala, Part 7: Natural transformation literals, Mark Harrah (@harrah) October 26, 2010
• First-class polymorphic function values in shapeless (2 of 3) — Natural Transformations in Scala, Miles Sabin (@milessabin) May 10, 2012

Mark さんがシンプルな具体例を挙げて自然変換が何故必要なのかを説明している:

自然変換に進むと問題に直面する。例えば、全ての T に関して Option[T] を List[T] へと投射する関数は定義することはできない。これが自明でなければ、以下がコンパイルするような toList を定義してみよう:

val toList = ...
 
val a: List[Int] = toList(Some(3))
assert(List(3) == a)
 
val b: List[Boolean] = toList(Some(true))
assert(List(true) == b)

自然変換 M ~> N (ここでは M=Option、N=List) を定義するには、暗黙のクラスを作る必要がある。Scala には量化された関数 (quantified function) を定義するリテラルが無いからだ。

これは Scalaz に移植されている。NaturalTransformation をみてみよう:

/** A universally quantified function, usually written as `F ~> G`,
  * for symmetry with `A => B`.
  * ....
  */
trait NaturalTransformation[-F[_], +G[_]] {
  self =>
  def apply[A](fa: F[A]): G[A]

  ....
}

シンボルを使ったエイリアスは scalaz 名前空間の package object 内にて定義されている:

  /** A [[scalaz.NaturalTransformation]][F, G]. */
  type ~>[-F[_], +G[_]] = NaturalTransformation[F, G]
  /** A [[scalaz.NaturalTransformation]][G, F]. */
  type <~[+F[_], -G[_]] = NaturalTransformation[G, F]

toList を定義してみる:

scala> val toList = new (Option ~> List) {
         def apply[T](opt: Option[T]): List[T] =
           opt.toList
       }
toList: scalaz.~>[Option,List] = 1@2fdb237

scala> toList(3.some)
res17: List[Int] = List(3)

scala> toList(true.some)
res18: List[Boolean] = List(true)

これを圏論の用語を比較してみると、Scalaz の世界では List や Option のような型コンストラクタは 2つの圏を map する Functor をサポートしている。

trait Functor[F[_]] extends InvariantFunctor[F] { self =>
  ////

  /** Lift `f` into `F` and apply to `F[A]`. */
  def map[A, B](fa: F[A])(f: A => B): F[B]
  ...
}

これは、より一般的な C => D に比べてかなり限定的な函手だと言えるが、型コンストラクタを圏と考えれば確かに函手ではある。

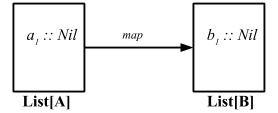
NaturalTransformation (~>) が型コンストラクタ (一次カインド型) のレベルではたらくため、それは函手間の射 (または圏の間の射のファミリー) だと言える。

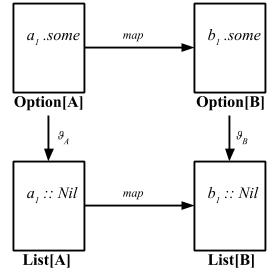
続きはまたここから。