圏の例 

抽象的に行く前に具象圏をいくつか紹介する。昨日は一つの圏の話しかしてこなかったので、これは役に立つことだと思う。

Sets 

集合と全域関数の圏は太字で Sets と表記する。

Sets_fin 

全ての有限集合とその間の全域関数を Sets_fin という。今まで見てきた圏がこれだ。

Pos 

Awodey も和訳が見つからなかったので勝手訳になる:

数学でよく見るものに構造的集合 (structured set)、つまり集合に何らかの「構造」を追加したものと、それを「保存する」関数の圏というものがある。（構造と保存の定義は独自に与えられる）

半順序集合 (partially ordered set)、または略して poset と呼ばれる集合 A は、全ての a, b, c ∈ A に対して以下の条件が成り立つ二項関係 a ≤_A b を持つ:

• 反射律 (reflexivity): a ≤_A a
• 推移律 (transitivity): もし a ≤_A b かつ b ≤_A c ならば a ≤_A c
• 反対称律 (antisymmetry): もし a ≤_A b かつ b ≤_A a ならば a = b

poset A から poset B への射は単調 (monotone) な関数 m: A => B で、これは全ての a, a’ ∈ A に対して以下が成り立つという意味だ:

• a ≤_A a’ のとき m(a) ≤_A m(a’)

関数が単調 (monotone) であるかぎり対象は圏の中にとどまるため、「構造」が保存されると言える。poset と単調関数の圏は Pos と表記される。Awodey は poset が好きなので、これを理解しておくのは重要。

Cat 

定義 1.2. 函手 (functor)
F: C => D
は、圏 C と圏 D の間で以下の条件が成り立つように対象を対象に、また射を射に転写する:

• F(f: A => B) = F(f): F(A) => F(B)
• F(1_A) = 1_F(A)
• F(g ∘ f) = F(g) ∘ F(f)

つまり、F はドメインとコドメイン、恒等射、および射の合成を保存する。

ついにきた。函手 (functor) は 2つの圏の間の射だ。以下が外部図式となる:

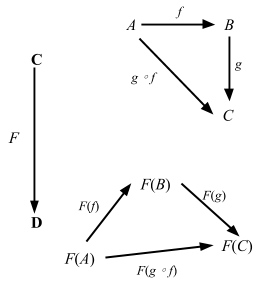
F(A)、 F(B)、 F(C) の位置が歪んでいるのは意図的なものだ。F は上の図を少し歪ませているけども、射の合成関係は保存している。

この圏と函手の圏は Cat と表記される。

モノイド 

モノイド (単位元を持つ半群とも呼ばれる) は、集合 M で、二項演算 ·: M × M => M と特定の「単位元」(unit) u ∈ M を持ち、任意の x, y, z ∈ M に対して以下の条件を満たすもの:

• x · (y · z) = (x · y) · z
• u · x = x = x · u

同義として、モノイドは唯一つの対象を持つ圏である。その圏の射はモノイドの要素だ。特に恒等射は単位元 u である。射の合成はモノイドの二項演算 m · n だ。

モノイドの概念は Scalaz にうまく翻訳できる。3日目のMonoid についてを見てほしい。

trait Monoid[A] extends Semigroup[A] { self =>
  ////
  /** The identity element for `append`. */
  def zero: A
  
  ...
}

trait Semigroup[A]  { self =>
  def append(a1: A, a2: => A): A
  ...
}

Int の加算と 0 はこうなる:

scala> 10 |+| Monoid[Int].zero
res26: Int = 10

Int の乗算と 1:

scala>  Tags.Multiplication(10) |+| Monoid[Int @@ Tags.Multiplication].zero
res27: scalaz.@@[Int,scalaz.Tags.Multiplication] = 10

このモノイドがただ一つの対象を持つ圏という考え方は「何を言っているんだ」と前は思ったものだけど、単集合を見ているので今なら理解できる気がする。

Mon 

モノイドとモノイドの構造を保存した関数の圏は Mon と表記される。このような構造を保存する射は準同型写像 (homomorphism) と呼ばれる。

モノイド M からモノイド N への準同型写像は、関数 h: M => N で全ての m, n ∈ M について以下の条件を満たすも

• h(m ·_M n) = h(m) ·_N h(n)
• h(u_M) = u_N

それぞれのモノイドは圏なので、モノイド準同型写像は函手の特殊形だと言える。

Groups 

定義 1.4 群 (group) G は、モノイドのうち全ての要素 g に対して逆射 g^-1 を持つもの。つまり、G は唯一つの対象を持つ圏で、全ての射が同型射となっている。

群と群の準同型写像の圏は Groups と表記される。

Scalaz に以前は群があったみたいだけど、一年ぐらい前に Spire とカブっているという理由で #279 にて削除された。