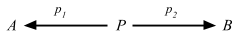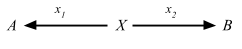0日目
1. 多相性って何?
2. sum 関数
3. FoldLeft
4. メソッド注入 (enrich my library)
1日目
1. sbt
2. Equal
3. Order
4. Show
5. Read
6. Enum
7. Bounded
8. Num
9. 型クラス中級講座
10. Yes と No の型クラス
2日目
1. Functor
2. Applicative
3日目
1. 型を司るもの、カインド
2. Tagged type
3. Monoid について
4日目
1. Functor則
2. Monoid としての Option
3. Foldable
5日目
1. モナドがいっぱい
2. 綱渡り
3. List モナド
4. MonadPlus と guard 関数
5. 騎士の旅
6. Monad則
6日目
1. Writer? 中の人なんていません!
2. Reader
7日目
1. Applicative Builder
2. 計算の状態の正体
3. \/
4. Validation
8日目
1. 便利なモナディック関数特集
2. 安全な RPN 電卓を作ろう
3. モナディック関数の合成
4. モナドを作る
9日目
1. Tree
2. Zipper
3. Id
4. 無法者の型クラス
10日目
1. モナド変換子
11日目
1. Lens
12日目
1. Origami programming
2. The Essence of the Iterator Pattern
13日目 (import ガイド)
14日目
15日目
1. Arrow
2. Unapply
3. 並列合成
16日目
1. Memo
2. 関数型プログラミング
3. エフェクトシステム
17日目
1. IO モナド
2. Enumeration-Based I/O with Iteratees
18日目
1. Func
2. Free Monad
3. Stackless Scala with Free Monads
19日目
1. 圏論
2. 点
3. 同型射
4. 決定問題と選択問題
20日目
1. 圏の例
2. 始対象と終対象
3. 積
4. 双対性
21日目
1. 余積
2. Hom 集合
3. Natural Transformation
読んでくれてありがとう
Scalaz cheatsheet

独習 Scalaz

これまでいくつのプログラミング言語が羊の衣を着た Lisp に喩えられただろうか? Java は馴染み親しんだ C++ のような文法に GC を持ち込んだ。それまで他にも GC を載せた言語はあったけども、現実的に C++ の代替となりうる言語に GC が載ったことは 1996年には画期的に思われた。やがて時は経ち、人々は自分でメモリ管理をしないことに慣れていった。JavaScript と Ruby の両言語もその第一級関数 (first-class function) やブロック構文を持つことから羊の衣を着た Lisp と呼ばれたことがある。S式の同図像性がマクロに適することから Lisp系の言語はまだ面白いと思う。

近年の言語はもう少し新しい関数型言語から概念を借りるようになってきた。型推論やパターンマッチングは ML にさかのぼることができると思う。時が経てば、人々はこれらの機能もまた当然と思うようになるだろう。Lisp が 1958年、ML が 1973年に発表されたことを考えると、良いアイディアが一般受けするには何十年かの時間がかかっている。その寒々しい何十年かの間、これらの言語は教義に異を唱える異端者、またはより酷く「真剣じゃない」と思われたことだろう。

別に Scalaz が次に大流行すると言っているわけじゃない。だいたい僕は Scalaz のことをまだ分かってもいない。ただ確信を持っているのはこれを使っている奴らは彼らの問題を真剣になって解いているということだ。または、残りの Scala コミュニティーがパターンマッチングを使っているのと同じぐらい学術的なことをやっている。Haskell が 1990年に発表されたことを考えると、この魔女裁判はしばらく続くだろうが、僕はオープンマインドでありたい。

リンク

Scalaz 7.0 ベースの古い独習 Scalaz
learning-scalaz.pdf

0日目

「(読者が) X日で学ぶ Scalaz」を書くつもりは無かった。1日目は、Scalaz 7 が milestone 7 だった 2012年の8月31日に書かれた。2日目はその次の日に書かれた。つまり、これは「(僕が) 独習」した web ログだ。だから、簡潔に最低限のことしか書かれてなかったりする。記事を書くよりも本を読みながらコードを試してみるのに時間をさいていた日もあったと思う。

いきなり詳細に飛び込む代わりに、今日は前編として導入から始めたいと思う。これは飛ばして後で読んでも構わない。

Scalaz 入門

Scalaz 入門はいくつかあるけど、僕が見た中で一番良かったのは Nick Partridge さんが Melbourne Scala Users Group で 2010年3月22日に行った Scalaz のトークだ。

Scalaz talk is up - http://bit.ly/c2eTVR Lots of code showing how/why the library exists
— Nick Partridge (@nkpart) March 28, 2010

これをネタとして使うことにする。

Scalaz は主に3つの部分から構成される:

新しいデータ型 (Validation、NonEmptyList など)
標準クラスの拡張 (OptionOps、ListOps など)
実用上必要な全ての汎用関数の実装 (アドホック多相性、trait + implicit)

多相性って何?

パラメータ多相

Nick さん曰く:

この関数 head は A のリストを取って A を返します。A が何であるかはかまいません。Int でもいいし、String でもいいし、Orange でも Car でもいいです。どの A でも動作し、存在可能な全ての A に対してこの関数は定義されています。

scala> def head[A](xs: List[A]): A = xs(0)
head: [A](xs: List[A])A

scala> head(1 :: 2 :: Nil)
res0: Int = 1

scala> case class Car(make: String)
defined class Car

scala> head(Car("Civic") :: Car("CR-V") :: Nil)
res1: Car = Car(Civic)

Haskell wiki 曰く:

パラメータ多相 (parametric polymorphism) とは、ある値の型が 1つもしくは複数の (制限の無い) 型変数を含むことを指し、その値は型変数を具象型によって置換することによって得られる型ならどれでも採用することができる。

派生型多態

ここで、型 A の 2つの値を足す plus という関数を考える:

scala> def plus[A](a1: A, a2: A): A = ???
plus: [A](a1: A, a2: A)A

型 A によって、足すことの定義を別々に提供する必要がある。これを実現する方法の一つが派生型 (subtyping) だ。

scala> trait Plus[A] {
         def plus(a2: A): A
       }
defined trait Plus

scala> def plus[A <: Plus[A]](a1: A, a2: A): A = a1.plus(a2)
plus: [A <: Plus[A]](a1: A, a2: A)A

これで A の型によって異なる plus の定義を提供できるようにはなった。しかし、この方法はデータ型の定義時に Plus を mixin する必要があるため柔軟性に欠ける。例えば、Int や String には使うことができない。

アドホック多相

Scala における3つ目の方法は trait への暗黙の変換か暗黙のパラメータ (implicit parameter) を使うことだ。

scala> trait Plus[A] {
         def plus(a1: A, a2: A): A
       }
defined trait Plus

scala> def plus[A: Plus](a1: A, a2: A): A = implicitly[Plus[A]].plus(a1, a2)
plus: [A](a1: A, a2: A)(implicit evidence$1: Plus[A])A

これは以下の意味においてまさにアドホックだと言える

異なる A の型に対して別の関数定義を提供することができる
(Int のような) 型に対してソースコードへのアクセスが無くても関数定義を提供することができる
異なるスコープにおいて関数定義を有効化したり無効化したりできる

この最後の点によって Scala のアドホック多相性は Haskell のそれよりもより強力なものだと言える。このトピックに関しては Debasish Ghosh さん (@debasishg) のScala Implicits: 型クラス、襲来参照。

この plus 関数をより詳しく見ていこう。

sum 関数

アドホック多相の具体例として、Int のリストを合計する簡単な関数 sum を徐々に一般化していく。

scala> def sum(xs: List[Int]): Int = xs.foldLeft(0) { _ + _ }
sum: (xs: List[Int])Int

scala> sum(List(1, 2, 3, 4))
res3: Int = 10

Monoid

これを少し一般化してみましょう。Monoid というものを取り出します。… これは、同じ型の値を生成する mappend という関数と「ゼロ」を生成する関数を含む型です。

scala> object IntMonoid {
         def mappend(a: Int, b: Int): Int = a + b
         def mzero: Int = 0
       }
defined module IntMonoid

これを代入することで、少し一般化されました。

scala> def sum(xs: List[Int]): Int = xs.foldLeft(IntMonoid.mzero)(IntMonoid.mappend)
sum: (xs: List[Int])Int

scala> sum(List(1, 2, 3, 4))
res5: Int = 10

次に、全ての型 A について Monoid が定義できるように、Monoid を抽象化します。これで IntMonoid が Int のモノイドになりました。

scala> trait Monoid[A] {
         def mappend(a1: A, a2: A): A
         def mzero: A
       }
defined trait Monoid

scala> object IntMonoid extends Monoid[Int] {
         def mappend(a: Int, b: Int): Int = a + b
         def mzero: Int = 0
       }
defined module IntMonoid

これで sum が Int のリストと Int のモノイドを受け取って合計を計算できるようになった:

scala> def sum(xs: List[Int], m: Monoid[Int]): Int = xs.foldLeft(m.mzero)(m.mappend)
sum: (xs: List[Int], m: Monoid[Int])Int

scala> sum(List(1, 2, 3, 4), IntMonoid)
res7: Int = 10

これで Int を使わなくなったので、全ての Int を一般型に置き換えることができます。

scala> def sum[A](xs: List[A], m: Monoid[A]): A = xs.foldLeft(m.mzero)(m.mappend)
sum: [A](xs: List[A], m: Monoid[A])A

scala> sum(List(1, 2, 3, 4), IntMonoid)
res8: Int = 10

最後の変更点は Monoid を implicit にすることで毎回渡さなくてもいいようにすることです。

scala> def sum[A](xs: List[A])(implicit m: Monoid[A]): A = xs.foldLeft(m.mzero)(m.mappend)
sum: [A](xs: List[A])(implicit m: Monoid[A])A

scala> implicit val intMonoid = IntMonoid
intMonoid: IntMonoid.type = IntMonoid$@3387dfac

scala> sum(List(1, 2, 3, 4))
res9: Int = 10

Nick さんはやらなかったけど、この形の暗黙のパラメータは context bound で書かれることが多い:

scala> def sum[A: Monoid](xs: List[A]): A = {
         val m = implicitly[Monoid[A]]
         xs.foldLeft(m.mzero)(m.mappend)
       }
sum: [A](xs: List[A])(implicit evidence$1: Monoid[A])A

scala> sum(List(1, 2, 3, 4))
res10: Int = 10

これでどのモノイドのリストでも合計できるようになり、 sum 関数はかなり一般化されました。String の Monoid を書くことでこれをテストすることができます。また、これらは Monoid という名前のオブジェクトに包むことにします。その理由は Scala の implicit 解決ルールです。ある型の暗黙のパラメータを探すとき、Scala はスコープ内を探しますが、それには探している型のコンパニオンオブジェクトも含まれるのです。

scala> :paste
// Entering paste mode (ctrl-D to finish)

trait Monoid[A] {
  def mappend(a1: A, a2: A): A
  def mzero: A
}
object Monoid {
  implicit val IntMonoid: Monoid[Int] = new Monoid[Int] {
    def mappend(a: Int, b: Int): Int = a + b
    def mzero: Int = 0
  }
  implicit val StringMonoid: Monoid[String] = new Monoid[String] {
    def mappend(a: String, b: String): String = a + b
    def mzero: String = ""
  }
}
def sum[A: Monoid](xs: List[A]): A = {
  val m = implicitly[Monoid[A]]
  xs.foldLeft(m.mzero)(m.mappend)
}

// Exiting paste mode, now interpreting.

defined trait Monoid
defined module Monoid
sum: [A](xs: List[A])(implicit evidence$1: Monoid[A])A

scala> sum(List("a", "b", "c"))
res12: String = abc

この関数に直接異なるモノイドを渡すこともできます。例えば、Int の積算のモノイドのインスタンスを提供してみましょう。

scala> val multiMonoid: Monoid[Int] = new Monoid[Int] {
         def mappend(a: Int, b: Int): Int = a * b
         def mzero: Int = 1
       }
multiMonoid: Monoid[Int] = $anon$1@48655fb6

scala> sum(List(1, 2, 3, 4))(multiMonoid)
res14: Int = 24

FoldLeft

List に関しても一般化した関数を目指しましょう。… そのためには、foldLeft 演算に関して一般化します。

scala> object FoldLeftList {
         def foldLeft[A, B](xs: List[A], b: B, f: (B, A) => B) = xs.foldLeft(b)(f)
       }
defined module FoldLeftList

scala> def sum[A: Monoid](xs: List[A]): A = {
         val m = implicitly[Monoid[A]]
         FoldLeftList.foldLeft(xs, m.mzero, m.mappend)
       }
sum: [A](xs: List[A])(implicit evidence$1: Monoid[A])A

scala> sum(List(1, 2, 3, 4))
res15: Int = 10

scala> sum(List("a", "b", "c"))
res16: String = abc

scala> sum(List(1, 2, 3, 4))(multiMonoid)
res17: Int = 24

これで先ほどと同様の抽象化を行なって FoldLeft 型クラスを抜き出します。

scala> :paste
// Entering paste mode (ctrl-D to finish)

trait FoldLeft[F[_]] {
  def foldLeft[A, B](xs: F[A], b: B, f: (B, A) => B): B
}
object FoldLeft {
  implicit val FoldLeftList: FoldLeft[List] = new FoldLeft[List] {
    def foldLeft[A, B](xs: List[A], b: B, f: (B, A) => B) = xs.foldLeft(b)(f)
  }
}

def sum[M[_]: FoldLeft, A: Monoid](xs: M[A]): A = {
  val m = implicitly[Monoid[A]]
  val fl = implicitly[FoldLeft[M]]
  fl.foldLeft(xs, m.mzero, m.mappend)
}

// Exiting paste mode, now interpreting.

warning: there were 2 feature warnings; re-run with -feature for details
defined trait FoldLeft
defined module FoldLeft
sum: [M[_], A](xs: M[A])(implicit evidence$1: FoldLeft[M], implicit evidence$2: Monoid[A])A

scala> sum(List(1, 2, 3, 4))
res20: Int = 10

scala> sum(List("a", "b", "c"))
res21: String = abc

これで Int と List の両方が sum から抜き出された。

Scalaz の型クラス

上の例における trait の Monoid と FoldLeft は Haskell の型クラスに相当する。Scalaz は多くの型クラスを提供する。

これらの型クラスの全ては必要な関数だけを含んだ部品に分けられています。ある関数が必要十分なものだけを要請するため究極のダック・タイピングだと言うこともできるでしょう。

メソッド注入 (enrich my library)

Monoid を使ってある型の 2つの値を足す関数を書いた場合、このようになります。

scala> def plus[A: Monoid](a: A, b: A): A = implicitly[Monoid[A]].mappend(a, b)
plus: [A](a: A, b: A)(implicit evidence$1: Monoid[A])A

scala> plus(3, 4)
res25: Int = 7

これに演算子を提供したい。だけど、1つの型だけを拡張するんじゃなくて、Monoid のインスタンスを持つ全ての型を拡張したい。Scalaz 7 スタイルでこれを行なってみる。

scala> trait MonoidOp[A] {
         val F: Monoid[A]
         val value: A
         def |+|(a2: A) = F.mappend(value, a2)
       }
defined trait MonoidOp

scala> implicit def toMonoidOp[A: Monoid](a: A): MonoidOp[A] = new MonoidOp[A] {
         val F = implicitly[Monoid[A]]
         val value = a
       }
toMonoidOp: [A](a: A)(implicit evidence$1: Monoid[A])MonoidOp[A]

scala> 3 |+| 4
res26: Int = 7

scala> "a" |+| "b"
res28: String = ab

1つの定義から Int と String の両方に |+| 演算子を注入することができた。

標準型構文

同様のテクニックを使って Scalaz は Option や Boolean のような標準ライブラリ型へのメソッド注入も提供する:

scala> 1.some | 2
res0: Int = 1

scala> Some(1).getOrElse(2)
res1: Int = 1

scala> (1 > 10)? 1 | 2
res3: Int = 2

scala> if (1 > 10) 1 else 2
res4: Int = 2

これで Scalaz がどういうライブラリなのかというのを感じてもらえただろうか。

1日目

型クラス初級講座

すごい Haskell たのしく学ぼう曰く:

型クラスは、何らかの振る舞いを定義するインターフェイスです。ある型クラスのインスタンスである型は、その型クラスが記述する振る舞いを実装します。

Scalaz 曰く:

It provides purely functional data structures to complement those from the Scala standard library. It defines a set of foundational type classes (e.g. Functor, Monad) and corresponding instances for a large number of data structures.

Scala 標準ライブラリを補完する純粋関数型データ構造を提供する。(Functor や Monad など) 基本的な型クラスを定義し、また多くのデータ構造に対して対応するインスタンスを提供する。

Haskell をたのしく学びながら Scalaz も学べるかためしてみよう。

sbt

以下が Scalaz 7.1.0 を試すための build.sbt だ:

scalaVersion := "2.11.2"

val scalazVersion = "7.1.0"

libraryDependencies ++= Seq(
  "org.scalaz" %% "scalaz-core" % scalazVersion,
  "org.scalaz" %% "scalaz-effect" % scalazVersion,
  "org.scalaz" %% "scalaz-typelevel" % scalazVersion,
  "org.scalaz" %% "scalaz-scalacheck-binding" % scalazVersion % "test"
)

scalacOptions += "-feature"

initialCommands in console := "import scalaz._, Scalaz._"

あとは sbt 0.12.3 から REPL を開くだけだ:

$ sbt console
...
[info] downloading http://repo1.maven.org/maven2/org/scalaz/scalaz-core_2.10/7.0.5/scalaz-core_2.10-7.0.5.jar ...
import scalaz._
import Scalaz._
Welcome to Scala version 2.10.3 (Java HotSpot(TM) 64-Bit Server VM, Java 1.6.0_51).
Type in expressions to have them evaluated.
Type :help for more information.

scala>

Scalaz 7.1.0 から生成された API ドキュメントもある。

Equal

LYAHFGG:

Eq は等値性をテストできる型に使われます。Eq のインスタンスが定義すべき関数は == と /= です。

Scalaz で Eq 型クラスと同じものは Equal と呼ばれている:

scala> 1 === 1
res0: Boolean = true

scala> 1 === "foo"
<console>:14: error: could not find implicit value for parameter F0: scalaz.Equal[Object]
              1 === "foo"
              ^

scala> 1 == "foo"
<console>:14: warning: comparing values of types Int and String using `==' will always yield false
              1 == "foo"
                ^
res2: Boolean = false

scala> 1.some =/= 2.some
res3: Boolean = true

scala> 1 assert_=== 2
java.lang.RuntimeException: 1 ≠ 2

標準の == のかわりに、Equal は equal メソッドを宣言することで ===、=/=、と assert_=== 演算を可能とする。主な違いは Int と String と比較すると === はコンパイルに失敗することだ。

注意: 初出ではここで =/= じゃなくて /== を使っていたけども、Eiríkr Åsheim さんに以下の通り教えてもらった:

@eed3si9n hey, was reading your scalaz tutorials. you should encourage people to use =/= and not /== since the latter has bad precedence.
— Eiríkr Åsheim (@d6) September 6, 2012

/== は優先順位壊れてるから =/= を推奨すべき。

通常、!= のような比較演算子は && や通常の文字列などに比べて高い優先順位を持つ。ところが、/== は = で終わるが = で始まらないため代入演算子のための特殊ルールが発動し、優先順位の最底辺に落ちてしまう:

scala> 1 != 2 && false
res4: Boolean = false

scala> 1 /== 2 && false
<console>:14: error: value && is not a member of Int
              1 /== 2 && false
                      ^

scala> 1 =/= 2 && false
res6: Boolean = false

Order

LYAHFGG:

Ord は、何らかの順序を付けられる型のための型クラスです。Ord はすべての標準的な大小比較関数、>、<、>=、 <= をサポートします。

Scalaz で Ord に対応する型クラスは Order だ:

scala> 1 > 2.0
res8: Boolean = false

scala> 1 gt 2.0
<console>:14: error: could not find implicit value for parameter F0: scalaz.Order[Any]
              1 gt 2.0
              ^

scala> 1.0 ?|? 2.0
res10: scalaz.Ordering = LT

scala> 1.0 max 2.0
res11: Double = 2.0

Order は Ordering (LT, GT, EQ) を返す ?|? 演算を可能とする。また、order メソッドを宣言することで lt、gt、lte、gte、min、そして max 演算子を可能とする。Equal 同様 Int と Double の比較はコンパイルを失敗させる。

Show

LYAHFGG:

ある値は、その値が Show 型クラスのインスタンスになっていれば、文字列として表現できます。

Scalaz で Show に対応する型クラスは Show だ:

scala> 3.show
res14: scalaz.Cord = 3

scala> 3.shows
res15: String = 3

scala> "hello".println
"hello"

Cord というのは潜在的に長い可能性のある文字列を保持できる純粋関数型データ構造のことらしい。

Read

LYAHFGG:

Read は Show と対をなす型クラスです。read 関数は文字列を受け取り、Read のインスタンスの型の値を返します。

これは対応する Scalaz での型クラスを見つけることができなかった。

Enum

LYAHFGG:

Enum のインスタンスは、順番に並んだ型、つまり要素の値を列挙できる型です。Enum 型クラスの主な利点は、その値をレンジの中で使えることです。また、Enum のインスタンスの型には後者関数 succ と前者関数 pred も定義されます。

Scalaz で Enum に対応する型クラスは Enum だ:

scala> 'a' to 'e'
res30: scala.collection.immutable.NumericRange.Inclusive[Char] = NumericRange(a, b, c, d, e)

scala> 'a' |-> 'e'
res31: List[Char] = List(a, b, c, d, e)

scala> 3 |=> 5
res32: scalaz.EphemeralStream[Int] = scalaz.EphemeralStreamFunctions$$anon$4@6a61c7b6

scala> 'B'.succ
res33: Char = C

Order 型クラスの上に pred と succ メソッドを宣言することで、標準の to のかわりに、Enum は List を返す |-> を可能とする。他にも -+-、---、from、 fromStep、pred、predx、succ、succx、|-->、|->、|==>、|=> など多くの演算があるが、全て前後にステップ移動するか範囲を返すものだ。

Bounded

Bounded 型クラスのインスタンスは上限と下限を持ち、それぞれ minBound と maxBound 関数で調べることができます。

Scalaz で Bounded に対応する型クラスは再び Enum みたいだ:

scala> implicitly[Enum[Char]].min
res43: Option[Char] = Some(?)

scala> implicitly[Enum[Char]].max
res44: Option[Char] = Some( )

scala> implicitly[Enum[Double]].max
res45: Option[Double] = Some(1.7976931348623157E308)

scala> implicitly[Enum[Int]].min
res46: Option[Int] = Some(-2147483648)

scala> implicitly[Enum[(Boolean, Int, Char)]].max
<console>:14: error: could not find implicit value for parameter e: scalaz.Enum[(Boolean, Int, Char)]
              implicitly[Enum[(Boolean, Int, Char)]].max
                        ^

Enum 型クラスのインスタンスは最大値に対して Option[T] を返す。

Num

Num は数の型クラスです。このインスタンスは数のように振る舞います。

Scalaz で Num、Floating、Integral に対応する型クラスは見つけることが出来なかった。

型クラス中級講座

Haskell の文法に関しては飛ばして第8章の型や型クラスを自分で作ろうまで行こう (本を持っている人は第7章)。

信号の型クラス

data TrafficLight = Red | Yellow | Green

これを Scala で書くと:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait TrafficLight
case object Red extends TrafficLight
case object Yellow extends TrafficLight
case object Green extends TrafficLight

これに Equal のインスタンスを定義する。

scala> implicit val TrafficLightEqual: Equal[TrafficLight] = Equal.equal(_ == _)
TrafficLightEqual: scalaz.Equal[TrafficLight] = scalaz.Equal$$anon$7@2457733b

使えるかな?

scala> Red === Yellow
<console>:18: error: could not find implicit value for parameter F0: scalaz.Equal[Product with Serializable with TrafficLight]
              Red === Yellow

Equal が不変 (invariant) なサブタイプ Equal[F] を持つせいで、Equal[TrafficLight] が検知されないみたいだ。TrafficLight を case class にして Red と Yellow が同じ型を持つようになるけど、厳密なパターンマッチングができなくなる。#ダメじゃん

scala> :paste
// Entering paste mode (ctrl-D to finish)

case class TrafficLight(name: String)
val red = TrafficLight("red")
val yellow = TrafficLight("yellow")
val green = TrafficLight("green")
implicit val TrafficLightEqual: Equal[TrafficLight] = Equal.equal(_ == _)
red === yellow

// Exiting paste mode, now interpreting.

defined class TrafficLight
red: TrafficLight = TrafficLight(red)
yellow: TrafficLight = TrafficLight(yellow)
green: TrafficLight = TrafficLight(green)
TrafficLightEqual: scalaz.Equal[TrafficLight] = scalaz.Equal$$anon$7@42988fee
res3: Boolean = false

Yes と No の型クラス

Scalaz 流に truthy 値の型クラスを作れるか試してみよう。ただし、命名規則は我流でいく。Scalaz は Show、show、show というように 3つや 4つの異なるものに型クラスの名前を使っているため分かりづらい所があると思う。

CanBuildFrom に倣って型クラスは Can で始めて、sjson/sbinary に倣って型クラスのメソッドは動詞 + s と命名するのが僕の好みだ。yesno というのは意味不明なので、truthy と呼ぶ。ゴールは 1.truthy が true を返すことだ。この欠点は型クラスのインスタンスを CanTruthy[Int].truthys(1) のように関数として呼ぶと名前に s が付くことだ。

scala> :paste
// Entering paste mode (ctrl-D to finish)

trait CanTruthy[A] { self =>
  /** @return true, if `a` is truthy. */
  def truthys(a: A): Boolean
}
object CanTruthy {
  def apply[A](implicit ev: CanTruthy[A]): CanTruthy[A] = ev
  def truthys[A](f: A => Boolean): CanTruthy[A] = new CanTruthy[A] {
    def truthys(a: A): Boolean = f(a)
  }
}
trait CanTruthyOps[A] {
  def self: A
  implicit def F: CanTruthy[A]
  final def truthy: Boolean = F.truthys(self)
}
object ToCanIsTruthyOps {
  implicit def toCanIsTruthyOps[A](v: A)(implicit ev: CanTruthy[A]) =
    new CanTruthyOps[A] {
      def self = v
      implicit def F: CanTruthy[A] = ev
    }
}

// Exiting paste mode, now interpreting.

defined trait CanTruthy
defined module CanTruthy
defined trait CanTruthyOps
defined module ToCanIsTruthyOps

scala> import ToCanIsTruthyOps._
import ToCanIsTruthyOps._

Int への型クラスのインスタンスを定義する:

scala> implicit val intCanTruthy: CanTruthy[Int] = CanTruthy.truthys({
         case 0 => false
         case _ => true
       })
intCanTruthy: CanTruthy[Int] = CanTruthy$$anon$1@71780051

scala> 10.truthy
res6: Boolean = true

次が List[A]:

scala> implicit def listCanTruthy[A]: CanTruthy[List[A]] = CanTruthy.truthys({
         case Nil => false
         case _   => true  
       })
listCanTruthy: [A]=> CanTruthy[List[A]]

scala> List("foo").truthy
res7: Boolean = true

scala> Nil.truthy
<console>:23: error: could not find implicit value for parameter ev: CanTruthy[scala.collection.immutable.Nil.type]
              Nil.truthy

またしても不変な型パラメータのせいで Nil を特殊扱いしなくてはいけない。

scala> implicit val nilCanTruthy: CanTruthy[scala.collection.immutable.Nil.type] = CanTruthy.truthys(_ => false)
nilCanTruthy: CanTruthy[collection.immutable.Nil.type] = CanTruthy$$anon$1@1e5f0fd7

scala> Nil.truthy
res8: Boolean = false

Boolean は identity を使える:

scala> implicit val booleanCanTruthy: CanTruthy[Boolean] = CanTruthy.truthys(identity)
booleanCanTruthy: CanTruthy[Boolean] = CanTruthy$$anon$1@334b4cb

scala> false.truthy
res11: Boolean = false

LYAHFGG 同様に CanTruthy 型クラスを使って truthyIf を定義しよう:

では、if の真似をして YesNo 値を取る関数を作ってみましょう。

名前渡しを使って渡された引数の評価を遅延する:

scala> :paste
// Entering paste mode (ctrl-D to finish)

def truthyIf[A: CanTruthy, B, C](cond: A)(ifyes: => B)(ifno: => C) =
  if (cond.truthy) ifyes
  else ifno

// Exiting paste mode, now interpreting.

truthyIf: [A, B, C](cond: A)(ifyes: => B)(ifno: => C)(implicit evidence$1: CanTruthy[A])Any

使用例はこうなる:

scala> truthyIf (Nil) {"YEAH!"} {"NO!"}
res12: Any = NO!

scala> truthyIf (2 :: 3 :: 4 :: Nil) {"YEAH!"} {"NO!"}
res13: Any = YEAH!

scala> truthyIf (true) {"YEAH!"} {"NO!"}
res14: Any = YEAH!

続きはまたあとで。

2日目

昨日はすごいHaskellたのしく学ぼうを頼りに Equal などの Scalaz の型クラスを見てきた。

Functor

LYAHFGG:

今度は、Functor （ファンクター）という型クラスを見ていきたいと思います。Functor は、全体を写せる (map over) ものの型クラスです。

本のとおり、実装がどうなってるかをみてみよう:

trait Functor[F[_]]  { self =>
  /** Lift `f` into `F` and apply to `F[A]`. */
  def map[A, B](fa: F[A])(f: A => B): F[B]

  ...
}

これが可能とする演算子はこうなっている:

trait FunctorOps[F[_],A] extends Ops[F[A]] {
  implicit def F: Functor[F]
  ////
  import Leibniz.===

  final def map[B](f: A => B): F[B] = F.map(self)(f)
  
  ...
}

つまり、これは関数 A => B を受け取り F[B] を返す map メソッドを宣言する。コレクションの map メソッドなら得意なものだ。

scala> List(1, 2, 3) map {_ + 1}
res15: List[Int] = List(2, 3, 4)

Scalaz は Tuple などにも Functor のインスタンスを定義している。

scala> (1, 2, 3) map {_ + 1}
res28: (Int, Int, Int) = (1,2,4)

この演算は Tuple の最後の値のみに適用されていることに注意。詳細は scalaz group での議論を参照。

Functor としての関数

Scalaz は Function1 に対する Functor のインスタンスも定義する。

scala> ((x: Int) => x + 1) map {_ * 7}
res30: Int => Int = <function1>

scala> res30(3)
res31: Int = 28

これは興味深い。つまり、map は関数を合成する方法を与えてくれるが、順番が f compose g とは逆順だ。通りで Scalaz は map のエイリアスとして ∘ を提供するわけだ。Function1 のもう1つのとらえ方は、定義域 (domain) から値域 (range) への無限の写像だと考えることができる。入出力に関しては飛ばして Functors, Applicative Functors and Monoids へ行こう (本だと、「ファンクターからアプリカティブファンクターへ」)。

ファンクターとしての関数 …
ならば、型 fmap :: (a -> b) -> (r -> a) -> (r -> b) が意味するものとは？この型は、a から b への関数と、r から a への関数を引数に受け取り、r から b への関数を返す、と読めます。何か思い出しませんか？そう！関数合成です！

あ、すごい Haskell も僕がさっき言ったように関数合成をしているという結論になったみたいだ。ちょっと待てよ。

ghci> fmap (*3) (+100) 1
303
ghci> (*3) . (+100) $ 1  
303

Haskell では fmap は f compose g を同じ順序で動作してるみたいだ。Scala でも同じ数字を使って確かめてみる:

scala> (((_: Int) * 3) map {_ + 100}) (1)
res40: Int = 103

何かがおかしい。fmap の宣言と Scalaz の map 演算子を比べてみよう:

fmap :: (a -> b) -> f a -> f b

そしてこれが Scalaz:

final def map[B](f: A => B): F[B] = F.map(self)(f)

順番が完全に違っている。ここでの map は F[A] に注入されたメソッドのため、投射される側のデータ構造が最初に来て、次に関数が来る。List で考えると分かりやすい:

ghci> fmap (*3) [1, 2, 3]
[3,6,9]

で

scala> List(1, 2, 3) map {3*}
res41: List[Int] = List(3, 6, 9)

ここでも順番が逆なことが分かる。

fmap も、関数とファンクター値を取ってファンクター値を返す 2 引数関数と思えますが、そうじゃなくて、関数を取って「元の関数に似てるけどファンクター値を取ってファンクター値を返す関数」を返す関数だと思うこともできます。fmap は、関数 a -> b を取って、関数 f a -> f b を返すのです。こういう操作を、関数の持ち上げ (lifting) といいます。

ghci> :t fmap (*2)  
fmap (*2) :: (Num a, Functor f) => f a -> f a  
ghci> :t fmap (replicate 3)  
fmap (replicate 3) :: (Functor f) => f a -> f [a]

この関数の持ち上げ (lifting) は是非やってみたい。Functor の型クラス内に色々便利な関数が定義されていて、その中の 1つに lift がある:

scala> Functor[List].lift {(_: Int) * 2}
res45: List[Int] => List[Int] = <function1>

scala> res45(List(3))
res47: List[Int] = List(6)

Functor は他にもデータ構造の中身を書きかえる >|、as、fpair、strengthL、strengthR、そして void などの演算子を可能とする:

scala> List(1, 2, 3) >| "x"
res47: List[String] = List(x, x, x)

scala> List(1, 2, 3) as "x"
res48: List[String] = List(x, x, x)

scala> List(1, 2, 3).fpair
res49: List[(Int, Int)] = List((1,1), (2,2), (3,3))

scala> List(1, 2, 3).strengthL("x")
res50: List[(String, Int)] = List((x,1), (x,2), (x,3))

scala> List(1, 2, 3).strengthR("x")
res51: List[(Int, String)] = List((1,x), (2,x), (3,x))

scala> List(1, 2, 3).void
res52: List[Unit] = List((), (), ())

Applicative

LYAHFGG:

ここまではファンクター値を写すために、もっぱら 1 引数関数を使ってきました。では、2 引数関数でファンクターを写すと何が起こるでしょう？

scala> List(1, 2, 3, 4) map {(_: Int) * (_:Int)}
<console>:14: error: type mismatch;
 found   : (Int, Int) => Int
 required: Int => ?
              List(1, 2, 3, 4) map {(_: Int) * (_:Int)}
                                             ^

おっと。これはカリー化する必要がある:

scala> List(1, 2, 3, 4) map {(_: Int) * (_:Int)}.curried
res11: List[Int => Int] = List(<function1>, <function1>, <function1>, <function1>)

scala> res11 map {_(9)}
res12: List[Int] = List(9, 18, 27, 36)

LYAHFGG:

Control.Applicative モジュールにある型クラス Applicative に会いに行きましょう！型クラス Applicative は、2つの関数 pure と <*> を定義しています。

Scalaz の Applicative のコントラクトも見てみよう:

trait Applicative[F[_]] extends Apply[F] { self =>
  def point[A](a: => A): F[A]

  /** alias for `point` */
  def pure[A](a: => A): F[A] = point(a)

  ...
}

Applicative は別の型クラス Apply を継承し、それ自身も point とそのエイリアス pure を導入する。

LYAHFGG:

pure は任意の型の引数を受け取り、それをアプリカティブ値の中に入れて返します。 … アプリカティブ値は「箱」というよりも「文脈」と考えるほうが正確かもしれません。pure は、値を引数に取り、その値を何らかのデフォルトの文脈（元の値を再現できるような最小限の文脈）に置くのです。

Scalaz は pure のかわりに point という名前が好きみたいだ。見たところ A の値を受け取り F[A] を返すコンストラクタみたいだ。これは演算子こそは導入しないけど、全てのデータ型に point メソッドとシンボルを使ったエイリアス η を導入する。

scala> 1.point[List]
res14: List[Int] = List(1)

scala> 1.point[Option]
res15: Option[Int] = Some(1)

scala> 1.point[Option] map {_ + 2}
res16: Option[Int] = Some(3)

scala> 1.point[List] map {_ + 2}
res17: List[Int] = List(3)

ちょっとうまく説明できないけど、コンストラクタが抽象化されているのは何か可能性を感じるものがある。

Apply

LYAHFGG:

<*> は fmap の強化版なのです。fmap が普通の関数とファンクター値を引数に取って、関数をファンクター値の中の値に適用してくれるのに対し、<*> は関数の入っているファンクター値と値の入っているファンクター値を引数に取って、1つ目のファンクターの中身である関数を2つ目のファンクターの中身に適用するのです。

trait Apply[F[_]] extends Functor[F] { self =>
  def ap[A,B](fa: => F[A])(f: => F[A => B]): F[B]
}

ap を使って Apply は <*>、*>、<* 演算子を可能とする。

scala>  9.some <*> {(_: Int) + 3}.some
res20: Option[Int] = Some(12)

期待通りだ。

*> と <* は左辺項か右辺項のみ返すバリエーションだ。

scala> 1.some <* 2.some
res35: Option[Int] = Some(1)

scala> none <* 2.some
res36: Option[Nothing] = None

scala> 1.some *> 2.some
res38: Option[Int] = Some(2)

scala> none *> 2.some
res39: Option[Int] = None

Apply としての Option

<*> を使えばいい。

scala> 9.some <*> {(_: Int) + 3}.some
res57: Option[Int] = Some(12)

scala> 3.some <*> { 9.some <*> {(_: Int) + (_: Int)}.curried.some }
res58: Option[Int] = Some(12)

Applicative Style

もう 1つ見つけたのが、コンテナから値だけを抽出して 1つの関数を適用する新記法だ:

scala> ^(3.some, 5.some) {_ + _}
res59: Option[Int] = Some(8)

scala> ^(3.some, none[Int]) {_ + _}
res60: Option[Int] = None

これは 1関数の場合はいちいちコンテナに入れなくてもいいから便利そうだ。これは推測だけど、これのお陰で Scalaz 7 は Applicative そのものでは何も演算子を導入していないんだと思う。実際どうなのかはともかく、Pointed も <$> もいらないみたいだ。

だけど、^(f1, f2) {...} スタイルに問題が無いわけではない。どうやら Function1、Writer、Validation のような 2つの型パラメータを取る Applicative を処理できないようだ。もう 1つ Applicative Builder という Scalaz 6 から使われていたらしい方法がある。 M3 で deprecated になったけど、^(f1, f2) {...} の問題のため、近い将来名誉挽回となるらしい。

こう使う:

scala> (3.some |@| 5.some) {_ + _}
res18: Option[Int] = Some(8)

今の所は |@| スタイルを使おう。

Apply としての List

LYAHFGG:

リスト（正確に言えばリスト型のコンストラクタ []）もアプリカティブファンクターです。意外ですか？

<*> と |@| が使えるかみてみよう:

scala> List(1, 2, 3) <*> List((_: Int) * 0, (_: Int) + 100, (x: Int) => x * x)
res61: List[Int] = List(0, 0, 0, 101, 102, 103, 1, 4, 9)

scala> List(3, 4) <*> { List(1, 2) <*> List({(_: Int) + (_: Int)}.curried, {(_: Int) * (_: Int)}.curried) }
res62: List[Int] = List(4, 5, 5, 6, 3, 4, 6, 8)

scala> (List("ha", "heh", "hmm") |@| List("?", "!", ".")) {_ + _}
res63: List[String] = List(ha?, ha!, ha., heh?, heh!, heh., hmm?, hmm!, hmm.)

Zip List

LYAHFGG:

ところが、[(+3),(*2)] <*> [1,2] の挙動は、左辺の1つ目の関数を右辺の1つ目の値に適用し、左辺の2つ目の関数を右辺の2つ目の値に適用する、というのではまずいのでしょうか？それなら結果は [4,4] になるはずです。これは [1 + 3, 2 * 2] と考えることもできます。

これは Scalaz で書けるけど、簡単ではない。

scala> streamZipApplicative.ap(Tags.Zip(Stream(1, 2))) (Tags.Zip(Stream({(_: Int) + 3}, {(_: Int) * 2})))
res32: scala.collection.immutable.Stream[Int] with Object{type Tag = scalaz.Tags.Zip} = Stream(4, ?)

scala> res32.toList
res33: List[Int] = List(4, 4)

Tagged type を使った例は明日また詳しく説明する。

Applicative の便利な関数

LYAHFGG:

Control.Applicative には liftA2 という、以下のような型を持つ関数があります。

liftA2 :: (Applicative f) => (a -> b -> c) -> f a -> f b -> f c .

Apply[F].lift2 というものがある:

scala> Apply[Option].lift2((_: Int) :: (_: List[Int]))
res66: (Option[Int], Option[List[Int]]) => Option[List[Int]] = <function2>

scala> res66(3.some, List(4).some)
res67: Option[List[Int]] = Some(List(3, 4))

LYAHFGG:

では、「アプリカティブ値のリスト」を取って「リストを返り値として持つ1つのアプリカティブ値」を返す関数を実装してみましょう。これを sequenceA と呼ぶことにします。

sequenceA :: (Applicative f) => [f a] -> f [a]  
sequenceA [] = pure []  
sequenceA (x:xs) = (:) <$> x <*> sequenceA xs

これを Scalaz でも実装できるか試してみよう!

scala> def sequenceA[F[_]: Applicative, A](list: List[F[A]]): F[List[A]] = list match {
         case Nil     => (Nil: List[A]).point[F]
         case x :: xs => (x |@| sequenceA(xs)) {_ :: _} 
       }
sequenceA: [F[_], A](list: List[F[A]])(implicit evidence$1: scalaz.Applicative[F])F[List[A]]

テストしてみよう:

scala> sequenceA(List(1.some, 2.some))
res82: Option[List[Int]] = Some(List(1, 2))

scala> sequenceA(List(3.some, none, 1.some))
res85: Option[List[Int]] = None

scala> sequenceA(List(List(1, 2, 3), List(4, 5, 6)))
res86: List[List[Int]] = List(List(1, 4), List(1, 5), List(1, 6), List(2, 4), List(2, 5), List(2, 6), List(3, 4), List(3, 5), List(3, 6))

正しい答えが得られた。興味深いのは結局 Pointed が必要になったことと、sequenceA が型クラスに関してジェネリックなことだ。

Function1 の片側が Int に固定された例は、残念ながら黒魔術を召喚する必要がある。

scala> type Function1Int[A] = ({type l[A]=Function1[Int, A]})#l[A]
defined type alias Function1Int

scala> sequenceA(List((_: Int) + 3, (_: Int) + 2, (_: Int) + 1): List[Function1Int[Int]])
res1: Int => List[Int] = <function1>

scala> res1(3)
res2: List[Int] = List(6, 5, 4)

結構長くなったけど、ここまでたどり着けて良かったと思う。続きはまたあとで。

3日目

昨日は map 演算子を加える Functor から始めて、Pointed[F].point や Applicative な ^(f1, f2) {_ :: _} 構文を使った多態的な関数 sequenceA にたどり着いた。

型を司るもの、カインド

型や型クラスを自分で作ろうの節で昨日のうちにカバーしておくべきだったけどしなかったのはカインドと型の話だ。Scalaz の理解には関係無いだろうと思ってたけど、関係あるので、座って聞いて欲しい。

すごいHaskellたのしく学ぼう曰く:

型とは、値について何らかの推論をするために付いている小さなラベルです。そして、型にも小さなラベルが付いているんです。その名は種類 (kind)。 … 種類とはそもそも何者で、何の役に立つのでしょう？さっそく GHCi の :k コマンドを使って、型の種類を調べてみましょう。

Scala 2.10 時点では Scala REPL に :k コマンドが無かったので、ひとつ書いてみた: kind.scala。 scala/scala#2340 を送ってくれた George Leontiev さん (@folone) その他の協力もあって、Scala 2.11 より :kind コマンドは標準機能として取り込まれた。使ってみよう:

scala> :k Int
scala.Int's kind is A

scala> :k -v Int
scala.Int's kind is A
*
プロパーな型だ。

scala> :k -v Option
scala.Option's kind is F[+A]
* -(+)-> *
型コンストラクタ: 1階カインド型だ。

scala> :k -v Either
scala.util.Either's kind is F[+A1,+A2]
* -(+)-> * -(+)-> *
型コンストラクタ: 1階カインド型だ。

scala> :k -v Equal
scalaz.Equal's kind is F[A]
* -> *
型コンストラクタ: 1階カインド型だ。

scala> :k -v Functor
scalaz.Functor's kind is X[F[A]]
(* -> *) -> *
型コンストラクタを受け取る型コンストラクタ: 高カインド型だ。

上から順番に。Int と他の全ての値を作ることのできる型はプロパーな型と呼ばれ * というシンボルで表記される (「型」と読む)。これは値レベルだと 1 に相当する。Scala の型変数構文を用いるとこれは A と書ける。

1階値、つまり (_: Int) + 3 のような値コンストラクタ、は普通関数と呼ばれる。同様に、1階カインド型はプロパーな型になるために他の型を受け取る型のことだ。これは普通型コンストラクタと呼ばれる。Option、Either、Equal などは全て1階カインドだ。これらが他の型を受け取ることを表記するのにカリー化した表記法を用いて * -> * や * -> * -> * などと書く。このとき Option[Int] は * で、Option が * -> * であることに注意。Scala の型変数構文を用いるとこれらは F[+A]、 F[+A1,+A2] となる。

(f: Int => Int, list: List[Int]) => list map {f} のような高階値、つまり関数を受け取る関数、は普通高階関数と呼ばれる。同様に、高カインド型は型コンストラクタを受け取る型コンストラクタだ。これは多分高カインド型コンストラクタと呼ばれるべきだが、その名前は使われていない。これらは (* -> *) -> * と表記される。Scala の型変数構文を用いるとこれは X[F[A]] と書ける。

Scalaz 7.1 の場合、Equal その他は F[A] のカインドを持ち、Functor とその派生型は X[F[A]]カインドを持つ。 Scala は型クラスという概念を型コンストラクタを用いてエンコード (悪く言うとコンプレクト) するため、この辺の用語が混乱しやすいことがある。例えば、データ構造である List は函手 (functor) となるという言い方をして、これは List に対して Functor[List] のインスタンスを導き出せるという意味だ。List に対するインスタンスなんて一つしか無いのが分かってるので、「List は函手である (List is a functor)」と言うことができる。 is-a に関する議論は以下も参照:

In FP, "is-a" means "an instance can be derived from." @jimduey #CPL14 It's a provable relationship, not reliant on LSP.
— Jessica Kerr (@jessitron) February 25, 2014

List そのものは F[+A] なので、F が函手に関連すると覚えるのは簡単だ。しかし、型クラス定義の Functor は F[A] を囲む必要があるので、カインドは X[F[A]] となっている。さらにこれを混乱させるのが、Scala から型コンストラクタを第一級変数として扱えることが目新しかったため、コンパイラは 1階カインド型でも「高カインド型」と呼んでいることだ:

scala> trait Test {
         type F[_]
       }
<console>:14: warning: higher-kinded type should be enabled
by making the implicit value scala.language.higherKinds visible.
This can be achieved by adding the import clause 'import scala.language.higherKinds'
or by setting the compiler option -language:higherKinds.
See the Scala docs for value scala.language.higherKinds for a discussion
why the feature should be explicitly enabled.
         type F[_]
              ^

注入された演算子を使っているぶんにはこれらの心配をする必要はないはずだ:

scala> List(1, 2, 3).shows
res11: String = [1,2,3]

だけど Show[A].shows を使いたければ、これが Show[List[Int]] であって Show[List] ではないことを理解している必要がある。同様に、関数を持ち上げ (lift) たければ Functor[F] (F は Functor の F) だと知っている必要がある:

scala> Functor[List[Int]].lift((_: Int) + 2)
<console>:14: error: List[Int] takes no type parameters, expected: one
              Functor[List[Int]].lift((_: Int) + 2)
                      ^

scala> Functor[List].lift((_: Int) + 2)
res13: List[Int] => List[Int] = <function1>

チートシートを始めたとき、Scalaz 7 のソースコードに合わせて Equal[F] と書いた。すると Adam Rosien さんに Equal[A] と表記すべきと指摘された。

@eed3si9n love the scalaz cheat sheet start, but using the type param F usually means Functor, what about A instead?
— Adam Rosien (@arosien) September 1, 2012

これで理由がよく分かった!

Tagged type

「すごいHaskellたのしく学ぼう」の本を持ってるひとは新しい章に進める。モノイドだ。ウェブサイトを読んでるひとは Functors, Applicative Functors and Monoids の続きだ。

LYAHFGG:

Haskell の newtype キーワードは、まさにこのような「1つの型を取り、それを何かにくるんで別の型に見せかけたい」という場合のために作られたものです。

これは Haskell の言語レベルでの機能なので、Scala に移植するのは無理なんじゃないかと思うと思う。ところが、約1年前 (2011年9月) Miles Sabin さん (@milessabin) が gist を書き、それを Tagged と名付け、Jason Zaugg さん (@retronym) が @@ という型エイリアスを加えた。

type Tagged[U] = { type Tag = U }
type @@[T, U] = T with Tagged[U]

これについて読んでみたいひとは Eric Torreborre さん (@etorreborre) が Practical uses for Unboxed Tagged Types、それから Tim Perrett さん (@timperrett) が Unboxed new types within Scalaz7 を書いている。

例えば、体積をキログラムで表現したいとする。kg は国際的な標準単位だからだ。普通は Double を渡して終わる話だけど、それだと他の Double の値と区別が付かない。case class は使えるだろうか?

case class KiloGram(value: Double)

型安全性は加わったけど、使うたびに x.value というふうに値を取り出さなきゃいけないのが不便だ。Tagged type 登場。

scala> sealed trait KiloGram
defined trait KiloGram

scala> def KiloGram[A](a: A): A @@ KiloGram = Tag[A, KiloGram](a)
KiloGram: [A](a: A)scalaz.@@[A,KiloGram]

scala> val mass = KiloGram(20.0)
mass: scalaz.@@[Double,KiloGram] = 20.0

scala> 2 * Tag.unwrap(mass) // this doesn't work on REPL
res2: Double = 40.0

scala> 2 * Tag.unwrap(mass)
<console>:17: error: wrong number of type parameters for method unwrap$mDc$sp: [T](a: Object{type Tag = T; type Self = Double})Double
              2 * Tag.unwrap(mass)
                      ^

scala> 2 * scalaz.Tag.unsubst[Double, Id, KiloGram](mass)
res2: Double = 40.0

以前は 2 * mass と書けたけども Scalaz 7.1 以降は明示的にタグを unwrap しなければいけなくなった。さらに REPL のバグ SI-8871 のせいで、Tag.unwrap が動作しないため、Tag.unsubst を使う必要があった。補足しておくと、A @@ KiloGram は scalaz.@@[A, KiloGram] の中置記法だ。これで相対論的エネルギーを計算する関数を定義できる。

scala> sealed trait JoulePerKiloGram
defined trait JoulePerKiloGram

scala> def JoulePerKiloGram[A](a: A): A @@ JoulePerKiloGram = Tag[A, JoulePerKiloGram](a)
JoulePerKiloGram: [A](a: A)scalaz.@@[A,JoulePerKiloGram]

scala> def energyR(m: Double @@ KiloGram): Double @@ JoulePerKiloGram =
         JoulePerKiloGram(299792458.0 * 299792458.0 * Tag.unsubst[Double, Id, KiloGram](m))
energyR: (m: scalaz.@@[Double,KiloGram])scalaz.@@[Double,JoulePerKiloGram]

scala> energyR(mass)
res4: scalaz.@@[Double,JoulePerKiloGram] = 1.79751035747363533E18

scala> energyR(10.0)
<console>:18: error: type mismatch;
 found   : Double(10.0)
 required: scalaz.@@[Double,KiloGram]
    (which expands to)  AnyRef{type Tag = KiloGram; type Self = Double}
              energyR(10.0)
                      ^

見ての通り、素の Double を energyR に渡すとコンパイル時に失敗する。これは newtype そっくりだけど、Int @@ KiloGram など定義できるからより強力だと言える。

Monoid について

LYAHFGG:

どうやら、* に 1 という組み合わせと、++ に [] という組み合わせは、共通の性質を持っているようですね。
関数は引数を2つ取る。
2つの引数および返り値の型はすべて等しい。
2引数関数を施して相手を変えないような特殊な値が存在する。

これを Scala で確かめてみる:

scala> 4 * 1
res16: Int = 4

scala> 1 * 9
res17: Int = 9

scala> List(1, 2, 3) ++ Nil
res18: List[Int] = List(1, 2, 3)

scala> Nil ++ List(0.5, 2.5)
res19: List[Double] = List(0.5, 2.5)

あってるみたいだ。

LYAHFGG:

例えば、(3 * 4) * 5 も 3 * (4 * 5) も、答は 60 です。++ についてもこの性質は成り立ちます。 … この性質を結合的 (associativity) と呼びます。演算 * と ++ は結合的であると言います。結合的でない演算の例は - です。

これも確かめよう:

scala> (3 * 2) * (8 * 5) assert_=== 3 * (2 * (8 * 5))

scala> List("la") ++ (List("di") ++ List("da")) assert_=== (List("la") ++ List("di")) ++ List("da")

エラーがないから等価ということだ。これを monoid と言うらしい。

Monoid

LYAHFGG:

モノイドは、結合的な二項演算子（2引数関数）と、その演算に関する単位元からなる構造です。

Scalaz の Monoid の型クラスのコントラクトを見てみよう:

trait Monoid[A] extends Semigroup[A] { self =>
  ////
  /** The identity element for `append`. */
  def zero: A
  
  ...
}

Semigroup

Monoid は Semigroup を継承するみたいなのでその型クラスも見てみる。

trait Semigroup[A]  { self =>
  def append(a1: A, a2: => A): A
  ...
}

これが演算子だ:

trait SemigroupOps[A] extends Ops[A] {
  final def |+|(other: => A): A = A.append(self, other)
  final def mappend(other: => A): A = A.append(self, other)
  final def ⊹(other: => A): A = A.append(self, other)
}

mappend 演算子とシンボルを使ったエイリアス |+| と ⊹ を導入する。

LYAHFGG:

次は mappend です。これは、お察しのとおり、モノイド固有の二項演算です。mappend は同じ型の引数を2つ取り、その型の別の値を返します。

すごい Haskell は名前が mappend だからといって、* の場合のように必ずしも何かを追加 (append) してるわけじゃないと注意している。これを使ってみよう:

scala> List(1, 2, 3) mappend List(4, 5, 6)
res23: List[Int] = List(1, 2, 3, 4, 5, 6)

scala> "one" mappend "two"
res25: String = onetwo

|+| を使うのが Scalaz では一般的みたいだ:

scala> List(1, 2, 3) |+| List(4, 5, 6)
res26: List[Int] = List(1, 2, 3, 4, 5, 6)

scala> "one" |+| "two"
res27: String = onetwo

より簡潔にみえる。

Monoid に戻る

trait Monoid[A] extends Semigroup[A] { self =>
  ////
  /** The identity element for `append`. */
  def zero: A
  
  ...
}

LYAHFGG:

mempty は、そのモノイドの単位元を表わします。

これは Scalaz では zero と呼ばれている。

scala> Monoid[List[Int]].zero
res15: List[Int] = List()

scala> Monoid[String].zero
res16: String = ""

Tags.Multiplication

LYAHFGG:

さて、数をモノイドにする2つの方法は、どちらも素晴らしく優劣つけがたいように思えます。一体どちらを選べまよいのでしょう？実は、1つだけ選ぶ必要はないのです。

これが Scalaz 7.1 での Tagged type の出番だ。最初から定義済みのタグは Tags にある。8つのタグが Monoid 用で、1つ Zip という名前のタグが Applicative 用にある。(もしかしてこれが昨日見つけられなかった Zip List?)

scala> Tags.Multiplication(10) |+| Monoid[Int @@ Tags.Multiplication].zero
res21: scalaz.@@[Int,scalaz.Tags.Multiplication] = 10

よし! |+| を使って数字を掛けることができた。加算には普通の Int を使う。

scala> 10 |+| Monoid[Int].zero
res22: Int = 10

Tags.Disjunction and Tags.Conjunction

LYAHFGG:

モノイドにする方法が2通りあって、どちらも捨てがたいような型は、Num a 以外にもあります。Bool です。1つ目の方法は || をモノイド演算とし、False を単位元とする方法です。 … Bool を Monoid のインスタンスにするもう1つの方法は、Any のいわば真逆です。&& をモノイド演算とし、True を単位元とする方法です。

Scalaz 7 でこれらはそれぞれ Boolean @@ Tags.Disjunction、Boolean @@ Tags.Conjunction と呼ばれている。

scala> Tags.Disjunction(true) |+| Tags.Disjunction(false)
res28: scalaz.@@[Boolean,scalaz.Tags.Disjunction] = true

scala> Monoid[Boolean @@ Tags.Disjunction].zero |+| Tags.Disjunction(true)
res29: scalaz.@@[Boolean,scalaz.Tags.Disjunction] = true

scala> Monoid[Boolean @@ Tags.Disjunction].zero |+| Monoid[Boolean @@ Tags.Disjunction].zero
res30: scalaz.@@[Boolean,scalaz.Tags.Disjunction] = false

scala> Monoid[Boolean @@ Tags.Conjunction].zero |+| Tags.Conjunction(true)
res31: scalaz.@@[Boolean,scalaz.Tags.Conjunction] = true

scala> Monoid[Boolean @@ Tags.Conjunction].zero |+| Tags.Conjunction(false)
res32: scalaz.@@[Boolean,scalaz.Tags.Conjunction] = false

Monoid としての Ordering

LYAHFGG:

Ordering の場合、モノイドを見抜くのはちょっと難しいです。しかし Ordering の Monoid インスタンスは、分かってみれば今までのモノイドと同じくごく自然な定義で、しかも便利なんです。

ちょっと変わっているが、確かめてみよう。

scala> Ordering.LT |+| Ordering.GT
<console>:14: error: value |+| is not a member of object scalaz.Ordering.LT
              Ordering.LT |+| Ordering.GT
                          ^

scala> (Ordering.LT: Ordering) |+| (Ordering.GT: Ordering)
res42: scalaz.Ordering = LT

scala> (Ordering.GT: Ordering) |+| (Ordering.LT: Ordering)
res43: scalaz.Ordering = GT

scala> Monoid[Ordering].zero |+| (Ordering.LT: Ordering)
res44: scalaz.Ordering = LT

scala> Monoid[Ordering].zero |+| (Ordering.GT: Ordering)
res45: scalaz.Ordering = GT

LYAHFGG:

では、このモノイドはどういうときに便利なのでしょう？例えば、2つの文字列を引数に取り、その長さを比較して　Ordering を返す関数を書きたいとしましょう。だたし、2つの文字列の長さが等しいときは、直ちに EQ を返すのではなくて、2つの文字列の辞書順比較することとします。

Ordering.EQ 以外の場合は左辺の比較が保存されるため、これを使って2つのレベルの比較を合成することができる。Scalaz を使って lengthCompare を実装してみよう:

scala> def lengthCompare(lhs: String, rhs: String): Ordering =
         (lhs.length ?|? rhs.length) |+| (lhs ?|? rhs)
lengthCompare: (lhs: String, rhs: String)scalaz.Ordering

scala> lengthCompare("zen", "ants")
res46: scalaz.Ordering = LT

scala> lengthCompare("zen", "ant")
res47: scalaz.Ordering = GT

合ってる。“zen” は “ants” より短いため LT が返ってきた。

他にも Monoid があるけど、今日はこれでおしまいにしよう。また後でここから続ける。

4日目

昨日は、カインドと型について考え、Tagged type を探検して、さまざまな型の 2項演算を抽象化する方法としての Semigroup と Monoid をみてみた。

Jason Zaugg にもコメントをもらった:

This might be a good point to pause and discuss the laws by which a well behaved type class instance must abide.

この辺りで一度立ち止まって、行儀の良い型クラスが従うべき法則についても議論すべきじゃないですか。

すごいHaskellたのしく学ぼうの型クラスの法則に関しては全て飛ばしてきたところを、パトカーに止められた形だ。恥ずかしい限りだ。

Functor則

LYAHFGG:

すべてのファンクターの性質や挙動は、ある一定の法則に従うことになっています。 … ファンクターの第一法則は、「id でファンクター値を写した場合、ファンクター値が変化してはいけない」というものです。

言い換えると、

scala> List(1, 2, 3) map {identity} assert_=== List(1, 2, 3)

第二法則は、2つの関数 f と g について、「f と g の合成関数でファンクター値を写したもの」と、「まず g、次に f でファンクター値を写したもの」が等しいことを要求します。

言い換えると、

scala> (List(1, 2, 3) map {{(_: Int) * 3} map {(_: Int) + 1}}) assert_=== (List(1, 2, 3) map {(_: Int) * 3} map {(_: Int) + 1})

これらの法則は Functor の実装者が従うべき法則で、コンパイラはチェックしてくれない。Scalaz 7 にはコードでこれを記述した FunctorLaw trait が入っている:

trait FunctorLaw {
  /** The identity function, lifted, is a no-op. */
  def identity[A](fa: F[A])(implicit FA: Equal[F[A]]): Boolean = FA.equal(map(fa)(x => x), fa)

  /**
   * A series of maps may be freely rewritten as a single map on a
   * composed function.
   */
  def associative[A, B, C](fa: F[A], f1: A => B, f2: B => C)(implicit FC: Equal[F[C]]): Boolean = FC.equal(map(map(fa)(f1))(f2), map(fa)(f2 compose f1))
}

それだけじゃなく、これらを任意の値でテストする ScalaCheck へのバインディングもついてきてる。以下が REPL からこれを実行するための build.sbt だ:

scalaVersion := "2.11.2"

val scalazVersion = "7.1.0"

libraryDependencies ++= Seq(
  "org.scalaz" %% "scalaz-core" % scalazVersion,
  "org.scalaz" %% "scalaz-effect" % scalazVersion,
  "org.scalaz" %% "scalaz-typelevel" % scalazVersion,
  "org.scalaz" %% "scalaz-scalacheck-binding" % scalazVersion % "test"
)

scalacOptions += "-feature"

initialCommands in console := "import scalaz._, Scalaz._"

initialCommands in console in Test := "import scalaz._, Scalaz._, scalacheck.ScalazProperties._, scalacheck.ScalazArbitrary._,scalacheck.ScalaCheckBinding._"

通常の sbt console のかわりに、sbt test:console を実行する:

$ sbt test:console
[info] Starting scala interpreter...
[info] 
import scalaz._
import Scalaz._
import scalacheck.ScalazProperties._
import scalacheck.ScalazArbitrary._
import scalacheck.ScalaCheckBinding._
Welcome to Scala version 2.10.3 (Java HotSpot(TM) 64-Bit Server VM, Java 1.6.0_45).
Type in expressions to have them evaluated.
Type :help for more information.

scala>

List が Functor則を満たすかテストしてる:

scala> functor.laws[List].check
+ functor.identity: OK, passed 100 tests.
+ functor.associative: OK, passed 100 tests.

法則を破る

本にあわせて、法則を破ってみよう:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait COption[+A] {}
case class CSome[A](counter: Int, a: A) extends COption[A]
case object CNone extends COption[Nothing]

implicit def coptionEqual[A]: Equal[COption[A]] = Equal.equalA
implicit val coptionFunctor = new Functor[COption] {
  def map[A, B](fa: COption[A])(f: A => B): COption[B] = fa match {
    case CNone => CNone
    case CSome(c, a) => CSome(c + 1, f(a))
  }
}

// Exiting paste mode, now interpreting.

defined trait COption
defined class CSome
defined module CNone
coptionEqual: [A]=> scalaz.Equal[COption[A]]
coptionFunctor: scalaz.Functor[COption] = $anon$1@42538425

scala> (CSome(0, "ho"): COption[String]) map {(_: String) + "ha"}
res4: COption[String] = CSome(1,hoha)

scala> (CSome(0, "ho"): COption[String]) map {identity}
res5: COption[String] = CSome(1,ho)

これは最初の法則を破っている。検知できるかみてみよう。

scala> functor.laws[COption].check
<console>:26: error: could not find implicit value for parameter af: org.scalacheck.Arbitrary[COption[Int]]
              functor.laws[COption].check
                          ^

COption[A] の「任意」の値を暗黙に提供しなきゃいけないみたいだ:

scala> import org.scalacheck.{Gen, Arbitrary}
import org.scalacheck.{Gen, Arbitrary}

scala> implicit def COptionArbiterary[A](implicit a: Arbitrary[A]): Arbitrary[COption[A]] =
         a map { a => (CSome(0, a): COption[A]) }
COptionArbiterary: [A](implicit a: org.scalacheck.Arbitrary[A])org.scalacheck.Arbitrary[COption[A]]

これは面白い。ScalaCheck そのものは map メソッドを提供しないけど、Scalaz が Functor[Arbitrary] として注入している! あまりぱっとしない任意の COption だけど、ScalaCheck をよく知らないのでこれでいいとする。

scala> functor.laws[COption].check
! functor.identity: Falsified after 0 passed tests.
> ARG_0: CSome(0,-170856004)
! functor.associative: Falsified after 0 passed tests.
> ARG_0: CSome(0,1)
> ARG_1: <function1>
> ARG_2: <function1>

期待通りテストは失敗した。

Applicative則

これが Applicative則だ:

  trait ApplicativeLaw extends FunctorLaw {
    def identityAp[A](fa: F[A])(implicit FA: Equal[F[A]]): Boolean =
      FA.equal(ap(fa)(point((a: A) => a)), fa)

    def composition[A, B, C](fbc: F[B => C], fab: F[A => B], fa: F[A])(implicit FC: Equal[F[C]]) =
      FC.equal(ap(ap(fa)(fab))(fbc), ap(fa)(ap(fab)(ap(fbc)(point((bc: B => C) => (ab: A => B) => bc compose ab)))))

    def homomorphism[A, B](ab: A => B, a: A)(implicit FB: Equal[F[B]]): Boolean =
      FB.equal(ap(point(a))(point(ab)), point(ab(a)))

    def interchange[A, B](f: F[A => B], a: A)(implicit FB: Equal[F[B]]): Boolean =
      FB.equal(ap(point(a))(f), ap(f)(point((f: A => B) => f(a))))
  }

LYAHFGG も詳細は飛ばしているので、僕も見逃してもらう。

Semigroup則

これが、Semigroup則だ:

  /**
   * A semigroup in type F must satisfy two laws:
    *
    *  - '''closure''': `∀ a, b in F, append(a, b)` is also in `F`. This is enforced by the type system.
    *  - '''associativity''': `∀ a, b, c` in `F`, the equation `append(append(a, b), c) = append(a, append(b , c))` holds.
   */
  trait SemigroupLaw {
    def associative(f1: F, f2: F, f3: F)(implicit F: Equal[F]): Boolean =
      F.equal(append(f1, append(f2, f3)), append(append(f1, f2), f3))
  }

1 * (2 * 3) と (1 * 2) * 3 が満たされるべきで、これは結合律 (associative) と呼ばれるのは覚えているよね。

scala> semigroup.laws[Int @@ Tags.Multiplication].check
+ semigroup.associative: OK, passed 100 tests.

Monoid則

これが Monoid則だ:

  /**
   * Monoid instances must satisfy [[scalaz.Semigroup.SemigroupLaw]] and 2 additional laws:
   *
   *  - '''left identity''': `forall a. append(zero, a) == a`
   *  - '''right identity''' : `forall a. append(a, zero) == a`
   */
  trait MonoidLaw extends SemigroupLaw {
    def leftIdentity(a: F)(implicit F: Equal[F]) = F.equal(a, append(zero, a))
    def rightIdentity(a: F)(implicit F: Equal[F]) = F.equal(a, append(a, zero))
  }

この法則は簡単だ。単位元 (identity value) を左右のどちらに |+| (mappend) しても同じ値が返ってくるということだ。乗算で確認:

scala> 1 * 2 assert_=== 2

scala> 2 * 1 assert_=== 2

Scalaz で書くと:

scala> (Monoid[Int @@ Tags.Multiplication].zero |+| Tags.Multiplication(2): Int) assert_=== 2

scala> (Tags.Multiplication(2) |+| Monoid[Int @@ Tags.Multiplication].zero: Int) assert_=== 2

scala> monoid.laws[Int @@ Tags.Multiplication].check
+ monoid.semigroup.associative: OK, passed 100 tests.
+ monoid.left identity: OK, passed 100 tests.
+ monoid.right identity: OK, passed 100 tests.

Monoid としての Option

LYAHFGG:

Maybe a をモノイドにする1つ目の方法は、型引数 a がモノイドであるときに限り Maybe a もモノイドであるとし、Maybe a の mappend を、Just の中身の mappend を使って定義することです。

Scalaz がこうなっているか確認しよう。std/Option.scala 参照:

  implicit def optionMonoid[A: Semigroup]: Monoid[Option[A]] = new Monoid[Option[A]] {
    def append(f1: Option[A], f2: => Option[A]) = (f1, f2) match {
      case (Some(a1), Some(a2)) => Some(Semigroup[A].append(a1, a2))
      case (Some(a1), None)     => f1
      case (None, Some(a2))     => f2
      case (None, None)         => None
    }

    def zero: Option[A] = None
  }

実装はシンプルで良い感じだ。Context bound の A: Semigroup は A が |+| をサポートしなければいけないと言っている。残りはパターンマッチングだ。本の言うとおりの振る舞いだ。

scala> (none: Option[String]) |+| "andy".some
res23: Option[String] = Some(andy)

scala> (Ordering.LT: Ordering).some |+| none
res25: Option[scalaz.Ordering] = Some(LT)

ちゃんと動く。

LYAHFGG:

中身がモノイドがどうか分からない状態では、mappend は使えません。どうすればいいでしょう？ 1つの選択は、第一引数を返して第二引数は捨てる、と決めておくことです。この用途のために First a というものが存在します。

Haskell は newtype を使って First 型コンストラクタを実装している。Scalaz 7 は強力な Tagged type を使っている:

scala> Tags.First('a'.some) |+| Tags.First('b'.some)
res26: scalaz.@@[Option[Char],scalaz.Tags.First] = Some(a)

scala> Tags.First(none: Option[Char]) |+| Tags.First('b'.some)
res27: scalaz.@@[Option[Char],scalaz.Tags.First] = Some(b)

scala> Tags.First('a'.some) |+| Tags.First(none: Option[Char])
res28: scalaz.@@[Option[Char],scalaz.Tags.First] = Some(a)

LYAHFGG:

逆に、2つの Just を mappend したときに後のほうの引数を優先するような Maybe a が欲しい、という人のために、Data.Monoid には Last a 型も用意されています。

これは Tags.Last だ:

scala> Tags.Last('a'.some) |+| Tags.Last('b'.some)
res29: scalaz.@@[Option[Char],scalaz.Tags.Last] = Some(b)

scala> Tags.Last(none: Option[Char]) |+| Tags.Last('b'.some)
res30: scalaz.@@[Option[Char],scalaz.Tags.Last] = Some(b)

scala> Tags.Last('a'.some) |+| Tags.Last(none: Option[Char])
res31: scalaz.@@[Option[Char],scalaz.Tags.Last] = Some(a)

Foldable

LYAHFGG:

畳み込み相性の良いデータ構造は実にたくさんあるので、Foldable 型クラスが導入されました。Functor が関数で写せるものを表すように、Foldable は畳み込みできるものを表しています。

Scalaz でこれに対応するものも Foldable と呼ばれている。型クラスのコントラクトも見てみよう:

trait Foldable[F[_]] { self =>
  /** Map each element of the structure to a [[scalaz.Monoid]], and combine the results. */
  def foldMap[A,B](fa: F[A])(f: A => B)(implicit F: Monoid[B]): B

  /**Right-associative fold of a structure. */
  def foldRight[A, B](fa: F[A], z: => B)(f: (A, => B) => B): B

  ...
}

演算子はこれだ:

/** Wraps a value `self` and provides methods related to `Foldable` */
trait FoldableOps[F[_],A] extends Ops[F[A]] {
  implicit def F: Foldable[F]
  ////
  final def foldMap[B: Monoid](f: A => B = (a: A) => a): B = F.foldMap(self)(f)
  final def foldRight[B](z: => B)(f: (A, => B) => B): B = F.foldRight(self, z)(f)
  final def foldLeft[B](z: B)(f: (B, A) => B): B = F.foldLeft(self, z)(f)
  final def foldRightM[G[_], B](z: => B)(f: (A, => B) => G[B])(implicit M: Monad[G]): G[B] = F.foldRightM(self, z)(f)
  final def foldLeftM[G[_], B](z: B)(f: (B, A) => G[B])(implicit M: Monad[G]): G[B] = F.foldLeftM(self, z)(f)
  final def foldr[B](z: => B)(f: A => (=> B) => B): B = F.foldr(self, z)(f)
  final def foldl[B](z: B)(f: B => A => B): B = F.foldl(self, z)(f)
  final def foldrM[G[_], B](z: => B)(f: A => ( => B) => G[B])(implicit M: Monad[G]): G[B] = F.foldrM(self, z)(f)
  final def foldlM[G[_], B](z: B)(f: B => A => G[B])(implicit M: Monad[G]): G[B] = F.foldlM(self, z)(f)
  final def foldr1(f: (A, => A) => A): Option[A] = F.foldr1(self)(f)
  final def foldl1(f: (A, A) => A): Option[A] = F.foldl1(self)(f)
  final def sumr(implicit A: Monoid[A]): A = F.foldRight(self, A.zero)(A.append)
  final def suml(implicit A: Monoid[A]): A = F.foldLeft(self, A.zero)(A.append(_, _))
  final def toList: List[A] = F.toList(self)
  final def toIndexedSeq: IndexedSeq[A] = F.toIndexedSeq(self)
  final def toSet: Set[A] = F.toSet(self)
  final def toStream: Stream[A] = F.toStream(self)
  final def all(p: A => Boolean): Boolean = F.all(self)(p)
  final def ∀(p: A => Boolean): Boolean = F.all(self)(p)
  final def allM[G[_]: Monad](p: A => G[Boolean]): G[Boolean] = F.allM(self)(p)
  final def anyM[G[_]: Monad](p: A => G[Boolean]): G[Boolean] = F.anyM(self)(p)
  final def any(p: A => Boolean): Boolean = F.any(self)(p)
  final def ∃(p: A => Boolean): Boolean = F.any(self)(p)
  final def count: Int = F.count(self)
  final def maximum(implicit A: Order[A]): Option[A] = F.maximum(self)
  final def minimum(implicit A: Order[A]): Option[A] = F.minimum(self)
  final def longDigits(implicit d: A <:< Digit): Long = F.longDigits(self)
  final def empty: Boolean = F.empty(self)
  final def element(a: A)(implicit A: Equal[A]): Boolean = F.element(self, a)
  final def splitWith(p: A => Boolean): List[List[A]] = F.splitWith(self)(p)
  final def selectSplit(p: A => Boolean): List[List[A]] = F.selectSplit(self)(p)
  final def collapse[X[_]](implicit A: ApplicativePlus[X]): X[A] = F.collapse(self)
  final def concatenate(implicit A: Monoid[A]): A = F.fold(self)
  final def traverse_[M[_]:Applicative](f: A => M[Unit]): M[Unit] = F.traverse_(self)(f)

  ////
}

これはスゴい。コレクションライブラリさながらだけど、Order などの型クラスを駆使している。畳込みをやってみよう:

scala> List(1, 2, 3).foldRight (1) {_ * _}
res49: Int = 6

scala> 9.some.foldLeft(2) {_ + _}
res50: Int = 11

これらは標準ライブラリにも入っている。foldMap 演算子も試してみよう。Monoid[A] が zero と |+| を提供するから、畳込みに十分な情報がある。Foldable がいつも Monoid を持っているとは限らないので、[B: Monoid] である A => B 関数が必要だ:

scala> List(1, 2, 3) foldMap {identity}
res53: Int = 6

scala> List(true, false, true, true) foldMap {Tags.Disjunction.apply}
res56: scalaz.@@[Boolean,scalaz.Tags.Disjunction] = true

Tags.Disjunction(true) と一つ一つ書きだして |+| でつなぐよりずっと楽だ。

続きはまた後で。今週は出張なので、ちょっとペースは落ちるかも。

5日目

4日目は Functor則などのモナドの規則をみて、ScalaCheck を用いて任意の型クラスの例を使って検証した。また、Option を Monoid として扱う3つの方法や foldMap などを行う Foldable もみた。

モナドがいっぱい

今日はすごいHaskellたのしく学ぼうの新しい章「モナドがいっぱい」を始めることができる。

モナドはある願いを叶えるための、アプリカティブ値の自然な拡張です。その願いとは、「普通の値 a を取って文脈付きの値を返す関数に、文脈付きの値 m a を渡したい」というものです。

Scalaz でもモナドは Monad と呼ばれている。型クラスのコントラクトはこれだ:

trait Monad[F[_]] extends Applicative[F] with Bind[F] { self =>
  ////
}

これは Applicative と Bind を拡張する。Bind を見てみよう。

Bind

以下が Bind のコントラクトだ:

trait Bind[F[_]] extends Apply[F] { self =>
  /** Equivalent to `join(map(fa)(f))`. */
  def bind[A, B](fa: F[A])(f: A => F[B]): F[B]
}

そして、以下が演算子:

/** Wraps a value `self` and provides methods related to `Bind` */
trait BindOps[F[_],A] extends Ops[F[A]] {
  implicit def F: Bind[F]
  ////
  import Liskov.<~<

  def flatMap[B](f: A => F[B]) = F.bind(self)(f)
  def >>=[B](f: A => F[B]) = F.bind(self)(f)
  def ∗[B](f: A => F[B]) = F.bind(self)(f)
  def join[B](implicit ev: A <~< F[B]): F[B] = F.bind(self)(ev(_))
  def μ[B](implicit ev: A <~< F[B]): F[B] = F.bind(self)(ev(_))
  def >>[B](b: F[B]): F[B] = F.bind(self)(_ => b)
  def ifM[B](ifTrue: => F[B], ifFalse: => F[B])(implicit ev: A <~< Boolean): F[B] = {
    val value: F[Boolean] = Liskov.co[F, A, Boolean](ev)(self)
    F.ifM(value, ifTrue, ifFalse)
  }
  ////
}

flatMap 演算子とシンボルを使ったエイリアス >>= と ∗ を導入する。他の演算子に関しては後回しにしよう。とりあえず標準ライブラリで flatMap は慣れている:

scala> 3.some flatMap { x => (x + 1).some }
res2: Option[Int] = Some(4)

scala> (none: Option[Int]) flatMap { x => (x + 1).some }
res3: Option[Int] = None

Monad

Monad に戻ろう:

trait Monad[F[_]] extends Applicative[F] with Bind[F] { self =>
  ////
}

Haskell と違って Monad[F[_]] は Applicative[F[_]] を継承するため、return と pure と名前が異なるという問題が生じていない。両者とも point だ。

scala> Monad[Option].point("WHAT")
res5: Option[String] = Some(WHAT)

scala> 9.some flatMap { x => Monad[Option].point(x * 10) }
res6: Option[Int] = Some(90)

scala> (none: Option[Int]) flatMap { x => Monad[Option].point(x * 10) }
res7: Option[Int] = None

綱渡り

LYAHFGG:

さて、棒の左右にとまった鳥の数の差が3以内であれば、ピエールはバランスを取れているものとしましょう。例えば、右に1羽、左に4羽の鳥がとまっているなら大丈夫。だけど左に5羽目の鳥がとまったら、ピエールはバランスを崩して飛び降りる羽目になります。

本の Pole の例題を実装してみよう。

scala> type Birds = Int
defined type alias Birds

scala> case class Pole(left: Birds, right: Birds)
defined class Pole

Scala ではこんな風に Int に型エイリアスを付けるのは一般的じゃないと思うけど、ものは試しだ。landLeft と landRight をメソッドをとして実装したいから Pole は case class にする。

scala> case class Pole(left: Birds, right: Birds) {
         def landLeft(n: Birds): Pole = copy(left = left + n)
         def landRight(n: Birds): Pole = copy(right = right + n) 
       }
defined class Pole

OO の方が見栄えが良いと思う:

scala> Pole(0, 0).landLeft(2)
res10: Pole = Pole(2,0)

scala> Pole(1, 2).landRight(1)
res11: Pole = Pole(1,3)

scala> Pole(1, 2).landRight(-1)
res12: Pole = Pole(1,1)

チェインも可能:

scala> Pole(0, 0).landLeft(1).landRight(1).landLeft(2)
res13: Pole = Pole(3,1)

scala> Pole(0, 0).landLeft(1).landRight(4).landLeft(-1).landRight(-2)
res15: Pole = Pole(0,2)

本が言うとおり、中間値で失敗しても計算が続行してしまっている。失敗を Option[Pole] で表現しよう:

scala> case class Pole(left: Birds, right: Birds) {
         def landLeft(n: Birds): Option[Pole] = 
           if (math.abs((left + n) - right) < 4) copy(left = left + n).some
           else none
         def landRight(n: Birds): Option[Pole] =
           if (math.abs(left - (right + n)) < 4) copy(right = right + n).some
           else none
       }
defined class Pole

scala> Pole(0, 0).landLeft(2)
res16: Option[Pole] = Some(Pole(2,0))

scala> Pole(0, 3).landLeft(10)
res17: Option[Pole] = None

flatMap を使ってチェインする:

scala> Pole(0, 0).landRight(1) flatMap {_.landLeft(2)}
res18: Option[Pole] = Some(Pole(2,1))

scala> (none: Option[Pole]) flatMap {_.landLeft(2)}
res19: Option[Pole] = None

scala> Monad[Option].point(Pole(0, 0)) flatMap {_.landRight(2)} flatMap {_.landLeft(2)} flatMap {_.landRight(2)}
res21: Option[Pole] = Some(Pole(2,4))

初期値を Option コンテキストから始めるために Monad[Option].point(...) が使われていることに注意。>>= エイリアスも使うと見た目がモナディックになる:

scala> Monad[Option].point(Pole(0, 0)) >>= {_.landRight(2)} >>= {_.landLeft(2)} >>= {_.landRight(2)}
res22: Option[Pole] = Some(Pole(2,4))

モナディックチェインが綱渡りのシミュレーションを改善したか確かめる:

scala> Monad[Option].point(Pole(0, 0)) >>= {_.landLeft(1)} >>= {_.landRight(4)} >>= {_.landLeft(-1)} >>= {_.landRight(-2)}
res23: Option[Pole] = None

うまくいった。

ロープの上のバナナ

LYAHFGG:

さて、今度はバランス棒にとまっている鳥の数によらず、いきなりピエールを滑らせて落っことす関数を作ってみましょう。この関数を banana と呼ぶことにします。

以下が常に失敗する banana だ:

scala> case class Pole(left: Birds, right: Birds) {
         def landLeft(n: Birds): Option[Pole] = 
           if (math.abs((left + n) - right) < 4) copy(left = left + n).some
           else none
         def landRight(n: Birds): Option[Pole] =
           if (math.abs(left - (right + n)) < 4) copy(right = right + n).some
           else none
         def banana: Option[Pole] = none
       }
defined class Pole

scala> Monad[Option].point(Pole(0, 0)) >>= {_.landLeft(1)} >>= {_.banana} >>= {_.landRight(1)}
res24: Option[Pole] = None

LYAHFGG:

ところで、入力に関係なく既定のモナド値を返す関数だったら、自作せずとも >> 関数を使うという手があります。

以下が >> の Option での振る舞い:

scala> (none: Option[Int]) >> 3.some
res25: Option[Int] = None

scala> 3.some >> 4.some
res26: Option[Int] = Some(4)

scala> 3.some >> (none: Option[Int])
res27: Option[Int] = None

banana を >> (none: Option[Pole]) に置き換えてみよう:

scala> Monad[Option].point(Pole(0, 0)) >>= {_.landLeft(1)} >> (none: Option[Pole]) >>= {_.landRight(1)}
<console>:26: error: missing parameter type for expanded function ((x$1) => x$1.landLeft(1))
              Monad[Option].point(Pole(0, 0)) >>= {_.landLeft(1)} >> (none: Option[Pole]) >>= {_.landRight(1)}
                                                   ^

突然型推論が崩れてしまった。問題の原因はおそらく演算子の優先順位にある。 Programming in Scala 曰く:

The one exception to the precedence rule, alluded to above, concerns assignment operators, which end in an equals character. If an operator ends in an equals character (=), and the operator is not one of the comparison operators <=, >=, ==, or !=, then the precedence of the operator is the same as that of simple assignment (=). That is, it is lower than the precedence of any other operator.

注意: 上記の記述は不完全だ。代入演算子ルールのもう1つの例外は演算子が === のように (=) から始まる場合だ。

>>= (bind) が等号で終わるため、優先順位は最下位に落とされ、({_.landLeft(1)} >> (none: Option[Pole])) が先に評価される。いくつかの気が進まない回避方法がある。まず、普通のメソッド呼び出しのようにドットと括弧の記法を使うことができる:

scala> Monad[Option].point(Pole(0, 0)).>>=({_.landLeft(1)}).>>(none: Option[Pole]).>>=({_.landRight(1)})
res9: Option[Pole] = None

もしくは優先順位の問題に気付いたなら、適切な場所に括弧を置くことができる:

scala> (Monad[Option].point(Pole(0, 0)) >>= {_.landLeft(1)}) >> (none: Option[Pole]) >>= {_.landRight(1)}
res10: Option[Pole] = None

両方とも正しい答が得られた。ちなみに、>>= を flatMap に変えても >> の方がまだ優先順位が高いため問題は解決しない。

for 構文

LYAHFGG:

Haskell にとってモナドはとても便利なので、モナド専用構文まで用意されています。その名は do 記法。

まずは入れ子のラムダ式を書いてみよう:

scala> 3.some >>= { x => "!".some >>= { y => (x.shows + y).some } }
res14: Option[String] = Some(3!)

>>= が使われたことで計算のどの部分も失敗することができる:

scala> 3.some >>= { x => (none: Option[String]) >>= { y => (x.shows + y).some } }
res17: Option[String] = None

scala> (none: Option[Int]) >>= { x => "!".some >>= { y => (x.shows + y).some } }
res16: Option[String] = None

scala> 3.some >>= { x => "!".some >>= { y => (none: Option[String]) } }
res18: Option[String] = None

Haskell の do 記法のかわりに、Scala には for 構文があり、これらは同じものだ:

scala> for {
         x <- 3.some
         y <- "!".some
       } yield (x.shows + y)
res19: Option[String] = Some(3!)

LYAHFGG:

do 式は、let 行を除いてすべてモナド値で構成されます。

これも Scala の for 構文に当てはまると思う。

帰ってきたピエール

LYAHFGG:

ピエールの綱渡りの動作も、もちろん do 記法で書けます。

scala> def routine: Option[Pole] =
         for {
           start <- Monad[Option].point(Pole(0, 0))
           first <- start.landLeft(2)
           second <- first.landRight(2)
           third <- second.landLeft(1)
         } yield third
routine: Option[Pole]

scala> routine
res20: Option[Pole] = Some(Pole(3,2))

yield は Option[Pole] じゃなくて Pole を受け取るため、third も抽出する必要があった。

LYAHFGG:

ピエールにバナナの皮を踏ませたい場合、do 記法ではこう書きます。

scala> def routine: Option[Pole] =
         for {
           start <- Monad[Option].point(Pole(0, 0))
           first <- start.landLeft(2)
           _ <- (none: Option[Pole])
           second <- first.landRight(2)
           third <- second.landLeft(1)
         } yield third
routine: Option[Pole]

scala> routine
res23: Option[Pole] = None

パターンマッチングと失敗

LYAHFGG:

do 記法でモナド値を変数名に束縛するときには、let 式や関数の引数のときと同様、パターンマッチが使えます。

scala> def justH: Option[Char] =
         for {
           (x :: xs) <- "hello".toList.some
         } yield x
justH: Option[Char]

scala> justH
res25: Option[Char] = Some(h)

do 式の中でパターンマッチが失敗した場合、Monad 型クラスの一員である fail 関数が使われるので、異常終了という形ではなく、そのモナドの文脈に合った形で失敗を処理できます。

scala> def wopwop: Option[Char] =
         for {
           (x :: xs) <- "".toList.some
         } yield x
wopwop: Option[Char]

scala> wopwop
res28: Option[Char] = None

失敗したパターンマッチングは None を返している。これは for 構文の興味深い一面で、今まで考えたことがなかったが、言われるとなるほどと思う。

List モナド

LYAHFGG:

一方、[3,8,9] のような値は複数の計算結果を含んでいるとも、複数の候補値を同時に重ね合わせたような1つの値であるとも解釈できます。リストをアプリカティブ・スタイルで使うと、非決定性を表現していることがはっきりします。

まずは Applicative としての List を復習する:

scala> ^(List(1, 2, 3), List(10, 100, 100)) {_ * _}
res29: List[Int] = List(10, 100, 100, 20, 200, 200, 30, 300, 300)

それでは、非決定的値を関数に食わせてみましょう。

scala> List(3, 4, 5) >>= {x => List(x, -x)}
res30: List[Int] = List(3, -3, 4, -4, 5, -5)

モナディックな視点に立つと、List というコンテキストは複数の解がありうる数学的な値を表す。それ以外は、for を使って List を操作するなどは素の Scala と変わらない:

scala> for {
         n <- List(1, 2)
         ch <- List('a', 'b')
       } yield (n, ch)
res33: List[(Int, Char)] = List((1,a), (1,b), (2,a), (2,b))

MonadPlus と guard 関数

Scala の for 構文はフィルタリングができる:

scala> for {
         x <- 1 |-> 50 if x.shows contains '7'
       } yield x
res40: List[Int] = List(7, 17, 27, 37, 47)

LYAHFGG:

MonadPlus は、モノイドの性質をあわせ持つモナドを表す型クラスです。

以下が MonadPlus の型クラスのコントラクトだ:

trait MonadPlus[F[_]] extends Monad[F] with ApplicativePlus[F] { self =>
  ...
}

Plus、PlusEmpty、と ApplicativePlus

これは ApplicativePlus を継承している:

trait ApplicativePlus[F[_]] extends Applicative[F] with PlusEmpty[F] { self =>
  ...
}

そして、それは PlusEmpty を継承している:

trait PlusEmpty[F[_]] extends Plus[F] { self =>
  ////
  def empty[A]: F[A]
}

そして、それは Plus を継承している:

trait Plus[F[_]]  { self =>
  def plus[A](a: F[A], b: => F[A]): F[A]
}

Semigroup[A] と Monoid[A] 同様に、Plus[F[_]] と PlusEmpty[F[_]] はそれらのインスタンスが plus と empty を実装することを要請する。違いはこれが型コンストラクタ (F[_]) レベルであることだ。

Plus は 2つのコンテナを連結する <+> 演算子を導入する:

scala> List(1, 2, 3) <+> List(4, 5, 6)
res43: List[Int] = List(1, 2, 3, 4, 5, 6)

MonadPlus 再び

MonadPlus は filter 演算を導入する。

scala> (1 |-> 50) filter { x => x.shows contains '7' }
res46: List[Int] = List(7, 17, 27, 37, 47)

騎士の旅

LYAHFGG:

ここで、非決定性計算を使って解くのにうってつけの問題をご紹介しましょう。チェス盤の上にナイトの駒が1つだけ乗っています。ナイトを3回動かして特定のマスまで移動させられるか、というのが問題です。

ペアに型エイリアスと付けるかわりにまた case class にしよう:

scala> case class KnightPos(c: Int, r: Int)
defined class KnightPos

以下がナイトの次に取りうる位置を全て計算する関数だ:

scala> case class KnightPos(c: Int, r: Int) {
         def move: List[KnightPos] =
           for {
             KnightPos(c2, r2) <- List(KnightPos(c + 2, r - 1), KnightPos(c + 2, r + 1),
               KnightPos(c - 2, r - 1), KnightPos(c - 2, r + 1),
               KnightPos(c + 1, r - 2), KnightPos(c + 1, r + 2),
               KnightPos(c - 1, r - 2), KnightPos(c - 1, r + 2)) if (
               ((1 |-> 8) contains c2) && ((1 |-> 8) contains r2))
           } yield KnightPos(c2, r2)
       }
defined class KnightPos

scala> KnightPos(6, 2).move
res50: List[KnightPos] = List(KnightPos(8,1), KnightPos(8,3), KnightPos(4,1), KnightPos(4,3), KnightPos(7,4), KnightPos(5,4))

scala> KnightPos(8, 1).move
res51: List[KnightPos] = List(KnightPos(6,2), KnightPos(7,3))

答は合ってるみたいだ。次に、3回のチェインを実装する:

scala> case class KnightPos(c: Int, r: Int) {
         def move: List[KnightPos] =
           for {
             KnightPos(c2, r2) <- List(KnightPos(c + 2, r - 1), KnightPos(c + 2, r + 1),
             KnightPos(c - 2, r - 1), KnightPos(c - 2, r + 1),
             KnightPos(c + 1, r - 2), KnightPos(c + 1, r + 2),
             KnightPos(c - 1, r - 2), KnightPos(c - 1, r + 2)) if (
             ((1 |-> 8) element c2) && ((1 |-> 8) contains r2))
           } yield KnightPos(c2, r2)
         def in3: List[KnightPos] =
           for {
             first <- move
             second <- first.move
             third <- second.move
           } yield third
         def canReachIn3(end: KnightPos): Boolean = in3 contains end
       }
defined class KnightPos

scala> KnightPos(6, 2) canReachIn3 KnightPos(6, 1)
res56: Boolean = true

scala> KnightPos(6, 2) canReachIn3 KnightPos(7, 3)
res57: Boolean = false

Monad則

左単位元

LYAHFGG:

第一のモナド則が言っているのは、return を使って値をデフォルトの文脈に入れたものを >>= を使って関数に食わせた結果は、単にその値にその関数を適用した結果と等しくなりなさい、ということです。

これを Scala で表現すると、

// (Monad[F].point(x) flatMap {f}) assert_=== f(x)

scala> (Monad[Option].point(3) >>= { x => (x + 100000).some }) assert_=== 3 |> { x => (x + 100000).some }

右単位元

モナドの第二法則は、>>= を使ってモナド値を return に食わせた結果は、元のモナド値と不変であると言っています。

// (m forMap {Monad[F].point(_)}) assert_=== m

scala> ("move on up".some flatMap {Monad[Option].point(_)}) assert_=== "move on up".some

結合律

最後のモナド則は、>>= を使ったモナド関数適用の連鎖があるときに、どの順序で評価しても結果は同じであるべき、というものです。

// (m flatMap f) flatMap g assert_=== m flatMap { x => f(x) flatMap {g} }

scala> Monad[Option].point(Pole(0, 0)) >>= {_.landRight(2)} >>= {_.landLeft(2)} >>= {_.landRight(2)}
res76: Option[Pole] = Some(Pole(2,4))

scala> Monad[Option].point(Pole(0, 0)) >>= { x =>
       x.landRight(2) >>= { y =>
       y.landLeft(2) >>= { z =>
       z.landRight(2)
       }}}
res77: Option[Pole] = Some(Pole(2,4))

Scalaz 7 はモナド則を以下のように表現する:

  trait MonadLaw extends ApplicativeLaw {
    /** Lifted `point` is a no-op. */
    def rightIdentity[A](a: F[A])(implicit FA: Equal[F[A]]): Boolean = FA.equal(bind(a)(point(_: A)), a)
    /** Lifted `f` applied to pure `a` is just `f(a)`. */
    def leftIdentity[A, B](a: A, f: A => F[B])(implicit FB: Equal[F[B]]): Boolean = FB.equal(bind(point(a))(f), f(a))
    /**
     * As with semigroups, monadic effects only change when their
     * order is changed, not when the order in which they're
     * combined changes.
     */
    def associativeBind[A, B, C](fa: F[A], f: A => F[B], g: B => F[C])(implicit FC: Equal[F[C]]): Boolean =
      FC.equal(bind(bind(fa)(f))(g), bind(fa)((a: A) => bind(f(a))(g)))
  }

以下が Option がモナド則に従うかを検証する方法だ。 4日目の build.sbt を用いて sbt test:console を実行する:

scala> monad.laws[Option].check
+ monad.applicative.functor.identity: OK, passed 100 tests.
+ monad.applicative.functor.associative: OK, passed 100 tests.
+ monad.applicative.identity: OK, passed 100 tests.
+ monad.applicative.composition: OK, passed 100 tests.
+ monad.applicative.homomorphism: OK, passed 100 tests.
+ monad.applicative.interchange: OK, passed 100 tests.
+ monad.right identity: OK, passed 100 tests.
+ monad.left identity: OK, passed 100 tests.
+ monad.associativity: OK, passed 100 tests.

Option よくできました。続きはここから。

6日目

昨日は、flatMap を導入する Monad 型クラスをみた。また、モナディックなチェインが値にコンテキストを与えることも確認した。Option も List も標準ライブラリに flatMap があるから、新しいコードというよりは今まであったものに対して視点を変えて見るという感じになった。あと、モナディックな演算をチェインする方法としての for 構文も確認した。

for 構文、再び

Haskell の do 記法と Scala の for 構文には微妙な違いがある。以下が do 表記の例:

foo = do
  x <- Just 3
  y <- Just "!"
  Just (show x ++ y)

通常は return (show x ++ y) と書くと思うけど、最後の行がモナディックな値であることを強調するために Just を書き出した。一方 Scala はこうだ:

scala> def foo = for {
         x <- 3.some
         y <- "!".some
       } yield x.shows + y

ほぼ同じに見えるけど、Scala の x.shows + y は素の String で、yield が強制的にその値をコンテキストに入れている。これは生の値があればうまくいく。だけど、モナディックな値を返す関数があった場合はどうすればいいだろう?

in3 start = do
  first <- moveKnight start
  second <- moveKnight first
  moveKnight second

これは Scala では moveKnight second の値を抽出して yield で再包装せずには書くことができない。

def in3: List[KnightPos] = for {
  first <- move
  second <- first.move
  third <- second.move
} yield third

この違いにより問題が生じることは実際には無いかもしれないけど、一応覚えておいたほうがいいと思う。

Writer? 中の人なんていません!

すごいHaskellたのしく学ぼう曰く:

Maybe モナドが失敗の可能性という文脈付きの値を表し、リストモナドが非決定性が付いた値を表しているのに対し、Writer モナドは、もう1つの値がくっついた値を表し、付加された値はログのように振る舞います。

本に従って applyLog 関数を実装してみよう:

scala> def isBigGang(x: Int): (Boolean, String) =
         (x > 9, "Compared gang size to 9.")
isBigGang: (x: Int)(Boolean, String)

scala> implicit class PairOps[A](pair: (A, String)) {
         def applyLog[B](f: A => (B, String)): (B, String) = {
           val (x, log) = pair
           val (y, newlog) = f(x)
           (y, log ++ newlog)
         }
       }
defined class PairOps

scala> (3, "Smallish gang.") applyLog isBigGang
res30: (Boolean, String) = (false,Smallish gang.Compared gang size to 9.)

メソッドの注入が implicit のユースケースとしては多いため、Scala 2.10 に implicit class という糖衣構文が登場して、クラスから強化クラスに昇進させるのが簡単になった。ログを Monoid として一般化する:

scala> implicit class PairOps[A, B: Monoid](pair: (A, B)) {
         def applyLog[C](f: A => (C, B)): (C, B) = {
           val (x, log) = pair
           val (y, newlog) = f(x)
           (y, log |+| newlog)
         }
       }
defined class PairOps

scala> (3, "Smallish gang.") applyLog isBigGang
res31: (Boolean, String) = (false,Smallish gang.Compared gang size to 9.)

Writer

LYAHFGG:

値にモノイドのおまけを付けるには、タプルに入れるだけです。Writer w a 型の実体は、そんなタプルの newtype ラッパーにすぎず、定義はとてもシンプルです。

Scalaz でこれに対応するのは Writer だ:

type Writer[+W, +A] = WriterT[Id, W, A]

Writer[+W, +A] は、WriterT[Id, W, A] の型エイリアスだ。

WriterT

以下が WriterT を単純化したものだ:

sealed trait WriterT[F[+_], +W, +A] { self =>
  val run: F[(W, A)]

  def written(implicit F: Functor[F]): F[W] =
    F.map(run)(_._1)
  def value(implicit F: Functor[F]): F[A] =
    F.map(run)(_._2)
}

Writer が実際にどうやって作られるのかは直ぐには分からなかったけど、見つけることができた:

scala> 3.set("Smallish gang.")
res46: scalaz.Writer[String,Int] = scalaz.WriterTFunctions$$anon$26@477a0c05

import Scalaz._ によって全てのデータ型に対して以下の演算子が導入される:

trait ToDataOps extends ToIdOps with ToTreeOps with ToWriterOps with ToValidationOps with ToReducerOps with ToKleisliOps

件の演算子は WriterOps の一部だ:

final class WriterOps[A](self: A) {
  def set[W](w: W): Writer[W, A] = WriterT.writer(w -> self)

  def tell: Writer[A, Unit] = WriterT.tell(self)
}

上のメソッドは全ての型に注入されるため、以下のように Writer を作ることができる:

scala> 3.set("something")
res57: scalaz.Writer[String,Int] = scalaz.WriterTFunctions$$anon$26@159663c3

scala> "something".tell
res58: scalaz.Writer[String,Unit] = scalaz.WriterTFunctions$$anon$26@374de9cf

return 3 :: Writer String Int のように単位元が欲しい場合はどうすればいいだろう? Monad[F[_]] は型パラメータが 1つの型コンストラクタを期待するけど、Writer[+W, +A] は 2つある。Scalaz にある MonadTell というヘルパー型を使うと簡単にモナドが得られる (以前は MonadWriter という名前だった):

scala> MonadTell[Writer, String]
res62: scalaz.MonadTell[scalaz.Writer,String] = scalaz.WriterTInstances$$anon$1@6b8501fa

scala> MonadTell[Writer, String].point(3).run
res64: (String, Int) = ("",3)

Writer に for 構文を使う

LYAHFGG:

こうして Monad インスタンスができたので、Writer を do 記法で自由に扱えます。

例題を Scala で実装してみよう:

scala> def logNumber(x: Int): Writer[List[String], Int] =
         x.set(List("Got number: " + x.shows))
logNumber: (x: Int)scalaz.Writer[List[String],Int]

scala> def multWithLog: Writer[List[String], Int] = for {
         a <- logNumber(3)
         b <- logNumber(5)
       } yield a * b
multWithLog: scalaz.Writer[List[String],Int]

scala> multWithLog.run
res67: (List[String], Int) = (List(Got number: 3, Got number: 5),15)

プログラムにログを追加する

以下が例題の gcd だ:

scala> :paste
// Entering paste mode (ctrl-D to finish)

def gcd(a: Int, b: Int): Writer[List[String], Int] =
  if (b == 0) for {
      _ <- List("Finished with " + a.shows).tell
    } yield a
  else
    List(a.shows + " mod " + b.shows + " = " + (a % b).shows).tell >>= { _ =>
      gcd(b, a % b)
    }

// Exiting paste mode, now interpreting.

gcd: (a: Int, b: Int)scalaz.Writer[List[String],Int]

scala> gcd(8, 3).run
res71: (List[String], Int) = (List(8 mod 3 = 2, 3 mod 2 = 1, 2 mod 1 = 0, Finished with 1),1)

非効率な List の構築

LYAHFGG:

Writer モナドを使うときは、使うモナドに気をつけてください。リストを使うととても遅くなる場合があるからです。リストは mappend に ++ を使っていますが、++ を使ってリストの最後にものを追加する操作は、そのリストがとても長いと遅くなってしまいます。

主なコレクションの性能特性をまとめた表があるので見てみよう。不変コレクションで目立っているのが全ての演算を実質定数でこなす Vector だ。Vector は分岐度が 32 の木構造で、構造共有を行うことで高速な更新を実現している。

scala> Monoid[Vector[String]]
res73: scalaz.Monoid[Vector[String]] = scalaz.std.IndexedSeqSubInstances$$anon$4@6f82f06f

Vector を使った gcd:

scala> :paste
// Entering paste mode (ctrl-D to finish)

def gcd(a: Int, b: Int): Writer[Vector[String], Int] =
  if (b == 0) for {
      _ <- Vector("Finished with " + a.shows).tell
    } yield a
  else for {
      result <- gcd(b, a % b)
      _ <- Vector(a.shows + " mod " + b.shows + " = " + (a % b).shows).tell
    } yield result

// Exiting paste mode, now interpreting.

gcd: (a: Int, b: Int)scalaz.Writer[Vector[String],Int]

scala> gcd(8, 3).run
res74: (Vector[String], Int) = (Vector(Finished with 1, 2 mod 1 = 0, 3 mod 2 = 1, 8 mod 3 = 2),1)

性能の比較

本のように性能を比較するマイクロベンチマークを書いてみよう:

def vectorFinalCountDown(x: Int): Writer[Vector[String], Unit] = {
  import annotation.tailrec
  @tailrec def doFinalCountDown(x: Int, w: Writer[Vector[String], Unit]): Writer[Vector[String], Unit] = x match {
    case 0 => w >>= { _ => Vector("0").tell }
    case x => doFinalCountDown(x - 1, w >>= { _ =>
      Vector(x.shows).tell
    })
  }
  val t0 = System.currentTimeMillis
  val r = doFinalCountDown(x, Vector[String]().tell)
  val t1 = System.currentTimeMillis
  r >>= { _ => Vector((t1 - t0).shows + " msec").tell }
}

def listFinalCountDown(x: Int): Writer[List[String], Unit] = {
  import annotation.tailrec
  @tailrec def doFinalCountDown(x: Int, w: Writer[List[String], Unit]): Writer[List[String], Unit] = x match {
    case 0 => w >>= { _ => List("0").tell }
    case x => doFinalCountDown(x - 1, w >>= { _ =>
      List(x.shows).tell
    })
  }
  val t0 = System.currentTimeMillis
  val r = doFinalCountDown(x, List[String]().tell)
  val t1 = System.currentTimeMillis
  r >>= { _ => List((t1 - t0).shows + " msec").tell }
}

以下のように実行できる:

scala> vectorFinalCountDown(10000).run
res18: (Vector[String], Unit) = (Vector(10000, 9999, 9998, 9997, 9996, 9995, 9994, 9993, 9992, 9991, 9990, 9989, 9988, 9987, 9986, 9985, 9984, ...

scala> res18._1.last
res19: String = 1206 msec

scala> listFinalCountDown(10000).run
res20: (List[String], Unit) = (List(10000, 9999, 9998, 9997, 9996, 9995, 9994, 9993, 9992, 9991, 9990, 9989, 9988, 9987, 9986, 9985, 9984, ...
scala> res20._1.last

res21: String = 2050 msec

List に倍近くの時間がかかっているのが分かる。

Reader

LYAHFGG:

第11章では、関数を作る型、(->) r も、Functor のインスタンスであることを見ました。

scala> val f = (_: Int) * 5
f: Int => Int = <function1>

scala> val g = (_: Int) + 3
g: Int => Int = <function1>

scala> (g map f)(8)
res22: Int = 55

それから、関数はアプリカティブファンクターであることも見ましたね。これにより、関数が将来返すであろう値を、すでに持っているかのように演算できるようになりました。

scala> val f = ({(_: Int) * 2} |@| {(_: Int) + 10}) {_ + _}
warning: there were 1 deprecation warnings; re-run with -deprecation for details
f: Int => Int = <function1>

scala> f(3)
res35: Int = 19

関数の型 (->) r はファンクターであり、アプリカティブファンクターであるばかりでなく、モナドでもあります。これまでに登場したモナド値と同様、関数もまた文脈を持った値だとみなすことができるのです。関数にとっての文脈とは、値がまだ手元になく、値が欲しければその関数を別の何かに適用しないといけない、というものです。

この例題も実装してみよう:

scala> val addStuff: Int => Int = for {
         a <- (_: Int) * 2
         b <- (_: Int) + 10
       } yield a + b
addStuff: Int => Int = <function1>

scala> addStuff(3)
res39: Int = 19

(*2) と (+10) はどちらも 3 に適用されます。実は、return (a+b) も同じく 3 に適用されるんですが、引数を無視して常に a+b を返しています。そいういうわけで、関数モナドは Reader モナドとも呼ばれたりします。すべての関数が共通の情報を「読む」からです。

要は、Reader モナドは値が既にあるかのようなフリをさせてくれる。恐らくこれは1つのパラメータを受け取る関数でしか使えないと予想している。Option や List モナドと違って、Writer も Reader モナドも標準ライブラリには入っていないし、便利そうだ。

続きはまたここから。

7日目

6日目は、for 構文をみて、Writer モナドと関数をモナドとして扱うリーダーモナドをみた。

Applicative Builder

実はリーダーモナドの話をしながらこっそり Applicative builder |@| を使った。2日目に 7.0.0-M3 から新しく導入された ^(f1, f2) {...} スタイルを紹介したけど、関数などの 2つの型パラメータを取る型コンストラクタでうまく動作しないみたいことが分かった。

Scalaz のメーリングリストを見ると |@| は deprecate 状態から復活するらしいので、これからはこのスタイルを使おう:

scala> (3.some |@| 5.some) {_ + _}
res18: Option[Int] = Some(8)

scala> val f = ({(_: Int) * 2} |@| {(_: Int) + 10}) {_ + _}
f: Int => Int = <function1>

計算の状態の正体

すごいHaskellたのしく学ぼう曰く:

そこで Haskell には State モナドが用意されています。これさえあれば、状態付きの計算などいとも簡単。しかもすべてを純粋に保ったまま扱えるんです。

スタックの例題を実装してみよう。今回は case class を作らずに Haskell を Scala に直訳してみる:

scala> type Stack = List[Int]
defined type alias Stack

scala> def pop(stack: Stack): (Int, Stack) = stack match {
         case x :: xs => (x, xs)
       }
pop: (stack: Stack)(Int, Stack)

scala> def push(a: Int, stack: Stack): (Unit, Stack) = ((), a :: stack)
push: (a: Int, stack: Stack)(Unit, Stack)

scala> def stackManip(stack: Stack): (Int, Stack) = {
         val (_, newStack1) = push(3, stack)
         val (a, newStack2) = pop(newStack1)
         pop(newStack2)
       }
stackManip: (stack: Stack)(Int, Stack)

scala> stackManip(List(5, 8, 2, 1))
res0: (Int, Stack) = (5,List(8, 2, 1))

State and StateT

LYAHFGG:

状態付きの計算とは、ある状態を取って、更新された状態と一緒に計算結果を返す関数として表現できるでしょう。そんな関数の型は、こうなるはずです。

s -> (a, s)

ここで大切なのは、今まで見てきた汎用のモナドと違って State は関数をラッピングすることに特化していることだ。Scalaz での State の定義をみてみよう:

  type State[S, +A] = StateT[Id, S, A]

  // important to define here, rather than at the top-level, to avoid Scala 2.9.2 bug
  object State extends StateFunctions {
    def apply[S, A](f: S => (S, A)): State[S, A] = new StateT[Id, S, A] {
      def apply(s: S) = f(s)
    }
  }

Writer 同様に、State[S, +A] は StateT[Id, S, A] の型エイリアスだ。以下が StateT の簡易版だ:

trait StateT[F[+_], S, +A] { self =>
  /** Run and return the final value and state in the context of `F` */
  def apply(initial: S): F[(S, A)]

  /** An alias for `apply` */
  def run(initial: S): F[(S, A)] = apply(initial)

  /** Calls `run` using `Monoid[S].zero` as the initial state */
  def runZero(implicit S: Monoid[S]): F[(S, A)] =
    run(S.zero)
}

新しい状態は State シングルトンを使って構築する:

scala> State[List[Int], Int] { case x :: xs => (xs, x) }
res1: scalaz.State[List[Int],Int] = scalaz.package$State$$anon$1@19f58949

スタックを State を使って実装してみよう:

scala> type Stack = List[Int]
defined type alias Stack

scala> val pop = State[Stack, Int] {
         case x :: xs => (xs, x)
       }
pop: scalaz.State[Stack,Int]

scala> def push(a: Int) = State[Stack, Unit] {
         case xs => (a :: xs, ())
       }
push: (a: Int)scalaz.State[Stack,Unit]

scala> def stackManip: State[Stack, Int] = for {
         _ <- push(3)
         a <- pop
         b <- pop
       } yield(b)
stackManip: scalaz.State[Stack,Int]

scala> stackManip(List(5, 8, 2, 1))
res2: (Stack, Int) = (List(8, 2, 1),5)

State[List[Int], Int] {...} を用いて「状態を抽出して、値と状態を返す」というコードの部分を抽象化することができた。強力なのは for 構文を使ってぞれぞれの演算を State を引き回さずにモナディックに連鎖できることだ。上の stackManip がそのいい例だ。

状態の取得と設定

LYAHFGG:

Control.Monad.State モジュールは、2つの便利な関数 get と put を備えた、MonadState という型クラスを提供しています。

State object は StateFunctions trait を継承して、いくつかのヘルパー関数を定義する:

trait StateFunctions {
  def constantState[S, A](a: A, s: => S): State[S, A] =
    State((_: S) => (s, a))
  def state[S, A](a: A): State[S, A] =
    State((_ : S, a))
  def init[S]: State[S, S] = State(s => (s, s))
  def get[S]: State[S, S] = init
  def gets[S, T](f: S => T): State[S, T] = State(s => (s, f(s)))
  def put[S](s: S): State[S, Unit] = State(_ => (s, ()))
  def modify[S](f: S => S): State[S, Unit] = State(s => {
    val r = f(s);
    (r, ())
  })
  /**
   * Computes the difference between the current and previous values of `a`
   */
  def delta[A](a: A)(implicit A: Group[A]): State[A, A] = State{
    (prevA) =>
      val diff = A.minus(a, prevA)
      (diff, a)
  }
}

ちょっと最初は分かりづらかった。だけど、State モナドは「状態を受け取り値と状態を返す」関数をカプセル化していることを思い出してほしい。そのため、状態というコンテキストでの get は状態から値を取得するというだけの話だ:

  def init[S]: State[S, S] = State(s => (s, s))
  def get[S]: State[S, S] = init

そして、このコンテキストでの put は何からの値を状態に設定するということを指す:

  def put[S](s: S): State[S, Unit] = State(_ => (s, ()))

stackStack 関数を実装して具体例でみてみよう。

scala> def stackyStack: State[Stack, Unit] = for {
         stackNow <- get
         r <- if (stackNow === List(1, 2, 3)) put(List(8, 3, 1))
              else put(List(9, 2, 1))
       } yield r
stackyStack: scalaz.State[Stack,Unit]

scala> stackyStack(List(1, 2, 3))
res4: (Stack, Unit) = (List(8, 3, 1),())

pop と push も get と put を使って実装できる:

scala> val pop: State[Stack, Int] = for {
         s <- get[Stack]
         val (x :: xs) = s
         _ <- put(xs)
       } yield x
pop: scalaz.State[Stack,Int] = scalaz.StateT$$anon$7@40014da3

scala> def push(x: Int): State[Stack, Unit] = for {
         xs <- get[Stack]
         r <- put(x :: xs)
       } yield r
push: (x: Int)scalaz.State[Stack,Unit]

見ての通りモナドそのものはあんまり大したこと無い (タプルを返す関数のカプセル化) けど、連鎖することでボイラープレートを省くことができた。

\/

LYAHFGG:

Either e a 型も失敗の文脈を与えるモナドです。しかも、失敗に値を付加できるので、何が失敗したかを説明したり、そのほか失敗にまつわる有用な情報を提供できます。

標準ライブラリの Either[A, B] は知ってるけど、Scalaz 7 は Either に対応する独自のデータ構造 \/ を提供する:

sealed trait \/[+A, +B] {
  ...
  /** Return `true` if this disjunction is left. */
  def isLeft: Boolean =
    this match {
      case -\/(_) => true
      case \/-(_) => false
    }

  /** Return `true` if this disjunction is right. */
  def isRight: Boolean =
    this match {
      case -\/(_) => false
      case \/-(_) => true
    }
  ...
  /** Flip the left/right values in this disjunction. Alias for `unary_~` */
  def swap: (B \/ A) =
    this match {
      case -\/(a) => \/-(a)
      case \/-(b) => -\/(b)
    }
  /** Flip the left/right values in this disjunction. Alias for `swap` */
  def unary_~ : (B \/ A) = swap
  ...
  /** Return the right value of this disjunction or the given default if left. Alias for `|` */
  def getOrElse[BB >: B](x: => BB): BB =
    toOption getOrElse x
  /** Return the right value of this disjunction or the given default if left. Alias for `getOrElse` */
  def |[BB >: B](x: => BB): BB = getOrElse(x)
  
  /** Return this if it is a right, otherwise, return the given value. Alias for `|||` */
  def orElse[AA >: A, BB >: B](x: => AA \/ BB): AA \/ BB =
    this match {
      case -\/(_) => x
      case \/-(_) => this
    }
  /** Return this if it is a right, otherwise, return the given value. Alias for `orElse` */
  def |||[AA >: A, BB >: B](x: => AA \/ BB): AA \/ BB = orElse(x)
  ...
}

private case class -\/[+A](a: A) extends (A \/ Nothing)
private case class \/-[+B](b: B) extends (Nothing \/ B)

これらの値は IdOps 経由で全てのデータ型に注入された right メソッドと left メソッドによって作られる:

scala> 1.right[String]
res12: scalaz.\/[String,Int] = \/-(1)

scala> "error".left[Int]
res13: scalaz.\/[String,Int] = -\/(error)

Scala 標準ライブラリの Either 型はそれ単体ではモナドではないため、Scalaz を使っても使わなくても flatMap メソッドを実装しない:

scala> Left[String, Int]("boom") flatMap { x => Right[String, Int](x + 1) }
<console>:8: error: value flatMap is not a member of scala.util.Left[String,Int]
              Left[String, Int]("boom") flatMap { x => Right[String, Int](x + 1) }
                                        ^

right メソッドを呼んで RightProjection に変える必要がある:

scala> Left[String, Int]("boom").right flatMap { x => Right[String, Int](x + 1)}
res15: scala.util.Either[String,Int] = Left(boom)

Either がそもそも存在する理由は左のエラーを報告するためにあるのだから、いちいち right を呼ぶのは手間だ。Scalaz の \/ はだいたいにおいて右投射が欲しいだろうと決めてかかってくれる:

scala> "boom".left[Int] >>= { x => (x + 1).right }
res18: scalaz.Unapply[scalaz.Bind,scalaz.\/[String,Int]]{type M[X] = scalaz.\/[String,X]; type A = Int}#M[Int] = -\/(boom)

これは便利だ。for 構文から使ってみよう:

scala> for {
         e1 <- "event 1 ok".right
         e2 <- "event 2 failed!".left[String]
         e3 <- "event 3 failed!".left[String]
       } yield (e1 |+| e2 |+| e3)
res24: scalaz.\/[String,String] = -\/(event 2 failed!)

見ての通り、最初の失敗が最終結果に繰り上がった。\/ からどうやって値を取り出せばいい? まず、isRight と isLeft でどっち側にいるか確かめる:

scala> "event 1 ok".right.isRight
res25: Boolean = true

scala> "event 1 ok".right.isLeft
res26: Boolean = false

右値なら getOrElse もしくはそのシンボルを使ったエイリアス | を使う:

scala> "event 1 ok".right | "something bad"
res27: String = event 1 ok

左値なら swap メソッドもしくはそのシンボルを使ったエイリアス unary_~ を使う:

scala> ~"event 2 failed!".left[String] | "something good"
res28: String = event 2 failed!

map を使って右の値を変更できる:

scala> "event 1 ok".right map {_ + "!"}
res31: scalaz.\/[Nothing,String] = \/-(event 1 ok!)

左側で連鎖させるには、=> AA \/ BB (ただし [AA >: A, BB >: B]) を受け取る orElse がある。orElse のシンボルを使ったエイリアスは ||| だ:

scala> "event 1 failed!".left ||| "retry event 1 ok".right 
res32: scalaz.\/[String,String] = \/-(retry event 1 ok)

Validation

Scalaz のデータ構造で Either と比較されるものにもう1つ Validation がある:

sealed trait Validation[+E, +A] {
  /** Return `true` if this validation is success. */
  def isSuccess: Boolean = this match {
    case Success(_) => true
    case Failure(_) => false
  }
  /** Return `true` if this validation is failure. */
  def isFailure: Boolean = !isSuccess

  ...
}

final case class Success[E, A](a: A) extends Validation[E, A]
final case class Failure[E, A](e: E) extends Validation[E, A]

一見すると Validation は \/ に似ている。お互い validation メソッドと disjunction メソッドを使って変換することまでできる。

ValidationOps によって全てのデータ型に success[X]、 successNel[X]、failure[X]、failureNel[X] メソッドが導入されている (今のところ Nel に関しては心配しなくていい):

scala> "event 1 ok".success[String]
res36: scalaz.Validation[String,String] = Success(event 1 ok)

scala> "event 1 failed!".failure[String]
res38: scalaz.Validation[String,String] = Failure(event 1 failed!)

Validation の違いはこれがモナドではなく、Applicative functor であることだ。最初のイベントの結果を次へと連鎖するのでは無く、Validation は全イベントを検証する:

scala> ("event 1 ok".success[String] |@| "event 2 failed!".failure[String] |@| "event 3 failed!".failure[String]) {_ + _ + _}
res44: scalaz.Unapply[scalaz.Apply,scalaz.Validation[String,String]]{type M[X] = scalaz.Validation[String,X]; type A = String}#M[String] = Failure(event 2 failed!event 3 failed!)

ちょっと読みづらいけど、最終結果は Failure(event 2 failed!event 3 failed!) だ。計算途中でショートさせた \/ と違って、Validation は計算を続行して全ての失敗を報告する。これはおそらくオンラインのベーコンショップでユーザのインプットを検証するのに役立つと思う。

だけど、問題はエラーメッセージが 1つの文字列にゴチャっと一塊になってしまっていることだ。リストでも使うべきじゃないか?

NonEmptyList

ここで NonEmptyList (略して Nel) が登場する:

/** A singly-linked list that is guaranteed to be non-empty. */
sealed trait NonEmptyList[+A] {
  val head: A
  val tail: List[A]
  def <::[AA >: A](b: AA): NonEmptyList[AA] = nel(b, head :: tail)
  ...
}

これは素の List のラッパーで、空じゃないことを保証する。必ず 1つのアイテムがあることで head は常に成功する。IdOps は Nel を作るために wrapNel を全てのデータ型に導入する。

scala> 1.wrapNel
res47: scalaz.NonEmptyList[Int] = NonEmptyList(1)

これで successNel[X] と failureNel[X] が分かったかな?

scala> "event 1 ok".successNel[String]
res48: scalaz.ValidationNEL[String,String] = Success(event 1 ok)

scala> "event 1 failed!".failureNel[String]
res49: scalaz.ValidationNEL[String,String] = Failure(NonEmptyList(event 1 failed!))

scala> ("event 1 ok".successNel[String] |@| "event 2 failed!".failureNel[String] |@| "event 3 failed!".failureNel[String]) {_ + _ + _}
res50: scalaz.Unapply[scalaz.Apply,scalaz.ValidationNEL[String,String]]{type M[X] = scalaz.ValidationNEL[String,X]; type A = String}#M[String] = Failure(NonEmptyList(event 2 failed!, event 3 failed!))

Failure の中に全ての失敗メッセージを集約することができた。

続きはまたあとで。

8日目

7日目は、Applicative Builder をみて、あと State モナド、\/ モナド、Validation もみた。

便利なモナディック関数特集

すごいHaskellたのしく学ぼう曰く:

この節では、モナド値を操作したり、モナド値を返したりする関数（両方でも可！）をいくつか紹介します。そんな関数はモナディック関数と呼ばれます。

Scalaz の Monad は Applicative を継承しているため、全てのモナドが Functor であることが保証される。そのため、map や <*> 演算子も使える。

join メソッド

LYAHFGG:

実は、任意の入れ子になったモナドは平らにできるんです。そして実は、これはモナド特有の性質なのです。このために、join という関数が用意されています。

Scalaz では join メソッド (およびシンボルを使ったエイリアス μ) は Bind によって導入される:

trait BindOps[F[_],A] extends Ops[F[A]] {
  ...
  def join[B](implicit ev: A <~< F[B]): F[B] = F.bind(self)(ev(_))
  def μ[B](implicit ev: A <~< F[B]): F[B] = F.bind(self)(ev(_))
  ...
}

使ってみよう:

scala> (Some(9.some): Option[Option[Int]]).join
res9: Option[Int] = Some(9)

scala> (Some(none): Option[Option[Int]]).join
res10: Option[Int] = None

scala> List(List(1, 2, 3), List(4, 5, 6)).join
res12: List[Int] = List(1, 2, 3, 4, 5, 6)

scala> 9.right[String].right[String].join
res15: scalaz.Unapply[scalaz.Bind,scalaz.\/[String,scalaz.\/[String,Int]]]{type M[X] = scalaz.\/[String,X]; type A = scalaz.\/[String,Int]}#M[Int] = \/-(9)

scala> "boom".left[Int].right[String].join
res16: scalaz.Unapply[scalaz.Bind,scalaz.\/[String,scalaz.\/[String,Int]]]{type M[X] = scalaz.\/[String,X]; type A = scalaz.\/[String,Int]}#M[Int] = -\/(boom)

filterM メソッド

LYAHFGG:

Control.Monad モジュールの filterM こそ、まさにそのための関数です！ … 述語は Bool を結果とするモナド値を返しています。

Scalaz では filterM はいくつかの箇所で実装されている。

trait ListOps[A] extends Ops[List[A]] {
  ...
  final def filterM[M[_] : Monad](p: A => M[Boolean]): M[List[A]] = l.filterM(self)(p)
  ...
}

scala> List(1, 2, 3) filterM { x => List(true, false) }
res19: List[List[Int]] = List(List(1, 2, 3), List(1, 2), List(1, 3), List(1), List(2, 3), List(2), List(3), List())

scala> Vector(1, 2, 3) filterM { x => Vector(true, false) }
res20: scala.collection.immutable.Vector[Vector[Int]] = Vector(Vector(1, 2, 3), Vector(1, 2), Vector(1, 3), Vector(1), Vector(2, 3), Vector(2), Vector(3), Vector())

foldLeftM メソッド

LYAHFGG:

foldl のモナド版が foldM です。

Scalaz でこれは Foldable に foldLeftM として実装されていて、foldRightM もある。

scala> def binSmalls(acc: Int, x: Int): Option[Int] = {
         if (x > 9) (none: Option[Int])
         else (acc + x).some
       }
binSmalls: (acc: Int, x: Int)Option[Int]

scala> List(2, 8, 3, 1).foldLeftM(0) {binSmalls}
res25: Option[Int] = Some(14)

scala> List(2, 11, 3, 1).foldLeftM(0) {binSmalls}
res26: Option[Int] = None

安全な RPN 電卓を作ろう

LYAHFGG:

第10章で逆ポーランド記法 (RPN) の電卓を実装せよという問題を解いたときには、この電卓は文法的に正しい入力が与えられる限り正しく動くよ、という注意書きがありました。

最初に RPN 電卓を作った章は飛ばしたけど、コードはここにあるから Scala に訳してみる:

scala> def foldingFunction(list: List[Double], next: String): List[Double] = (list, next) match {
         case (x :: y :: ys, "*") => (y * x) :: ys
         case (x :: y :: ys, "+") => (y + x) :: ys
         case (x :: y :: ys, "-") => (y - x) :: ys
         case (xs, numString) => numString.toInt :: xs
       }
foldingFunction: (list: List[Double], next: String)List[Double]

scala> def solveRPN(s: String): Double =
         (s.split(' ').toList.foldLeft(Nil: List[Double]) {foldingFunction}).head
solveRPN: (s: String)Double

scala> solveRPN("10 4 3 + 2 * -")
res27: Double = -4.0

動作しているみたいだ。次に畳み込み関数がエラーを処理できるようにする。Scalaz は String に Validation[NumberFormatException, Int] を返す parseInt を導入する。これに対して toOption を呼べば本の通り Option[Int] が得られる:

scala> "1".parseInt.toOption
res31: Option[Int] = Some(1)

scala> "foo".parseInt.toOption
res32: Option[Int] = None

以下が更新された畳込み関数:

scala> def foldingFunction(list: List[Double], next: String): Option[List[Double]] = (list, next) match {
         case (x :: y :: ys, "*") => ((y * x) :: ys).point[Option]
         case (x :: y :: ys, "+") => ((y + x) :: ys).point[Option]
         case (x :: y :: ys, "-") => ((y - x) :: ys).point[Option]
         case (xs, numString) => numString.parseInt.toOption map {_ :: xs}
       }
foldingFunction: (list: List[Double], next: String)Option[List[Double]]

scala> foldingFunction(List(3, 2), "*")
res33: Option[List[Double]] = Some(List(6.0))

scala> foldingFunction(Nil, "*")
res34: Option[List[Double]] = None

scala> foldingFunction(Nil, "wawa")
res35: Option[List[Double]] = None

以下が更新された solveRPN:

scala> def solveRPN(s: String): Option[Double] = for {
         List(x) <- s.split(' ').toList.foldLeftM(Nil: List[Double]) {foldingFunction}
       } yield x
solveRPN: (s: String)Option[Double]

scala> solveRPN("1 2 * 4 +")
res36: Option[Double] = Some(6.0)

scala> solveRPN("1 2 * 4")
res37: Option[Double] = None

scala> solveRPN("1 8 garbage")
res38: Option[Double] = None

モナディック関数の合成

LYAHFGG:

第13章でモナド則を紹介したとき、<=< 関数は関数合成によく似ているど、普通の関数 a -> b ではなくて、a -> m b みたいなモナディック関数に作用するのだよと言いました。

これも飛ばしてたみたいだ。

Kleisli

Scalaz には Kleisli と呼ばれる A => M[B] という型の関数に対する特殊なラッパーがある:

sealed trait Kleisli[M[+_], -A, +B] { self =>
  def run(a: A): M[B]
  ...
  /** alias for `andThen` */
  def >=>[C](k: Kleisli[M, B, C])(implicit b: Bind[M]): Kleisli[M, A, C] =  kleisli((a: A) => b.bind(this(a))(k(_)))
  def andThen[C](k: Kleisli[M, B, C])(implicit b: Bind[M]): Kleisli[M, A, C] = this >=> k
  /** alias for `compose` */ 
  def <=<[C](k: Kleisli[M, C, A])(implicit b: Bind[M]): Kleisli[M, C, B] = k >=> this
  def compose[C](k: Kleisli[M, C, A])(implicit b: Bind[M]): Kleisli[M, C, B] = k >=> this
  ...
}

object Kleisli extends KleisliFunctions with KleisliInstances {
  def apply[M[+_], A, B](f: A => M[B]): Kleisli[M, A, B] = kleisli(f)
}

構築するには Kleisli オブジェクトを使う:

scala> val f = Kleisli { (x: Int) => (x + 1).some }
f: scalaz.Kleisli[Option,Int,Int] = scalaz.KleisliFunctions$$anon$18@7da2734e

scala> val g = Kleisli { (x: Int) => (x * 100).some }
g: scalaz.Kleisli[Option,Int,Int] = scalaz.KleisliFunctions$$anon$18@49e07991

<=< を使って関数を合成すると、f compose g と同様に右辺項が先に適用される。

scala> 4.some >>= (f <=< g)
res59: Option[Int] = Some(401)

>=> を使うと、f andThen g 同様に左辺項が先に適用される:

scala> 4.some >>= (f >=> g)
res60: Option[Int] = Some(500)

Reader 再び

ボーナスとして、Scalaz は Reader を Kleisli の特殊形として以下のように定義する:

  type ReaderT[F[+_], E, A] = Kleisli[F, E, A]
  type Reader[E, A] = ReaderT[Id, E, A]
  object Reader {
    def apply[E, A](f: E => A): Reader[E, A] = Kleisli[Id, E, A](f)
  }

6日目のリーダーの例題は以下のように書き換えることができる:

scala> val addStuff: Reader[Int, Int] = for {
         a <- Reader { (_: Int) * 2 }
         b <- Reader { (_: Int) + 10 }
       } yield a + b
addStuff: scalaz.Reader[Int,Int] = scalaz.KleisliFunctions$$anon$18@343bd3ae

scala> addStuff(3)
res76: scalaz.Id.Id[Int] = 19

関数をモナドとして使っていることが少しかは明らかになったと思う。

モナドを作る

LYAHFGG:

この節では、型が生まれてモナドであると確認され、適切な Monad インスタンスが与えられるまでの過程を、例題を通して学ぼうと思います。 … [3,5,9] のような非決定的値を表現したいのだけど、さらに 3 である確率は 50パーセント、5 と 9 である確率はそれぞれ 25パーセントである、ということを表したくなったらどうしましょう？

Scala に有理数が標準で入っていないので、Double を使う。以下が case class:

scala> :paste
// Entering paste mode (ctrl-D to finish)

case class Prob[A](list: List[(A, Double)])

trait ProbInstances {
  implicit def probShow[A]: Show[Prob[A]] = Show.showA
}

case object Prob extends ProbInstances

// Exiting paste mode, now interpreting.

defined class Prob
defined trait ProbInstances
defined module Prob

これってファンクターでしょうか？ええ、リストはファンクターですから、リストに何かを足したものである Prob もたぶんファンクターでしょう。

scala> :paste
// Entering paste mode (ctrl-D to finish)

case class Prob[A](list: List[(A, Double)])

trait ProbInstances {
  implicit val probInstance = new Functor[Prob] {
    def map[A, B](fa: Prob[A])(f: A => B): Prob[B] =
      Prob(fa.list map { case (x, p) => (f(x), p) })
  }
  implicit def probShow[A]: Show[Prob[A]] = Show.showA
}

case object Prob extends ProbInstances

scala> Prob((3, 0.5) :: (5, 0.25) :: (9, 0.25) :: Nil) map {-_} 
res77: Prob[Int] = Prob(List((-3,0.5), (-5,0.25), (-9,0.25)))

本と同様に flatten をまず実装する。

case class Prob[A](list: List[(A, Double)])

trait ProbInstances {
  def flatten[B](xs: Prob[Prob[B]]): Prob[B] = {
    def multall(innerxs: Prob[B], p: Double) =
      innerxs.list map { case (x, r) => (x, p * r) }
    Prob((xs.list map { case (innerxs, p) => multall(innerxs, p) }).flatten)
  }

  implicit val probInstance = new Functor[Prob] {
    def map[A, B](fa: Prob[A])(f: A => B): Prob[B] =
      Prob(fa.list map { case (x, p) => (f(x), p) })
  }
  implicit def probShow[A]: Show[Prob[A]] = Show.showA
}

case object Prob extends ProbInstances

これでモナドのための準備は整ったはずだ:

scala> :paste
// Entering paste mode (ctrl-D to finish)

case class Prob[A](list: List[(A, Double)])

trait ProbInstances {
  def flatten[B](xs: Prob[Prob[B]]): Prob[B] = {
    def multall(innerxs: Prob[B], p: Double) =
      innerxs.list map { case (x, r) => (x, p * r) }
    Prob((xs.list map { case (innerxs, p) => multall(innerxs, p) }).flatten)
  }

  implicit val probInstance = new Functor[Prob] with Monad[Prob] {
    def point[A](a: => A): Prob[A] = Prob((a, 1.0) :: Nil)
    def bind[A, B](fa: Prob[A])(f: A => Prob[B]): Prob[B] = flatten(map(fa)(f)) 
    override def map[A, B](fa: Prob[A])(f: A => B): Prob[B] =
      Prob(fa.list map { case (x, p) => (f(x), p) })
  }
  implicit def probShow[A]: Show[Prob[A]] = Show.showA
}

case object Prob extends ProbInstances

// Exiting paste mode, now interpreting.

defined class Prob
defined trait ProbInstances
defined module Prob

本によるとモナド則は満たしているらしい。Coin の例題も実装してみよう:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait Coin
case object Heads extends Coin
case object Tails extends Coin
implicit val coinEqual: Equal[Coin] = Equal.equalA

def coin: Prob[Coin] = Prob(Heads -> 0.5 :: Tails -> 0.5 :: Nil)
def loadedCoin: Prob[Coin] = Prob(Heads -> 0.1 :: Tails -> 0.9 :: Nil)

def flipThree: Prob[Boolean] = for {
  a <- coin
  b <- coin
  c <- loadedCoin
} yield { List(a, b, c) all {_ === Tails} }

// Exiting paste mode, now interpreting.

defined trait Coin
defined module Heads
defined module Tails
coin: Prob[Coin]
loadedCoin: Prob[Coin]
flipThree: Prob[Boolean]

scala> flipThree
res81: Prob[Boolean] = Prob(List((false,0.025), (false,0.225), (false,0.025), (false,0.225), (false,0.025), (false,0.225), (false,0.025), (true,0.225)))

イカサマのコインを 1つ使っても 3回とも裏が出る確率はかなり低いことが分かった。

続きはまた後で。

9日目

8日目は、モナディック関数の join、filterM、と foldLeftM をみて、安全な RPN 電卓を実装して、Kleisli を使ってモナディック関数を合成する方法をみた後で、独自のモナド Prob を実装した。

Tree

すごいHaskellたのしく学ぼうの最終章 Zippers を始めよう:

この章では、いくつかのデータ構造に、そのデータ構造の一部分に注目するための Zipper を備える方法を紹介します。Zipper はデータ構造の要素の更新を簡単にし、データ構造を辿るという操作を効率的にしてくれるんです。

Scala の case class の等価性はヒープ内の位置じゃなくて内容で決まる。そのため、木構造内の複数のノードを識別するだけでももし偶然同じ型と内容があれば Scala は同じもの扱いしてしまう。

独自の木を実装するかわりに、Scalaz の Tree を使おう:

sealed trait Tree[A] {
  /** The label at the root of this tree. */
  def rootLabel: A
  /** The child nodes of this tree. */
  def subForest: Stream[Tree[A]]
}

object Tree extends TreeFunctions with TreeInstances {
  /** Construct a tree node with no children. */
  def apply[A](root: => A): Tree[A] = leaf(root)

  object Node {
    def unapply[A](t: Tree[A]): Option[(A, Stream[Tree[A]])] = Some((t.rootLabel, t.subForest))
  }
}

trait TreeFunctions {
  /** Construct a new Tree node. */
  def node[A](root: => A, forest: => Stream[Tree[A]]): Tree[A] = new Tree[A] {
    lazy val rootLabel = root
    lazy val subForest = forest
    override def toString = "<tree>"
  }
  /** Construct a tree node with no children. */
  def leaf[A](root: => A): Tree[A] = node(root, Stream.empty)
  ...
}

これは多分木 (multi-way tree) だ。木を作るためには全てのデータ型に注入された node メソッドと leaf メソッドを使う:

trait TreeV[A] extends Ops[A] {
  def node(subForest: Tree[A]*): Tree[A] = Tree.node(self, subForest.toStream)

  def leaf: Tree[A] = Tree.leaf(self)
}

本にある freeTree を実装してみる:

scala> def freeTree: Tree[Char] =
         'P'.node(
           'O'.node(
             'L'.node('N'.leaf, 'T'.leaf),
             'Y'.node('S'.leaf, 'A'.leaf)),
           'L'.node(
             'W'.node('C'.leaf, 'R'.leaf),
             'A'.node('A'.leaf, 'C'.leaf)))
freeTree: scalaz.Tree[Char]

LYAHFGG:

ほら、木の中に W が見えますか？あれを P に変えたいな。どうすればできるでしょう？

Tree.Node という抽出子があるので、changeToP は以下のように実装できる:

scala> def changeToP(tree: Tree[Char]): Tree[Char] = tree match {
         case Tree.Node(x, Stream(
           l, Tree.Node(y, Stream(
             Tree.Node(_, Stream(m, n)), r)))) =>
           x.node(l, y.node('P'.node(m, n), r))
       }
changeToP: (tree: scalaz.Tree[Char])scalaz.Tree[Char]

これを実装するのはかなり面倒だった。Zipper をみてみよう。

TreeLoc

LYAHFGG:

Tree a と Breadcrumbs a のペアは、元の木全体を復元するのに必要な情報に加えて、ある部分木に注目した状態というのを表現しています。このスキームなら、木の中を上、左、右へと自由自在に移動できます。あるデータ構造の注目点、および周辺の情報を含んでいるデータ構造は Zipper と呼ばれます。注目点をデータ構造に沿って上下させる操作は、ズボンのジッパーを上下させる操作に似ているからです。

Tree のための Zipper は Scalaz では TreeLoc と呼ばれている:

sealed trait TreeLoc[A] {
  import TreeLoc._
  import Tree._

  /** The currently selected node. */
  val tree: Tree[A]
  /** The left siblings of the current node. */
  val lefts: TreeForest[A]
  /** The right siblings of the current node. */
  val rights: TreeForest[A]
  /** The parent contexts of the current node. */
  val parents: Parents[A]
  ...
}

object TreeLoc extends TreeLocFunctions with TreeLocInstances {
  def apply[A](t: Tree[A], l: TreeForest[A], r: TreeForest[A], p: Parents[A]): TreeLoc[A] =
    loc(t, l, r, p)
}

trait TreeLocFunctions {
  type TreeForest[A] = Stream[Tree[A]]
  type Parent[A] = (TreeForest[A], A, TreeForest[A])
  type Parents[A] = Stream[Parent[A]]
}

Zipper のデータ構造は一般的に穴を表現する。現在フォーカスがあるノードは tree で表されているけど、木全体を再び構築するのに必要なその他全ても保存されている。TreeLoc を作るには Tree から loc メソッドを呼び出す:

scala> freeTree.loc
res0: scalaz.TreeLoc[Char] = scalaz.TreeLocFunctions$$anon$2@6439ca7b

TreeLoc はフォーカスを移動するのに DOM API のような様々なメソッドを実装する:

sealed trait TreeLoc[A] {
  ...
  /** Select the parent of the current node. */
  def parent: Option[TreeLoc[A]] = ...
  /** Select the root node of the tree. */
  def root: TreeLoc[A] = ...
  /** Select the left sibling of the current node. */
  def left: Option[TreeLoc[A]] = ...
  /** Select the right sibling of the current node. */
  def right: Option[TreeLoc[A]] = ...
  /** Select the leftmost child of the current node. */
  def firstChild: Option[TreeLoc[A]] = ...
  /** Select the rightmost child of the current node. */
  def lastChild: Option[TreeLoc[A]] = ...
  /** Select the nth child of the current node. */
  def getChild(n: Int): Option[TreeLoc[A]] = ...
  /** Select the first immediate child of the current node that satisfies the given predicate. */
  def findChild(p: Tree[A] => Boolean): Option[TreeLoc[A]] = ...
  /** Get the label of the current node. */
  def getLabel: A = ...
  ...
}

freeTree の W にフォーカスを移動するのは以下のように書ける:

scala> freeTree.loc.getChild(2) >>= {_.getChild(1)}
res8: Option[scalaz.TreeLoc[Char]] = Some(scalaz.TreeLocFunctions$$anon$2@417ef051)

scala> freeTree.loc.getChild(2) >>= {_.getChild(1)} >>= {_.getLabel.some}
res9: Option[Char] = Some(W)

getChild が Option[TreeLoc[A]] を返すためにモナディック連鎖の >>= を使っているけど、これは flatMap と同じことだ。getChild がちょっと変わっているのが 1-base の添字を使っていることだ。変更を加えて新しい TreeLoc を作るメソッドも色々あるけど、便利そうなのは以下のものだ:

  /** Modify the current node with the given function. */
  def modifyTree(f: Tree[A] => Tree[A]): TreeLoc[A] = ...
  /** Modify the label at the current node with the given function. */
  def modifyLabel(f: A => A): TreeLoc[A] = ...
  /** Insert the given node as the last child of the current node and give it focus. */
  def insertDownLast(t: Tree[A]): TreeLoc[A] = ...

ラベルを 'P' 変更してみよう:

scala> val newFocus = freeTree.loc.getChild(2) >>= {_.getChild(1)} >>= {_.modifyLabel({_ => 'P'}).some}
newFocus: Option[scalaz.TreeLoc[Char]] = Some(scalaz.TreeLocFunctions$$anon$2@107a26d0)

newFocus から木を再構築するには toTree メソッドを呼ぶだけでいい:

scala> newFocus.get.toTree
res19: scalaz.Tree[Char] = <tree>

scala> newFocus.get.toTree.draw foreach {_.print}
P|O+- ||  L+- |  ||  |  N+- |  |  ||  |  T`- |  |  ||  Y`- |  |   |  S+-    |  |   |  A`-    |  |L`- |   P+-    ||     C+- |     ||     R`- |     |   A`-    |      A+-       |      C`-

木の中身を検証するのに Tree の draw があるみたいだけど、改行を入れても入れなくても変な表示になった。

Zipper

LYAHFGG:

ジッパーは、ほぼどんなデータ型に対しても作れるので、リストと部分リストに対して作れるといっても不思議ではないでしょう。

リストの Zipper のかわりに、Scalaz は Stream 向けのものを提供する。Haskell の遅延評価のため、Scala の Stream を Haskell のリストを考えるのは理にかなっているのかもしれない。これが Zipper だ:

sealed trait Zipper[+A] {
  val focus: A
  val lefts: Stream[A]
  val rights: Stream[A]
  ...
}

Zipper を作るには Stream に注入された toZipper か zipperEnd メソッドを使う:

trait StreamOps[A] extends Ops[Stream[A]] {
  final def toZipper: Option[Zipper[A]] = s.toZipper(self)
  final def zipperEnd: Option[Zipper[A]] = s.zipperEnd(self)
  ...
}

使ってみる:

scala> Stream(1, 2, 3, 4)
res23: scala.collection.immutable.Stream[Int] = Stream(1, ?)

scala> Stream(1, 2, 3, 4).toZipper
res24: Option[scalaz.Zipper[Int]] = Some(Zipper(<lefts>, 1, <rights>))

TreeLoc 同様に Zipper にも移動のために多くのメソッドが用意されてある:

sealed trait Zipper[+A] {
  ...
  /** Possibly moves to next element to the right of focus. */
  def next: Option[Zipper[A]] = ...
  def nextOr[AA >: A](z: => Zipper[AA]): Zipper[AA] = next getOrElse z
  def tryNext: Zipper[A] = nextOr(sys.error("cannot move to next element"))
  /** Possibly moves to the previous element to the left of focus. */
  def previous: Option[Zipper[A]] = ...
  def previousOr[AA >: A](z: => Zipper[AA]): Zipper[AA] = previous getOrElse z
  def tryPrevious: Zipper[A] = previousOr(sys.error("cannot move to previous element"))
  /** Moves focus n elements in the zipper, or None if there is no such element. */
  def move(n: Int): Option[Zipper[A]] = ...
  def findNext(p: A => Boolean): Option[Zipper[A]] = ...
  def findPrevious(p: A => Boolean): Option[Zipper[A]] = ...
  
  def modify[AA >: A](f: A => AA) = ...
  def toStream: Stream[A] = ...
  ...
}

使ってみるとこうなる:

scala> Stream(1, 2, 3, 4).toZipper >>= {_.next}
res25: Option[scalaz.Zipper[Int]] = Some(Zipper(<lefts>, 2, <rights>))

scala> Stream(1, 2, 3, 4).toZipper >>= {_.next} >>= {_.next}
res26: Option[scalaz.Zipper[Int]] = Some(Zipper(<lefts>, 3, <rights>))

scala> Stream(1, 2, 3, 4).toZipper >>= {_.next} >>= {_.next} >>= {_.previous}
res27: Option[scalaz.Zipper[Int]] = Some(Zipper(<lefts>, 2, <rights>))

現在のフォーカスを変更して Stream に戻すには modify と toStream メソッドを使う:

scala> Stream(1, 2, 3, 4).toZipper >>= {_.next} >>= {_.next} >>= {_.modify {_ => 7}.some}
res31: Option[scalaz.Zipper[Int]] = Some(Zipper(<lefts>, 7, <rights>))

scala> res31.get.toStream.toList
res32: List[Int] = List(1, 2, 7, 4)

これは for 構文を使って書くこともできる:

scala> for {
         z <- Stream(1, 2, 3, 4).toZipper
         n1 <- z.next
         n2 <- n1.next
       } yield { n2.modify {_ => 7} }
res33: Option[scalaz.Zipper[Int]] = Some(Zipper(<lefts>, 7, <rights>))

読みやすいとは思うけど、何行も使うから場合によりけりだと思う。

すごいHaskellたのしく学ぼう (Learn You a Haskell for Great Good) はひとまずこれでおしまい。Scalaz が提供する全てのものはカバーしなかったけど、基礎からゆっくりと入っていくのにとても良い本だったと思う。Haskell に対応する型を探しているうちに Scalaz のソースを読む勘がついてきたので、あとは色々調べながらでもいけそうだ。

とりあえず、紹介する機会を逸した型クラスがいくつかあるので紹介したい。

Id

Hoogle を使って Haskell の型クラスを調べることができる。例えば、Control.Monad.Identity をみてみよう:

The Identity monad is a monad that does not embody any computational strategy. It simply applies the bound function to its input without any modification. Computationally, there is no reason to use the Identity monad instead of the much simpler act of simply applying functions to their arguments. The purpose of the Identity monad is its fundamental role in the theory of monad transformers. Any monad transformer applied to the Identity monad yields a non-transformer version of that monad.

Scalaz に対応する型はこれだ:

  /** The strict identity type constructor. Can be thought of as `Tuple1`, but with no
   *  runtime representation.
   */
  type Id[+X] = X

モナド変換子は後回しにするとして、面白いのは全てのデータ型はその型の Id となれることだ:

scala> (0: Id[Int])
res39: scalaz.Scalaz.Id[Int] = 0

Scalaz はこの Id 経由でいくつかの便利なメソッドを導入する:

trait IdOps[A] extends Ops[A] {
  /**Returns `self` if it is non-null, otherwise returns `d`. */
  final def ??(d: => A)(implicit ev: Null <:< A): A =
    if (self == null) d else self
  /**Applies `self` to the provided function */
  final def |>[B](f: A => B): B = f(self)
  final def squared: (A, A) = (self, self)
  def left[B]: (A \/ B) = \/.left(self)
  def right[B]: (B \/ A) = \/.right(self)
  final def wrapNel: NonEmptyList[A] = NonEmptyList(self)
  /** @return the result of pf(value) if defined, otherwise the the Zero element of type B. */
  def matchOrZero[B: Monoid](pf: PartialFunction[A, B]): B = ...
  /** Repeatedly apply `f`, seeded with `self`, checking after each iteration whether the predicate `p` holds. */
  final def doWhile(f: A => A, p: A => Boolean): A = ...
  /** Repeatedly apply `f`, seeded with `self`, checking before each iteration whether the predicate `p` holds. */
  final def whileDo(f: A => A, p: A => Boolean): A = ...
  /** If the provided partial function is defined for `self` run this,
   * otherwise lift `self` into `F` with the provided [[scalaz.Pointed]]. */
  def visit[F[_] : Pointed](p: PartialFunction[A, F[A]]): F[A] = ...
}

|> で式の後に関数の適用を書くことができる:

scala> 1 + 2 + 3 |> {_.point[List]}
res45: List[Int] = List(6)

scala> 1 + 2 + 3 |> {_ * 6}
res46: Int = 36

visit も興味深い:

scala> 1 visit { case x@(2|3) => List(x * 2) }
res55: List[Int] = List(1)

scala> 2 visit { case x@(2|3) => List(x * 2) }
res56: List[Int] = List(4)

無法者の型クラス

Scalaz 7.0 は、今の Scalaz プロジェクトの考えでは無法 (lawless) だと烙印を押された型クラス Length、Index、Each を含む。これらに関する議論は #278 What to do about lawless classes? や (presumably) Bug in IndexedSeq Index typeclass を参照。それらの型クラスは 7.1 で廃止予定 (deprecated) 扱いされ、7.2 では削除される予定だ。

Length

長さを表現した型クラス。以下が Length 型クラスのコントラクトだ:

trait Length[F[_]]  { self =>
  def length[A](fa: F[A]): Int
}

これは length メソッドを導入する。Scala 標準ライブラリだと SeqLike で入ってくるため、SeqLike を継承しないけど長さを持つデータ構造があれば役に立つのかもしれない。

Index

コンテナへのランダムアクセスを表すのが Index だ:

trait Index[F[_]]  { self =>
  def index[A](fa: F[A], i: Int): Option[A]
}

これは index と indexOr メソッドを導入する:

trait IndexOps[F[_],A] extends Ops[F[A]] {
  final def index(n: Int): Option[A] = F.index(self, n)
  final def indexOr(default: => A, n: Int): A = F.indexOr(self, default, n)
}

これは List(n) に似ているけど、範囲外の添字で呼び出すと None が返る:

scala> List(1, 2, 3)(3)
java.lang.IndexOutOfBoundsException: 3
        ...

scala> List(1, 2, 3) index 3
res62: Option[Int] = None

Each

データ構造を走査して副作用のある関数を実行するために Each がある:

trait Each[F[_]]  { self =>
  def each[A](fa: F[A])(f: A => Unit)
}

これは foreach メソッドを導入する:

sealed abstract class EachOps[F[_],A] extends Ops[F[A]] {
  final def foreach(f: A => Unit): Unit = F.each(self)(f)
}

Foldable かオレオレ型クラスを書くか?

上に挙げた機能のいくつかは Foldable を使ってエミュレートすることができるけども、@nuttycom氏が指摘するように、それでは対象となるデータ構造が定数時間の length や index を実装していたとしても O(n) 時間を強要することになる。仮に length を抽象化して役に立つとした場合、恐らく自分で Length を書いてしまった方がいいだろう。

もし、一貫性に欠ける型クラスの実装が何らかの形で型安全性を劣化させているならライブラリから削除するのも止むを得ないと思うが、一見して Length や Index は Vector などのランダムアクセス可能なコンテナに対する合理的な抽象化のように見える。

Pointed と Copointed

実は以前にも無法であるとして斬られた型クラスがあって Pointed と Copointed がそれだ。これに関しては参考になる議論が Pointed/Copointed や Why not Pointed? にある:

Pointed は有用な法則を持たないし、皆が教えてくれる利用方法のほとんどが実際にはインスタンスそのものが提供している関係を ad hoc に乱用したものであることが多い。

これは興味深い指摘で、僕にも理解できるものだ。別の言い方をすると、もしどんなコンテナでも Pointed になることができるなら、それを使っているコードはあまり役に立たないものか、もしくはそれが何らかの特定のインスタンスであると暗に仮定したものではないかということだ。

読者の声

@eed3si9n "axiomatic" would be better.
— Miles Sabin (@milessabin) December 29, 2013

@eed3si9n Foldable too (unless it also has a Functor but then nothing past parametricity): https://t.co/Lp0YkUTRD9 - but Reducer has laws!
— Brian McKenna (@puffnfresh) December 29, 2013

10日目

9日目は TreeLoc や Zipper を使った不変データ構造の更新する方法をみた。また、Id、Index、Length などの型クラスもみた。Learn You a Haskell for Great Good を終えてしまったので、今後は自分でトピックを考えなければいけない。

Scalaz 7 で何度も見て気になっている概念にモナド変換子というのがあるので、何なのかみてみる。幸いなことに、Haskell の良書でオンライン版も公開されている本がもう 1冊ある。

モナド変換子

Real World Haskell―実戦で学ぶ関数型言語プログラミングの原書の Real World Haskell 曰く:

It would be ideal if we could somehow take the standard State monad and add failure handling to it, without resorting to the wholesale construction of custom monads by hand. The standard monads in the mtl library don’t allow us to combine them. Instead, the library provides a set of monad transformers to achieve the same result.
A monad transformer is similar to a regular monad, but it’s not a standalone entity: instead, it modifies the behaviour of an underlying monad.

Reader、再三

Reader モナドの例を Scala にまず翻訳してみる:

scala> def myName(step: String): Reader[String, String] = Reader {step + ", I am " + _}
myName: (step: String)scalaz.Reader[String,String]

scala> def localExample: Reader[String, (String, String, String)] = for {
         a <- myName("First")
         b <- myName("Second") >=> Reader { _ + "dy"}
         c <- myName("Third")  
       } yield (a, b, c)
localExample: scalaz.Reader[String,(String, String, String)]

scala> localExample("Fred")
res0: (String, String, String) = (First, I am Fred,Second, I am Freddy,Third, I am Fred)

Reader のポイントはコンフィギュレーション情報を一度渡せばあとは明示的に渡して回さなくても皆が使うことができることにある。Tony Morris さん(@dibblego) の Configuration Without the Bugs and Gymnastics 参照。

ReaderT

Reader のモナド変換子版である ReaderT を Option モナドの上に積んでみる。

scala> :paste
// Entering paste mode (ctrl-D to finish)

type ReaderTOption[A, B] = ReaderT[Option, A, B]
object ReaderTOption extends KleisliInstances with KleisliFunctions {
  def apply[A, B](f: A => Option[B]): ReaderTOption[A, B] = kleisli(f)
}

// Exiting paste mode, now interpreting.

ReaderTOption object を使って ReaderTOption 作れる:

scala> def configure(key: String) = ReaderTOption[Map[String, String], String] {_.get(key)} 
configure: (key: String)ReaderTOption[Map[String,String],String]

2日目に Function1 を無限の投射として考えるみたいな事を言ったけど、これは Map[String, String] をリーダーとして使うから逆をやっていることになる。

scala> def setupConnection = for {
         host <- configure("host")
         user <- configure("user")
         password <- configure("password")
       } yield (host, user, password)
setupConnection: scalaz.Kleisli[Option,Map[String,String],(String, String, String)]

scala> val goodConfig = Map(
         "host" -> "eed3si9n.com",
         "user" -> "sa",
         "password" -> "****"
       )
goodConfig: scala.collection.immutable.Map[String,String] = Map(host -> eed3si9n.com, user -> sa, password -> ****)

scala> setupConnection(goodConfig)
res2: Option[(String, String, String)] = Some((eed3si9n.com,sa,****))

scala> val badConfig = Map(
         "host" -> "example.com",
         "user" -> "sa"
       )
badConfig: scala.collection.immutable.Map[String,String] = Map(host -> example.com, user -> sa)

scala> setupConnection(badConfig)
res3: Option[(String, String, String)] = None

見ての通り、ReaderTOption モナドは Reader の能力であるコンフィギュレーションを一回読むことと、Option の能力である失敗の表現を併せ持っている。

複数のモナド変換子を積み上げる

RWH:

When we stack a monad transformer on a normal monad, the result is another monad. This suggests the possibility that we can again stack a monad transformer on top of our combined monad, to give a new monad, and in fact this is a common thing to do.

状態遷移を表す StateT を ReaderTOption の上に積んでみる。

scala> :paste
// Entering paste mode (ctrl-D to finish)

type StateTReaderTOption[C, S, A] = StateT[({type l[X] = ReaderTOption[C, X]})#l, S, A]

object StateTReaderTOption extends StateTInstances with StateTFunctions {
  def apply[C, S, A](f: S => (S, A)) = new StateT[({type l[X] = ReaderTOption[C, X]})#l, S, A] {
    def apply(s: S) = f(s).point[({type l[X] = ReaderTOption[C, X]})#l]
  }
  def get[C, S]: StateTReaderTOption[C, S, S] =
    StateTReaderTOption { s => (s, s) }
  def put[C, S](s: S): StateTReaderTOption[C, S, Unit] =
    StateTReaderTOption { _ => (s, ()) }
}

// Exiting paste mode, now interpreting.

これは分かりづらい。結局の所 State モナドは S => (S, A) をラッピングするものだから、パラメータ名はそれに合わせた。次に、ReaderTOption のカインドを * -> * (ただ 1つのパラメータを受け取る型コンストラクタ) に変える。

7日目でみた State を使った Stack を実装しよう。

scala> type Stack = List[Int]
defined type alias Stack

scala> type Config = Map[String, String]
defined type alias Config

scala> val pop = StateTReaderTOption[Config, Stack, Int] {
         case x :: xs => (xs, x)
       }
pop: scalaz.StateT[[+X]scalaz.Kleisli[Option,Config,X],Stack,Int] = StateTReaderTOption$$anon$1@122313eb

get と put も書いたので、for 構文で書きなおすことができる:

scala> val pop: StateTReaderTOption[Config, Stack, Int] = {
         import StateTReaderTOption.{get, put}
         for {
           s <- get[Config, Stack]
           val (x :: xs) = s
           _ <- put(xs)
         } yield x
       }
pop: StateTReaderTOption[Config,Stack,Int] = scalaz.StateT$$anon$7@7eb316d2

これが push:

scala> def push(x: Int): StateTReaderTOption[Config, Stack, Unit] = {
         import StateTReaderTOption.{get, put}
         for {
           xs <- get[Config, Stack]
           r <- put(x :: xs)
         } yield r
       }
push: (x: Int)StateTReaderTOption[Config,Stack,Unit]

ついでに stackManip も移植する:

scala> def stackManip: StateTReaderTOption[Config, Stack, Int] = for {
         _ <- push(3)
         a <- pop
         b <- pop
       } yield(b)
stackManip: StateTReaderTOption[Config,Stack,Int]

実行してみよう。

scala> stackManip(List(5, 8, 2, 1))(Map())
res12: Option[(Stack, Int)] = Some((List(8, 2, 1),5))

とりあえず State 版と同じ機能までたどりつけた。configure を変更する:

scala> def configure[S](key: String) = new StateTReaderTOption[Config, S, String] {
         def apply(s: S) = ReaderTOption[Config, (S, String)] { config: Config => config.get(key) map {(s, _)} }
       }
configure: [S](key: String)StateTReaderTOption[Config,S,String]

これを使ってリードオンリーのコンフィギュレーションを使ったスタックの操作ができるようになった:

scala> def stackManip: StateTReaderTOption[Config, Stack, Unit] = for {
         x <- configure("x")
         a <- push(x.toInt)
       } yield(a)

scala> stackManip(List(5, 8, 2, 1))(Map("x" -> "7"))
res21: Option[(Stack, Unit)] = Some((List(7, 5, 8, 2, 1),()))

scala> stackManip(List(5, 8, 2, 1))(Map("y" -> "7"))
res22: Option[(Stack, Unit)] = None

これで StateT、ReaderT、それと Option を同時に動かすことができた。僕が使い方を良く分かってないせいだと思うけど、StateTReaderTOption と configure を定義して前準備をするのがかなり面倒だった。使う側のコード (stackManip) はクリーンだから、お正月などの特別な機会があったら使ってみたい。

LYAHFGG 無しで前途多難な感じのスタートとなったけど、続きはまた後で。

11日目

昨日はコンフィギュレーションを抽象化する方法として Reader をみた後、モナド変換子を紹介した。

Darren Hester for openphoto.net

今日はレンズを見てみよう。色んな人がレンズの話をして盛り上がってきてるトピックだし、使われるシナリオもはっきりしてるみたいだ。

Lens

今年の Scalathon で Seth Tisue さん (@SethTisue) が shapeless の Lens の話をした。残念ながら僕は聞けなかったけど、使われている例は借りさせてもらう。

scala> case class Point(x: Double, y: Double)
defined class Point

scala> case class Color(r: Byte, g: Byte, b: Byte)
defined class Color

scala> case class Turtle(
         position: Point,
         heading: Double,
         color: Color)

scala> Turtle(Point(2.0, 3.0), 0.0,
         Color(255.toByte, 255.toByte, 255.toByte))
res0: Turtle = Turtle(Point(2.0,3.0),0.0,Color(-1,-1,-1))

ここで不変性を壊さずに亀を前進させたい。

scala> case class Turtle(position: Point, heading: Double, color: Color) {
         def forward(dist: Double): Turtle =
           copy(position =
             position.copy(
               x = position.x + dist * math.cos(heading),
               y = position.y + dist * math.sin(heading)
           ))
       }
defined class Turtle

scala> Turtle(Point(2.0, 3.0), 0.0,
         Color(255.toByte, 255.toByte, 255.toByte))
res10: Turtle = Turtle(Point(2.0,3.0),0.0,Color(-1,-1,-1))

scala> res10.forward(10)
res11: Turtle = Turtle(Point(12.0,3.0),0.0,Color(-1,-1,-1))

中に入ったデータ構造を更新するには入れ子で copy を呼ばなくてはいけない。Seth 氏の話からまた借りると:

// 命令型
a.b.c.d.e += 1

// 関数型
a.copy(
  b = a.b.copy(
    c = a.b.c.copy(
      d = a.b.c.d.copy(
        e = a.b.c.d.e + 1
))))

この余計な copy の呼び出しを何とかしたい。

Scalaz 7 の Lens をみてみる:

  type Lens[A, B] = LensT[Id, A, B]

  object Lens extends LensTFunctions with LensTInstances {
    def apply[A, B](r: A => Store[B, A]): Lens[A, B] =
      lens(r)
  }

他の多くの型クラス同様 Lens は LensT[Id, A, B] の型エイリアスだ。

LensT

LensT はこうなっている:

import StoreT._
import Id._

sealed trait LensT[F[+_], A, B] {
  def run(a: A): F[Store[B, A]]
  def apply(a: A): F[Store[B, A]] = run(a)
  ...
}

object LensT extends LensTFunctions with LensTInstances {
  def apply[F[+_], A, B](r: A => F[Store[B, A]]): LensT[F, A, B] =
    lensT(r)
}

trait LensTFunctions {
  import StoreT._

  def lensT[F[+_], A, B](r: A => F[Store[B, A]]): LensT[F, A, B] = new LensT[F, A, B] {
    def run(a: A): F[Store[B, A]] = r(a)
  }

  def lensgT[F[+_], A, B](set: A => F[B => A], get: A => F[B])(implicit M: Bind[F]): LensT[F, A, B] =
    lensT(a => M(set(a), get(a))(Store(_, _)))
  def lensg[A, B](set: A => B => A, get: A => B): Lens[A, B] =
    lensgT[Id, A, B](set, get)
  def lensu[A, B](set: (A, B) => A, get: A => B): Lens[A, B] =
    lensg(set.curried, get)
  ...
}

Store

Store って何だろう?

  type Store[A, B] = StoreT[Id, A, B]
  // flipped
  type |-->[A, B] = Store[B, A]
  object Store {
    def apply[A, B](f: A => B, a: A): Store[A, B] = StoreT.store(a)(f)
  }

とりあえず setter (A => B => A) と getter (A => B) のラッパーらしい。

Lens を使う

turtlePosition と pointX を定義してみよう:

scala> val turtlePosition = Lens.lensu[Turtle, Point] (
         (a, value) => a.copy(position = value),
         _.position
       )
turtlePosition: scalaz.Lens[Turtle,Point] = scalaz.LensTFunctions$$anon$5@421dc8c8

scala> val pointX = Lens.lensu[Point, Double] (
         (a, value) => a.copy(x = value),
         _.x
       )
pointX: scalaz.Lens[Point,Double] = scalaz.LensTFunctions$$anon$5@30d31cf9

次に Lens で導入される演算子を利用することができる。Kleisli でみたモナディック関数の合成同様に、LensT も compose (シンボルを使ったエイリアスは <=<) と andThen (シンボルを使ったエイリアスは >=>) を実装する。個人的には >=> の見た目が良いと思うので、これを使って turtleX を定義する:

scala> val turtleX = turtlePosition >=> pointX
turtleX: scalaz.LensT[scalaz.Id.Id,Turtle,Double] = scalaz.LensTFunctions$$anon$5@11b35365

Turtle から Double に向かっているわけだから、型は理にかなっている。get メソッドを使って値を取得できる:

scala> val t0 = Turtle(Point(2.0, 3.0), 0.0,
                  Color(255.toByte, 255.toByte, 255.toByte))
t0: Turtle = Turtle(Point(2.0,3.0),0.0,Color(-1,-1,-1))

scala> turtleX.get(t0)
res16: scalaz.Id.Id[Double] = 2.0

成功だ! set メソッドを使って新たな値を設定すると新たな Turtle が返ってくる:

scala> turtleX.set(t0, 5.0)
res17: scalaz.Id.Id[Turtle] = Turtle(Point(5.0,3.0),0.0,Color(-1,-1,-1))

これもうまくいった。値を get して、なんらかの関数に適用した後、結果を set したい場合はどうすればいいだろう? mod がそれを行う:

scala> turtleX.mod(_ + 1.0, t0)
res19: scalaz.Id.Id[Turtle] = Turtle(Point(3.0,3.0),0.0,Color(-1,-1,-1))

mod のシンボルを使ったカリー化版として =>= がある。これは Turtle => Turtle 関数を生成する:

scala> val incX = turtleX =>= {_ + 1.0}
incX: Turtle => scalaz.Id.Id[Turtle] = <function1>

scala> incX(t0)
res26: scalaz.Id.Id[Turtle] = Turtle(Point(3.0,3.0),0.0,Color(-1,-1,-1))

これで内部値の変化を事前に記述して、最後に実際の値を渡すことができた。これは何かに似てない?

State モナドとしての Lens

これは状態遷移だと思う。実際、Lens と State は両方とも不変データ構造を使いながら命令形プログラミングを真似ているし相性がいいと思う。incX をこう書くこともできる:

scala> val incX = for {
         x <- turtleX %= {_ + 1.0}
       } yield x
incX: scalaz.StateT[scalaz.Id.Id,Turtle,Double] = scalaz.StateT$$anon$7@38e61ffa

scala> incX(t0)
res28: (Turtle, Double) = (Turtle(Point(3.0,3.0),0.0,Color(-1,-1,-1)),3.0)

%= メソッドは Double => Double 関数を受け取って、その変化を表す State モナドを返す。

turtleHeading と turtleY も作ろう:

scala> val turtleHeading = Lens.lensu[Turtle, Double] (
         (a, value) => a.copy(heading = value),
         _.heading
       )
turtleHeading: scalaz.Lens[Turtle,Double] = scalaz.LensTFunctions$$anon$5@44fdec57

scala> val pointY = Lens.lensu[Point, Double] (
         (a, value) => a.copy(y = value),
         _.y
       )
pointY: scalaz.Lens[Point,Double] = scalaz.LensTFunctions$$anon$5@ddede8c

scala> val turtleY = turtlePosition >=> pointY

これはボイラープレートっぽいので嬉しくない。だけど、これで亀を前進できる! 一般的な %= の代わりに、Scalaz は Numeric な Lens に対して += などの糖衣構文も提供する。具体例で説明する:

scala> def forward(dist: Double) = for {
         heading <- turtleHeading
         x <- turtleX += dist * math.cos(heading)
         y <- turtleY += dist * math.sin(heading)
       } yield (x, y)
forward: (dist: Double)scalaz.StateT[scalaz.Id.Id,Turtle,(Double, Double)]

scala> forward(10.0)(t0)
res31: (Turtle, (Double, Double)) = (Turtle(Point(12.0,3.0),0.0,Color(-1,-1,-1)),(12.0,3.0))

scala> forward(10.0) exec (t0)
res32: scalaz.Id.Id[Turtle] = Turtle(Point(12.0,3.0),0.0,Color(-1,-1,-1))

これで copy(position = ...) を一回も使わずに forward 関数を実装できた。これは便利だけど、ここまで来るのに準備も色々必要だったから、それはトレードオフだと言える。Lens は他にも多くのメソッドを定義するけど以上で十分使い始められると思う。並べて見てみる:

sealed trait LensT[F[+_], A, B] {
  def get(a: A)(implicit F: Functor[F]): F[B] =
    F.map(run(a))(_.pos)
  def set(a: A, b: B)(implicit F: Functor[F]): F[A] =
    F.map(run(a))(_.put(b))
  /** Modify the value viewed through the lens */
  def mod(f: B => B, a: A)(implicit F: Functor[F]): F[A] = ...
  def =>=(f: B => B)(implicit F: Functor[F]): A => F[A] =
    mod(f, _)
  /** Modify the portion of the state viewed through the lens and return its new value. */
  def %=(f: B => B)(implicit F: Functor[F]): StateT[F, A, B] =
    mods(f)
  /** Lenses can be composed */
  def compose[C](that: LensT[F, C, A])(implicit F: Bind[F]): LensT[F, C, B] = ...
  /** alias for `compose` */
  def <=<[C](that: LensT[F, C, A])(implicit F: Bind[F]): LensT[F, C, B] = compose(that)
  def andThen[C](that: LensT[F, B, C])(implicit F: Bind[F]): LensT[F, A, C] =
    that compose this
  /** alias for `andThen` */
  def >=>[C](that: LensT[F, B, C])(implicit F: Bind[F]): LensT[F, A, C] = andThen(that)
}

Lens 則

Seth さん曰く:

Lens 則は常識的な感覚
(0. 2度 get しても、同じ答が得られる) 1. get して、それを set しても何も変わらない。 2. set して、それを get すると、set したものが得られる。 3. 2度 set して、get すると、2度目に set したものが得られる。

確かに。常識的な感覚だ。Scalaz はコードでこれを表現する:

  trait LensLaw {
    def identity(a: A)(implicit A: Equal[A], ev: F[Store[B, A]] =:= Id[Store[B, A]]): Boolean = {
      val c = run(a)
      A.equal(c.put(c.pos), a)
    }
    def retention(a: A, b: B)(implicit B: Equal[B], ev: F[Store[B, A]] =:= Id[Store[B, A]]): Boolean =
      B.equal(run(run(a) put b).pos, b)
    def doubleSet(a: A, b1: B, b2: B)(implicit A: Equal[A], ev: F[Store[B, A]] =:= Id[Store[B, A]]) = {
      val r = run(a)
      A.equal(run(r put b1) put b2, r put b2)
    }
  }

任意の亀を定義すれば turtleX が大丈夫かチェックできる。これは省くけど、Lens 則を破るような変な Lens はくれぐれも作らないように。

リンク

Jordan West さんによる An Introduction to Lenses in Scalaz という記事があって、飛ばし読みした感じだと Scalaz 6 っぽい。

Edward Kmett さんが Boston Area Scala Enthusiasts (BASE) で発表した Lenses: A Functional Imperative のビデオもある。

最後に、Gerolf Seitz さんによる Lens を生成するコンパイラプラグイン gseitz/Lensed がある。このプロジェクトはまだ実験段階みたいだけど、手で書くかわりにマクロとかコンパイラが Lens を生成してくれる可能性を示している。

また続きは後で。

12日目

11日目には入れ子になった不変データ構造へのアクセスする方法を抽象化したものとしての Lens をみた。

reynaldo f. tamayo for openphoto.net

今日は論文をいくつか飛ばし読みしてみよう。まずは Jeremy Gibbons さんの Origami programming だ。

Origami programming

Gibbons さん曰く:

In this chapter we will look at folds and unfolds as abstractions. In a precise technical sense, folds and unfolds are the natural patterns of computation over recursive datatypes; unfolds generate data structures and folds consume them.

foldLeft は 4日目に Foldable を使ったときにみたけど、unfold って何だろう?

The dual of folding is unfolding. The Haskell standard List library deﬁnes the function unfoldr for generating lists.

Hoogle には以下の例がある:

Prelude Data.List> unfoldr (\b -> if b == 0 then Nothing else Just (b, b-1)) 10
[10,9,8,7,6,5,4,3,2,1]

DList

DList というデータ構造があって、それは DList.unfoldr をサポートする。DList もしくは差分リスト (difference list) は定数時間での追加をサポートするデータ構造だ。

scala> DList.unfoldr(10, { (x: Int) => if (x == 0) none else (x, x - 1).some })
res50: scalaz.DList[Int] = scalaz.DListFunctions$$anon$3@70627153

scala> res50.toList
res51: List[Int] = List(10, 9, 8, 7, 6, 5, 4, 3, 2, 1)

Stream の畳込み

Scalaz では StreamFunctions で定義されている unfold が import Scalaz._ で導入される:

scala> unfold(10) { (x) => if (x == 0) none else (x, x - 1).some }
res36: Stream[Int] = Stream(10, ?)

scala> res36.toList
res37: List[Int] = List(10, 9, 8, 7, 6, 5, 4, 3, 2, 1)

論文にある選択ソートの例を実装してみる:

scala> def minimumS[A: Order](stream: Stream[A]) = stream match {
         case x #:: xs => xs.foldLeft(x) {_ min _}
       }
minimumS: [A](stream: Stream[A])(implicit evidence$1: scalaz.Order[A])A

scala> def deleteS[A: Equal](y: A, stream: Stream[A]): Stream[A] = (y, stream) match {
         case (_, Stream()) => Stream()
         case (y, x #:: xs) =>
           if (y === x) xs
           else x #:: deleteS(y, xs) 
       }
deleteS: [A](y: A, stream: Stream[A])(implicit evidence$1: scalaz.Equal[A])Stream[A]

scala> def delmin[A: Order](stream: Stream[A]): Option[(A, Stream[A])] = stream match {
         case Stream() => none
         case xs =>
           val y = minimumS(xs)
           (y, deleteS(y, xs)).some
       }
delmin: [A](stream: Stream[A])(implicit evidence$1: scalaz.Order[A])Option[(A, Stream[A])]

scala> def ssort[A: Order](stream: Stream[A]): Stream[A] = unfold(stream){delmin[A]}
ssort: [A](stream: Stream[A])(implicit evidence$1: scalaz.Order[A])Stream[A]

scala> ssort(Stream(1, 3, 4, 2)).toList
res55: List[Int] = List(1, 2, 3, 4)

これは foldLeft と unfold を使っているからおりがみ (origami) プログラミングということなんだろうか? これは The Fun of Programming (邦訳は関数プログラミングの楽しみ) の 1章として 2003年に書かれたけど、おりがみプログラミングがその後流行ったかどうかは僕は知らない。

The Essence of the Iterator Pattern

2006年に同じ著者は、The Essence of the Iterator Pattern を発表した。リンクしたのは改訂された 2009年版。この論文は GoF の Iterator パターンを投射 (mapping) と累積 (accumulating) に分解することで applicative スタイルに関する議論を展開している。

論文の前半は関数型の反復と applicative スタイルの報告となっている。applicative functor に関しては、以下の 3種類あるとしている: 1. Monadic applicative functors 2. Naperian applicative functors 3. Monoidal applicative functors

全てのモナドが applicative であることは何回か話した。Naperian applicative functor は固定された形のデータ構造を zip するものだ。また、applicative functor は最初は idiom と名付けられたらしいので、この論文で idiomatic という言葉が出てきたら applicative という意味だ。

Monoidal applicatives

Scalaz は Monoid[m].applicative を実装して、どんな Monoid でも applicative に変換できる。

scala> Monoid[Int].applicative.ap2(1, 1)(0)
res99: Int = 2

scala> Monoid[List[Int]].applicative.ap2(List(1), List(1))(Nil)
res100: List[Int] = List(1, 1)

Applicative functor の組み合わせ

EIP:

Like monads, applicative functors are closed under products; so two independent idiomatic effects can generally be fused into one, their product.

Scalaz では、Applicative 型クラスに product が実装されている:

trait Applicative[F[_]] extends Apply[F] with Pointed[F] { self =>
  ...
  /**The product of Applicatives `F` and `G`, `[x](F[x], G[x]])`, is an Applicative */
  def product[G[_]](implicit G0: Applicative[G]): Applicative[({type λ[α] = (F[α], G[α])})#λ] = new ProductApplicative[F, G] {
    implicit def F = self
    implicit def G = G0
  }
  ...
}

これを使って List と Option の積を作ってみる。

scala> Applicative[List].product[Option]
res0: scalaz.Applicative[[α](List[α], Option[α])] = scalaz.Applicative$$anon$2@211b3c6a

scala> Applicative[List].product[Option].point(1)
res1: (List[Int], Option[Int]) = (List(1),Some(1))

積は Tuple2 として実装されているみたいだ。Applicative スタイルを使って append してみよう:

scala> ((List(1), 1.some) |@| (List(1), 1.some)) {_ |+| _}
res2: (List[Int], Option[Int]) = (List(1, 1),Some(2))

scala> ((List(1), 1.success[String]) |@| (List(1), "boom".failure[Int])) {_ |+| _}
res6: (List[Int], scalaz.Validation[String,Int]) = (List(1, 1),Failure(boom))

EIP:

Unlike monads in general, applicative functors are also closed under composition; so two sequentially-dependent idiomatic effects can generally be fused into one, their composition.

これは Applicative では compose と呼ばれている:

trait Applicative[F[_]] extends Apply[F] with Pointed[F] { self =>
...
  /**The composition of Applicatives `F` and `G`, `[x]F[G[x]]`, is an Applicative */
  def compose[G[_]](implicit G0: Applicative[G]): Applicative[({type λ[α] = F[G[α]]})#λ] = new CompositionApplicative[F, G] {
    implicit def F = self
    implicit def G = G0
  }
...
}

List と Option を合成してみる。

scala> Applicative[List].compose[Option]
res7: scalaz.Applicative[[α]List[Option[α]]] = scalaz.Applicative$$anon$1@461800f1

scala> Applicative[List].compose[Option].point(1)
res8: List[Option[Int]] = List(Some(1))

EIP:

The two operators ⊗ and ⊙ allow us to combine idiomatic computations in two different ways; we call them parallel and sequential composition, respectively.

Applicative を合成しても applicative が得られるのは便利だ。この特性を利用してこの論文ではモジュール性の話をしているんだと思う。

Idiomatic traversal

EIP:

Traversal involves iterating over the elements of a data structure, in the style of a map, but interpreting certain function applications idiomatically.

これに対応する Scalaz 7 での型クラスは Traverse と呼ばれている:

trait Traverse[F[_]] extends Functor[F] with Foldable[F] { self =>
  def traverseImpl[G[_]:Applicative,A,B](fa: F[A])(f: A => G[B]): G[F[B]]
}

これは traverse 演算子を導入する:

trait TraverseOps[F[_],A] extends Ops[F[A]] {
  final def traverse[G[_], B](f: A => G[B])(implicit G: Applicative[G]): G[F[B]] =
    G.traverse(self)(f)
  ...
}

List に対して使ってみる:

scala> List(1, 2, 3) traverse { x => (x > 0) option (x + 1) }
res14: Option[List[Int]] = Some(List(2, 3, 4))

scala> List(1, 2, 0) traverse { x => (x > 0) option (x + 1) }
res15: Option[List[Int]] = None

Boolean に注入された option 演算子は (x > 0) option (x + 1) を if (x > 0) Some(x + 1) else None に展開する。

EIP:

In the case of a monadic applicative functor, traversal specialises to monadic map, and has the same uses.

確かに flatMap 的な感じがする、ただし渡された関数が List を返すことを要請する代わりに [G: Applicative] であるときの G[B] を要請する。

EIP:

For a monoidal applicative functor, traversal accumulates values. The function reduce performs that accumulation, given an argument that assigns a value to each element.

scala> Monoid[Int].applicative.traverse(List(1, 2, 3)) {_ + 1}
res73: Int = 9

traverse 演算子を使って書きたかったんだけど、僕には分からなかった。

形と内容

EIP:

In addition to being parametrically polymorphic in the collection elements, the generic traverse operation is parametrised along two further dimensions: the datatype being traversed, and the applicative functor in which the traversal is interpreted. Specialising the latter to lists as a monoid yields a generic contents operation.

scala> def contents[F[_]: Traverse, A](f: F[A]): List[A] =
         Monoid[List[A]].applicative.traverse(f) {List(_)}
contents: [F[_], A](f: F[A])(implicit evidence$1: scalaz.Traverse[F])List[A]

scala> contents(List(1, 2, 3))
res87: List[Int] = List(1, 2, 3)

scala> contents(NonEmptyList(1, 2, 3))
res88: List[Int] = List(1, 2, 3)

scala> val tree: Tree[Char] = 'P'.node('O'.leaf, 'L'.leaf)
tree: scalaz.Tree[Char] = <tree>

scala> contents(tree)
res90: List[Char] = List(P, O, L)

これで Traverse をサポートするデータ構造ならばなんでも List へと変換できるようになった。contents は以下のようにも書ける:

scala> def contents[F[_]: Traverse, A](f: F[A]): List[A] =
         f.traverse[({type l[X]=List[A]})#l, A] {List(_)}
contents: [F[_], A](f: F[A])(implicit evidence$1: scalaz.Traverse[F])List[A]

The other half of the decomposition is obtained simply by a map, which is to say, a traversal interpreted in the identity idiom.

ここでの “identity idiom” とは Scalaz の Id モナドのことだ。

scala> def shape[F[_]: Traverse, A](f: F[A]): F[Unit] =
  f traverse {_ => ((): Id[Unit])}
shape: [F[_], A](f: F[A])(implicit evidence$1: scalaz.Traverse[F])F[Unit]

scala> shape(List(1, 2, 3))
res95: List[Unit] = List((), (), ())

scala> shape(tree).drawTree
res98: String = 
"()
|
()+- 
|
()`- 
"

EIP:

This pair of traversals nicely illustrates the two aspects of iterations that we are focussing on, namely mapping and accumulation.

decompose も実装してみよう:

scala> def decompose[F[_]: Traverse, A](f: F[A]) = (shape(f), contents(f))
decompose: [F[_], A](f: F[A])(implicit evidence$1: scalaz.Traverse[F])(F[Unit], List[A])

scala> decompose(tree)
res110: (scalaz.Tree[Unit], List[Char]) = (<tree>,List(P, O, L))

これは動作したけど、木構造を 2回ループしている。Applicative の積は applicative なことを覚えているよね?

scala> def decompose[F[_]: Traverse, A](f: F[A]) =
         Applicative[Id].product[({type l[X]=List[A]})#l].traverse(f) { x => (((): Id[Unit]), List(x)) }
decompose: [F[_], A](f: F[A])(implicit evidence$1: scalaz.Traverse[F])(scalaz.Scalaz.Id[F[Unit]], List[A])

scala> decompose(List(1, 2, 3, 4))
res135: (scalaz.Scalaz.Id[List[Unit]], List[Int]) = (List((), (), (), ()),List(1, 2, 3, 4))

scala> decompose(tree)
res136: (scalaz.Scalaz.Id[scalaz.Tree[Unit]], List[Char]) = (<tree>,List(P, O, L))

上の実装は monoidal applicative functor を得るのに型注釈に頼っているから Haskell のように綺麗には書けない:

decompose = traverse (shapeBody ⊗ contentsBody)

Sequence

Traverse は sequence という便利なメソッドも導入する。これは Haskell の sequence 関数に由来する命名だから、Hoogle してみる:

`haskell sequence :: Monad m => [m a] -> m [a]` Evaluate each action in the sequence from left to right, and collect the results.

これが sequence メソッドだ:

  /** Traverse with the identity function */
  final def sequence[G[_], B](implicit ev: A === G[B], G: Applicative[G]): G[F[B]] = {
    val fgb: F[G[B]] = ev.subst[F](self)
    F.sequence(fgb)
  }

Monad の代わりに要請が Applicative に緩められている。使ってみよう:

scala> List(1.some, 2.some).sequence
res156: Option[List[Int]] = Some(List(1, 2))

scala> List(1.some, 2.some, none).sequence
res157: Option[List[Int]] = None

これは使えそうだ。さらに Traverse のメソッドなため、他のデータ構造でも動く:

scala> val validationTree: Tree[Validation[String, Int]] = 1.success[String].node(
         2.success[String].leaf, 3.success[String].leaf)
validationTree: scalaz.Tree[scalaz.Validation[String,Int]] = <tree>

scala> validationTree.sequence[({type l[X]=Validation[String, X]})#l, Int]
res162: scalaz.Validation[String,scalaz.Unapply[scalaz.Traverse,scalaz.Tree[scalaz.Validation[String,Int]]]{type M[X] = scalaz.Tree[X]; type A = scalaz.Validation[String,Int]}#M[Int]] = Success(<tree>)

scala> val failedTree: Tree[Validation[String, Int]] = 1.success[String].node(
         2.success[String].leaf, "boom".failure[Int].leaf)
failedTree: scalaz.Tree[scalaz.Validation[String,Int]] = <tree>

scala> failedTree.sequence[({type l[X]=Validation[String, X]})#l, Int]
res163: scalaz.Validation[String,scalaz.Unapply[scalaz.Traverse,scalaz.Tree[scalaz.Validation[String,Int]]]{type M[X] = scalaz.Tree[X]; type A = scalaz.Validation[String,Int]}#M[Int]] = Failure(boom)

収集と拡散

EIP:

We have found it convenient to consider special cases of effectful traversals, in which the mapping aspect is independent of the accumulation, and vice versa. The ﬁrst of these traversals accumulates elements effectfully, with an operation of type a → m (), but modiﬁes those elements purely and independently of this accumulation, with a function of type a → b.

これは for ループの外側で可変な変数に累積を行なうことを真似している。Traverse は traverse を Stateモナドに特殊化した traverseS も導入する。これを使うと collect は以下のように書ける:

scala> def collect[F[_]: Traverse, A, S, B](t: F[A])(f: A => B)(g: S => S) =
         t.traverseS[S, B] { a => State { (s: S) => (g(s), f(a)) } }
collect: [F[_], A, S, B](t: F[A])(f: A => B)(g: S => S)(implicit evidence$1: scalaz.Traverse[F])scalaz.State[S,scalaz.Unapply[scalaz.Traverse,F[A]]{type M[X] = F[X]; type A = A}#M[B]]

scala> val loop = collect(List(1, 2, 3, 4)) {(_: Int) * 2} {(_: Int) + 1}
loop: scalaz.State[Int,scalaz.Unapply[scalaz.Traverse,List[Int]]{type M[X] = List[X]; type A = Int}#M[Int]] = scalaz.package$State$$anon$1@3926008a

scala> loop(0)
res165: (Int, scalaz.Unapply[scalaz.Traverse,List[Int]]{type M[X] = List[X]; type A = Int}#M[Int]) = (4,List(2, 4, 6, 8))

EIP:

The second kind of traversal modiﬁes elements purely but dependent on the state, with a binary function of type a → b → c, evolving this state independently of the elements, via a computation of type m b.

これはやっていることは traverseS と変わらない。label の実装はこうなる:

scala> def label[F[_]: Traverse, A](f: F[A]): F[Int] =
         (f.traverseS {_ => for {
           n <- get[Int]
           x <- put(n + 1)
         } yield n}) eval 0
label: [F[_], A](f: F[A])(implicit evidence$1: scalaz.Traverse[F])F[Int]

これはデータ構造の内容を無視して、0 から始まる数字で置換している。かなり副作用的 (effecty) だ。List と Tree で試してみる:

scala> label(List(10, 2, 8))
res176: List[Int] = List(0, 1, 2)

scala> label(tree).drawTree
res177: String = 
"0
|
1+- 
|
2`- 
"

リンク

EIP は Scala の関数型をやってる人の間では人気の論文みたいだ。

Eric Torreborre (@etorreborre) さんの The Essence of the Iterator Pattern が一番この論文を詳しく研究している。これは Iterator パターンの本質として僕が訳させてもらった。基礎からみていっているので、じっくり読む価値がある。

Debasish Ghosh (@debasishg) さんの Iteration in Scala - effectful yet functional は短めだけど、Scalaz に焦点を絞って良い所を持っていっている。

Marc-Daniel Ortega (@patterngazer) さんの Where we traverse, accumulate and collect in Scala も Scalaz を使って sequence や collect をみている。

続きはまた後で。

13日目 (import ガイド)

e.e d3si9n

昨日は、Jeremy Gibbons さんによる論文を 2本飛ばし読みしておりがみプログラミングと applicative な走査をみた。今日は何かを読む代わりに、Scalaz の使い方に焦点を当ててみる。

implicit のまとめ

Scalaz は implicit を使い倒している。ライブラリを使う側としても、拡張する側としても何がどこから来てるかという一般的な勘を作っていくのは大切だ。Scala の import と implicit を手早く復習しよう!

Scala では import は 2つの目的で使われる: 1. 値や型の名前をスコープに取り込むため。 2. implicit をスコープに取り込むため。

implicit には僕が考えられる限り 4つの使い方がある: 1. 型クラスインスタンスを提供するため。 2. メソッドや演算子を注入するため。(静的モンキーパッチ) 3. 型制約を宣言するため。 4. 型の情報をコンパイラから取得するため。

implicit は以下の優先順位で選択される: 1. プレフィックス無しでアクセスできる暗黙の値や変換子。ローカル宣言、import、外のスコープ、継承、および現在のパッケージオブジェクトから取り込まれる。同名の暗黙の値があった場合は内側のスコープのものが外側のものを shadow する。 2. 暗黙のスコープ。型、その部分、および親型のコンパニオンオブジェクトおよびパッケージオブジェクト内で宣言された暗黙の値や変換子。

import scalaz._

まずは import scalaz._ で何が import されるのかみてみよう。

まずは、名前だ。Equal[A] や Functor[F[_]] のような型クラスは trait として実装されていて、scalaz パッケージ内で定義されている。だから、scalaz.Equal[A] と書くかわりに Equal[A] と書ける。

次も、名前だけど、これは型エイリアス。scalaz のパッケージオブジェクトは @@[T, Tag] や Reader[E, A] (ReaderT モナド変換子を特殊化したものという扱い) のような主な型エイリアスを宣言する。これも scalaz.Reader[E, A] というふうにアクセスすることができる。

最後に、Id[A] の Traverse[F[_]] や Monad[F[_]] その他への型クラスインスタンスとして idInstance が定義されているけど、気にしなくてもいい。パッケージオブジェクトに入っているというだけで暗黙のスコープに入るので、これは import しても結果は変わらない。確かめてみよう:

scala> scalaz.Monad[scalaz.Id.Id]
res1: scalaz.Monad[scalaz.Id.Id] = scalaz.IdInstances$$anon$1@fc98c94

import は必要なしということで、うまくいった。つまり、import scalaz._ の効果はあくまで便宜のためであって、省略可能だ。

import Scalaz._

だとすると、import Scalaz._ は一体何をやっているんだろう? 以下が Scalaz object の定義だ:

package scalaz

object Scalaz
  extends StateFunctions        // Functions related to the state monad
  with syntax.ToTypeClassOps    // syntax associated with type classes
  with syntax.ToDataOps         // syntax associated with Scalaz data structures
  with std.AllInstances         // Type class instances for the standard library types
  with std.AllFunctions         // Functions related to standard library types
  with syntax.std.ToAllStdOps   // syntax associated with standard library types
  with IdInstances              // Identity type and instances

これは import をまとめるのに便利な方法だ。Scalaz object そのものは何も定義せずに、trait をミックスインしている。以下にそれぞれの trait を詳しくみていくけど、飲茶スタイルでそれぞれ別々に import することもできる。フルコースに戻ろう。

StateFunctions

import は名前と implicit を取り込む。まずは、名前だ。StateFunctions はいくつかの関数を定義する:

package scalaz

trait StateFunctions {
  def constantState[S, A](a: A, s: => S): State[S, A] = ...
  def state[S, A](a: A): State[S, A] = ...
  def init[S]: State[S, S] = ...
  def get[S]: State[S, S] = ...
  def gets[S, T](f: S => T): State[S, T] = ...
  def put[S](s: S): State[S, Unit] = ...
  def modify[S](f: S => S): State[S, Unit] = ...
  def delta[A](a: A)(implicit A: Group[A]): State[A, A] = ...
}

これらの関数を取り込むことで、get や put がグローバル関数であるかのように扱うことができる。何で? これが 7日目に見た DSL を可能にしている:

for {
  xs <- get[List[Int]]
  _ <- put(xs.tail)
} yield xs.head

std.AllFunctions

次も名前だ。std.AllFunctions もそれ自体は trait のミックスインだ:

package scalaz
package std

trait AllFunctions
  extends ListFunctions
  with OptionFunctions
  with StreamFunctions
  with math.OrderingFunctions
  with StringFunctions

object AllFunctions extends AllFunctions

上のそれぞれの trait はグローバル関数として振る舞う様々な関数をスコープに取り込む。例えば、ListFunctions はある特定の要素を 1つおきに挟み込む intersperse 関数を定義する:

scala> intersperse(List(1, 2, 3), 7)
res3: List[Int] = List(1, 7, 2, 7, 3)

微妙だ。個人的には注入されたメソッドを使うので、これらの関数は僕は使っていない。

IdInstances

IdInstances という名前だけど、これは Id[A] の型エイリアスも以下のように宣言する:

  type Id[+X] = X

名前はこれでおしまい。import は implicit も取り込むけど、implicit には 4つの使い方があると言った。特に最初の 2つ、型クラスインスタンスとメソッドや演算子の注入が大切だ。

std.AllInstances

これまでの所、僕は意図的に型クラスインスタンスという概念とメソッド注入 (別名 enrich my library) という概念をあたかも同じ事のように扱ってきた。だけど、List が Monad であることと、Monad が >>= 演算子を導入することは 2つの異なる事柄だ。

Scalaz 7 の設計方針で最も興味深いことの 1つとしてこれらの概念が徹底して “instance” (インスタンス) と “syntax” (構文) として区別されていることが挙げられる。たとえどれだけ一部のユーザにとって論理的に筋が通ったとしても、ライブラリがシンボルを使った演算子を導入すると議論の火種となる。 sbt、dispatch、specs などのライブラリやツールはそれぞれ独自の DSL を導入し、それらの効用に関して何度も議論が繰り広げられた。事を難しくするのが、複数の DSL を同時に使うと注入されたメソッドが衝突する可能性だ。

std.AllInstances は標準 (std) データ構造に対する型クラスのインスタンスのミックスインだ:

package scalaz.std

trait AllInstances
  extends AnyValInstances with FunctionInstances with ListInstances with MapInstances
  with OptionInstances with SetInstances with StringInstances with StreamInstances with TupleInstances
  with EitherInstances with PartialFunctionInstances with TypeConstraintInstances
  with scalaz.std.math.BigDecimalInstances with scalaz.std.math.BigInts
  with scalaz.std.math.OrderingInstances
  with scalaz.std.util.parsing.combinator.Parsers
  with scalaz.std.java.util.MapInstances
  with scalaz.std.java.math.BigIntegerInstances
  with scalaz.std.java.util.concurrent.CallableInstances
  with NodeSeqInstances
  // Intentionally omitted: IterableInstances

object AllInstances extends AllInstances

syntax.ToTypeClassOps

次は注入されるメソッドと演算子。これらは全て scalaz.syntax パッケージ下に入る。syntax.ToTypeClassOps は型クラスに対して注入されるメソッドを全て導入する:

package scalaz
package syntax

trait ToTypeClassOps
  extends ToSemigroupOps with ToMonoidOps with ToGroupOps with ToEqualOps with ToLengthOps with ToShowOps
  with ToOrderOps with ToEnumOps with ToMetricSpaceOps with ToPlusEmptyOps with ToEachOps with ToIndexOps
  with ToFunctorOps with ToPointedOps with ToContravariantOps with ToCopointedOps with ToApplyOps
  with ToApplicativeOps with ToBindOps with ToMonadOps with ToCojoinOps with ToComonadOps
  with ToBifoldableOps with ToCozipOps
  with ToPlusOps with ToApplicativePlusOps with ToMonadPlusOps with ToTraverseOps with ToBifunctorOps
  with ToBitraverseOps with ToArrIdOps with ToComposeOps with ToCategoryOps
  with ToArrowOps with ToFoldableOps with ToChoiceOps with ToSplitOps with ToZipOps with ToUnzipOps with ToMonadWriterOps with ToListenableMonadWriterOps

例えば、[syntax.ToBindOps] は [F: Bind] である F[A] を BindOps[F, A] に暗黙に変換して、それは >>= 演算子を実装する。

syntax.ToDataOps

syntax.ToDataOps は Scalz で定義されるデータ構造のために注入される演算子を導入する:

trait ToDataOps extends ToIdOps with ToTreeOps with ToWriterOps with ToValidationOps with ToReducerOps with ToKleisliOps

IdOps メソッドは全ての型に注入され、便宜のためにある:

package scalaz.syntax

trait IdOps[A] extends Ops[A] {
  final def ??(d: => A)(implicit ev: Null <:< A): A = ...
  final def |>[B](f: A => B): B = ...
  final def squared: (A, A) = ...
  def left[B]: (A \/ B) = ...
  def right[B]: (B \/ A) = ...
  final def wrapNel: NonEmptyList[A] = ...
  def matchOrZero[B: Monoid](pf: PartialFunction[A, B]): B = ...
  final def doWhile(f: A => A, p: A => Boolean): A = ...
  final def whileDo(f: A => A, p: A => Boolean): A = ...
  def visit[F[_] : Pointed](p: PartialFunction[A, F[A]]): F[A] = ...
}

trait ToIdOps {
  implicit def ToIdOps[A](a: A): IdOps[A] = new IdOps[A] {
    def self: A = a
  }
}

興味深い事に、ToTreeOps も全てのデータ型を TreeOps[A] に変換して 2つのメソッドを注入する:

package scalaz
package syntax

trait TreeOps[A] extends Ops[A] {
  def node(subForest: Tree[A]*): Tree[A] = ...
  def leaf: Tree[A] = ...
}

trait ToTreeOps {
  implicit def ToTreeOps[A](a: A) = new TreeOps[A]{ def self = a }
}

つまり、これらのメソッドは Tree を作るためにある。

scala> 1.node(2.leaf)
res7: scalaz.Tree[Int] = <tree>

WriterOps[A]

、ValidationOps[A]、ReducerOps[A]、そして KleisliIdOps[A] も同様だ:

scala> 1.set("log1")
res8: scalaz.Writer[String,Int] = scalaz.WriterTFunctions$$anon$26@2375d245

scala> "log2".tell
res9: scalaz.Writer[String,Unit] = scalaz.WriterTFunctions$$anon$26@699289fb

scala> 1.success[String]
res11: scalaz.Validation[String,Int] = Success(1)

scala> "boom".failureNel[Int]
res12: scalaz.ValidationNEL[String,Int] = Failure(NonEmptyList(boom))

つまり、syntax.ToDataOps にミックスインされた trait の多くは全ての型にメソッドを導入して Scalaz のデータ構造を作る。

syntax.std.ToAllStdOps

最後に、syntax.std.ToAllStdOps があって、これは Scala の標準型にメソッドや演算子を導入する。

package scalaz
package syntax
package std

trait ToAllStdOps
  extends ToBooleanOps with ToOptionOps with ToOptionIdOps with ToListOps with ToStreamOps
  with ToFunction2Ops with ToFunction1Ops with ToStringOps with ToTupleOps with ToMapOps with ToEitherOps

これは色々面白い事をやっている。BooleanOps には様々な事への略記法が導入されている:

scala> false /\ true
res14: Boolean = false

scala> false \/ true
res15: Boolean = true

scala> true option "foo"
res16: Option[String] = Some(foo)

scala> (1 > 10)? "foo" | "bar"
res17: String = bar

scala> (1 > 10)?? {List("foo")}
res18: List[String] = List()

option 演算子はとても便利だ。3項演算子は if-else よりも短い記法に見える。

OptionOps も似たようなものを導入する:

scala> 1.some? "foo" | "bar"
res28: String = foo

scala> 1.some | 2
res30: Int = 1

一方 ListOps はより伝統的な Monad 関連のものが多い:

scala> List(1, 2) filterM {_ => List(true, false)}
res37: List[List[Int]] = List(List(1, 2), List(1), List(2), List())

アラカルト形式

僕は、飲茶スタイルという名前の方がいいと思うけど、カートで点心が運ばれてきて好きなものを選んで取る飲茶でピンと来なければ、カウンターに座って好きなものを頼む焼き鳥屋だと考えてもいい。

もし何らかの理由で Scalaz._ を全て import したくなければ、好きなものを選ぶことができる。

型クラスインスタンスと関数

型クラスはデータ構造ごとに分かれている。以下が Option のための全ての型クラスインスタンスを導入する方法だ:

// fresh REPL
scala> import scalaz.std.option._
import scalaz.std.option._

scala> scalaz.Monad[Option].point(0)
res0: Option[Int] = Some(0)

これは Option に関連する「グローバル」ヘルパー関数も取り込む。Scala 標準のデータ構造は scalaz.std パッケージの下にある。

全てのインスタンスが欲しければ、以下が全て取り込む方法だ:

scala> import scalaz.std.AllInstances._
import scalaz.std.AllInstances._

scala> scalaz.Monoid[Int]
res2: scalaz.Monoid[Int] = scalaz.std.AnyValInstances$$anon$3@784e6f7c

演算子の注入を一切行なっていないので、ヘルパー関数や型クラスインスタンスに定義された関数を使う必要がある (そっちの方が好みという人もいる)。

Scalaz 型クラス syntax

型クラスの syntax は型クラスごとに分かれている。以下が Monad のためのメソッドや演算子を注入する方法だ:

scala> import scalaz.syntax.monad._
import scalaz.syntax.monad._

scala> import scalaz.std.option._
import scalaz.std.option._

scala> 0.point[Option]
res0: Option[Int] = Some(0)

見ての通り、Monad メソッドだけじゃくて、Pointed のメソッドも取り込まれた。

Tree などの Scalaz のデータ構造のための syntax も scalaz.syntax パッケージ以下にある。以下が型クラスと Scalaz データ構造のための全ての syntax を取り込む方法だ:

scala> import scalaz.syntax.all._
import scalaz.syntax.all._

scala> 1.leaf
res0: scalaz.Tree[Int] = <tree>

標準データ構造の syntax

標準データ構造の syntax はデータ構造ごとに分かれている。以下が Boolean に注入されるメソッドや演算子を取り込む方法だ:

// fresh REPL
scala> import scalaz.syntax.std.boolean._
import scalaz.syntax.std.boolean._

scala> (1 > 10)? "foo" | "bar"
res0: String = bar

標準データ構造のための全ての syntax を取り込むには:

// fresh REPL
scala> import scalaz.syntax.std.all._
import scalaz.syntax.std.all._

scala> 1.some | 2
res1: Int = 1

手早く書くつもりが、記事をまるごと使うことになった。続きはまた、後で。

14日目

bman ojel for openphoto.net

昨日は import scalaz._ と Scalaz._ が何をスコープに取り込むかをみて、アラカルト形式の import の話もした。instance や syntax がどのように構成されているのかを知ることは、実は次のステップへの準備段階で、本当にやりたいのは Scalaz をハックすることだ。

メーリングリスト

プロジェクトのハックを始める前に礼儀としてそのプロジェクトの Google Group に加入する。

git clone

$ git clone -b series/7.1.x git://github.com/scalaz/scalaz.git scalaz

上を実行すると series/7.1.x ブランチが ./scalaz ディレクトリにクローンされるはずだ。次に .git/config を以下のように編集した:

[core]
  repositoryformatversion = 0
  filemode = true
  bare = false
  logallrefupdates = true
  ignorecase = true
[remote "upstream"]
  fetch = +refs/heads/*:refs/remotes/origin/*
  url = git://github.com/scalaz/scalaz.git
[branch "series/7.1.x"]
  remote = upstream
  merge = refs/heads/series/7.1.x

これで origin のかわりに scalaz/scalaz を upstream として参照できる。変更を追従するには以下を実行する:

$ git pull --rebase
Current branch series/7.1.x is up to date.

sbt

次に sbt 0.13.5 を起動して、Scala バージョンを 2.11.1 に設定して、core プロジェクトに切り替えてコンパイルを始める:

$ sbt
scalaz> ++ 2.11.1
Setting version to 2.11.1
[info] Set current project to scalaz (in build file:/Users/eed3si9n/work/scalaz/)
scalaz> project core
[info] Set current project to scalaz-core (in build file:/Users/eed3si9n/work/scalaz/)
scalaz-core> compile

これは数分かかると思う。このビルドがスナップショットのバージョンかを確認する:

scalaz-core> version
[info] 7.0-SNAPSHOT

ローカルでコンパイルされた Scalaz を試すには、いつも通り console を使って RELP に入る:

scalaz-core> console
[info] Starting scala interpreter...
[info] 
Welcome to Scala version 2.10.1 (Java HotSpot(TM) 64-Bit Server VM, Java 1.6.0_33).
Type in expressions to have them evaluated.
Type :help for more information.

scala> [Ctrl + D to exit]

Vector を入れる

ここ 2週間使ってみて気付いた点を直してみよう。例えば、Vector のインスタンスは import Scalaz._ に入るべきだと思う。昨日 import に関して書いて記憶に新しいので楽勝だ。トピックブランチとして topic/vectorinstance を立てる:

$ git branch topic/vectorinstance
$ git co topic/vectorinstance
Switched to branch 'topic/vectorinstance'

Vector インスタンスが実際に import Scalaz._ で読み込まれていないことを sbt console から確認しよう:

$ sbt
scalaz> ++ 2.10.1
scalaz> project core
scalaz-core> console
scala> import scalaz._
import scalaz._

scala> import Scalaz._
import Scalaz._

scala> Vector(1, 2) >>= { x => Vector(x + 1)}
<console>:14: error: could not find implicit value for parameter F0: scalaz.Bind[scala.collection.immutable.Vector]
              Vector(1, 2) >>= { x => Vector(x + 1)}
                    ^

scala> Vector(1, 2) filterM { x => Vector(true, false) }
<console>:14: error: value filterM is not a member of scala.collection.immutable.Vector[Int]
              Vector(1, 2) filterM { x => Vector(true, false) }
                           ^

期待通り失敗した。

std.AllInstances を変更して VectorInstances をミックスインする:

trait AllInstances
  extends AnyValInstances with FunctionInstances with ListInstances with MapInstances
  with OptionInstances with SetInstances with StringInstances with StreamInstances
  with TupleInstances with VectorInstances
  ...

syntax.std.ToAllStdOps も変更して ToVectorOps を追加する:

trait ToAllStdOps
  extends ToBooleanOps with ToOptionOps with ToOptionIdOps with ToListOps with ToStreamOps with ToVectorOps
  ...

これだけだ。REPL で使ってみる。

scala> Vector(1, 2) >>= { x => Vector(x + 1)}
res0: scala.collection.immutable.Vector[Int] = Vector(2, 3)

scala> Vector(1, 2) filterM { x => Vector(true, false) }
res1: scala.collection.immutable.Vector[Vector[Int]] = Vector(Vector(1, 2), Vector(1), Vector(2), Vector())

動いた。こういうことに関するテストは書かれていないみたいなので、テスト無しでいく。これは “include VectorInstances and ToVectorOps to import Scalaz._” としてコミットした。次に、github で scalaz プロジェクトをフォークする。

$ git remote add fork git@github.com:yourname/scalaz.git
$ git push fork topic/vectorinstance
...
 * [new branch]      topic/vectorinstance -> topic/vectorinstance

コメントと共に pull request を投げたので、あとは向こう次第だ。次の機能の作業をするために scalaz-seven ブランチに巻き戻す必要がある。ローカルで新機能を試したいのでスナップショット用のブランチも作る。

snapshot

$ git co scalaz-seven
Switched to branch 'scalaz-seven'
$ git branch snapshot
$ git co snapshot
$ git merge topic/vectorinstance

このブランチが Scalaz で遊ぶためのサンドボックスとなる。

<*> operator

次は、Apply の <*> 演算子だけど、これは本当に M2 と Haskell の振る舞いに戻って欲しい。これは既にメーリングリストで聞いていて作者は元に戻す予定みたいなことを言っている。

$ git co scalaz-seven
Switched to branch 'scalaz-seven'
$ git branch topic/applyops
$ git co topic/applyops
Switched to branch 'topic/applyops'

これはテストファーストでやるべきだ。ApplyTest に例を加える:

  "<*>" in {
    some(9) <*> some({(_: Int) + 3}) must be_===(some(12))
  }

この build.scala で使われている specs は Scala 2.9.2 向けみたいだ。

$ sbt
scalaz> ++ 2.9.2
Setting version to 2.9.2
scalaz> project tests
scalaz-tests> test-only scalaz.ApplyTest
[error] /Users/eed3si9n/work/scalaz-seven/tests/src/test/scala/scalaz/ApplyTest.scala:38: type mismatch;
[error]  found   : org.specs2.matcher.Matcher[Option[Int]]
[error]  required: org.specs2.matcher.Matcher[Option[(Int, Int => Int)]]
[error]     some(9) <*> some({(_: Int) + 3}) must be_===(some(12))
[error]                                                 ^
[error] one error found
[error] (tests/test:compile) Compilation failed

=== が使われていてコンパイルさえしない。良し。

<*> は ApplyOps にあるので、F.ap に戻す:

  final def <*>[B](f: F[A => B]): F[B] = F.ap(self)(f)

テストを再実行してみよう:

scalaz-tests> test-only scalaz.ApplyTest
[info] ApplyTest
[info] 
[info] + mapN
[info] + apN
[info] + <*>
[info]  
[info] Total for specification ApplyTest
[info] Finished in 5 seconds, 27 ms
[info] 3 examples, 0 failure, 0 error
[info] 
[info] Passed: : Total 3, Failed 0, Errors 0, Passed 3, Skipped 0
[success] Total time: 9 s, completed Sep 19, 2012 1:57:29 AM

これは “roll back <*> as infix of ap” とコミットして、push する。

$ git push fork topic/applyops
...
 * [new branch]      topic/applyops -> topic/applyops

これも一言コメントを書いて pull request を送る。snapshot ブランチにも取り込もう:

$ git co snapshot
$ git merge topic/applyops

これで変更した点を両方とも試すことができる。

applicative 関数

これまでの変更は簡単な修正だった。ここから始まるのは applicative 関数の実験だ。

The Essence of the Iterator Pattern は、applicative functor を組み合わせるという興味深いアイディアを提唱している。実際に行われているのは applicative functor の組み合わせ (m ⊠ n) だけじゃなくて、applicative 関数の組み合わせだ:

(⊗)::(Functor m,Functor n) ⇒ (a → m b) → (a → n b) → (a → (m ⊠ n) b)
(f ⊗ g) x = Prod (f x) (g x)

Int は Monoid で、全ての Monoid は applicative functor として扱え、それは monoidal applicative と呼ばれる。問題はこれを関数にすると Int => Int と区別がつかないけど、Int => [α]Int が必要なことだ。

僕の最初のアイディアは Tags.Monoidal という名前の型タグを使って以下のように書くことだった:

scala> { (x: Int) => Tags.Monoidal(x + 1) }

これは [A:Monoid] である全ての A @@ Tags.Monoidal を applicative として認識する必要がある。ここで僕はつまずいた。

次のアイディアは Kleisli のエイリアスとして Monoidal を宣言して、以下のコンパニオンを定義することだった:

  object Monoidal {
    def apply[A: Monoid](f: A => A): Kleisli[({type λ[+α]=A})#λ, A, A] =
      Kleisli[({type λ[+α]=A})#λ, A, A](f)
  }

これで monoidal 関数を以下のように書ける:

scala> Monoidal { x: Int => x + 1 }
res4: scalaz.Kleisli[[+α]Int,Int,Int] = scalaz.KleisliFunctions$$anon$18@1a0ceb34

だけど、コンパイラは [+α]Int から自動的に Applicative を検知してくれなかった:

scala> List(1, 2, 3) traverseKTrampoline { x => Monoidal { _: Int => x + 1 } } 
<console>:14: error: no type parameters for method traverseKTrampoline: (f: Int => scalaz.Kleisli[G,S,B])(implicit evidence$2: scalaz.Applicative[G])scalaz.Kleisli[G,S,List[B]] exist so that it can be applied to arguments (Int => scalaz.Kleisli[[+α]Int,Int,Int])
 --- because ---
argument expression's type is not compatible with formal parameter type;
 found   : Int => scalaz.Kleisli[[+α]Int,Int,Int]
 required: Int => scalaz.Kleisli[?G,?S,?B]

              List(1, 2, 3) traverseKTrampoline { x => Monoidal { _: Int => x + 1 } } 
                            ^

これが悪名高い SI-2712 なのだろうか? これで思ったのは、実際の型に変えてしまえばいいということだ:

trait MonoidApplicative[F] extends Applicative[({type λ[α]=F})#λ] { self =>
  implicit def M: Monoid[F]
  def point[A](a: => A) = M.zero
  def ap[A, B](fa: => F)(f: => F) = M.append(f, fa)
  override def map[A, B](fa: F)(f: (A) => B) = fa
}

これは x + 1 を MonoidApplicative 変換しなければいけないのでうまくいかない。

次に試したのは Unapply だ:

scala> List(1, 2, 3) traverseU {_ + 1}
<console>:14: error: Unable to unapply type `Int` into a type constructor of kind `M[_]` that is classified by the type class `scalaz.Applicative`
1) Check that the type class is defined by compiling `implicitly[scalaz.Applicative[<type constructor>]]`.
2) Review the implicits in object Unapply, which only cover common type 'shapes'
(implicit not found: scalaz.Unapply[scalaz.Applicative, Int])
              List(1, 2, 3) traverseU {_ + 1}
                            ^

これはうまくいくかもしれない。Int を Unapply の中で ({type λ[α]=Int})#λ に展開するだけでいい:

trait Unapply_3 {
  /** Unpack a value of type `A0` into type `[a]A0`, given a instance of `TC` */
  implicit def unapplyA[TC[_[_]], A0](implicit TC0: TC[({type λ[α] = A0})#λ]): Unapply[TC, A0] {
    type M[X] = A0
    type A = A0
  } = new Unapply[TC, A0] {
    type M[X] = A0
    type A = A0
    def TC = TC0
    def apply(ma: M[A0]) = ma
  }
}

試してみる:

scala> List(1, 2, 3) traverseU {_ + 1}
res0: Int = 9

実際にうまくいった! 組み合わせはどうだろう?

scala> val f = { (x: Int) => x + 1 }
f: Int => Int = <function1>

scala> val g = { (x: Int) => List(x, 5) }
g: Int => List[Int] = <function1>

scala> val h = f &&& g
h: Int => (Int, List[Int]) = <function1>

scala> List(1, 2, 3) traverseU f
res0: Int = 9

scala> List(1, 2, 3) traverseU g
res1: List[List[Int]] = List(List(1, 2, 3), List(1, 2, 5), List(1, 5, 3), List(1, 5, 5), List(5, 2, 3), List(5, 2, 5), List(5, 5, 3), List(5, 5, 5))

scala> List(1, 2, 3) traverseU h
res2: (Int, List[List[Int]]) = (9,List(List(1, 5), List(2, 5), List(3, 5)))

これは res1 か res2 が間違っているんじゃないかと思う。res1 は僕が Haskell で確認した結果と同じものを返している。Tuple2 も applicative だから、そこで予想外のことをやっているのかもしれない。僕の変更無しでも同じ振る舞いを確認できたので、テストを書く:

    "traverse int function as monoidal applicative" in {
      val s: Int = List(1, 2, 3) traverseU {_ + 1}
      s must be_===(9)
    }

走らせてみる:

scalaz-tests> test-only scalaz.TraverseTest
[info] list should
[info] + apply effects in order
[info] + traverse through option effect
[info] + traverse int function as monoidal applicative
[info] + not blow the stack
[info] + state traverse agrees with regular traverse
[info] + state traverse does not blow stack
...
[success] Total time: 183 s, completed Sep 19, 2012 8:09:03 AM

scalaz-seven から topic/unapplya ブランチを立てる:

$ git co scalaz-seven
M core/src/main/scala/scalaz/Unapply.scala
M tests/src/test/scala/scalaz/TraverseTest.scala
Switched to branch 'scalaz-seven'
$ git branch topic/unapplya
$ git co topic/unapplya
M core/src/main/scala/scalaz/Unapply.scala
M tests/src/test/scala/scalaz/TraverseTest.scala
Switched to branch 'topic/unapplya'

全テストが通過すれば、“adds implicit def unapplyA, which unpacks A into [a]A” としてコミットする。

$ git push fork topic/unapplya
...
 * [new branch]      topic/unapplya -> topic/unapplya

これも pull request にして送る。これは、なかなか楽しかった。

続きはまた後で。

15日目

14日目に Scalaz をハックし始めた。まず、Vector の型クラスインスタンスが import Scalaz._ に含まれるようにした。次に、<*> を ap の中置記法に振り戻した。最後に、コンパイラが Applicative[({type λ[α]=Int})#λ] を見つけられるように A を [α]A に展開する暗黙の変換子を追加した。

3つの pull request とも上流に取り込んでもらえた! 以下の方法で早速同期する:

$ git co scalaz-seven
$ git pull --rebase

一度落ち着いて僕らがいじった型クラスをみてみよう。

Rodolfo Cartas for openphoto.net

Arrow

射とは、圏論の用語で関数っぽい振る舞いをするものの抽象概念だ。Scalaz だと Function1[A, B]、PartialFunction[A, B]、Kleisli[F[_], A, B]、そして CoKleisli[F[_], A, B] がこれにあたる。他の型クラスがコンテナを抽象化するのと同様に Arrow はこれらを抽象化する。

以下が Arrow の型クラスコントラクトだ:

trait Arrow[=>:[_, _]] extends Category[=>:] { self =>
  def id[A]: A =>: A
  def arr[A, B](f: A => B): A =>: B
  def first[A, B, C](f: (A =>: B)): ((A, C) =>: (B, C))
}

Arrow[=>:[_, _]] は Category[=>:] を継承するみたいだ。

Category と Compose

以下が Category[=>:[_, _]] だ:

trait Category[=>:[_, _]] extends ArrId[=>:] with Compose[=>:] { self =>
  // no contract function
}

これは Compose[=>:] を継承する:

trait Compose[=>:[_, _]]  { self =>
  def compose[A, B, C](f: B =>: C, g: A =>: B): (A =>: C)
}

compose 関数は 2つの射を合成する。Compose は以下の演算子を導入する:

trait ComposeOps[F[_, _],A, B] extends Ops[F[A, B]] {
  final def <<<[C](x: F[C, A]): F[C, B] = F.compose(self, x)
  final def >>>[C](x: F[B, C]): F[A, C] = F.compose(x, self)
}

>>> と <<< の意味は射に依存するけど、関数の場合は andThen と compose と同じだ:

scala> val f = (_:Int) + 1
f: Int => Int = <function1>

scala> val g = (_:Int) * 100
g: Int => Int = <function1>

scala> (f >>> g)(2)
res0: Int = 300

scala> (f <<< g)(2)
res1: Int = 201

Arrow、再び

Arrow[=>:[_, _]] の型宣言は少し変わってみえるけど、これは Arrow[M[_, _]] と言っているのと変わらない。2つのパラメータを取る型コンストラクタで便利なのは =>:[A, B] を A =>: B のように中置記法で書けることだ。

arr 関数は普通の関数から射を作り、id は恒等射を返し、first は既存の射の出入力をペアに拡張した新しい射を返す。

上記の関数を使って、Arrow は以下の演算子を導入する:

trait ArrowOps[F[_, _],A, B] extends Ops[F[A, B]] {
  final def ***[C, D](k: F[C, D]): F[(A, C), (B, D)] = F.splitA(self, k)
  final def &&&[C](k: F[A, C]): F[A, (B, C)] = F.combine(self, k)
  ...
}

Haskell の Arrow tutorial を読んでみる:

(***) combines two arrows into a new arrow by running the two arrows on a pair of values (one arrow on the first item of the pair and one arrow on the second item of the pair).
(***) は 2つの射を値のペアに対して (1つの射はペアの最初の項で、もう 1つの射はペアの 2つめの項で) 実行することで 1つの新しいに射へと組み合わせる。

具体例で説明すると:

scala> (f *** g)(1, 2)
res3: (Int, Int) = (2,200)

(&&&) は 2つの射を両方とも同じ値に対して実行することで 1つの新しい射へと組み合わせる:

以下が &&& の例:

scala> (f &&& g)(2)
res4: (Int, Int) = (3,200)

関数やペアにらんらかのコンテキストを与えたい場合は射が便利かもしれない。

Unapply

Scala コンパイラで苦労させられているのは、例えば F[M[_, _]] と F[M[_]] や M[_] と F[M[_]] など異なるカインド付けされた型の間での型推論が無いことだ。

具体的には、Applicative[M[_]] のインスタンスは (* -> *) -> * (ただ 1つの型を受け取る型コンストラクタを受け取る型コンストラクタ) だ。Int => Int を Int => A として扱うことで applicative として扱えることが知られている:

scala> Applicative[Function1[Int, Int]]
<console>:14: error: Int => Int takes no type parameters, expected: one
              Applicative[Function1[Int, Int]]
                          ^

scala> Applicative[({type l[A]=Function1[Int, A]})#l]
res14: scalaz.Applicative[[A]Int => A] = scalaz.std.FunctionInstances$$anon$2@56ae78ac

これは Validation のような M[_,_] で面倒になる。Scalaz が手伝ってくれる 1つの方法として Unapply というメタインスタンスがある。

trait Unapply[TC[_[_]], MA] {
  /** The type constructor */
  type M[_]
  /** The type that `M` was applied to */
  type A
  /** The instance of the type class */
  def TC: TC[M]
  /** Evidence that MA =:= M[A] */
  def apply(ma: MA): M[A]
}

traverse などの Scalaz のメソッドが Applicative[M[_]] を要請するとき、代わりに Unapply[Applicative, X] を要請できる。コンパイル時に Scalac は Function1[Int, Int] を M[A] に強制できないかをパラメータを固定したり、追加したり、もちろん既存の型クラスインスタンスを利用したりして暗黙の変換子を全て試す。

scala> implicitly[Unapply[Applicative, Function1[Int, Int]]]
res15: scalaz.Unapply[scalaz.Applicative,Int => Int] = scalaz.Unapply_0$$anon$9@2e86566f

僕が昨日追加したのは型 A に偽の型コンストラクタをつけて M[A] に昇進させる方法だ。これによって Int を Applicative として扱いやすくなる。だけど、TC0: TC[({type λ[α] = A0})#λ] を暗黙に要請するから、どの型でも Applicative に昇進できるというわけではない。

scala> implicitly[Unapply[Applicative, Int]]
res0: scalaz.Unapply[scalaz.Applicative,Int] = scalaz.Unapply_3$$anon$1@5179dc20

scala> implicitly[Unapply[Applicative, Any]]
<console>:14: error: Unable to unapply type `Any` into a type constructor of kind `M[_]` that is classified by the type class `scalaz.Applicative`
1) Check that the type class is defined by compiling `implicitly[scalaz.Applicative[<type constructor>]]`.
2) Review the implicits in object Unapply, which only cover common type 'shapes'
(implicit not found: scalaz.Unapply[scalaz.Applicative, Any])
              implicitly[Unapply[Applicative, Any]]
                        ^

動いた。これらの結果として以下のようなコードが少しきれいに書けるようになる:

scala> val failedTree: Tree[Validation[String, Int]] = 1.success[String].node(
         2.success[String].leaf, "boom".failure[Int].leaf)
failedTree: scalaz.Tree[scalaz.Validation[String,Int]] = <tree>

scala> failedTree.sequence[({type l[X]=Validation[String, X]})#l, Int]
res2: scalaz.Validation[java.lang.String,scalaz.Tree[Int]] = Failure(boom)

以下が sequenceU を用いたもの:

scala> failedTree.sequenceU
res3: scalaz.Validation[String,scalaz.Tree[Int]] = Failure(boom)

ブーム。

並列合成

Unapply に加えた変更で monoidal applicative functor は動くようになったけど、組み合わせはまだできない:

scala> val f = { (x: Int) => x + 1 }
f: Int => Int = <function1>

scala> val g = { (x: Int) => List(x, 5) }
g: Int => List[Int] = <function1>

scala> val h = f &&& g
h: Int => (Int, List[Int]) = <function1>

scala> List(1, 2, 3) traverseU f
res0: Int = 9

scala> List(1, 2, 3) traverseU g
res1: List[List[Int]] = List(List(1, 2, 3), List(1, 2, 5), List(1, 5, 3), List(1, 5, 5), List(5, 2, 3), List(5, 2, 5), List(5, 5, 3), List(5, 5, 5))

scala> List(1, 2, 3) traverseU h
res2: (Int, List[List[Int]]) = (9,List(List(1, 5), List(2, 5), List(3, 5)))

f と g は動く。問題は traverseU のペアの解釈だ。f と g を手で組み合わせるとこうなる:

scala> val h = { (x: Int) => (f(x), g(x)) }
h: Int => (Int, List[Int]) = <function1>

これが Tuple2Functor だ:

private[scalaz] trait Tuple2Functor[A1] extends Functor[({type f[x] = (A1, x)})#f] {
  override def map[A, B](fa: (A1, A))(f: A => B) =
    (fa._1, f(fa._2))
}

Scalaz には確かに applicative functor の積という概念はあって Apply 型クラスに product メソッドがあるんだけど、ペアを使ってエンコードしているせいで implicits が提供されていない。現時点では、Scalaz に EIP に記述されているように applicative 関数 (A => M[B]) の積を実装する方法があるかは不明だ:

data (m ⊠ n) a = Prod {pfst ::m a,psnd :: n a}
(⊗)::(Functor m,Functor n) ⇒ (a → m b) → (a → n b) → (a → (m ⊠ n) b)
(f ⊗ g) x = Prod (f x) (g x)

これは合成に関しても言えることだ。scalaz-seven ブランチからブランチする:

$ git co scalaz-seven
Already on 'scalaz-seven'
$ git branch topic/appcompose
$ git co topic/appcompose
Switched to branch 'topic/appcompose'

とりあえず実際の型に保存してみて、きれいに直す心配は後にしよう。

package scalaz

import Id._

trait XProduct[A, B] {
  def _1: A
  def _2: B
  override def toString: String = "XProduct(" + _1.toString + ", " + _2.toString + ")"
}

trait XProductInstances {
  implicit def productSemigroup[A1, A2](implicit A1: Semigroup[A1], A2: Semigroup[A2]): Semigroup[XProduct[A1, A2]] = new XProductSemigroup[A1, A2] {
    implicit def A1 = A1
    implicit def A2 = A2
  }  
  implicit def productFunctor[F[_], G[_]](implicit F0: Functor[F], G0: Functor[G]): Functor[({type λ[α] = XProduct[F[α], G[α]]})#λ] = new XProductFunctor[F, G] {
    def F = F0
    def G = G0
  }
  implicit def productPointed[F[_], G[_]](implicit F0: Pointed[F], G0: Pointed[G]): Pointed[({type λ[α] = XProduct[F[α], G[α]]})#λ] = new XProductPointed[F, G] {
    def F = F0
    def G = G0
  }
  implicit def productApply[F[_], G[_]](implicit F0: Apply[F], G0: Apply[G]): Apply[({type λ[α] = XProduct[F[α], G[α]]})#λ] = new XProductApply[F, G] {
    def F = F0
    def G = G0
  }
  implicit def productApplicativeFG[F[_], G[_]](implicit F0: Applicative[F], G0: Applicative[G]): Applicative[({type λ[α] = XProduct[F[α], G[α]]})#λ] = new XProductApplicative[F, G] {
    def F = F0
    def G = G0
  }
  implicit def productApplicativeFB[F[_], B](implicit F0: Applicative[F], B0: Applicative[({type λ[α] = B})#λ]): Applicative[({type λ[α] = XProduct[F[α], B]})#λ] = new XProductApplicative[F, ({type λ[α] = B})#λ] {
    def F = F0
    def G = B0
  }
  implicit def productApplicativeAG[A, G[_]](implicit A0: Applicative[({type λ[α] = A})#λ], G0: Applicative[G]): Applicative[({type λ[α] = XProduct[A, G[α]]})#λ] = new XProductApplicative[({type λ[α] = A})#λ, G] {
    def F = A0
    def G = G0
  }
  implicit def productApplicativeAB[A, B](implicit A0: Applicative[({type λ[α] = A})#λ], B0: Applicative[({type λ[α] = B})#λ]): Applicative[({type λ[α] = XProduct[A, B]})#λ] = new XProductApplicative[({type λ[α] = A})#λ, ({type λ[α] = B})#λ] {
    def F = A0
    def G = B0
  }  
}

trait XProductFunctions {
  def product[A, B](a1: A, a2: B): XProduct[A, B] = new XProduct[A, B] {
    def _1 = a1
    def _2 = a2
  }
}

object XProduct extends XProductFunctions with XProductInstances {
  def apply[A, B](a1: A, a2: B): XProduct[A, B] = product(a1, a2)
}
private[scalaz] trait XProductSemigroup[A1, A2] extends Semigroup[XProduct[A1, A2]] {
  implicit def A1: Semigroup[A1]
  implicit def A2: Semigroup[A2]
  def append(f1: XProduct[A1, A2], f2: => XProduct[A1, A2]) = XProduct(
    A1.append(f1._1, f2._1),
    A2.append(f1._2, f2._2)
    )
}
private[scalaz] trait XProductFunctor[F[_], G[_]] extends Functor[({type λ[α] = XProduct[F[α], G[α]]})#λ] {
  implicit def F: Functor[F]
  implicit def G: Functor[G]
  override def map[A, B](fa: XProduct[F[A], G[A]])(f: (A) => B): XProduct[F[B], G[B]] =
    XProduct(F.map(fa._1)(f), G.map(fa._2)(f))
}

private[scalaz] trait XProductPointed[F[_], G[_]] extends Pointed[({type λ[α] = XProduct[F[α], G[α]]})#λ] with XProductFunctor[F, G] {
  implicit def F: Pointed[F]
  implicit def G: Pointed[G]
  def point[A](a: => A): XProduct[F[A], G[A]] = XProduct(F.point(a), G.point(a))
}

private[scalaz] trait XProductApply[F[_], G[_]] extends Apply[({type λ[α] = XProduct[F[α], G[α]]})#λ] with XProductFunctor[F, G] {
  implicit def F: Apply[F]
  implicit def G: Apply[G]
  def ap[A, B](fa: => XProduct[F[A], G[A]])(f: => XProduct[F[A => B], G[A => B]]): XProduct[F[B], G[B]] =
    XProduct(F.ap(fa._1)(f._1), G.ap(fa._2)(f._2))
}

private[scalaz] trait XProductApplicative[F[_], G[_]] extends Applicative[({type λ[α] = XProduct[F[α], G[α]]})#λ] with XProductPointed[F, G] {
  implicit def F: Applicative[F]
  implicit def G: Applicative[G]
  def ap[A, B](fa: => XProduct[F[A], G[A]])(f: => XProduct[F[(A) => B], G[(A) => B]]): XProduct[F[B], G[B]] =
    XProduct(F.ap(fa._1)(f._1), G.ap(fa._2)(f._2))
}

実装のほとんどは Tuple2 を使ってる Product.scala から奪ってきた。これが XProduct を使った最初の試みだ:

scala> XProduct(1.some, 2.some) map {_ + 1}
<console>:14: error: Unable to unapply type `scalaz.XProduct[Option[Int],Option[Int]]` into a type constructor of kind `M[_]` that is classified by the type class `scalaz.Functor`
1) Check that the type class is defined by compiling `implicitly[scalaz.Functor[<type constructor>]]`.
2) Review the implicits in object Unapply, which only cover common type 'shapes'
(implicit not found: scalaz.Unapply[scalaz.Functor, scalaz.XProduct[Option[Int],Option[Int]]])
              XProduct(1.some, 2.some) map {_ + 1}
                      ^

解読できれば、このエラーメッセージは実際役に立つものだ。これは Unapply メタインスタンスを探している。おそらくこの形のものがまだ定義されていないんだと思う。以下が新しい unapply だ:

  implicit def unapplyMFGA[TC[_[_]], F[_], G[_], M0[_, _], A0](implicit TC0: TC[({type λ[α] = M0[F[α], G[α]]})#λ]): Unapply[TC, M0[F[A0], G[A0]]] {
    type M[X] = M0[F[X], G[X]]
    type A = A0
  } = new Unapply[TC, M0[F[A0], G[A0]]] {
    type M[X] = M0[F[X], G[X]]
    type A = A0
    def TC = TC0
    def apply(ma: M0[F[A0], G[A0]]) = ma
  }

もう 1度。

scala> XProduct(1.some, 2.some) map {_ + 1}
res0: scalaz.Unapply[scalaz.Functor,scalaz.XProduct[Option[Int],Option[Int]]]{type M[X] = scalaz.XProduct[Option[X],Option[X]]; type A = Int}#M[Int] = XProduct(Some(2), Some(3))

普通の applicative としても使える:

scala> (XProduct(1, 2.some) |@| XProduct(3, none[Int])) {_ |+| (_: XProduct[Int, Option[Int]]) }
res1: scalaz.Unapply[scalaz.Apply,scalaz.XProduct[Int,Option[Int]]]{type M[X] = scalaz.XProduct[Int,Option[Int]]; type A = scalaz.XProduct[Int,Option[Int]]}#M[scalaz.XProduct[Int,Option[Int]]] = XProduct(4, Some(2))

EIP の word count の例題を書き換えてみる。

scala> val text = "the cat in the hat\n sat on the mat\n".toList
text: List[Char] = 
List(t, h, e,  , c, a, t,  , i, n,  , t, h, e,  , h, a, t, 
,  , s, a, t,  , o, n,  , t, h, e,  , m, a, t, 
)

scala> def count[A] = (a: A) => 1
count: [A]=> A => Int

scala> val charCount = count[Char]
charCount: Char => Int = <function1>

scala> text traverseU charCount
res10: Int = 35

scala> import scalaz.std.boolean.test
import scalaz.std.boolean.test

scala> val lineCount = (c: Char) => test(c === '\n')
lineCount: Char => Int = <function1>

scala> text traverseU lineCount
res11: Int = 2

scala> val wordCount = (c: Char) => for {
         x <- get[Boolean]
         val y = c =/= ' '
         _ <- put(y)
       } yield test(y /\ !x)
wordCount: Char => scalaz.StateT[scalaz.Id.Id,Int,Int] = <function1>

scala> (text traverseU wordCount) eval false count(_ > 0)
res25: Int = 9

scala> text traverseU { (c: Char) => XProduct(charCount(c), lineCount(c)) }
res26: scalaz.XProduct[Int,Int] = XProduct(35, 2)

これで applicative 関数を並列に組み合わせることができた。ペアを使ったとしたらどうなるって?

scala> text traverseU { (c: Char) => (charCount(c), lineCount(c)) }
res27: (Int, List[Int]) = (35,List(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1))

笑! だけど、Unapply の問題はより複雑な構造には対応できないことだ:

scala> text traverseU { (c: Char) => XProduct(charCount(c), wordCount(c)) }
<console>:19: error: Unable to unapply type `scalaz.XProduct[Int,scalaz.StateT[scalaz.Id.Id,Boolean,Int]]` into a type constructor of kind `M[_]` that is classified by the type class `scalaz.Applicative`
1) Check that the type class is defined by compiling `implicitly[scalaz.Applicative[<type constructor>]]`.
2) Review the implicits in object Unapply, which only cover common type 'shapes'
(implicit not found: scalaz.Unapply[scalaz.Applicative, scalaz.XProduct[Int,scalaz.StateT[scalaz.Id.Id,Boolean,Int]]])
              text traverseU { (c: Char) => XProduct(charCount(c), wordCount(c)) }
                   ^

これらが解決できれば、Arrow か Function1 に @>>> と @&&& 演算子があって EIP で書かれているような applicative の合成ができれば便利だと思う。

次回からはまた別のトピックをカバーしよう。

16日目

昨日は関数のようなものを抽象化する方法としての Arrow、それから型クラスのメタインスタンスを提供する方法としての Unapply をみた。また、applicative の実験として並行合成をサポートする XProduct も実装した。

Memo

関数が純粋だからといってその計算量が安いとは限らない。例えば、全ての 8文字の ASCII 文字列の順列に対する SHA-1 ハッシュのリストを求めるとする。タブ文字を抜くと ASCII には 95 の表示可能な文字があるので、繰り上げて 100 とする。100 ^ 8 は 10 ^ 16 だ。たとえ秒間 1000 ハッシュ処理できたとしても 10 ^ 13 秒、つまり 316888年かかる。

RAM に少し余裕があれば、計算結果をキャッシュすることで高価な計算とスペースをトレードすることができる。これはメモ化と呼ばれる。以下が Memo のコントラクトだ:

sealed trait Memo[@specialized(Int) K, @specialized(Int, Long, Double) V] {
  def apply(z: K => V): K => V
}

潜在的に高価な関数をインプットに渡して、同様に振る舞うけども結果をキャッシュする関数を返してもらう。Memo object の下に Memo.mutableHashMapMemo[K, V]、Memo.weakHashMapMemo[K, V]、や Memo.arrayMemo[V] などのいくつかの Memo のデフォルト実装がある。

一般的に、これらの最適化のテクニックは気をつけるべきだ。まず、全体の性能をプロファイルして実際に時間を節約できるのか確認するべきだし、スペースとのトレードオフも永遠に増大し続けないか解析したほうがいい。

Memoization tutorial にあるフィボナッチ数の例を実装してみよう:

scala> val slowFib: Int => Int = {
         case 0 => 0
         case 1 => 1
         case n => slowFib(n - 2) + slowFib(n - 1)
       }
slowFib: Int => Int = <function1>

scala> slowFib(30)
res0: Int = 832040

scala> slowFib(40)
res1: Int = 102334155

scala> slowFib(45)
res2: Int = 1134903170

showFib(45) は返ってくるのに少し時間がかかった。次がメモ化版:

scala> val memoizedFib: Int => Int = Memo.mutableHashMapMemo {
         case 0 => 0
         case 1 => 1
         case n => memoizedFib(n - 2) + memoizedFib(n - 1)
       }
memoizedFib: Int => Int = <function1>

scala> memoizedFib(30)
res12: Int = 832040

scala> memoizedFib(40)
res13: Int = 102334155

scala> memoizedFib(45)
res14: Int = 1134903170

結果が即座に返ってくるようになった。便利なのはメモ化した関数を作る側も使う側もあまり意識せずにできることだ。Adam Rosien さんも Scalaz “For the Rest of Us” talk (動画) でこの点を言っている。

関数型プログラミング

関数型プログラミングとは何だろう? Rúnar Óli さんはこう定義している:

関数を使ったプログラミング。

関数とは何だろう?

f: A => B 型が A の全ての値を、唯一の型が B の値に関連付け他には何もしない。

この「他には何もしない」という部分を説明するために、以下のように参照透過性という概念を導入する:

式 e は、プログラムの観測可能な結果に影響を与えることなく使われている全ての e をその値に置き換えることができるとき参照透過だ。

この概念を使うと、関数型プログラミングとは参照的に透過な式の木を組み上げていくことだと考えることができる。メモ化はこの参照透過性を利用した方法の 1つだ。

エフェクトシステム

Lazy Functional State Threads において John Launchbury さんと Simon Peyton-Jones さん曰く:

Based on earlier work on monads, we present a way of securely encapsulating stateful computations that manipulate multiple, named, mutable objects, in the context of a non-strict purely-functional language.

Scala には var があるので一見すると不必要にも思われるけど、stateful な計算をカプセル化するという考え方は役に立つことがある。並列に実行される計算など特殊な状況下では、状態が共有されないかもしくは慎重に共有されているかどうかが正誤を分ける。

ST

この論文で説明される ST に対応するものとして Scalaz には ST モナドがある。Rúnar さんの Towards an Effect System in Scala, Part 1: ST Monad も参照。以下が ST のコントラクトだ:

sealed trait ST[S, A] {
  private[effect] def apply(s: World[S]): (World[S], A)
}

State モナドに似ているけども、違いは状態が可変で上書きされていることと、その引き換えとして状態が外から観測できないことにある。

STRef

LFST:

What, then is a “state”? Part of every state is a finite mapping from reference to values. … A reference can be thought of as the name of (or address of) a variable, an updatable location in the state capable of holding a value.

STRef は ST モナドのコンテキストの内部でしか使えない可変変数だ。ST.newVar[A] によって作られ以下の演算をサポートする:

sealed trait STRef[S, A] {
  protected var value: A

  /**Reads the value pointed at by this reference. */
  def read: ST[S, A] = returnST(value)
  /**Modifies the value at this reference with the given function. */
  def mod[B](f: A => A): ST[S, STRef[S, A]] = ...
  /**Associates this reference with the given value. */
  def write(a: => A): ST[S, STRef[S, A]] = ...
  /**Synonym for write*/
  def |=(a: => A): ST[S, STRef[S, A]] = ...
  /**Swap the value at this reference with the value at another. */
  def swap(that: STRef[S, A]): ST[S, Unit] = ...
}

自家版の Scalaz 7 を使う:

$ sbt
scalaz> project effect
scalaz-effect> console
[info] Compiling 2 Scala sources to /Users/eed3si9n/work/scalaz-seven/effect/target/scala-2.9.2/classes...
[info] Starting scala interpreter...
[info]

scala> import scalaz._, Scalaz._, effect._, ST._
import scalaz._
import Scalaz._
import effect._
import ST._

scala> def e1[S] = for {
         x <- newVar[S](0)
         r <- x mod {_ + 1}
       } yield x
e1: [S]=> scalaz.effect.ST[S,scalaz.effect.STRef[S,Int]]

scala> def e2[S]: ST[S, Int] = for {
         x <- e1[S]
         r <- x.read
       } yield r 
e2: [S]=> scalaz.effect.ST[S,Int]

scala> type ForallST[A] = Forall[({type λ[S] = ST[S, A]})#λ]
defined type alias ForallST

scala> runST(new ForallST[Int] { def apply[S] = e2[S] })
res5: Int = 1

Rúnar さんのブログに Paul Chiusano さん (@pchiusano) が皆が思っていることを言っている:

僕はこれの Scala での効用について決めかねているんだけど - わざと反対の立場をとってるんだけど - もし (例えば quicksort) なんらかのアルゴリズムを実装するためにローカルで可変状態が必要なら、関数に渡されたものさえ上書き変更しなければいいだけだ。これを正しくやったとコンパイラをわざわざ説得する意義はある? 別にここでコンパイラの助けを借りなくてもいいと思う。

30分後に帰ってきて、自分の問に答えている:

もし僕が命令形の quicksort を書いているなら、インプットの列を配列にコピーしてソートの最中に上書き変更して、結果をソートされた配列にたいする不変な列のビューとして返すだろう。STRef を使うと、可変配列に対する STRef を受け取ってコピーを一切避けることができる。さらに、僕の命令形のアクションは第一級となるのでいつものコンビネータを使って合成することができるようになる。

これは面白い点だ。可変状態が漏洩しないことが保証されているため、データのコピーをせずに可変状態の変化を連鎖して合成することができる。可変状態が必要な場合の多くは配列が必要な場合が多い。そのため STArray という配列へのラッパーがある:

sealed trait STArray[S, A] {
  val size: Int
  val z: A
  private val value: Array[A] = Array.fill(size)(z)
  /**Reads the value at the given index. */
  def read(i: Int): ST[S, A] = returnST(value(i))
  /**Writes the given value to the array, at the given offset. */
  def write(i: Int, a: A): ST[S, STArray[S, A]] = ...
  /**Turns a mutable array into an immutable one which is safe to return. */
  def freeze: ST[S, ImmutableArray[A]] = ...
  /**Fill this array from the given association list. */
  def fill[B](f: (A, B) => A, xs: Traversable[(Int, B)]): ST[S, Unit] = ...
  /**Combine the given value with the value at the given index, using the given function. */
  def update[B](f: (A, B) => A, i: Int, v: B) = ...
}

これは ST.newArr(size: Int, z: A を用いて作られる。エラトステネスのふるいを使って 1000 以下の全ての素数を計算してみよう…

速報

STArray にバグを見つけたので、さっさと直すことにする:

$ git pull --rebase
Current branch scalaz-seven is up to date.
$ git branch topic/starrayfix
$ git co topic/starrayfix
Switched to branch 'topic/starrayfix'

ST にスペックが無いので、バグを再現するためにもスペックを書き起こすことにする。これで誰かが僕の修正を戻してもバグが捕獲できる。

package scalaz
package effect

import std.AllInstances._
import ST._

class STTest extends Spec {
  type ForallST[A] = Forall[({type λ[S] = ST[S, A]})#λ]

  "STRef" in {
    def e1[S] = for {
      x <- newVar[S](0)
      r <- x mod {_ + 1}
    } yield x
    def e2[S]: ST[S, Int] = for {
      x <- e1[S]
      r <- x.read
    } yield r
    runST(new ForallST[Int] { def apply[S] = e2[S] }) must be_===(1)
  }

  "STArray" in {
    def e1[S] = for {
      arr <- newArr[S, Boolean](3, true)
      _ <- arr.write(0, false)
      r <- arr.freeze
    } yield r
    runST(new ForallST[ImmutableArray[Boolean]] { def apply[S] = e1[S] }).toList must be_===(
      List(false, true, true))
  }
}

これが結果だ:

[info] STTest
[info] 
[info] + STRef
[error] ! STArray
[error]   NullPointerException: null (ArrayBuilder.scala:37)
[error] scala.collection.mutable.ArrayBuilder$.make(ArrayBuilder.scala:37)
[error] scala.Array$.newBuilder(Array.scala:52)
[error] scala.Array$.fill(Array.scala:235)
[error] scalaz.effect.STArray$class.$init$(ST.scala:71)
...

Scala で NullPointerException?! これは以下の STArray のコードからきている:

sealed trait STArray[S, A] {
  val size: Int
  val z: A
  implicit val manifest: Manifest[A]

  private val value: Array[A] = Array.fill(size)(z)
  ...
}
...
trait STArrayFunctions {
  def stArray[S, A](s: Int, a: A)(implicit m: Manifest[A]): STArray[S, A] = new STArray[S, A] {
    val size = s
    val z = a
    implicit val manifest = m
  }
}

見えたかな? Paulp さんがこれの FAQ を書いている。value が未初期化の size と z を使って初期化されている。以下が僕の加えた修正:

sealed trait STArray[S, A] {
  def size: Int
  def z: A
  implicit def manifest: Manifest[A]

  private lazy val value: Array[A] = Array.fill(size)(z)
  ...
}

これでテストは通過したので、push して pull request を送る。

Back to the usual programming

エラトステネスのふるいは素数を計算する簡単なアルゴリズムだ。

scala> import scalaz._, Scalaz._, effect._, ST._
import scalaz._
import Scalaz._
import effect._
import ST._

scala> def mapM[A, S, B](xs: List[A])(f: A => ST[S, B]): ST[S, List[B]] =
         Monad[({type λ[α] = ST[S, α]})#λ].sequence(xs map f)
mapM: [A, S, B](xs: List[A])(f: A => scalaz.effect.ST[S,B])scalaz.effect.ST[S,List[B]]

scala> def sieve[S](n: Int) = for {
         arr <- newArr[S, Boolean](n + 1, true)
         _ <- arr.write(0, false)
         _ <- arr.write(1, false)
         val nsq = (math.sqrt(n.toDouble).toInt + 1)
         _ <- mapM (1 |-> nsq) { i =>
           for {
             x <- arr.read(i)
             _ <-
               if (x) mapM (i * i |--> (i, n)) { j => arr.write(j, false) }
               else returnST[S, List[Boolean]] {Nil}
           } yield ()
         }
         r <- arr.freeze
       } yield r
sieve: [S](n: Int)scalaz.effect.ST[S,scalaz.ImmutableArray[Boolean]]

scala> type ForallST[A] = Forall[({type λ[S] = ST[S, A]})#λ]
defined type alias ForallST

scala> def prime(n: Int) =
         runST(new ForallST[ImmutableArray[Boolean]] { def apply[S] = sieve[S](n) }).toArray.
         zipWithIndex collect { case (true, x) => x }
prime: (n: Int)Array[Int]

scala> prime(1000)
res21: Array[Int] = Array(2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, ...

最初の 1000個の素数のリストによると、結果は大丈夫みたいだ。STArray の反復を理解するのが一番難しかった。ここでは ST[S, _] のコンテキスト内にいるから、ループの結果も ST モナドである必要がある。リストを投射して配列に書き込むとそれは List[ST[S, Unit]] を返してしまう。

ST[S, B] へのモナディック関数を受け取ってモナドを裏返して ST[S, List[B]] を返す mapM を実装した。sequence と基本的には同じだけど、こっちの方が感覚的に理解しやすいと思う。var を使うのと比べると苦労無しとは言い難いけど、可変のコンテキストを渡せるのは役に立つかもしれない。

続きはまた後で。

17日目

昨日は計算結果をキャッシュする方法としての Memo と、可変性をカプセル化する方法としての ST をみた。今日は続いて IO をみてみよう。

Daniel Steger for openphoto.net

IO モナド

論文の後半を読むかわりに Rúnar さん (@runarorama) の Towards an Effect System in Scala, Part 2: IO Monad を読もう:

While ST gives us guarantees that mutable memory is never shared, it says nothing about reading/writing files, throwing exceptions, opening network sockets, database connections, etc.

以下に ST の型クラスコントラクトをもう一度:

sealed trait ST[S, A] {
  private[effect] def apply(s: World[S]): (World[S], A)
}

そしてこれが IO の型クラスコントラクトだ:

sealed trait IO[+A] {
  private[effect] def apply(rw: World[RealWorld]): Trampoline[(World[RealWorld], A)]
}

Trampoline の部分を無視すると、IO は ST の状態を RealWorld に固定したものに似ている。ST 同様に IO object 下にある関数を使って IO モナドを作ることができる。

scala> import scalaz._, Scalaz._, effect._, IO._
import scalaz._
import Scalaz._
import effect._
import IO._

scala> val action1 = for {
         _ <- putStrLn("Hello, world!")
       } yield ()
action1: scalaz.effect.IO[Unit] = scalaz.effect.IOFunctions$$anon$4@149f6f65

scala> action1.unsafePerformIO
Hello, world!

以下が IO の下にある IO アクションだ:

  /** Reads a character from standard input. */
  def getChar: IO[Char] = ...
  /** Writes a character to standard output. */
  def putChar(c: Char): IO[Unit] = ...
  /** Writes a string to standard output. */
  def putStr(s: String): IO[Unit] = ...
  /** Writes a string to standard output, followed by a newline.*/
  def putStrLn(s: String): IO[Unit] = ...
  /** Reads a line of standard input. */
  def readLn: IO[String] = ...
  /** Write the given value to standard output. */
  def putOut[A](a: A): IO[Unit] = ...
  // Mutable variables in the IO monad
  def newIORef[A](a: => A): IO[IORef[A]] = ...
  /**Throw the given error in the IO monad. */
  def throwIO[A](e: Throwable): IO[A] = ...
  /** An IO action that does nothing. */
  val ioUnit: IO[Unit] = ...
}

IO object の apply メソッドを使って独自のアクションを作ることもできる:

scala> val action2 = IO {
         val source = scala.io.Source.fromFile("./README.md")
         source.getLines.toStream
       }
action2: scalaz.effect.IO[scala.collection.immutable.Stream[String]] = scalaz.effect.IOFunctions$$anon$4@bab4387

scala> action2.unsafePerformIO.toList
res57: List[String] = List(# Scalaz, "", Scalaz is a Scala library for functional programming., "", It provides purely functional data structures to complement those from the Scala standard library., ...

TESS2:

Composing these into programs is done monadically. So we can use for-comprehensions. Here’s a program that reads a line of input and prints it out again:

def program: IO[Unit] = for {
  line <- readLn
  _    <- putStrLn(line)
} yield ()

IO[Unit] is an instance of Monoid, so we can re-use the monoid addition function |+|.

試してみよう:

scala> (program |+| program).unsafePerformIO
123
123

Enumeration-Based I/O with Iteratees

IO を処理するもう 1つの方法に Iteratee と呼ばれるものがあり、最近にわかに注目を浴びている。Scalaz 5 の実装を Rúnar さんが解説した Scalaz Tutorial: Enumeration-Based I/O with Iteratees (EBIOI) があるけど、Scalaz 7 には新しい Iteratee が加わった。

とりあえず EBIOI を読んでみる:

Most programmers have come across the problem of treating an I/O data source (such as a file or a socket) as a data structure. This is a common thing to want to do. … Instead of implementing an interface from which we request Strings by pulling, we’re going to give an implementation of an interface that can receive Strings by pushing. And indeed, this idea is nothing new. This is exactly what we do when we fold a list:

def foldLeft[B](b: B)(f: (B, A) => B): B

Scalaz 7 のインターフェイスをみてみよう。以下が Input だ:

sealed trait Input[E] {
  def fold[Z](empty: => Z, el: (=> E) => Z, eof: => Z): Z
  def apply[Z](empty: => Z, el: (=> E) => Z, eof: => Z) =
    fold(empty, el, eof)
}

そしてこれが IterateeT:

sealed trait IterateeT[E, F[_], A] {
  def value: F[StepT[E, F, A]]
}
type Iteratee[E, A] = IterateeT[E, Id, A]

object Iteratee
  extends IterateeFunctions
  with IterateeTFunctions
  with EnumeratorTFunctions
  with EnumeratorPFunctions
  with EnumerateeTFunctions
  with StepTFunctions
  with InputFunctions {

  def apply[E, A](s: Step[E, A]): Iteratee[E, A] = iteratee(s)
}

type >@>[E, A] = Iteratee[E, A]

IterateeT はモナド変換子みたいだ。

EBIOI:

Let’s see how we would use this to process a List. The following function takes a list and an iteratee and feeds the list’s elements to the iteratee.

Iteratee object は enumerate その他を実装する EnumeratorTFunctions を継承するため、このステップは飛ばすことができる:

  def enumerate[E](as: Stream[E]): Enumerator[E] = ...
  def enumList[E, F[_] : Monad](xs: List[E]): EnumeratorT[E, F] = ...
  ...

これは以下のように定義された Enumerator[E] を返す:

trait EnumeratorT[E, F[_]] { self =>
  def apply[A]: StepT[E, F, A] => IterateeT[E, F, A]
  ...
}
type Enumerator[E] = EnumeratorT[E, Id]

EBIOI のカウンターの例題を実装してみよう。sbt から iteratee プロジェクトに切り替える:

$ sbt
scalaz> project iteratee
scalaz-iteratee> console
[info] Starting scala interpreter...

scala> import scalaz._, Scalaz._, iteratee._, Iteratee._
import scalaz._
import Scalaz._
import iteratee._
import Iteratee._

scala> def counter[E]: Iteratee[E, Int] = {
         def step(acc: Int)(s: Input[E]): Iteratee[E, Int] =
           s(el = e => cont(step(acc + 1)),
             empty = cont(step(acc)),
             eof = done(acc, eofInput[E])
           )
         cont(step(0))
       }
counter: [E]=> scalaz.iteratee.package.Iteratee[E,Int]

scala> (counter[Int] &= enumerate(Stream(1, 2, 3))).run
res0: scalaz.Id.Id[Int] = 3

このようなよく使われる演算は Iteratee object 下に畳み込み関数として用意されてある。だけど、IterateeT を念頭に書かれているので、Id モナドを型パラメータとして渡してやる必要がある:

scala> (length[Int, Id] &= enumerate(Stream(1, 2, 3))).run
res1: scalaz.Scalaz.Id[Int] = 3

drop と head は IterateeTFunctions の実装をみてみる:

  /**An iteratee that skips the first n elements of the input **/
  def drop[E, F[_] : Pointed](n: Int): IterateeT[E, F, Unit] = {
    def step(s: Input[E]): IterateeT[E, F, Unit] =
      s(el = _ => drop(n - 1),
        empty = cont(step),
        eof = done((), eofInput[E]))
    if (n == 0) done((), emptyInput[E])
    else cont(step)
  }

  /**An iteratee that consumes the head of the input **/
  def head[E, F[_] : Pointed]: IterateeT[E, F, Option[E]] = {
    def step(s: Input[E]): IterateeT[E, F, Option[E]] =
      s(el = e => done(Some(e), emptyInput[E]),
        empty = cont(step),
        eof = done(None, eofInput[E])
      )
    cont(step)
  }

Iteratee の合成

EBIOI:

In other words, iteratees compose sequentially.

以下が Scalaz 7 を使った drop1keep1 だ:

scala> def drop1Keep1[E]: Iteratee[E, Option[E]] = for {
         _ <- drop[E, Id](1)
         x <- head[E, Id]
       } yield x
drop1Keep1: [E]=> scalaz.iteratee.package.Iteratee[E,Option[E]]

渡された Monoid に累積する repeatBuild という関数があるので、alternates の Stream 版は以下のように書ける:

scala> def alternates[E]: Iteratee[E, Stream[E]] =
         repeatBuild[E, Option[E], Stream](drop1Keep1) map {_.flatten}
alternates: [E](n: Int)scalaz.iteratee.package.Iteratee[E,Stream[E]]

scala> (alternates[Int] &= enumerate(Stream.range(1, 15))).run.force
res7: scala.collection.immutable.Stream[Int] = Stream(2, 4, 6, 8, 10, 12, 14)

Iteratees を用いたファイル入力

EBIOI:

Using the iteratees to read from file input turns out to be incredibly easy.

java.io.Reader を処理するために Scalaz 7 には Iteratee.enumReader[F[_]](r: => java.io.Reader) 関数がついてくる。これで何故 Iteratee が IterateeT として実装されたのかという謎が解けた。そのまま IO を突っ込めるからだ:

scala> import scalaz._, Scalaz._, iteratee._, Iteratee._, effect._
import scalaz._
import Scalaz._
import iteratee._
import Iteratee._
import effect._

scala> import java.io._
import java.io._

scala> enumReader[IO](new BufferedReader(new FileReader("./README.md")))
res0: scalaz.iteratee.EnumeratorT[scalaz.effect.IoExceptionOr[Char],scalaz.effect.IO] = scalaz.iteratee.EnumeratorTFunctions$$anon$14@548ace66

最初の文字を得るには、以下のように head[IoExceptionOr[Char], IO] を実行する:

scala> (head[IoExceptionOr[Char], IO] &= res0).map(_ flatMap {_.toOption}).run.unsafePerformIO
res1: Option[Char] = Some(#)

EBIOI:

We can get the number of lines in two files combined, by composing two enumerations and using our “counter” iteratee from above.

これも試してみよう:

scala> def lengthOfTwoFiles(f1: File, f2: File) = {
         val l1 = length[IoExceptionOr[Char], IO] &= enumReader[IO](new BufferedReader(new FileReader(f1)))
         val l2 = l1 &= enumReader[IO](new BufferedReader(new FileReader(f2)))
         l2.run
       }

scala> lengthOfTwoFiles(new File("./README.md"), new File("./TODO.txt")).unsafePerformIO
res65: Int = 12731

IterateeUsage.scala には他にも面白そうな例がある:

scala> val readLn = takeWhile[Char, List](_ != '\n') flatMap (ln => drop[Char, Id](1).map(_ => ln))
readLn: scalaz.iteratee.IterateeT[Char,scalaz.Id.Id,List[Char]] = scalaz.iteratee.IterateeTFunctions$$anon$9@560ff23d

scala> (readLn &= enumStream("Iteratees\nare\ncomposable".toStream)).run
res67: scalaz.Id.Id[List[Char]] = List(I, t, e, r, a, t, e, e, s)

scala> (collect[List[Char], List] %= readLn.sequenceI &= enumStream("Iteratees\nare\ncomposable".toStream)).run
res68: scalaz.Id.Id[List[List[Char]]] = List(List(I, t, e, r, a, t, e, e, s), List(a, r, e), List(c, o, m, p, o, s, a, b, l, e))

上では sequenceI メソッドは readLn を EnumerateeT に変換して、%= はそれを Iteratee にチェインしている。

EBIOI:

So what we have here is a uniform and compositional interface for enumerating both pure and effectful data sources.

この文の意義を実感するにはもう少し時間がかかりそうだ。

リンク

Scalaz Tutorial: Enumeration-Based I/O with Iteratees
Iteratees。これは Josh Suereth さん (@jsuereth) による Iteratee。
Haskell wiki の Enumerator and iteratee。

18日目

17日目は、副作用を抽象化する方法としての IO モナドと、ストリームを取り扱うための Iteratee をみて、シリーズを終えた。

Func

Applicative 関数の合成を行うより良い方法を引き続き試してみて、AppFunc というラッパーを作った:

val f = AppFuncU { (x: Int) => x + 1 }
val g = AppFuncU { (x: Int) => List(x, 5) }
(f @&&& g) traverse List(1, 2, 3)

これを pull request として送った後、Lars Hupel さん (@larsr_h) から typelevel モジュールを使って一般化した方がいいという提案があったので、Func に拡張した:

/**
 * Represents a function `A => F[B]` where `[F: TC]`.
 */
trait Func[F[_], TC[F[_]] <: Functor[F], A, B] {
  def runA(a: A): F[B]
  implicit def TC: KTypeClass[TC]
  implicit def F: TC[F]
  ...
}

これを使うと、AppFunc は Func の 2つ目の型パラメータに Applicative を入れた特殊形という扱いになる。Lars さんはさらに合成を HList に拡張したいみたいだけど、いつかこの機能が Scalaz 7 に入ると楽観的に見ている。

この記事は Rúnar の助言に基づいて大幅に手を加えた。古い版は github のソースを参照してほしい。

Free Monad

今日は、Gabriel Gonzalez の Why free monads matter を読みながら Free モナドをみていく:

構文木の本質を表す抽象体を考えてみよう。[中略] 僕らの toy 言語には 3つのコマンドしかない:

output b -- prints a "b" to the console
bell     -- rings the computer's bell
done     -- end of execution

次のコマンドが前のコマンドの子ノードであるような構文木としてあらわしてみる:

data Toy b next =
    Output b next
  | Bell next
  | Done

とりあえずこれを素直に Scala に翻訳するとこうなる:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait Toy[+A, +Next]
case class Output[A, Next](a: A, next: Next) extends Toy[A, Next]
case class Bell[Next](next: Next) extends Toy[Nothing, Next]
case class Done() extends Toy[Nothing, Nothing]

// Exiting paste mode, now interpreting.

scala> Output('A', Done())
res0: Output[Char,Done] = Output(A,Done())

scala> Bell(Output('A', Done()))
res1: Bell[Output[Char,Done]] = Bell(Output(A,Done()))

CharToy

WFMM の DSL はアウトプット用のデータ型を型パラメータとして受け取るので、任意のアウトプット型を扱うことができる。上に Toy として示したように Scala も同じことができる。だけども、Scala の部分適用型の処理がヘボいため Free の説明としては不必要に複雑となってしまう。そのため、本稿では、以下のようにデータ型を Char に決め打ちしたものを使う:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait CharToy[+Next]
object CharToy {
  case class CharOutput[Next](a: Char, next: Next) extends CharToy[Next]
  case class CharBell[Next](next: Next) extends CharToy[Next]
  case class CharDone() extends CharToy[Nothing]

  def output[Next](a: Char, next: Next): CharToy[Next] = CharOutput(a, next)
  def bell[Next](next: Next): CharToy[Next] = CharBell(next)
  def done: CharToy[Nothing] = CharDone()
}

// Exiting paste mode, now interpreting.

scala> import CharToy._
import CharToy._

scala> output('A', done)
res0: CharToy[CharToy[Nothing]] = CharOutput(A,CharDone())

scala> bell(output('A', done))
res1: CharToy[CharToy[CharToy[Nothing]]] = CharBell(CharOutput(A,CharDone()))

型を CharToy に統一するため、小文字の output、bell、done を加えた。

Fix

WFMM:

しかし残念なことに、コマンドを追加するたびに型が変わってしまうのでこれはうまくいかない。

Fix を定義しよう:

scala> :paste
// Entering paste mode (ctrl-D to finish)

case class Fix[F[_]](f: F[Fix[F]])
object Fix {
  def fix(toy: CharToy[Fix[CharToy]]) = Fix[CharToy](toy)
}

// Exiting paste mode, now interpreting.

scala> import Fix._
import Fix._

scala> fix(output('A', fix(done)))
res4: Fix[CharToy] = Fix(CharOutput(A,Fix(CharDone())))

scala> fix(bell(fix(output('A', fix(done)))))
res5: Fix[CharToy] = Fix(CharBell(Fix(CharOutput(A,Fix(CharDone())))))

ここでも fix を提供して型推論が動作するようにした。

FixE

これに例外処理を加えた FixE も実装してみる。throw と catch は予約語なので、throwy、catchy という名前に変える:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait FixE[F[_], E]
object FixE {
  case class Fix[F[_], E](f: F[FixE[F, E]]) extends FixE[F, E]
  case class Throwy[F[_], E](e: E) extends FixE[F, E]   

  def fix[E](toy: CharToy[FixE[CharToy, E]]): FixE[CharToy, E] =
  　Fix[CharToy, E](toy)
  def throwy[F[_], E](e: E): FixE[F, E] = Throwy(e)
  def catchy[F[_]: Functor, E1, E2](ex: => FixE[F, E1])
  　　(f: E1 => FixE[F, E2]): FixE[F, E2] = ex match {
    case Fix(x)    => Fix[F, E2](Functor[F].map(x) {catchy(_)(f)})
    case Throwy(e) => f(e)
  }
}

// Exiting paste mode, now interpreting.

これを実際に使うには Toy b が functor である必要があるので、型検査が通るまで色々試してみる (Functor則を満たす必要もある)。

CharToy の Functor はこんな感じになった:

scala> implicit val charToyFunctor: Functor[CharToy] = new Functor[CharToy] {
         def map[A, B](fa: CharToy[A])(f: A => B): CharToy[B] = fa match {
           case o: CharOutput[A] => CharOutput(o.a, f(o.next))
           case b: CharBell[A]   => CharBell(f(b.next))
           case CharDone()       => CharDone()
         }
       }
charToyFunctor: scalaz.Functor[CharToy] = $anon$1@7bc135fe

これがサンプルの使用例だ:

scala> :paste
// Entering paste mode (ctrl-D to finish)

import FixE._
case class IncompleteException()
def subroutine = fix[IncompleteException](
  output('A', 
    throwy[CharToy, IncompleteException](IncompleteException())))
def program = catchy[CharToy, IncompleteException, Nothing](subroutine) { _ =>
  fix[Nothing](bell(fix[Nothing](done)))
}

型パラメータでゴテゴテになってるのはちょっと残念な感じだ。

Free monads part 1

WFMM:

僕らの FixE は既に存在していて、それは Free モナドと呼ばれる:

data Free f r = Free (f (Free f r)) | Pure r

名前の通り、これは自動的にモナドだ (ただし、f が Functor の場合)

instance (Functor f) => Monad (Free f) where
    return = Pure
    (Free x) >>= f = Free (fmap (>>= f) x)
    (Pure r) >>= f = f r

これに対応する Scalaz でのデータ構造は Free と呼ばれる:

sealed abstract class Free[S[+_], +A](implicit S: Functor[S]) {
  final def map[B](f: A => B): Free[S, B] =
    flatMap(a => Return(f(a)))

  final def flatMap[B](f: A => Free[S, B]): Free[S, B] = this match {
    case Gosub(a, g) => Gosub(a, (x: Any) => Gosub(g(x), f))
    case a           => Gosub(a, f)
  }
  ...
}

object Free extends FreeInstances {
  /** Return from the computation with the given value. */
  case class Return[S[+_]: Functor, +A](a: A) extends Free[S, A]

  /** Suspend the computation with the given suspension. */
  case class Suspend[S[+_]: Functor, +A](a: S[Free[S, A]]) extends Free[S, A]

  /** Call a subroutine and continue with the given function. */
  case class Gosub[S[+_]: Functor, A, +B](a: Free[S, A],
                                          f: A => Free[S, B]) extends Free[S, B]
}

trait FreeInstances {
  implicit def freeMonad[S[+_]:Functor]: Monad[({type f[x] = Free[S, x]})#f] =
    new Monad[({type f[x] = Free[S, x]})#f] {
      def point[A](a: => A) = Return(a)
      override def map[A, B](fa: Free[S, A])(f: A => B) = fa map f
      def bind[A, B](a: Free[S, A])(f: A => Free[S, B]) = a flatMap f
    }
}

Scalaz 版では、Free コンストラクタは Free.Suspend と呼ばれ、Pure は Free.Return と呼ばれる。 CharToy コマンドを Free を使って再実装する:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait CharToy[+Next]
object CharToy {
  case class CharOutput[Next](a: Char, next: Next) extends CharToy[Next]
  case class CharBell[Next](next: Next) extends CharToy[Next]
  case class CharDone() extends CharToy[Nothing]

  implicit val charToyFunctor: Functor[CharToy] = new Functor[CharToy] {
    def map[A, B](fa: CharToy[A])(f: A => B): CharToy[B] = fa match {
        case o: CharOutput[A] => CharOutput(o.a, f(o.next))
        case b: CharBell[A]   => CharBell(f(b.next))
        case CharDone()       => CharDone()
      }
    }

  def output(a: Char): Free[CharToy, Unit] =
    Free.Suspend(CharOutput(a, Free.Return[CharToy, Unit](())))
  def bell: Free[CharToy, Unit] =
    Free.Suspend(CharBell(Free.Return[CharToy, Unit](())))
  def done: Free[CharToy, Unit] = Free.Suspend(CharDone())
}

// Exiting paste mode, now interpreting.

defined trait CharToy
defined module CharToy

これは、さすがに共通パターンを抽出できるはず。

liftF をつかったリファクタリングも行う。あと、return に相当するものが必要なので、pointed も定義する:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait CharToy[+Next]
object CharToy {
  case class CharOutput[Next](a: Char, next: Next) extends CharToy[Next]
  case class CharBell[Next](next: Next) extends CharToy[Next]
  case class CharDone() extends CharToy[Nothing]

  implicit val charToyFunctor: Functor[CharToy] = new Functor[CharToy] {
    def map[A, B](fa: CharToy[A])(f: A => B): CharToy[B] = fa match {
        case o: CharOutput[A] => CharOutput(o.a, f(o.next))
        case b: CharBell[A]   => CharBell(f(b.next))
        case CharDone()       => CharDone()
      }
    }
  private def liftF[F[+_]: Functor, R](command: F[R]): Free[F, R] =
    Free.Suspend[F, R](Functor[F].map(command) { Free.Return[F, R](_) })
  def output(a: Char): Free[CharToy, Unit] =
    liftF[CharToy, Unit](CharOutput(a, ()))
  def bell: Free[CharToy, Unit] = liftF[CharToy, Unit](CharBell(()))
  def done: Free[CharToy, Unit] = liftF[CharToy, Unit](CharDone())
  def pointed[A](a: A) = Free.Return[CharToy, A](a)
}

// Exiting paste mode, now interpreting.

コマンドのシーケンスはこんな感じになる:

scala> import CharToy._
import CharToy._

scala> val subroutine = output('A')
subroutine: scalaz.Free[CharToy,Unit] = Suspend(CharOutput(A,Return(())))

scala> val program = for {
         _ <- subroutine
         _ <- bell
         _ <- done
       } yield ()
program: scalaz.Free[CharToy,Unit] = Gosub(<function0>,<function1>)

面白くなってきた。「まだ評価されていないもの」に対する do 記法を得られることができた。これは純粋なデータだ。

次に、これが本当に純粋なデータであることを証明するために showProgram を定義する。WFMM は単純なパターンマッチングを使って showProgram を定義するけども、この Free はちょっとそのままでうまくいかない。flatMap の定義をみてほしい:

  final def flatMap[B](f: A => Free[S, B]): Free[S, B] = this match {
    case Gosub(a, g) => Gosub(a, (x: Any) => Gosub(g(x), f))
    case a           => Gosub(a, f)
  }

新しい Return や Suspend を計算する代わりに Gosub というデータ構造を作っている。この Gosub を評価して \/ を返す resume メソッドがあるので、showProgram は以下のように実装できる:

scala> def showProgram[R: Show](p: Free[CharToy, R]): String =
         p.resume.fold({
           case CharOutput(a, next) =>
             "output " + Show[Char].shows(a) + "\n" + showProgram(next)
           case CharBell(next) =>
             "bell " + "\n" + showProgram(next)
           case CharDone() =>
             "done\n"
         },
         { r: R => "return " + Show[R].shows(r) + "\n" }) 
showProgram: [R](p: scalaz.Free[CharToy,R])(implicit evidence$1: scalaz.Show[R])String

scala> showProgram(program)
res12: String = 
"output A
bell 
done
"

pretty printer はこうなる:

scala> def pretty[R: Show](p: Free[CharToy, R]) = print(showProgram(p))
pretty: [R](p: scalaz.Free[CharToy,R])(implicit evidence$1: scalaz.Show[R])Unit

scala> pretty(output('A'))
output A
return ()

さて、真実の時だ。Free を使って生成したモナドはモナド則を満たしているだろうか?

scala> pretty(output('A'))
output A
return ()

scala> pretty(pointed('A') >>= output)
output A
return ()

scala> pretty(output('A') >>= pointed)
output A
return ()

scala> pretty((output('A') >> done) >> output('C'))
output A
done

scala> pretty(output('A') >> (done >> output('C')))
output A
done

うまくいった。done が abort的な意味論になっていることにも注目してほしい。

Free monads part 2

WFMM:

data Free f r = Free (f (Free f r)) | Pure r
data List a   = Cons  a (List a  )  | Nil

言い換えると、Free モナドは Functor のリストだと考えることができる。Free コンストラクタは Cons のように振る舞い Functor をリストの先頭に追加し、Pure コンストラクタは Nil のように振る舞い空のリストを表す (つまり Functor が無い状態だ)。

第三部。

Free monads part 3

WFMM:

Free モナドはインタプリタの良き友だ。Free モナドはインタプリタを限りなく「解放 (free) 」しつつも必要最低限のモナドの条件を満たしている。

逆に、プログラムを書いている側から見ると、Free モナドそのものは逐次化以外の何も提供しない。インタプリタが何らかの run 関数を提供して役に立つ機能が得られる。ポイントは、Functor を満たすデータ構造さえあれば Free が最小のモナドを自動的に提供してくれることだと思う。

もう一つの見方としては、Free は与えられたコンテナを使って構文木を作る方法を提供する。

Stackless Scala with Free Monads

Free モナドに関する一般的な理解が得られた所で、Scala Days 2012 での Rúnar の講演を観よう: Stackless Scala With Free Monads。ペーパーを読む前にトークを観ておくことをお勧めするけど、ペーパーの方が引用しやすいので Stackless Scala With Free Monads もリンクしておく。

Rúnar はまず State モナドを使ってリストに添字を zip するコードから始める。これはリストがスタックの限界よりも大きいと、スタックを吹っ飛ばす。続いてプログラム全体を一つのループで回すトランポリンというものを紹介している。

sealed trait Trampoline [+ A] {
  final def runT : A =
    this match {
      case More (k) => k().runT
      case Done (v) => v
    }
}
case class More[+A](k: () => Trampoline[A])
  extends Trampoline[A]
case class Done [+A](result: A)
  extends Trampoline [A]

上記のコードでは Function0 の k は次のステップのための thunk となっている。

これを State モナドを使った使用例に拡張するため、flatMap を FlatMap というデータ構造に具現化している:

case class FlatMap [A,+B](
  sub: Trampoline [A],
  k: A => Trampoline[B]) extends Trampoline[B]

続いて、Trampoline は実は Function0 の Free モナドであることが明かされる。Scalaz 7 では以下のように定義されている:

  type Trampoline[+A] = Free[Function0, A]

Free monads

さらに Rúnar は便利な Free モナドを作れるいくつかのデータ構造を紹介する:

type Pair[+A] = (A, A)
type BinTree[+A] = Free[Pair, A]

type Tree[+A] = Free[List, A]

type FreeMonoid[+A] = Free[({type λ[+α] = (A,α)})#λ, Unit]

type Trivial[+A] = Unit
type Option[+A] = Free[Trivial, A]

Free モナドを使った Iteratee まであるみたいだ。最後に Free モナドを以下のようにまとめている:

データが末端に来る全ての再帰データ型に使えるモデル
Free モナドは変数が末端にある式木で、flatMap は変数の置換にあたる。

トランポリン

トランポリンを使えば、どんなプログラムでもスタックを使わないものに変換することができる。トークに出てきた even と odd を Scalaz 7 の Trampoline を使って実装してみよう。Free object はトランポリン化に役立つ関数を定義する FreeFunction を継承する:

trait FreeFunctions {
  /** Collapse a trampoline to a single step. */
  def reset[A](r: Trampoline[A]): Trampoline[A] = { val a = r.run; return_(a) }

  /** Suspend the given computation in a single step. */
  def return_[S[+_], A](value: => A)(implicit S: Pointed[S]): Free[S, A] =
    Suspend[S, A](S.point(Return[S, A](value)))

  def suspend[S[+_], A](value: => Free[S, A])(implicit S: Pointed[S]): Free[S, A] =
    Suspend[S, A](S.point(value))

  /** A trampoline step that doesn't do anything. */
  def pause: Trampoline[Unit] =
    return_(())

  ...
}

これらを使うには import Free._ を呼ぶ。

scala> import Free._
import Free._

scala> :paste
// Entering paste mode (ctrl-D to finish)

def even[A](ns: List[A]): Trampoline[Boolean] =
  ns match {
    case Nil => return_(true)
    case x :: xs => suspend(odd(xs))
  }
def odd[A](ns: List[A]): Trampoline[Boolean] =
  ns match {
    case Nil => return_(false)
    case x :: xs => suspend(even(xs))
  }

// Exiting paste mode, now interpreting.

even: [A](ns: List[A])scalaz.Free.Trampoline[Boolean]
odd: [A](ns: List[A])scalaz.Free.Trampoline[Boolean]

scala> even(List(1, 2, 3)).run
res118: Boolean = false

scala> even(0 |-> 3000).run
res119: Boolean = false

これは意外と簡単にできた。

Free を用いたリスト

Free を使って「リスト」を定義してみよう。

scala> type FreeMonoid[A] = Free[({type λ[+α] = (A,α)})#λ, Unit]
defined type alias FreeMonoid

scala> def cons[A](a: A): FreeMonoid[A] = Free.Suspend[({type λ[+α] = (A,α)})#λ, Unit]((a, Free.Return[({type λ[+α] = (A,α)})#λ, Unit](())))
cons: [A](a: A)FreeMonoid[A]

scala> cons(1)
res0: FreeMonoid[Int] = Suspend((1,Return(())))

scala> cons(1) >>= {_ => cons(2)}
res1: scalaz.Free[[+α](Int, α),Unit] = Gosub(Suspend((1,Return(()))),<function1>)

この結果を処理する一例として標準の List に変換してみる:

scala> def toList[A](list: FreeMonoid[A]): List[A] =
         list.resume.fold(
           { case (x: A, xs: FreeMonoid[A]) => x :: toList(xs) },
           { _ => Nil })

scala> toList(res1)
res4: List[Int] = List(1, 2)

今日はここまで。

19日目

Scalaz や Haskell の基礎となっている Monoid や Functor などの概念が圏論に由来することは周知のとおりだ。少し圏論を勉強してみて、その知識を Scalaz の理解を深めるの役立てられるか試してみよう。

圏論

僕が見た限りで最も取っ付きやすい圏論の本は Lawvere と Schanuel 共著の Conceptual Mathematics: A First Introduction to Categories 第二版だ。この本は普通の教科書のように書かれた Article という部分と Session と呼ばれる質疑や議論を含めた授業を書き取ったような解説の部分を混ぜた構成になっている。

Article の部分でも他の本と比べて基本的な概念に多くのページをさいて丁寧に解説しているので、独習者向けだと思う。

集合、射、射の合成

Conceptual Mathematics (以下 CM) の和訳が無いみたいなので、僕の勝手訳になる。訳語の選択などを含め @9_ties の2013年圏論勉強会資料を参考にした。この場を借りてお礼します:

「圏」(category) の正確な定義を与える前に、有限集合と射という圏の一例にまず慣れ親しむべきだ。この圏の対象 (object) は有限集合 (finite set) 別名 collection だ。 … 恐らくこのような有限集合の表記法を見たことがあるだろう:

{ John, Mary, Sam }

これは Scala だと 2通りの方法で表現できると思う。まずは a: Set[Person] という値を使った方法:

scala> :paste

sealed trait Person {}
case object John extends Person {}
case object Mary extends Person {}
case object Sam extends Person {}

val a: Set[Person] = Set[Person](John, Mary, Sam)

// Exiting paste mode, now interpreting.

もう一つの考え方は、Person という型そのものが Set を使わなくても既に有限集合となっていると考えることだ。注意: CM では map という用語を使っているけども、Mac Lane や他の本に合わせて本稿では arrow を英語での用語として採用する。

この圏の射 (arrow) f は以下の3つから構成される
集合 A。これは射のドメイン (domain) と呼ばれる。
集合 B。これは射のコドメイン (codomain) と呼ばれる。
ドメイン内のそれぞれの要素 (element, 元とも言う) a に対してコドメイン内の元 b を割り当てるルール。この b は f ∘ a (または f(a)) と表記され、「f　マル a」と読む。
(射の他にも「矢」、「写像」(map)、「函数」(function)、「変換」(transformation)、「作用素」(operator)、morphism などの言葉が使われることもある。)

好みの朝食の射を実装してみよう。

scala> :paste

sealed trait Breakfast {}
case object Eggs extends Breakfast {}
case object Oatmeal extends Breakfast {}
case object Toast extends Breakfast {}
case object Coffee extends Breakfast {}

val favoriteBreakfast: Person => Breakfast = {
  case John => Eggs
  case Mary => Coffee
  case Sam  => Coffee
}

// Exiting paste mode, now interpreting.

favoriteBreakfast: Person => Breakfast = <function1>

この圏の「対象」は Set[Person] か Person であるのに対して、「射」の favoriteBreakfast は型が Person である値を受け取ることに注意してほしい。以下がこの射の内部図式 (internal diagram) だ。
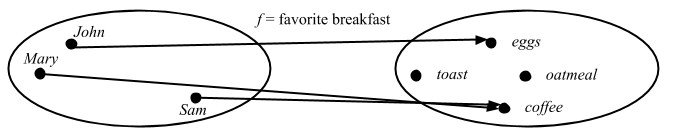
favorite breakfast

大切なのは、ドメイン内のそれぞれの黒丸から正確に一本の矢印が出ていて、その矢印がコドメイン内の何らかの黒丸に届いていることだ。

射が Function1[A, B] よりも一般的なものだということは分かるが、この圏の場合はこれで十分なので良しとする。これが favoritePerson の実装となる:

scala> val favoritePerson: Person => Person = {
         case John => Mary
         case Mary => John
         case Sam  => Mary
       }
favoritePerson: Person => Person = <function1>

ドメインとコドメインが同一の対象の射を自己準同型射 (endomorphism) と呼ぶ。

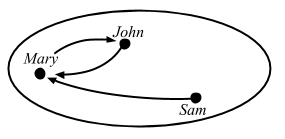
favorite person

ドメインとコドメインが同一の集合 A で、かつ A 内の全ての a において f(a) = a であるものを恒等射 (identity arrow) と言う。

「A の恒等射」は 1_A と表記する。
identity arrow

恒等射は射であるため、集合そのものというよりは集合の要素にはたらく。そのため、scala.Predef.identity を使うことができる。

scala> identity(John)
res0: John.type = John

上の 3つの内部図式に対応した外部図式 (external diagram) を見てみよう。
external diagrams

この図式を見て再び思うのは有限集合という圏においては、「対象」は Person や Breakfast のような型に対応して、射は Person => Person のような関数に対応するということだ。外部図式は Person => Person というような型レベルでのシグネチャに似ている。

圏の概念の最後の基礎部品で、圏の変化を全て担っているのが射の合成 (composition of maps) だ。これによって 2つの射を組み合わせて 3つ目の射を得ることができる。

Scala なら scala.Function1 の andThen か compose を使うことができる。

scala> val favoritePersonsBreakfast = favoriteBreakfast compose favoritePerson
favoritePersonsBreakfast: Person => Breakfast = <function1>

これが内部図式だ:
composition of arrows

そして外部図式:
external diagram: composition of arrows

射を合成すると外部図式はこうなる:
external diagram: f of g

’f ∘ g’ は「f マル g」、または「f と g の合成射」と読む。

圏のデータは以下の4部品から構成される:

対象 (objects): A, B, C, …
射 (arrows): f: A => B
恒等射 (identity arrows): 1_A: A => A
射の合成

これらのデータは以下の法則を満たさなければいけない:

単位元律 (The identity laws):

If 1_A: A => A, g: A => B, then g ∘ 1_A = g
If f: A => B, 1_B: B => B, then 1_A ∘ f = f

結合律 (The associative law):

If f: A => B, g: B => C, h: C => D, then h ∘ (g ∘ f) = (h ∘ g) ∘ f

点

CM:

単集合 (singleton) という非常に便利な集合あって、これは唯一の要素 (element; 元とも) のみを持つ。これを例えば {me} という風に固定して、この集合を 1 と呼ぶ。

定義: ある集合の点 (point) は、1 => X という射だ。
(もし A が既に親しみのある集合なら、A から X への射を X の「A-要素」という。そのため、「1-要素」は点となる。) 点は射であるため、他の射と合成して再び点を得ることができる。

誤解していることを恐れずに言えば、CM は要素という概念を射の特殊なケースとして再定義しているように思える。単集合 (singleton) の別名に unit set というものがあって、Scala では (): Unit となる。つまり、値は Unit => X の糖衣構文だと言っているのに類似している。

scala> val johnPoint: Unit => Person = { case () => John } 
johnPoint: Unit => Person = <function1>

scala> favoriteBreakfast compose johnPoint
res1: Unit => Breakfast = <function1>

scala> res1(())
res2: Breakfast = Eggs

関数型プログラミングをサポートする言語における第一級関数は、関数を値として扱うことで高階関数を可能とする。圏論は逆方向に統一して値を関数として扱っている。

Session 2 と 3 は Article I の復習を含むため、本を持っている人は是非読んでほしい。

集合の射の等価性

Session で面白いなと思った所があって、それは射の等価性に関しての話だ。圏論での問題の多くが射の等価性に関連するけども、f と g が等価であるかをどうやってテストしたらいいだろうか?

2つの射は 3つの材料が同一である場合に等価であると言える。

ドメイン A
コドメイン B
f ∘ a を割り当てるルール

1 のために、集合の射 f: A => B と g: A => B の等価性に関しては以下のように検証できる:

もしも各点 a: 1 => A に対して f ∘ a = g ∘ a である場合、f = g となる。

これで scalacheck を思い出したので、f: Person => Breakfast のチェックを実装してみる。

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait Person {}
case object John extends Person {}
case object Mary extends Person {}
case object Sam extends Person {}

sealed trait Breakfast {}
case object Eggs extends Breakfast {}
case object Oatmeal extends Breakfast {}
case object Toast extends Breakfast {}
case object Coffee extends Breakfast {}

val favoriteBreakfast: Person => Breakfast = {
  case John => Eggs
  case Mary => Coffee
  case Sam  => Coffee
}

val favoritePerson: Person => Person = {
  case John => Mary
  case Mary => John
  case Sam  => Mary
}

val favoritePersonsBreakfast = favoriteBreakfast compose favoritePerson

// Exiting paste mode, now interpreting.

scala> import org.scalacheck.{Prop, Arbitrary, Gen}
import org.scalacheck.{Prop, Arbitrary, Gen}

scala> def arrowEqualsProp(f: Person => Breakfast, g: Person => Breakfast)
         (implicit ev1: Equal[Breakfast], ev2: Arbitrary[Person]): Prop =
         Prop.forAll { a: Person =>
           f(a) === g(a)
         } 
arrowEqualsProp: (f: Person => Breakfast, g: Person => Breakfast)
(implicit ev1: scalaz.Equal[Breakfast], implicit ev2: org.scalacheck.Arbitrary[Person])org.scalacheck.Prop

scala> implicit val arbPerson: Arbitrary[Person] = Arbitrary {
         Gen.oneOf(John, Mary, Sam)
       }
arbPerson: org.scalacheck.Arbitrary[Person] = org.scalacheck.Arbitrary$$anon$2@41ec9951

scala> implicit val breakfastEqual: Equal[Breakfast] = Equal.equalA[Breakfast]
breakfastEqual: scalaz.Equal[Breakfast] = scalaz.Equal$$anon$4@783babde

scala> arrowEqualsProp(favoriteBreakfast, favoritePersonsBreakfast)
res0: org.scalacheck.Prop = Prop

scala> res0.check
! Falsified after 1 passed tests.
> ARG_0: John

scala> arrowEqualsProp(favoriteBreakfast, favoriteBreakfast)
res2: org.scalacheck.Prop = Prop

scala> res2.check
+ OK, passed 100 tests.

arrowEqualsProp をもう少し一般化してみる:

scala> def arrowEqualsProp[A, B](f: A => B, g: A => B)
         (implicit ev1: Equal[B], ev2: Arbitrary[A]): Prop =
         Prop.forAll { a: A =>
           f(a) === g(a)
         } 
arrowEqualsProp: [A, B](f: A => B, g: A => B)
(implicit ev1: scalaz.Equal[B], implicit ev2: org.scalacheck.Arbitrary[A])org.scalacheck.Prop

scala> arrowEqualsProp(favoriteBreakfast, favoriteBreakfast)
res4: org.scalacheck.Prop = Prop

scala> res4.check
+ OK, passed 100 tests.

同型射

CM:

定義: ある射 f: A => B に対して g ∘ f = 1_A と f ∘ g = 1_B の両方を満たす射 g: B => A が存在するとき、f を同型射 (isomorphism) または可逆な射 (invertible arrow) であるという。また、1つでも同型射 f: A => B が存在するとき、2つの対象 A と B は同型 (isomorphic) であるという。

Scalaz ではこれを Isomorphism 内で定義される trait を使って表す:

sealed abstract class Isomorphisms extends IsomorphismsLow0{
  /**Isomorphism for arrows of kind * -> * -> * */
  trait Iso[Arr[_, _], A, B] {
    self =>
    def to: Arr[A, B]
    def from: Arr[B, A]
  }

  /**Set isomorphism */
  type IsoSet[A, B] = Iso[Function1, A, B]

  /**Alias for IsoSet */
  type <=>[A, B] = IsoSet[A, B]
}

object Isomorphism extends Isomorphisms

より高いカインドの同型射も含むが、今のところは IsoSet で十分だ。

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait Family {}
case object Mother extends Family {}
case object Father extends Family {}
case object Child extends Family {}

sealed trait Relic {}
case object Feather extends Relic {}
case object Stone extends Relic {}
case object Flower extends Relic {}

import Isomorphism.<=>
val isoFamilyRelic = new (Family <=> Relic) {
  val to: Family => Relic = {
    case Mother => Feather
    case Father => Stone
    case Child  => Flower
  }
  val from: Relic => Family = {
    case Feather => Mother
    case Stone   => Father
    case Flower  => Child
  }
}

isoFamilyRelic: scalaz.Isomorphism.<=>[Family,Relic]{val to: Family => Relic; val from: Relic => Family} = 1@12e3914c

Scalaz に同型射を見つけたのは心強い。多分僕たちが正しい方向に向かっているということだと思う。

記法: もし f: A => B に (一意に定まる) 逆射 (inverse) があるとき、f の逆射は f^-1 と表記する。(読みは「f インバース」または「f の逆射」)

上の isoFamilyRelic が定義を満たすかを arrowEqualsProp で確かめることができる:

scala> :paste
// Entering paste mode (ctrl-D to finish)

implicit val familyEqual = Equal.equalA[Family]
implicit val relicEqual = Equal.equalA[Relic]
implicit val arbFamily: Arbitrary[Family] = Arbitrary {
  Gen.oneOf(Mother, Father, Child)
}
implicit val arbRelic: Arbitrary[Relic] = Arbitrary {
  Gen.oneOf(Feather, Stone, Flower)
}

// Exiting paste mode, now interpreting.

scala> arrowEqualsProp(isoFamilyRelic.from compose isoFamilyRelic.to, identity[Family] _)
res22: org.scalacheck.Prop = Prop

scala> res22.check
+ OK, passed 100 tests.

scala> arrowEqualsProp(isoFamilyRelic.to compose isoFamilyRelic.from, identity[Relic] _)
res24: org.scalacheck.Prop = Prop

scala> res24.check
+ OK, passed 100 tests.

決定問題と選択問題

CM:

1. 決定問題 (determination problem; もしくは extension)
図に表す f と g があるとき、h = g ∘ f が成り立つ g があれば全て挙げよ。

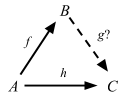
determination

2. 選択問題 (choice problem; もしくは lifting)
図に表す g と h があるとき、h = g ∘ f が成り立つ g があれば全て挙げよ。

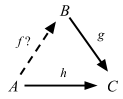
choice

これら 2つの問題は割り算に類似している。

レトラクションとセクション

定義: f: A => B があるとき、
r ∘ f = 1_A が成り立つ射 r: B => A をf のレトラクション (retraction) という。
f ∘ s = 1_B が成り立つ射 s: B => A をf のセクション (section) という。

レトラクション問題の外部図式はこうなる:

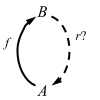
retraction

セクション問題の外部図式:

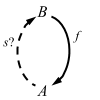
section

全射

もし射 f: A => B に関して「任意の射 y: T => B に対して f ∘ x = y が成り立つ射 x: T => A が存在する」という条件が成り立つ場合、「f は T からの射に関して全射 (surjective) である」という。

まずは集合論で全射 (surjective) と言ったときどういう意味なのかを考えるのに独自の例を作ってみた: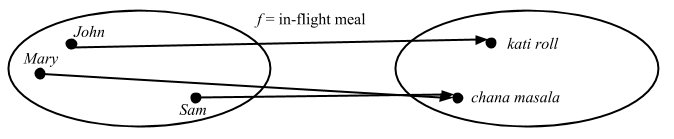

John が友達とインドに行くとして、飛行機の昼食に二つの選択があるとする: チキンラップサンドかスパイシーなヒヨコ豆だ。全射ということは各メニューに対して最低一人はその選択を選んだ人がいるということだ。言い換えると、コドメイン内の要素が網羅されている。

ここで単集合を導入することで要素という考えを一般化できることを思い出してほしい。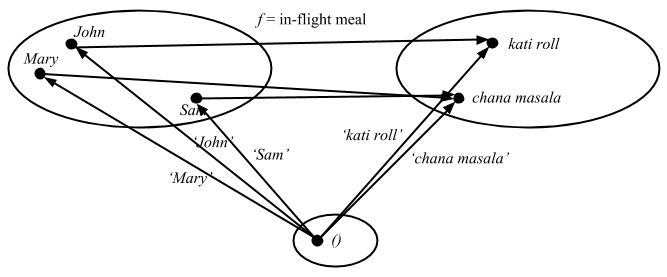
surjective with singleton

これを圏論での全射の定義と比較してみよう: 任意の射 y: T => B に対して f ∘ x = y が成り立つ射 x: T => A が存在する。どの 1 から B (昼食) への射に対しても、f ∘ x = y が成立する 1 から A (人) への射が存在する。つまり、f は 1 からの射に関して全射であると言える。

これを外部図式で表してみる。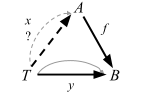
surjective external diagram
選択問題と同じ形になった。

単射とモノ射

定義: もし射 f に関して「任意の射のペア x₁: T => A と x₂: T => A に対して f ∘ x₁ = f ∘ x₂ ならば x₁ = x₂ である」という条件が成り立つ場合、「f は T からの射に関して単射 (injective) である」という。
もし f が全ての T からの射に関して単射である場合、f は単射である、またはモノ射 (monomorphism) であるという。

集合論で考えた場合の単射はこうなる:
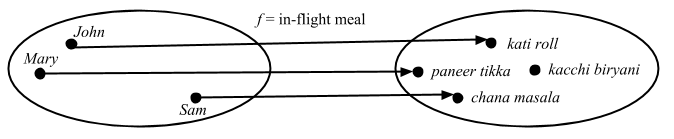
injective

コドメイン内の要素は全て一度だけ写像されている。ここで 3つ目の対象 T を頭の中で想像して、そこから John、Mary、Sam への射が出ているとする。どの射を合成してもユニークな食事へと届くはずだ。外部図式だとこうなる: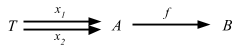
monomorphism

エピ射

定義: もし射 f に関して「任意の射のペア t₁: T => A と t₂: T => A に対して t₁ ∘ f = t₂ ∘ f ならば t₁ = t₂ である」という条件が全ての T において成り立つ場合、エピ射 (epimorphism) であるという。

これは全射の一般形らしいけども、本ではそこの所をつっこんでないので飛ばすことにする。

冪等射

定義: 自己準同型射 (endomorphism) について e ∘ e = e が成り立つとき冪等射 (idempotent) という。

冪等の読みはベキトウ。

自己同型射

自己準同型 (endomorphism) であり、かつ同型 (isomorphism) である射のことを自己同型射 (automorphism) という。

結構進めたので、これぐらいにしておこう。圏という考えが一度内部図式にバラすことで分かりやすくなったと思う。

20日目

19日目は Lawvere と Schanuel の『Conceptual Mathematics: A First Introduction to Categories』を使って圏論の基本となる概念をみてきた。この本は、基本的な概念の説明に具体例を使って多くのページを割いているので「圏」という概念の入門には向いてると思う。ただ、より高度な概念に進もうとしたときには、周りくどく感じてしまう。

Awodey の『Category Theory』

今日からは Steve Awodey氏の Category Theory に変えることにする。これは2013年圏論勉強会でも使われたものだ。この本も数学者じゃない人向けに書かれているけども、もう少し速いペースで進むし、抽象的思考に重点を置いている。

定義や定理が圏論的な概念のみに基づいていて、対象や射に関する追加の情報によらないとき、それらは抽象的 (abstract) であるという。抽象的な概念の利点は、即座にそれが全ての圏に適用できることだ。

定義 1.3 任意の圏 C において、ある射 f: A => B に対して以下の条件を満たす g: B => A が C 内にあるとき、その射は同型射 (isomorphism) であるという:
g ∘ f = 1_A かつ f ∘ g = 1_B。

この定義は圏論的な概念しか用いないため、Awodey は抽象的概念の一例として挙げている。

これを Scalaz にも広げて考えると、抽象的な型クラスの性質を習うことは、それがサポートする全ての具象的データ構造に適用できるという利点がある。

圏の例

抽象的に行く前に具象圏をいくつか紹介する。昨日は一つの圏の話しかしてこなかったので、これは役に立つことだと思う。

Sets

集合と全域関数の圏は太字で Sets と表記する。

Sets_fin

全ての有限集合とその間の全域関数を Sets_fin という。今まで見てきた圏がこれだ。

Pos

Awodey も和訳が見つからなかったので勝手訳になる:

数学でよく見るものに構造的集合 (structured set)、つまり集合に何らかの「構造」を追加したものと、それを「保存する」関数の圏というものがある。（構造と保存の定義は独自に与えられる）

半順序集合 (partially ordered set)、または略して poset と呼ばれる集合 A は、全ての a, b, c ∈ A に対して以下の条件が成り立つ二項関係 a ≤_A b を持つ:
反射律 (reflexivity): a ≤_A a
推移律 (transitivity): もし a ≤_A b かつ b ≤_A c ならば a ≤_A c
反対称律 (antisymmetry): もし a ≤_A b かつ b ≤_A a ならば a = b
poset A から poset B への射は単調 (monotone) な関数 m: A => B で、これは全ての a, a’ ∈ A に対して以下が成り立つという意味だ:
a ≤_A a’ のとき m(a) ≤_A m(a’)

関数が単調 (monotone) であるかぎり対象は圏の中にとどまるため、「構造」が保存されると言える。poset と単調関数の圏は Pos と表記される。Awodey は poset が好きなので、これを理解しておくのは重要。

Cat

定義 1.2. 函手 (functor)
F: C => D
は、圏 C と圏 D の間で以下の条件が成り立つように対象を対象に、また射を射に転写する:
F(f: A => B) = F(f): F(A) => F(B)
F(1_A) = 1_F(A)
F(g ∘ f) = F(g) ∘ F(f)
つまり、F はドメインとコドメイン、恒等射、および射の合成を保存する。

ついにきた。函手 (functor) は 2つの圏の間の射だ。以下が外部図式となる:

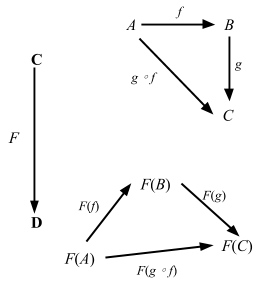
functor

F(A)、 F(B)、 F(C) の位置が歪んでいるのは意図的なものだ。F は上の図を少し歪ませているけども、射の合成関係は保存している。

この圏と函手の圏は Cat と表記される。

モノイド

モノイド (単位元を持つ半群とも呼ばれる) は、集合 M で、二項演算 ·: M × M => M と特定の「単位元」(unit) u ∈ M を持ち、任意の x, y, z ∈ M に対して以下の条件を満たすもの:
x · (y · z) = (x · y) · z
u · x = x = x · u
同義として、モノイドは唯一つの対象を持つ圏である。その圏の射はモノイドの要素だ。特に恒等射は単位元 u である。射の合成はモノイドの二項演算 m · n だ。

モノイドの概念は Scalaz にうまく翻訳できる。3日目のMonoid についてを見てほしい。

trait Monoid[A] extends Semigroup[A] { self =>
  ////
  /** The identity element for `append`. */
  def zero: A
  
  ...
}

trait Semigroup[A]  { self =>
  def append(a1: A, a2: => A): A
  ...
}

Int の加算と 0 はこうなる:

scala> 10 |+| Monoid[Int].zero
res26: Int = 10

Int の乗算と 1:

scala>  Tags.Multiplication(10) |+| Monoid[Int @@ Tags.Multiplication].zero
res27: scalaz.@@[Int,scalaz.Tags.Multiplication] = 10

このモノイドがただ一つの対象を持つ圏という考え方は「何を言っているんだ」と前は思ったものだけど、単集合を見ているので今なら理解できる気がする。

Mon

モノイドとモノイドの構造を保存した関数の圏は Mon と表記される。このような構造を保存する射は準同型写像 (homomorphism) と呼ばれる。

モノイド M からモノイド N への準同型写像は、関数 h: M => N で全ての m, n ∈ M について以下の条件を満たすも
h(m ·_M n) = h(m) ·_N h(n)
h(u_M) = u_N

それぞれのモノイドは圏なので、モノイド準同型写像は函手の特殊形だと言える。

Groups

定義 1.4 群 (group) G は、モノイドのうち全ての要素 g に対して逆射 g^-1 を持つもの。つまり、G は唯一つの対象を持つ圏で、全ての射が同型射となっている。

群と群の準同型写像の圏は Groups と表記される。

Scalaz に以前は群があったみたいだけど、一年ぐらい前に Spire とカブっているという理由で #279 にて削除された。

始対象と終対象

ちょっと抽象的なものを見ていこう。定義が圏論的な概念 (対象と射) のみに依存すると、よく「図式 abc が与えられたとき、別の図式 xyz が可換となる (commute) ような唯一の x が存在する」という形式になる。この場合の可換性とは、全ての射が正しく合成できるといった意味だ。このような定義は普遍性 (universal property) または普遍写像性 (universal mapping property) と呼ばれ、英語だと長いので UMP と略される。

集合論から来る概念もあるけども、抽象的な性質からより強力なものになっている。Sets の空集合と唯一つだけの要素を持つ集合を抽象化することを考えてみる。

定義 2.9 任意の圏 C において、
始対象 (initial) 0 は、任意の対象 C に対して以下を満たす一意の射を持つ
0 => C
終対象 (terminal) 1 は、任意の対象 C に対して以下を満たす一意の射を持つ
C => 1

同型を除いて一意

普遍写像性一般に言えることとして、一意と言った場合にこの要件は同型を除く (unique up to isomorphism) ということだ。考え方を変えると、もし対象 A と B が同型ならば「何らかの意味で等しい」ということでもある。これを記号化して A ≅ B と表記する。

命題 2.10 全ての始対象 (終対象) は同型を除いて一意である
証明。もし仮に C と C’ が両方とも同じ圏内の任意の始対象 (終対象) であるならば、そこには一意の同型射 C => C’ が存在する。0 と 0’ がある圏 C の始対象であるとする。以下の図式により、0 と 0’ が一意に同型であることは明らか:

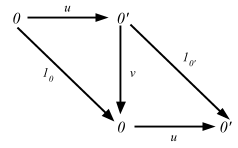
initial objects

同型射の定義は g ∘ f = 1_A かつ f ∘ g = 1_B なので、確かにこれで合ってる。

例

Sets 圏において、空集合は始対象であり、任意の単集合 {x} は終対象だ。

どうやら空関数という概念があって、空集合から任意の集合へ関数が出ているらしい。

poset では、対象は最小の要素を持つとき始対象で、最大の要素を持つ場合に終対象となる。

poset では ≤ の構造を保存しなければいけないので、何となく分かる気がする。

他にも多くの例があるけども、面白いのは一見すると無関係な概念が同じ構造を持っているということだ。

積

まずは集合の積を考える。集合 A と B があるとき、A と B のデカルト積は順序対 (ordered pairs) の集合となる
A × B = {(a, b)| a ∈ A, b ∈ B}

2つの座標射影 (coordinate projection) があって
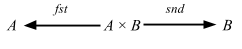
coordinate projections

これは以下の条件を満たす:

fst ∘ (a, b) = a
snd ∘ (a, b) = b

この積という考えは case class やタプルの基底 trait である scala.Product にも関連する。

任意の要素 c ∈ A × B に対して、c = (fst ∘ c, snd ∘ c) ということができる。

昨日と同じトリックを使って、明示的に単集合を導入する:

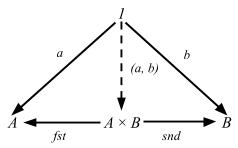
product of sets

この(外部)図式は上の条件を捕捉している。ここで 1-要素を一般化すると圏論的定義が得られる。

定義 2.15. 任意の圏 C において、対象 A と B の積の図式は対象 P と射 p₁ と p₂ から構成され

以下の UMP を満たす:
この形となる任意の図式があるとき

次の図式

が可換となる (つまり、x₁ = p₁ u かつ x₂ = p₂ u が成立する) 一意の射 u: X => P が存在する。

この定義は普遍であるため、任意の圏に適用することができる。

積の一意性

普遍性は A と B の積の全てが同型を除いて一意であることも示唆する。

命題 2.17 積は同型を除いて一意である。

P と Q が対象 A と B の積であるとする。

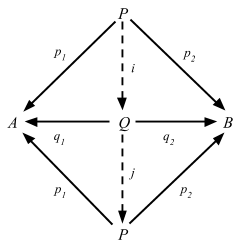
uniqueness of products

P は積であるため、p₁ = q₁ ∘ i かつ p₂ = q₂ ∘ i を満たす一意の i: P => Q が存在する。
Q は積であるため、q₁ = p₁ ∘ j かつ q₂ = p₂ ∘ j を満たす一意の j: Q => P が存在する。
i と j を合成することで 1_P = j ∘ i が得られる。
同様にして 1_Q = i ∘ j。
i は同型射、P ≅ Q である。∎

全ての積は同型であるため、一つを取って A × B と表記する。また、射 u: X => A × B は ⟨x₁, x₂⟩ と表記する。

例

Sets 圏ではデカルト積が積となることは紹介した。

P が poset だとして、要素 p, q ∈ P の積を考える。以下のような射影が必要なる
p × q ≤ p
p × q ≤ q
　そして任意の要素 x で x ≤ p かつ x ≤ q であるものに対しては
x ≤ p × q
を満たす必要がある。

この場合 p × q は最大下限 (greatest lower bound) となる。

双対性

逆圏

双対性に入る前に、既存の圏から別の圏を生成するということを話しておく必要がある。ここで注意してほしいのは、今まで取り扱ってきた対象ではなくて圏の話をしているということで、これは対象と射の両方を含む。

任意の圏 C の逆圏 (opposite category、また dual「双対圏」とも) C^op は、C と同じ対象を持つが、C^op 内の射は C では f: D => C である。つまり、C^op は C の射を形式的に逆向きにしたものだ。

双対性原理

この考えをさらに進めて、圏論内の任意の文 Σ の以下を置換して「双対文」Σ^* を得ることができる。

f ∘ g の代わりに g ∘ f
コドメインの代わりにドメイン
ドメインの代わりにコドメイン

意味論的にどれが f で g なのかに重要性は無いため、Σ が圏論のみに基づいているかぎり双対文も成り立つ。そのため、ある概念についての任意の証明はその双対に対しても成り立つ。これは双対性原理 (duality principle) と呼ばれる。

別の見方をすると、もし Σ が全ての圏 C について成り立つとした場合、C^op でも成り立つことになる。そのため、Σ^* は (C^op)^op、つまり C でも成り立つことになる。

始対象と終対象の定義をもう一度見てみよう:

定義 2.9 任意の圏 C において、
始対象 (initial) 0 は、任意の対象 C に対して以下を満たす一意の射を持つ
0 => C
終対象 (terminal) 1 は、任意の対象 C に対して以下を満たす一意の射を持つ
C => 1

これはお互いの双対となっているため、圏 C での始対象は逆圏 C^op での終対象となる。

ここで「全ての始対象は同型を除いて一意である」という命題の定義を思い出してほしい。
initial objects

上の図式内の全ての射の方向を逆転すると、終対象に関する証明が得られる。
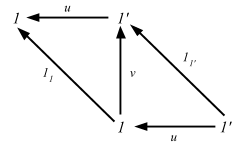
initial objects

これは結構すごい。続きはまた今度。

21日目

20日目は引き続き圏論の基礎概念を見てきた。抽象的に考えることを強調したAwodey にガイドを切り替えた。特に、僕が目指してしたのは双対性という概念で、これによって圏論の抽象概念は射の方向をひっくり返しても成り立つことが分かった。

余積

双対としてよく知られているものに、積の双対である余積 (coproduct、「直和」とも) がある。双対を表すのに英語では頭に “co-” を、日本語だと「余」を付ける。

以下に積の定義を再掲する:

定義 2.15. 任意の圏 C において、対象 A と B の積の図式は対象 P と射 p₁ と p₂ から構成され

以下の UMP を満たす:
この形となる任意の図式があるとき

次の図式

が可換となる (つまり、x₁ = p₁ u かつ x₂ = p₂ u が成立する) 一意の射 u: X => P が存在する。

矢印をひっくり返すと余積図式が得られる:
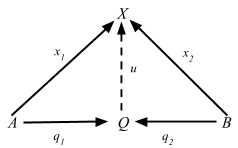
coproducts

余積は同型を除いて一意なので、余積は A + B、u: A + B => X の射は [f, g] と表記することができる。

「余射影」の i₁: A => A + B と i₂: B => A + B は、単射 (“injective”) ではなくても「単射」 (“injection”) という。

「埋め込み」(embedding) ともいうみたいだ。積が scala.Product などでエンコードされる直積型に関係したように、余積は直和型 (sum type, union type) と関連する:

data TrafficLight = Red | Yellow | Green

Unboxed union types

case class や sealed trait を使って直和型をエンコードすると、例えば Int と String の union を作ろうとしたときにうまくいかない。これに関して面白いのが Miles Sabin (@milessabin) さんの Unboxed union types in Scala via the Curry-Howard isomorphismだ。

誰もがド・モルガンの法則は見たことがあると思う:
!(A || B) <=> (!A && !B)

Scala には A with B 経由で論理積があるため、Miles は否定さえエンコードできれば論理和を得られることを発見した。これは Scalaz では scalaz.UnionTypes として移植された:

trait UnionTypes {
  type ![A] = A => Nothing
  type !![A] = ![![A]]

  trait Disj { self =>
    type D
    type t[S] = Disj {
      type D = self.D with ![S]
    }
  }

  type t[T] = {
    type t[S] = (Disj { type D = ![T] })#t[S]
  }

  type or[T <: Disj] = ![T#D]

  type Contains[S, T <: Disj] = !![S] <:< or[T]
  type ∈[S, T <: Disj] = Contains[S, T]

  sealed trait Union[T] {
    val value: Any
  }
}

object UnionTypes extends UnionTypes

Miles の size の例を実装してみる:

scala> import UnionTypes._
import UnionTypes._

scala> type StringOrInt = t[String]#t[Int]
defined type alias StringOrInt

scala> implicitly[Int ∈ StringOrInt]
res0: scalaz.UnionTypes.∈[Int,StringOrInt] = <function1>

scala> implicitly[Byte ∈ StringOrInt]
<console>:18: error: Cannot prove that Byte <:< StringOrInt.
              implicitly[Byte ∈ StringOrInt]
                        ^

scala> def size[A](a: A)(implicit ev: A ∈ StringOrInt): Int = a match {
         case i: Int    => i
         case s: String => s.length  
       }
size: [A](a: A)(implicit ev: scalaz.UnionTypes.∈[A,StringOrInt])Int

scala> size(23)
res2: Int = 23

scala> size("foo")
res3: Int = 3

\/

Scalaz にある \/ も、直和型の一種だと考えることができる。シンボルを使った名前である \/ も、∨ が論理和 (logical disjunction) を表すことを考えると納得がいく。これは7日目でカバーした。 size の例を書き換えるとこうなる:

scala> def size(a: String \/ Int): Int = a match {
         case \/-(i) => i
         case -\/(s) => s.length  
       }
size: (a: scalaz.\/[String,Int])Int

scala> size(23.right[String])
res15: Int = 23

scala> size("foo".left[Int])
res16: Int = 3

Coproduct と Inject

Scalaz には実は Coproduct もあって、これは型コンストラクタのための Either のようなものだ:

final case class Coproduct[F[_], G[_], A](run: F[A] \/ G[A]) {
  ...
}

object Coproduct extends CoproductInstances with CoproductFunctions

trait CoproductFunctions {
  def leftc[F[_], G[_], A](x: F[A]): Coproduct[F, G, A] =
    Coproduct(-\/(x))

  def rightc[F[_], G[_], A](x: G[A]): Coproduct[F, G, A] =
    Coproduct(\/-(x))

  ...
}

Data types à la carte で、Wouter Swierstra (@wouterswierstra) さんがこれを使っていわゆる Expression Problem と呼ばれているものを解決できると解説している:

目標は、既にあるコードを再コンパイルしたり型安全性を失うこと無く、ケースごとにデータ型を定義して、データ型に新たなケースを追加したり、データ型を受け取る新たな関数を定義できるようにすることだ。

この論文で述べられている automatic injection は、@ethul によって #502 で Scalaz にコントリビュートされた。具体例は typeclass-inject の README を参照してほしい。

それぞれの式は Free[F, Int] を構築していて、F は 3つの代数系の余積となっている。

Hom 集合

飛ばした概念もあるので、少し前に戻る。

大きい圏、小さい圏、局所的に小さい圏

定義 1.11. 任意の圏 C において、C の対象の集まり C₀ と、C の射の集まり C₁ が集合であるとき、小さい圏という。その他の場合は、C は大きいという。
例えば、全ての有限圏は明らかに小さいが、有限集合と関数の圏である Sets_fin も小さい。

Cat は、実は全ての小さい圏の圏であるため、Cat は自身を含まない。

定義 1.12. 任意の圏 C は、C の全ての対象 X と Y について、Hom_C(X, Y) = { f ∈ C₁ | f: X = Y } という集まりが集合であるとき、局所的に小さいといい、これを hom集合という。

Hom集合

Hom集合 (Hom-set) は Hom(A, B) と表記され、対象 A と B の射の集合だ。Hom集合は対象を射だけを使って検査 (要素を見ること) することができるため、役に立つ。

C の任意の射 f: A => B を Hom(X, A) に入れると関数が得られる:

Hom(X, f): Hom(X, A) => Hom(X, B)
case x => (f ∘ x: X => A => B)

つまり、Hom(X, f) = f ∘ _ となる。

Sets 圏で単集合のトリックを使うことで、A ≅ Hom_Sets(1, A) であることを利用できる。これを一般化すると、Hom(X, A) は、X から見た generalized element の集合だと考えることができる。
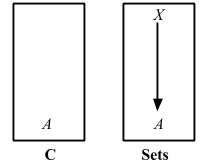
generalized elements

A を _ で置換することで函手を作ることができる
> Hom(X, _): C => Sets.
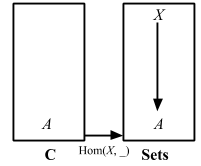
representable functor

この函手は representable functor または共変Hom函手と呼ばれる。

Hom集合で考える

任意の対象 P について、射のペア p₁: P => A と p₂: P => B によって集合
Hom(P, A) × Hom(P, B)
の要素 (p₁, p₂) を決定することができる。

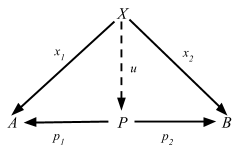
product of objects

上の図式によって、x: X => P が与えられれば、それを p₁ と p₂ に合成することによって、それぞれ x₁ と x₂ が得られることが分かる。射の合成は Hom集合では関数であるため、これも関数として書くことができる:

ϑ_X = (Hom(X, p₁), Hom(X, p₂)): Hom(X, P) => Hom(X, A) × Hom(X, B)
ただし ϑ_X(x) = (x₁, x₂)

命題 2.20. 以下の形式の図式

は、全ての対象 X に関して、(2.1) で与えられるカノニカル関数 ϑ_X が同型
ϑ_X: Hom(X, P) ≅ Hom(P, A) × Hom(P, B)
であり、その時に限り、A と B の積である。

これは図式を同型等式で入れ替えることができたという意味で興味深い。

Natural Transformation

そろそろ自然性にチャレンジできるぐらい経験値を積んだだろうか。本の中程 7.4節まで飛ばしてみよう。

自然変換 (natural transformation) は函手の射だ。その通り。与えられた圏 C と D について、函手 C => D を新たな圏の「対象」として考えて、これらの対象間の射を自然変換と呼ぶことにする。

Scala での自然変換に関していくつか面白い記事が書かれている:

Higher-Rank Polymorphism in Scala, Rúnar (@runarorama) July 2, 2010
Type-Level Programming in Scala, Part 7: Natural transformation literals, Mark Harrah (@harrah) October 26, 2010
First-class polymorphic function values in shapeless (2 of 3) — Natural Transformations in Scala, Miles Sabin (@milessabin) May 10, 2012

Mark さんがシンプルな具体例を挙げて自然変換が何故必要なのかを説明している:

自然変換に進むと問題に直面する。例えば、全ての T に関して Option[T] を List[T] へと投射する関数は定義することはできない。これが自明でなければ、以下がコンパイルするような toList を定義してみよう:

val toList = ...
 
val a: List[Int] = toList(Some(3))
assert(List(3) == a)
 
val b: List[Boolean] = toList(Some(true))
assert(List(true) == b)

自然変換 M ~> N (ここでは M=Option、N=List) を定義するには、暗黙のクラスを作る必要がある。Scala には量化された関数 (quantified function) を定義するリテラルが無いからだ。

これは Scalaz に移植されている。NaturalTransformation をみてみよう:

/** A universally quantified function, usually written as `F ~> G`,
  * for symmetry with `A => B`.
  * ....
  */
trait NaturalTransformation[-F[_], +G[_]] {
  self =>
  def apply[A](fa: F[A]): G[A]

  ....
}

シンボルを使ったエイリアスは scalaz 名前空間の package object 内にて定義されている:

  /** A [[scalaz.NaturalTransformation]][F, G]. */
  type ~>[-F[_], +G[_]] = NaturalTransformation[F, G]
  /** A [[scalaz.NaturalTransformation]][G, F]. */
  type <~[+F[_], -G[_]] = NaturalTransformation[G, F]

toList を定義してみる:

scala> val toList = new (Option ~> List) {
         def apply[T](opt: Option[T]): List[T] =
           opt.toList
       }
toList: scalaz.~>[Option,List] = 1@2fdb237

scala> toList(3.some)
res17: List[Int] = List(3)

scala> toList(true.some)
res18: List[Boolean] = List(true)

これを圏論の用語を比較してみると、Scalaz の世界では List や Option のような型コンストラクタは 2つの圏を map する Functor をサポートしている。

trait Functor[F[_]] extends InvariantFunctor[F] { self =>
  ////

  /** Lift `f` into `F` and apply to `F[A]`. */
  def map[A, B](fa: F[A])(f: A => B): F[B]
  ...
}

これは、より一般的な C => D に比べてかなり限定的な函手だと言えるが、型コンストラクタを圏と考えれば確かに函手ではある。
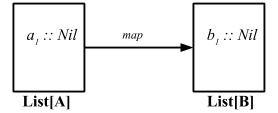
functors in Scala

NaturalTransformation (~>) が型コンストラクタ (一次カインド型) のレベルではたらくため、それは函手間の射 (または圏の間の射のファミリー) だと言える。
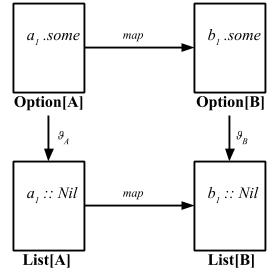
nats in Scala

続きはまたここから。

読んでくれてありがとう

このページは終わりのための仮ページだけども気が向いたらまた更新するかもしれない。コメントや retweet ありがとう!

Learn You a Haskell for Great Good! を書いた Miran Lipovača さんにまず賞賛の言葉を送りたい。邦訳はすごいHaskellたのしく学ぼう!。例題がたくさんあるこの本がガイド役だったことが本当に助かった。

そして Scalaz の作者やコントリビュータの皆にも賛辞が必要だ! リストのトップ10の方 (敬称略):

@retronym Jason Zaugg
@xuwei-k Kenji Yoshida
@tonymorris Tony Morris
@larsrh Lars Hupel
@runarorama Rúnar
@S11001001 Stephen Compall
@purefn Richard Wallace
@nuttycom Kris Nuttycombe
@ekmett Edward Kmett
@pchiusano Paul Chiusano

Scalaz を通した関数型プログラミングを習ったのは楽しかったし、今後も独習を続けていきたい。あと、それから Scalaz cheat sheet もよろしく。

Scalaz cheatsheet

Equal[A]

def equal(a1: A, a2: A): Boolean
(1 === 2) assert_=== false
(2 =/= 1) assert_=== true

Order[A]

def order(x: A, y: A): Ordering
1.0 ?|? 2.0 assert_=== Ordering.LT
1.0 lt 2.0 assert_=== true
1.0 gt 2.0 assert_=== false
1.0 lte 2.0 assert_=== true
1.0 gte 2.0 assert_=== false
1.0 max 2.0 assert_=== 2.0
1.0 min 2.0 assert_=== 1.0

Show[A]

def show(f: A): Cord
1.0.show assert_=== Cord("1.0")
1.0.shows assert_=== "1.0"
1.0.print assert_=== ()
1.0.println assert_=== ()

Enum[A] extends Order[A]

def pred(a: A): A
def succ(a: A): A
1.0 |-> 2.0 assert_=== List(1.0, 2.0)
1.0 |--> (2, 5) assert_=== List(1.0, 3.0, 5.0)
// |=>/|==>/from/fromStep return EphemeralStream[A]
(1.0 |=> 2.0).toList assert_=== List(1.0, 2.0)
(1.0 |==> (2, 5)).toList assert_=== List(1.0, 3.0, 5.0)
(1.0.from take 2).toList assert_=== List(1.0, 2.0)
((1.0 fromStep 2) take 2).toList assert_=== List(1.0, 3.0)
1.0.pred assert_=== 0.0
1.0.predx assert_=== Some(0.0)
1.0.succ assert_=== 2.0
1.0.succx assert_=== Some(2.0)
1.0 -+- 1 assert_=== 2.0
1.0 --- 1 assert_=== 0.0
Enum[Int].min assert_=== Some(-2147483648)
Enum[Int].max assert_=== Some(2147483647)

Semigroup[A]

def append(a1: A, a2: => A): A
List(1, 2) |+| List(3) assert_=== List(1, 2, 3)
List(1, 2) mappend List(3) assert_=== List(1, 2, 3)
1 |+| 2 assert_=== 3
(Tags.Multiplication(2) |+| Tags.Multiplication(3): Int) assert_=== 6
// Tags.Disjunction (||), Tags.Conjunction (&&)
(Tags.Disjunction(true) |+| Tags.Disjunction(false): Boolean) assert_=== true
(Tags.Conjunction(true) |+| Tags.Conjunction(false): Boolean) assert_=== false
(Ordering.LT: Ordering) |+| (Ordering.GT: Ordering) assert_=== Ordering.LT
(none: Option[String]) |+| "andy".some assert_=== "andy".some
(Tags.First('a'.some) |+| Tags.First('b'.some): Option[Char]) assert_=== 'a'.some
(Tags.Last('a'.some) |+| Tags.Last(none: Option[Char]): Option[Char]) assert_=== 'a'.some

Monoid[A] extends Semigroup[A]

def zero: A
mzero[List[Int]] assert_=== Nil

Functor[F[_]]

def map[A, B](fa: F[A])(f: A => B): F[B]
List(1, 2, 3) map {_ + 1} assert_=== List(2, 3, 4)
List(1, 2, 3) ∘ {_ + 1} assert_=== List(2, 3, 4)
List(1, 2, 3) >| "x" assert_=== List("x", "x", "x")
List(1, 2, 3) as "x" assert_=== List("x", "x", "x")
List(1, 2, 3).fpair assert_=== List((1,1), (2,2), (3,3))
List(1, 2, 3).strengthL("x") assert_=== List(("x",1), ("x",2), ("x",3))
List(1, 2, 3).strengthR("x") assert_=== List((1,"x"), (2,"x"), (3,"x"))
List(1, 2, 3).void assert_=== List((), (), ())
Functor[List].lift {(_: Int) * 2} (List(1, 2, 3)) assert_=== List(2, 4, 6)

Apply[F[_]] extends Functor[F]

def ap[A,B](fa: => F[A])(f: => F[A => B]): F[B]
1.some <*> {(_: Int) + 2}.some assert_=== Some(3) // except in 7.0.0-M3
1.some <*> { 2.some <*> {(_: Int) + (_: Int)}.curried.some } assert_=== 3.some
1.some <* 2.some assert_=== 1.some
1.some *> 2.some assert_=== 2.some
Apply[Option].ap(9.some) {{(_: Int) + 3}.some} assert_=== 12.some
Apply[List].lift2 {(_: Int) * (_: Int)} (List(1, 2), List(3, 4)) assert_=== List(3, 4, 6, 8)
(3.some |@| 5.some) {_ + _} assert_=== 8.some
// ^(3.some, 5.some) {_ + _} assert_=== 8.some

Applicative[F[_]] extends Apply[F]

def point[A](a: => A): F[A]
1.point[List] assert_=== List(1)
1.η[List] assert_=== List(1)

Product/Composition

(Applicative[Option] product Applicative[List]).point(0) assert_=== (0.some, List(0))
(Applicative[Option] compose Applicative[List]).point(0) assert_=== List(0).some

Bind[F[_]] extends Apply[F]

def bind[A, B](fa: F[A])(f: A => F[B]): F[B]
3.some flatMap { x => (x + 1).some } assert_=== 4.some
(3.some >>= { x => (x + 1).some }) assert_=== 4.some 
3.some >> 4.some assert_=== 4.some
List(List(1, 2), List(3, 4)).join assert_=== List(1, 2, 3, 4)

Monad[F[_]] extends Applicative[F] with Bind[F]

// no contract function
// failed pattern matching produces None
(for {(x :: xs) <- "".toList.some} yield x) assert_=== none
(for { n <- List(1, 2); ch <- List('a', 'b') } yield (n, ch)) assert_=== List((1, 'a'), (1, 'b'), (2, 'a'), (2, 'b'))
(for { a <- (_: Int) * 2; b <- (_: Int) + 10 } yield a + b)(3) assert_=== 19
List(1, 2) filterM { x => List(true, false) } assert_=== List(List(1, 2), List(1), List(2), List())

Plus[F[_]]

def plus[A](a: F[A], b: => F[A]): F[A]
List(1, 2) <+> List(3, 4) assert_=== List(1, 2, 3, 4)

PlusEmpty[F[_]] extends Plus[F]

def empty[A]: F[A]
(PlusEmpty[List].empty: List[Int]) assert_=== Nil

ApplicativePlus[F[_]] extends Applicative[F] with PlusEmpty[F]

// no contract function

MonadPlus[F[_]] extends Monad[F] with ApplicativePlus[F]

// no contract function
List(1, 2, 3) filter {_ > 2} assert_=== List(3)

Foldable[F[_]]

def foldMap[A,B](fa: F[A])(f: A => B)(implicit F: Monoid[B]): B
def foldRight[A, B](fa: F[A], z: => B)(f: (A, => B) => B): B
List(1, 2, 3).foldRight (0) {_ + _} assert_=== 6
List(1, 2, 3).foldLeft (0) {_ + _} assert_=== 6
(List(1, 2, 3) foldMap {Tags.Multiplication}: Int) assert_=== 6
List(1, 2, 3).foldLeftM(0) { (acc, x) => (acc + x).some } assert_=== 6.some

Traverse[F[_]] extends Functor[F] with Foldable[F]

def traverseImpl[G[_]:Applicative,A,B](fa: F[A])(f: A => G[B]): G[F[B]]
List(1, 2, 3) traverse { x => (x > 0) option (x + 1) } assert_=== List(2, 3, 4).some
List(1, 2, 3) traverseU {_ + 1} assert_=== 9
List(1.some, 2.some).sequence assert_=== List(1, 2).some
1.success[String].leaf.sequenceU map {_.drawTree} assert_=== "1\n".success[String]

Length[F[_]]

def length[A](fa: F[A]): Int
List(1, 2, 3).length assert_=== 3

Index[F[_]]

def index[A](fa: F[A], i: Int): Option[A]
List(1, 2, 3) index 2 assert_=== 3.some
List(1, 2, 3) index 3 assert_=== none

ArrId[=>:[, ]]

def id[A]: A =>: A

Compose[=>:[, ]]

def compose[A, B, C](f: B =>: C, g: A =>: B): (A =>: C)
val f1 = (_:Int) + 1
val f2 = (_:Int) * 100
(f1 >>> f2)(2) assert_=== 300
(f1 <<< f2)(2) assert_=== 201

Category[=>:[, ]] extends ArrId[=>:] with Compose[=>:]

// no contract function

Arrow[=>:[, ]] extends Category[=>:]

def arr[A, B](f: A => B): A =>: B
def first[A, B, C](f: (A =>: B)): ((A, C) =>: (B, C))
val f1 = (_:Int) + 1
val f2 = (_:Int) * 100
(f1 *** f2)(1, 2) assert_=== (2, 200)
(f1 &&& f2)(1) assert_=== (2,100)

Unapply[TC[`_`[`_`]], MA]

type M[_]
type A
def TC: TC[M]
def apply(ma: MA): M[A]
implicitly[Unapply[Applicative, Int => Int]].TC.point(0).asInstanceOf[Int => Int](10) assert_=== Applicative[({type l[x]=Function1[Int, x]})#l].point(0)(10)
List(1, 2, 3) traverseU {(x: Int) => {(_:Int) + x}} apply 1 assert_=== List(2, 3, 4) // traverse won't work

Boolean

false /\ true assert_=== false // &&
false \/ true assert_=== true // ||
(1 < 10) option 1 assert_=== 1.some
(1 > 10)? 1 | 2 assert_=== 2
(1 > 10)?? {List(1)} assert_=== Nil

Option

1.some assert_=== Some(1)
none[Int] assert_=== (None: Option[Int])
1.some? 'x' | 'y' assert_=== 'x'
1.some | 2 assert_=== 1 // getOrElse

Id[+A] = A

// no contract function
1 + 2 + 3 |> {_ * 6}
1 visit { case x@(2|3) => List(x * 2) }

Tagged[A]

sealed trait KiloGram
def KiloGram[A](a: A): A @@ KiloGram = Tag[A, KiloGram](a)
def f[A](mass: A @@ KiloGram): A @@ KiloGram

Tree[A]/TreeLoc[A]

val tree = 'A'.node('B'.leaf, 'C'.node('D'.leaf), 'E'.leaf)
(tree.loc.getChild(2) >>= {_.getChild(1)} >>= {_.getLabel.some}) assert_=== 'D'.some
(tree.loc.getChild(2) map {_.modifyLabel({_ => 'Z'})}).get.toTree.drawTree assert_=== 'A'.node('B'.leaf, 'Z'.node('D'.leaf), 'E'.leaf).drawTree

Stream[A]/Zipper[A]

(Stream(1, 2, 3, 4).toZipper >>= {_.next} >>= {_.focus.some}) assert_=== 2.some
(Stream(1, 2, 3, 4).zipperEnd >>= {_.previous} >>= {_.focus.some}) assert_=== 3.some
(for { z <- Stream(1, 2, 3, 4).toZipper; n1 <- z.next } yield { n1.modify {_ => 7} }) map { _.toStream.toList } getOrElse Nil assert_=== List(1, 7, 3, 4)
unfold(3) { x => (x =/= 0) option (x, x - 1) }.toList assert_=== List(3, 2, 1)

DList[A]

DList.unfoldr(3, { (x: Int) => (x =/= 0) option (x, x - 1) }).toList assert_=== List(3, 2, 1)

Lens[A, B] = LensT[Id, A, B]

val t0 = Turtle(Point(0.0, 0.0), 0.0)
val t1 = Turtle(Point(1.0, 0.0), 0.0)
val turtlePosition = Lens.lensu[Turtle, Point] (
  (a, value) => a.copy(position = value),
  _.position)
val pointX = Lens.lensu[Point, Double] (
  (a, value) => a.copy(x = value),
  _.x)
val turtleX = turtlePosition >=> pointX
turtleX.get(t0) assert_=== 0.0
turtleX.set(t0, 5.0) assert_=== Turtle(Point(5.0, 0.0), 0.0)
turtleX.mod(_ + 1.0, t0) assert_=== t1
t0 |> (turtleX =>= {_ + 1.0}) assert_=== t1
(for { x <- turtleX %= {_ + 1.0} } yield x) exec t0 assert_=== t1
(for { x <- turtleX := 5.0 } yield x) exec t0 assert_=== Turtle(Point(5.0, 0.0), 0.0)
(for { x <- turtleX += 1.0 } yield x) exec t0 assert_=== t1

Validation[+E, +A]

(1.success[String] |@| "boom".failure[Int] |@| "boom".failure[Int]) {_ |+| _ |+| _} assert_=== "boomboom".failure[Int]
(1.successNel[String] |@| "boom".failureNel[Int] |@| "boom".failureNel[Int]) {_ |+| _ |+| _} assert_=== NonEmptyList("boom", "boom").failure[Int]
"1".parseInt.toOption assert_=== 1.some

Writer[+W, +A] = WriterT[Id, W, A]

(for { x <- 1.set("log1"); _ <- "log2".tell } yield (x)).run assert_=== ("log1log2", 1)
import std.vector._
MonadWriter[Writer, Vector[String]].point(1).run assert_=== (Vector(), 1)

\/[+A, +B]

1.right[String].isRight assert_=== true
1.right[String].isLeft assert_=== false
1.right[String] | 0 assert_=== 1  // getOrElse
("boom".left ||| 2.right) assert_=== 2.right // orElse
("boom".left[Int] >>= { x => (x + 1).right }) assert_=== "boom".left[Int]
(for { e1 <- 1.right; e2 <- "boom".left[Int] } yield (e1 |+| e2)) assert_=== "boom".left[Int]

Kleisli[M[+_], -A, +B]

val k1 = Kleisli { (x: Int) => (x + 1).some }
val k2 = Kleisli { (x: Int) => (x * 100).some }
(4.some >>= k1 compose k2) assert_=== 401.some
(4.some >>= k1 <=< k2) assert_=== 401.some
(4.some >>= k1 andThen k2) assert_=== 500.some
(4.some >>= k1 >=> k2) assert_=== 500.some

Reader[E, A] = Kleisli[Id, E, A]

Reader { (_: Int) + 1 }

trait Memo[K, V]

val memoizedFib: Int => Int = Memo.mutableHashMapMemo {
  case 0 => 0
  case 1 => 1
  case n => memoizedFib(n - 2) + memoizedFib(n - 1)
}

State[S, +A] = StateT[Id, S, A]

State[List[Int], Int] { case x :: xs => (xs, x) }.run(1 :: Nil) assert_=== (Nil, 1)
(for {
  xs <- get[List[Int]]
  _ <- put(xs.tail)
} yield xs.head).run(1 :: Nil) assert_=== (Nil, 1)

ST[S, A]/STRef[S, A]/STArray[S, A]

import scalaz._, Scalaz._, effect._, ST._
type ForallST[A] = Forall[({type l[x] = ST[x, A]})#l]
def e1[S]: ST[S, Int] = for {
  x <- newVar[S](0)
  _ <- x mod {_ + 1}
  r <- x.read
} yield r
runST(new ForallST[Int] { def apply[S] = e1[S] }) assert_=== 1
def e2[S]: ST[S, ImmutableArray[Boolean]] = for {
  arr <- newArr[S, Boolean](3, true)
  x <- arr.read(0)
  _ <- arr.write(0, !x)
  r <- arr.freeze
} yield r
runST(new ForallST[ImmutableArray[Boolean]] { def apply[S] = e2[S] })(0) assert_=== false

IO[+A]

import scalaz._, Scalaz._, effect._, IO._
val action1 = for {
  x <- readLn
  _ <- putStrLn("Hello, " + x + "!")
} yield ()
action1.unsafePerformIO

IterateeT[E, F[`_`], A]/EnumeratorT[O, I, F[`_`]]

import scalaz._, Scalaz._, iteratee._, Iteratee._
(length[Int, Id] &= enumerate(Stream(1, 2, 3))).run assert_=== 3
(length[scalaz.effect.IoExceptionOr[Char], IO] &= enumReader[IO](new BufferedReader(new FileReader("./README.md")))).run.unsafePerformIO

Free[S[+`_`], +A]

import scalaz._, Scalaz._, Free._
type FreeMonoid[A] = Free[({type λ[+α] = (A,α)})#λ, Unit]
def cons[A](a: A): FreeMonoid[A] = Suspend[({type λ[+α] = (A,α)})#λ, Unit]((a, Return[({type λ[+α] = (A,α)})#λ, Unit](())))
def toList[A](list: FreeMonoid[A]): List[A] =
  list.resume.fold(
    { case (x: A, xs: FreeMonoid[A]) => x :: toList(xs) },
    { _ => Nil })
toList(cons(1) >>= {_ => cons(2)}) assert_=== List(1, 2)

Trampoline[+A] = Free[Function0, A]

import scalaz._, Scalaz._, Free._
def even[A](ns: List[A]): Trampoline[Boolean] =
  ns match {
    case Nil => return_(true)
    case x :: xs => suspend(odd(xs))
  }
def odd[A](ns: List[A]): Trampoline[Boolean] =
  ns match {
    case Nil => return_(false)
    case x :: xs => suspend(even(xs))
  }
even(0 |-> 3000).run assert_=== false

Imports

import scalaz._ // imports type names
import scalaz.Id.Id // imports Id type alias
import scalaz.std.option._ // imports instances, converters, and functions related to `Option`
import scalaz.std.AllInstances._ // imports instances and converters related to standard types
import scalaz.std.AllFunctions._ // imports functions related to standard types
import scalaz.syntax.monad._ // injects operators to Monad
import scalaz.syntax.all._ // injects operators to all typeclasses and Scalaz data types
import scalaz.syntax.std.boolean._ // injects operators to Boolean
import scalaz.syntax.std.all._ // injects operators to all standard types
import scalaz._, Scalaz._ // all the above

Note

type Function1Int[A] = ({type l[x]=Function1[Int, x]})#l[A]
type Function1Int[A] = Function1[Int, A]

Contents

独習 Scalaz

リンク

0日目

Scalaz 入門

多相性って何?

パラメータ多相

派生型多態

アドホック多相

sum 関数

Monoid

FoldLeft

Scalaz の型クラス

メソッド注入 (enrich my library)

標準型構文

1日目

型クラス初級講座

sbt

Equal

Order

Show

Read

Enum

Bounded

Num

型クラス中級講座

信号の型クラス

Yes と No の型クラス

2日目

Functor

Functor としての関数

Applicative

Apply

Apply としての Option

Applicative Style

Apply としての List

Zip List

Applicative の便利な関数

3日目

型を司るもの、カインド

Tagged type

Monoid について

Monoid

Semigroup

Monoid に戻る

Tags.Multiplication

Tags.Disjunction and Tags.Conjunction

Monoid としての Ordering

4日目

Functor則

法則を破る

Applicative則

Semigroup則

Monoid則

Monoid としての Option

Foldable

5日目

モナドがいっぱい

Bind

Monad

綱渡り

ロープの上のバナナ

for 構文

帰ってきたピエール

パターンマッチングと失敗

List モナド

MonadPlus と guard 関数

Plus、PlusEmpty、と ApplicativePlus

MonadPlus 再び

騎士の旅

Monad則

左単位元

右単位元

結合律

6日目

for 構文、再び

Writer? 中の人なんていません!

Writer

WriterT

Writer に for 構文を使う