Determination and choice 

CM:

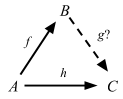
1. The ‘determination’ (or ‘extension’) problem
Given f and h as shown, what are all g, if any, for which h = g ∘ f?

2. The ‘choice’ (or ‘lifting’) problem
Given g and h as shown, what are all g, if any, for which h = g ∘ f?

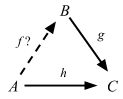
These two notions are analogous to division problem.

Retractions and sections 

Definitions: If f: A => B:

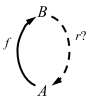
• a retraction for f is an arrow r: B => A for which r ∘ f = 1_A
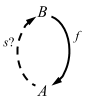
• a section for f is an arrow s: B => A for which f ∘ s = 1_B

Here’s the external diagram for retraction problem:

and one for section problem:

Surjective 

If an arrow f: A => B satisfies the property ‘for any y: T => B there exists an x: T => A such that f ∘ x = y‘, it is often said to be ‘surjective for arrows from T.’

I came up with my own example to think about what surjective means in set theory: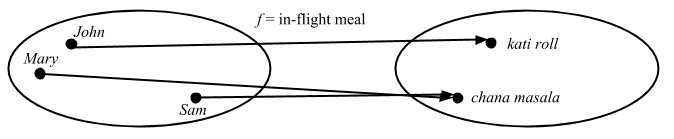

Suppose John and friends are on their way to India, and they are given two choices for their lunch in the flight: chicken wrap or spicy chick peas. Surjective means that given a meal, you can find at least one person who chose the meal. In other words, all elements in codomain are covered.

Now recall that we can generalize the concept of elements by introducing singleton explicitly.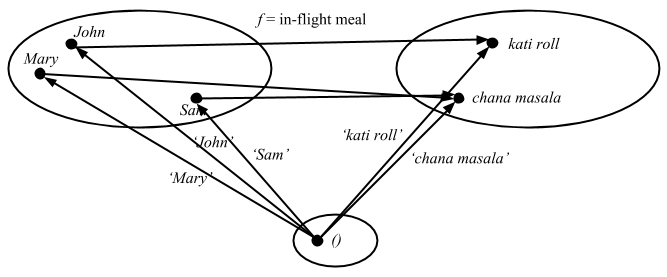

Compare this to the category theory’s definition of surjective: for any y: T => B there exists an x: T => A such that f ∘ x = y. For any arrow going from 1 to B (lunch), there is an arrow going from 1 to A (person) such that f ∘ x = y. In other words, f is surjective for arrows from 1.

Let’s look at this using an external diagram.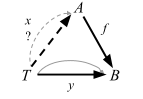

This is essentially the same diagram as the choice problem.

Injective and monomorphism 

Definitions: An arrow f satisfying the property ‘for any pair of arrows x₁: T => A and x₂: T => A, if f ∘ x₁ = f ∘ x₂ then x₁ = x₂‘, it is said to be injective for arrows from T.

If f is injective for arrows from T for every T, one says that f is injective, or is a monomorphism.

Here’s how injective would mean in terms of sets: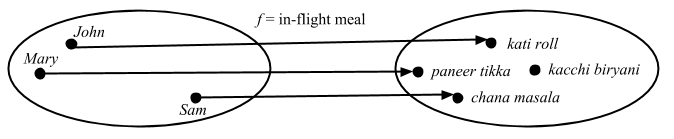

All elements in codomain are mapped only once. We can imagine a third object T, which maps to John, Mary, and Sam. Any of the composition would still land on a unique meal. Here’s the external diagram: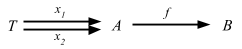

Epimorphism 

Definition: An arrow f with this cancellation property ‘if t₁ ∘ f = t₂ ∘ f then t₁ = t₂’ for every T is called an epimorphism.

Apparently, this is a generalized form of surjective, but the book doesn’t go into detail, so I’ll skip over.

Idempotent 

Definition: An endomorphism e is called idempotent if e ∘ e = e.

Automorphism 

An arrow, which is both an endomorphism and at the same time an isomorphism, usually called by one word automorphism.

I think we’ve covered enough ground. Breaking categories apart into internal diagrams really helps getting the hang of it.