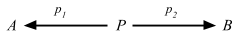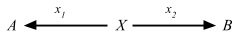Products 

Let us begin by considering products of sets. Given sets A and B, the cartesian product of A and B is the set of ordered pairs
A × B = {(a, b)| a ∈ A, b ∈ B}

There are two coordinate projections:

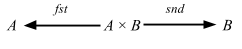
with:

• fst ∘ (a, b) = a
• snd ∘ (a, b) = b

This notion of product relates to scala.Product, which is the base trait for all tuples and case classes.

For any element in c ∈ A × B, we have c = (fst ∘ c, snd ∘ c)

Using the same trick as yesterday, we can introduce the singleton explicitly:

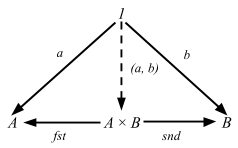
The (external) diagram captures what we stated in the above. If we replace 1-elements by generalized elements, we get the categorical definition.

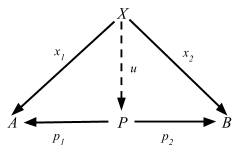
Definition 2.15. In any category C, a product diagram for the objects A and B consists of an object P and arrows p₁ and p₂

satisfying the following UMP:

Given any diagram of the form

there exists a unique u: X => P, making the diagram

commute, that is, such that x₁ = p₁ u and x₂ = p₂ u.

Because this is universal, this applies to any category.

Uniqueness of products 

UMP also suggests that all products of A and B are unique up to isomorphism.

Proposition 2.17 Products are unique up to isomorphism.

Suppose we have P and Q that are products of objects A and B.

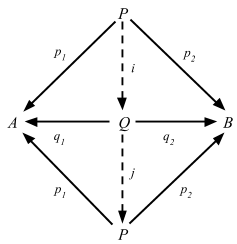
1. Because P is a product, there is a unique i: P => Q such that p₁ = q₁ ∘ i and p₂ = q₂ ∘ i
2. Because Q is a product, there is a unique j: Q => P such that q₁ = p₁ ∘ j and q₂ = p₂ ∘ j
3. By composing j and i we get 1_P = j ∘ i
4. Similarly, we can also get 1_Q = i ∘ j
5. Thus i is an isomorphism, and P ≅ Q ∎

Since all products are isometric, we can just denote one as A × B, and the arrow u: X => A × B is denoted as ⟨x₁, x₂⟩.

Examples 

We saw that in Sets, cartesian product is a product.

Let P be a poset and consider a product of elements p, q ∈ P. We must have projections

• p × q ≤ p
• p × q ≤ q

and if for any element x, x ≤ p, and x ≤ q
then we need

• x ≤ p × q

In this case, p × q becomes greatest lower bound.