Initial and terminal objects 

Let’s look at something abstract. When a definition relies only on category theoretical notion (objects and arrows), it often reduces down to a form “given a diagram abc, there exists a unique x that makes another diagram xyz commute.” Commutative in this case mean that all the arrows compose correctly.Those defenitions are called universal property or universal mapping property (UMP).

Some of the notions have a counterpart in set theory, but it’s more powerful because of its abtract nature. Consider making the empty set and the one-element sets in Sets abstract.

Definition 2.9. In any category C, an object

• 0 is initial if for any object C there is a unique morphism
  0 => C
• 1 is terminal if for any object C there is a unique morphism
  C => 1

Uniquely determined up to isomorphism 

As a general rule, the uniqueness requirements of universal mapping properties are required only up to isomorphisms. Another way of looking at it is that if objects A and B are isomorphic to each other, they are “equal in some sense.” To signify this, we write A ≅ B.

Proposition 2.10 Initial (terminal) objects are unique up to isomorphism.
Proof. In fact, if C and C’ are both initial (terminal) in the same category, then there’s a unique isomorphism C => C’. Indeed, suppose that 0 and 0’ are both initial objects in some category C; the following diagram then makes it clear that 0 and 0’ are uniquely isomorphic:

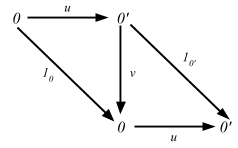
Given that isomorphism is defined by g ∘ f = 1_A and f ∘ g = 1_B, this looks good.

Examples 

In Sets, the empty set is initial and any singleton set {x} is terminal.

So apparently there’s a concept called an empty function that maps from an empty set to any set.

In a poset, an object is plainly initial iff it is the least element, and terminal iff it is the greatest element.

This kind of makes sense, since in a poset we need to preserve the structure using ≤.

There are many other examples, but the interesting part is that seemingly unrelated concepts share the same structure.