始対象と終対象 

ちょっと抽象的なものを見ていこう。定義が圏論的な概念 (対象と射) のみに依存すると、よく「図式 abc が与えられたとき、別の図式 xyz が可換となる (commute) ような唯一の x が存在する」という形式になる。この場合の可換性とは、全ての射が正しく合成できるといった意味だ。このような定義は普遍性 (universal property) または普遍写像性 (universal mapping property) と呼ばれ、英語だと長いので UMP と略される。

集合論から来る概念もあるけども、抽象的な性質からより強力なものになっている。Sets の空集合と唯一つだけの要素を持つ集合を抽象化することを考えてみる。

定義 2.9 任意の圏 C において、

• 始対象 (initial) 0 は、任意の対象 C に対して以下を満たす一意の射を持つ
  0 => C
• 終対象 (terminal) 1 は、任意の対象 C に対して以下を満たす一意の射を持つ
  C => 1

同型を除いて一意 

普遍写像性一般に言えることとして、一意と言った場合にこの要件は同型を除く (unique up to isomorphism) ということだ。考え方を変えると、もし対象 A と B が同型ならば「何らかの意味で等しい」ということでもある。これを記号化して A ≅ B と表記する。

命題 2.10 全ての始対象 (終対象) は同型を除いて一意である
証明。もし仮に C と C’ が両方とも同じ圏内の任意の始対象 (終対象) であるならば、そこには一意の同型射 C => C’ が存在する。0 と 0’ がある圏 C の始対象であるとする。以下の図式により、0 と 0’ が一意に同型であることは明らか:

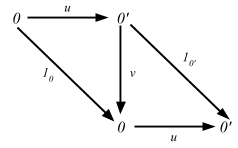
同型射の定義は g ∘ f = 1_A かつ f ∘ g = 1_B なので、確かにこれで合ってる。

例 

Sets 圏において、空集合は始対象であり、任意の単集合 {x} は終対象だ。

どうやら空関数という概念があって、空集合から任意の集合へ関数が出ているらしい。

poset では、対象は最小の要素を持つとき始対象で、最大の要素を持つ場合に終対象となる。

poset では ≤ の構造を保存しなければいけないので、何となく分かる気がする。

他にも多くの例があるけども、面白いのは一見すると無関係な概念が同じ構造を持っているということだ。