決定問題と選択問題 

CM:

1. 決定問題 (determination problem; もしくは extension)
図に表す f と g があるとき、h = g ∘ f が成り立つ g があれば全て挙げよ。

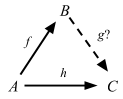
2. 選択問題 (choice problem; もしくは lifting)
図に表す g と h があるとき、h = g ∘ f が成り立つ g があれば全て挙げよ。

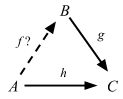
これら 2つの問題は割り算に類似している。

レトラクションとセクション 

定義: f: A => B があるとき、

• r ∘ f = 1_A が成り立つ射 r: B => A をf のレトラクション (retraction) という。
• f ∘ s = 1_B が成り立つ射 s: B => A をf のセクション (section) という。

レトラクション問題の外部図式はこうなる:

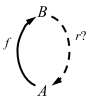
セクション問題の外部図式:

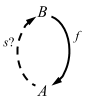
全射 

もし射 f: A => B に関して「任意の射 y: T => B に対して f ∘ x = y が成り立つ射 x: T => A が存在する」という条件が成り立つ場合、「f は T からの射に関して全射 (surjective) である」という。

まずは集合論で全射 (surjective) と言ったときどういう意味なのかを考えるのに独自の例を作ってみた: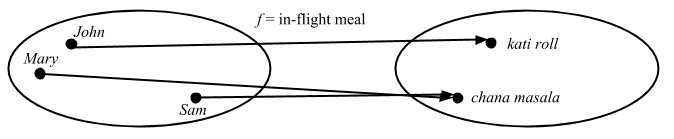

John が友達とインドに行くとして、飛行機の昼食に二つの選択があるとする: チキンラップサンドかスパイシーなヒヨコ豆だ。全射ということは各メニューに対して最低一人はその選択を選んだ人がいるということだ。言い換えると、コドメイン内の要素が網羅されている。

ここで単集合を導入することで要素という考えを一般化できることを思い出してほしい。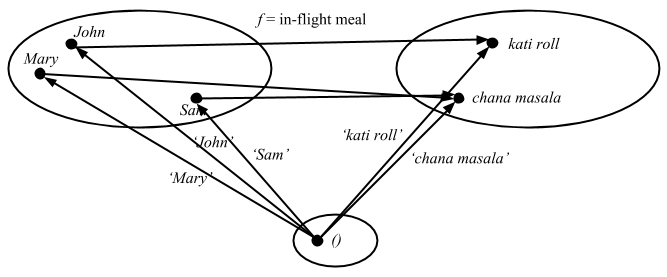

これを圏論での全射の定義と比較してみよう: 任意の射 y: T => B に対して f ∘ x = y が成り立つ射 x: T => A が存在する。どの 1 から B (昼食) への射に対しても、f ∘ x = y が成立する 1 から A (人) への射が存在する。つまり、f は 1 からの射に関して全射であると言える。

これを外部図式で表してみる。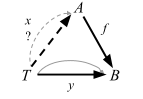

選択問題と同じ形になった。

単射とモノ射 

定義: もし射 f に関して「任意の射のペア x₁: T => A と x₂: T => A に対して f ∘ x₁ = f ∘ x₂ ならば x₁ = x₂ である」という条件が成り立つ場合、「f は T からの射に関して単射 (injective) である」という。

もし f が全ての T からの射に関して単射である場合、f は単射である、またはモノ射 (monomorphism) であるという。

集合論で考えた場合の単射はこうなる:

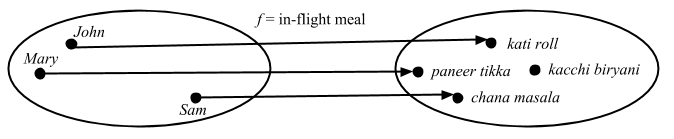
コドメイン内の要素は全て一度だけ写像されている。ここで 3つ目の対象 T を頭の中で想像して、そこから John、Mary、Sam への射が出ているとする。どの射を合成してもユニークな食事へと届くはずだ。外部図式だとこうなる: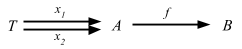

エピ射 

定義: もし射 f に関して「任意の射のペア t₁: T => A と t₂: T => A に対して t₁ ∘ f = t₂ ∘ f ならば t₁ = t₂ である」という条件が全ての T において成り立つ場合、エピ射 (epimorphism) であるという。

これは全射の一般形らしいけども、本ではそこの所をつっこんでないので飛ばすことにする。

冪等射 

定義: 自己準同型射 (endomorphism) について e ∘ e = e が成り立つとき冪等射 (idempotent) という。

冪等の読みはベキトウ。

自己同型射 

自己準同型 (endomorphism) であり、かつ同型 (isomorphism) である射のことを自己同型射 (automorphism) という。

結構進めたので、これぐらいにしておこう。圏という考えが一度内部図式にバラすことで分かりやすくなったと思う。