双対性 

逆圏 

双対性に入る前に、既存の圏から別の圏を生成するということを話しておく必要がある。ここで注意してほしいのは、今まで取り扱ってきた対象ではなくて圏の話をしているということで、これは対象と射の両方を含む。

任意の圏 C の逆圏 (opposite category、また dual「双対圏」とも) C^op は、C と同じ対象を持つが、C^op 内の射は C では f: D => C である。つまり、C^op は C の射を形式的に逆向きにしたものだ。

双対性原理 

この考えをさらに進めて、圏論内の任意の文 Σ の以下を置換して「双対文」Σ^* を得ることができる。

• f ∘ g の代わりに g ∘ f
• コドメインの代わりにドメイン
• ドメインの代わりにコドメイン

意味論的にどれが f で g なのかに重要性は無いため、Σ が圏論のみに基づいているかぎり双対文も成り立つ。そのため、ある概念についての任意の証明はその双対に対しても成り立つ。これは双対性原理 (duality principle) と呼ばれる。

別の見方をすると、もし Σ が全ての圏 C について成り立つとした場合、C^op でも成り立つことになる。そのため、Σ^* は (C^op)^op、つまり C でも成り立つことになる。

始対象と終対象の定義をもう一度見てみよう:

定義 2.9 任意の圏 C において、

• 始対象 (initial) 0 は、任意の対象 C に対して以下を満たす一意の射を持つ
  0 => C
• 終対象 (terminal) 1 は、任意の対象 C に対して以下を満たす一意の射を持つ
  C => 1

これはお互いの双対となっているため、圏 C での始対象は逆圏 C^op での終対象となる。

ここで「全ての始対象は同型を除いて一意である」という命題の定義を思い出してほしい。

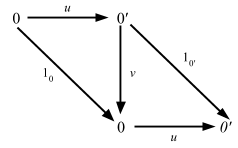
上の図式内の全ての射の方向を逆転すると、終対象に関する証明が得られる。

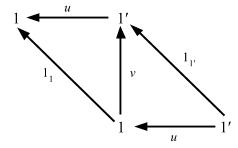
これは結構すごい。