自由モノイド 

すごいHaskellたのしく学ぼうから少し寄り道して、自由対象 (free object) を探索してみる。

まずは自由モノイドからみていこう。以下のような文字の集合があるとする:

A = { 'a', 'b', 'c', ... }

A に関する自由モノイド (fee monoid)、A* を以下のように形成することができる:

A* = String

ここでの2項演算子は String の連結 (concatenation) だ。 空文字 "" を単位元 (identity) として使うことでモノイド則を満たすことを証明できるはずだ。

さらに、任意の集合 A に対しても以下のようにして自由モノイドを形成できる:

A* = List[A]

ここでの2項演算子は ::: で、単位元は Nil だ。 自由モノイド M(A) の定義は以下のように与えられる:

Awodey:

M(A) の普遍写像性 (universal mapping property, UMP)
i: A => |M(A)| という関数があって、 任意のモノイド N と任意の関数 f: A => |N| があるとき、 |f_hom| ∘ i = f を満たす一意の準同型写像 (homomorphism) f_hom = M(A) => N がある。これを図示すると以下のようになる。

A の代わりに X を使って図を書いてみる。なお、|N| は Set[N] という意味だ:

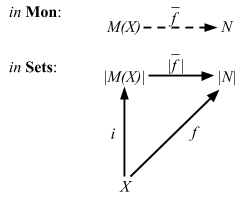
これを Scala を使って考えてみる。

def i(x: X): Set[M[X]] = ???
def f(x: X): Set[N] = ???

// 一意のものが存在する
def f_hom(mx: M[X]): N

// ただし、以下の条件を満たす
def f_hom_set(smx: Set[M[X]]): Set[N] = sma map {f_hom}
f == f_hom_set compose i

ここで A が Char で、N が (Int, +) だとする。 String が自由モノイドを構成するかのプロパティテストを書くことができる。

scala> def i(x: Char): Set[String] = Set(x.toString)
i: (x: Char)Set[String]

scala> def f(x: Char): Set[Int] = Set(x.toInt) // example
f: (x: Char)Set[Int]

scala> val f_hom: PartialFunction[String, Int] =
         { case mx: String if mx.size == 1 => mx.charAt(0).toInt }
f_hom: PartialFunction[String,Int] = <function1>

scala> def f_hom_set(smx: Set[String]): Set[Int] = smx map {f_hom}
f_hom_set: (smx: Set[String])Set[Int]

scala> val g = (f_hom_set _) compose (i _)
g: Char => Set[Int] = <function1>

scala> import org.scalacheck.Prop.forAll
import org.scalacheck.Prop.forAll

scala> val propMAFree = forAll { c: Char => f(c) == g(c) }
propMAFree: org.scalacheck.Prop = Prop

scala> propMAFree.check
+ OK, passed 100 tests.

この実装の f では String は自由みたいだ。

単射 

ここから直観として、任意の f を扱うためには Set[M[X]] は X に関してロスレスである必要があることが分かる。 つまり X からの 2値が M[X] 内の同じ値に写像してはいけないということだ。 代数では、これを Char からの射に対して i が単射 (injective) であるという。

定義: もし射 f に関して「任意の射のペア x₁: T => A と x₂: T => A に対して f ∘ x₁ = f ∘ x₂ ならば x₁ = x₂ である」という条件が成り立つ場合、「f は T からの射に関して単射 (injective) である」という。

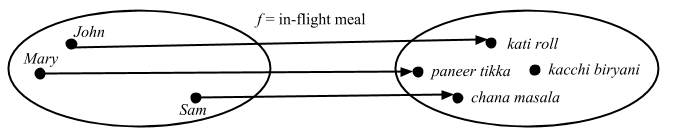
一意性 

UMP は f_hom が一意であることを要請するため、Set[M[A]] が A のゼロ個以上の組み合わせで、それ以外のものは含まないことを要求する。 A に関して M[A] が一意であるため、概念的には集合 A に対して唯一の自由モノイドしか存在しないことになる。 しかし、その自由モノイドは String や List[Char] といったように異なる方法で表現されることもあるため、 実際には自由モノイドの一員といったことになる。

自由対象 

実は、自由モノイドは自由対象 (free object) の一例でしかない。 自由対象は函手 (functor) Set[A]: C[A] => Set[A] を使って以下のように定義できる。

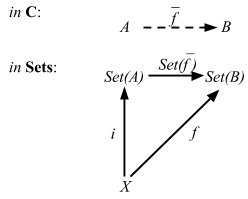
図式を比較すれば、両者ともだいたい似ていることがわかる。