Duality 

Opposite category 

Before we get into duality, we need to cover the concept of generating a category out of an existing one. Note that we are no longer talking about objects, but a category, which includes objects and arrows.

The opposite (or “dual”) category C^op of a category C has the same objects as C, and an arrow f: C => D in C^op is an arrow f: D => C in C. That is, C^op is just C with all of the arrows formally turned around.

The duality principle 

If we take the concept further, we can come up with “dual statement” Σ^* by substituting any sentence Σ in the category theory by replacing the following:

• f ∘ g for g ∘ f
• codomain for domain
• domain for codomain

Since there’s nothing semantically important about which side is f or g, the dual statement also holds true as long as Σ only relies on category theory. In other words, any proof that holds for one concept also holds for its dual. This is called the duality principle.

Another way of looking at it is that if Σ holds in all C, it should also hold in C^op, and so Σ^* should hold in (C^op)^op, which is C.

Let’s look at the definitions of initial and terminal again:

Definition 2.9. In any category C, an object

• 0 is initial if for any object C there is a unique morphism
  0 => C
• 1 is terminal if for any object C there is a unique morphism
  C => 1

They are dual to each other, so the initials in C are terminals in C^op.

Recall proof for “the initial objects are unique up to isomorphism.”

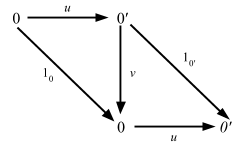
If you flip the direction of all arrows in the above diagram, you do get a proof for terminals.

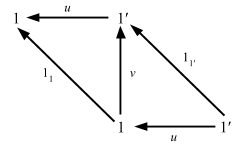
This is pretty cool.