Initial and terminal objects 

When a definition relies only on category theoretical notion (objects and arrows), it often reduces down to a form “given a diagram abc, there exists a unique x that makes another diagram xyz commute.” Commutative in this case mean that all the arrows compose correctly. Such defenition is called a universal property or a universal mapping property (UMP).

Some of the notions have a counterpart in set theory, but it’s more powerful because of its abtract nature. Consider making the empty set and the one-element sets in Sets abstract.

Definition 2.9. In any category C, an object

• 0 is initial if for any object C there is a unique morphism
  
• 1 is terminal if for any object C there is a unique morphism
  

The two diagrams look almost too simple to understand, but the definitions are examples of UMP. The first one is saying that given the diagram, and so if 0 exists, the arrow 0 => C is unique.

Uniquely determined up to isomorphism 

As a general rule, the uniqueness requirements of universal mapping properties are required only up to isomorphisms. Another way of looking at it is that if objects A and B are isomorphic to each other, they are “equal in some sense.” To signify this, we write A ≅ B.

Proposition 2.10 Initial (terminal) objects are unique up to isomorphism.
Proof. In fact, if C and C’ are both initial (terminal) in the same category, then there’s a unique isomorphism C => C’. Indeed, suppose that 0 and 0’ are both initial objects in some category C; the following diagram then makes it clear that 0 and 0’ are uniquely isomorphic:

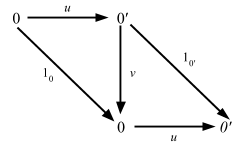
Given that isomorphism is defined by g ∘ f = 1_A and f ∘ g = 1_B, this looks good.

Examples of initial objects 

An interest aspect of abstract construction is that they can show up in different categories in different forms.

In Sets, the empty set is initial and any singleton set {x} is terminal.

Recall that we can encode Set using types and functions between them. In Scala, the uninhabited type might be Nothing, so we’re saying that there is only one function between Nothing to A. According to Milewski, there’s a function in Haskell called absurd. Our implementation might look like this:

def absurd[A]: Nothing => A = { case _ => ??? }

absurd[Int]
// res0: Function1[Nothing, Int] = <function1>

Given that there’s no value in the domain of the function, the body should never be executed.

In a poset, an object is plainly initial iff it is the least element, and terminal iff it is the greatest element.

This kind of makes sense, since in a poset we need to preserve the structure using ≤.

Examples of terminal objects 

A singleton set means it’s a type that has only one possible value. An example of that in Scala would be Unit. There can be only one possible implementation from general A to Unit:

def unit[A](a: A): Unit = ()

unit(1)

This makes Unit a terminal object in the category of Sets, but note that we can define singleton types all we want in Scala using object:

case object Single
def single[A](a: A): Single.type = Single

single("test")
// res2: Single.type = Single

As noted above, in a poset, an object is terminal iff it is the greatest element.