Monoid as categories 

Awodey:

A monoid (sometimes called a semigroup with unit) is a set M equipped with a binary operation ·: M × M => M and a distinguished “unit” element u ∈ M such that for all x, y, z ∈ M,

• x · (y · z) = (x · y) · z
• u · x = x = x · u

Equivalently, a monoid is a category with just one object. The arrows of the category are the elements of the monoid. In particular, the identity arrow is the unit element u. Composition of arrows is the binary operation m · n for the monoid.

See Monoid from day 4 for how Monoid is encoded in Cats.

trait Monoid[@sp(Int, Long, Float, Double) A] extends Any with Semigroup[A] {
  def empty: A

  ....
}

trait Semigroup[@sp(Int, Long, Float, Double) A] extends Any with Serializable {
  def combine(x: A, y: A): A

  ....
}

Here is addition of Int and 0:

scala> 10 |+| Monoid[Int].empty
res26: Int = 10

The idea that these monoids are categories with one object and that elements are arrows used to sound so alien to me, but now it’s a bit more understandable since we were exposed to singleton.

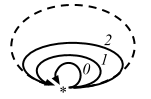
Note in the above monoid (Int, +), arrows are literally 0, 1, 2, etc, and that they are not functions.

Mon 

There’s another category related to monoids. The category of monoids and functions that preserve the monoid structure is denoted by Mon. These arrows that preserve structure are called homomorphism.

In detail, a homomorphism from a monoid M to a monoid N is a function h: M => N such that for all m, n ∈ M,

• h(m ·_M n) = h(m) ·_N h(n)
• h(u_M) = u_N

Since a monoid is a category, a monoid homomorphism is a special case of functors.