Basic category theory 

The most accessible category theory book I’ve come across is Lawvere and Schanuel’s Conceptual Mathematics: A First Introduction to Categories 2nd ed. The book mixes Articles, which is written like a normal textbook; and Sessions, which is kind of written like a recitation class.

Even in the Article section, Lawvere uses many pages to go over the basic concept compared to other books, which is good for self learners.

Sets, arrows, composition 

Lawvere:

Before giving a precise definition of ‘category’, we should become familiar with one example, the category of finite sets and maps. An object in this category is a finite set or collection. … You are probably familiar with some notations for finite sets:

{ John, Mary, Sam }

There are two ways that I can think of to express this in Scala. One is by using a value a: Set[Person]:

sealed trait Person {}
case object John extends Person {}
case object Mary extends Person {}
case object Sam extends Person {}

val a: Set[Person] = Set[Person](John, Mary, Sam)
// a: Set[Person] = Set(John, Mary, Sam)

Another way of looking at it, is that Person as the type is a finite set already without Set. Note: In Lawvere uses the term “map”, but I’m going to change to arrow like Mac Lane and others.

A arrow f in this cateogry consists of three things:

1. a set A, called the domain of the arrow,
2. a set B, called the codomain of the arrow,
3. a rule assigning to each element a in the domain, an element b in the codomain. This b is denoted by f ∘ a (or sometimes ’f(a)‘), read ’f of a‘.

(Other words for arrow are ‘function’, ‘transformation’, ‘operator’, ‘map’, and ‘morphism’.)

Let’s try implementing the favorite breakfast arrow.

sealed trait Breakfast {}
case object Eggs extends Breakfast {}
case object Oatmeal extends Breakfast {}
case object Toast extends Breakfast {}
case object Coffee extends Breakfast {}

lazy val favoriteBreakfast: Person => Breakfast = {
  case John => Eggs
  case Mary => Coffee
  case Sam  => Coffee
}

Note here that an “object” in this category is Set[Person] or Person, but the “arrow” favoriteBreakfast accepts a value whose type is Person. Here’s the internal diagram of the arrow.

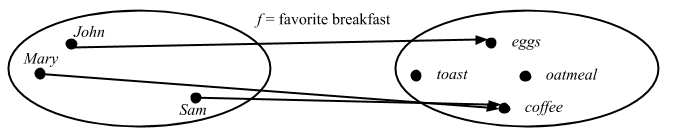
The important thing is: For each dot in the domain, we have exactly one arrow leaving, and the arrow arrives at some dot in the codomain.

I get that a map can be more general than Function1[A, B] but it’s ok for this category. Here’s the implementation of favoritePerson:

lazy val favoritePerson: Person => Person = {
  case John => Mary
  case Mary => John
  case Sam  => Mary
}

An arrow in which the domain and codomain are the same object is called an endomorphism.

An arrow, in which the domain and codomain are the same set A, and for each of a in A, f(a) = a, is called an identity arrow.

The “identity arrow on A” is denoted as 1_A.

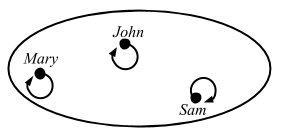
Again, identity is an arrow, so it works on an element in the set, not the set itself. So in this case we can just use scala.Predef.identity.

identity(John)
// res0: John.type = John

Here are the external diagrams corresponding to the three internal diagrams from the above.

This reiterates the point that in the category of finite sets, the “objects” translate to types like Person and Breakfast, and arrows translate to functions like Person => Person. The external diagram looks a lot like the type-level signatures like Person => Person.

The final basic ingredient, which is what lends all the dynamics to the notion of category is composition of arrows, by which two arrows are combined to obtain a third arrow.

We can do this in scala using scala.Function1’s andThen or compose.

lazy val favoritePersonsBreakfast = favoriteBreakfast compose favoritePerson

Here’s the internal diagram:

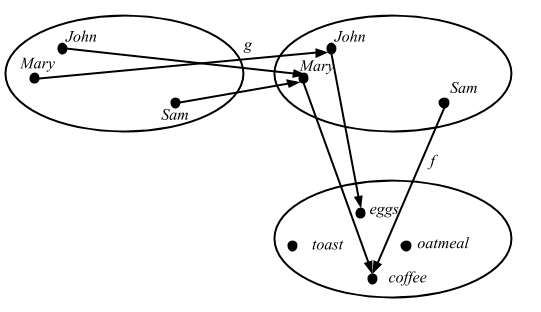
and the external diagram:

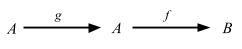
After composition the external diagram becomes as follows:

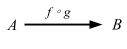
’f ∘ g’ is read ’f following g‘, or sometimes ’f of g‘.

Data for a category consists of the four ingredients:

• objects: A, B, C, …
• arrows: f: A => B
• identity arrows: 1_A: A => A
• composition of arrows

These data must satisfy the following rules:

The identity laws:

• If 1_A: A => A, g: A => B, then g ∘ 1_A = g
• If f: A => B, 1_B: B => B, then 1_A ∘ f = f

The associative law:

• If f: A => B, g: B => C, h: C => D, then h ∘ (g ∘ f) = (h ∘ g) ∘ f

Point 

Lawvere:

One very useful sort of set is a ‘singleton’ set, a set with exactly one element. Fix one of these, say {me}, and call this set ’1‘.

Definition: A point of a set X is an arrows 1 => X. … (If A is some familiar set, an arrow from A to X is called an ’A-element’ of X; thus ’1-elements’ are points.) Since a point is an arrow, we can compose it with another arrow, and get a point again.

If I understand what’s going on, it seems like Lawvere is redefining the concept of the element as a special case of arrow. Another name for singleton is unit set, and in Scala it is (): Unit. So it’s analogous to saying that values are sugar for Unit => X.

lazy val johnPoint: Unit => Person = { case () => John }
lazy val johnFav = favoriteBreakfast compose johnPoint

johnFav(())
// res1: Breakfast = Eggs

Session 2 and 3 contain nice review of Article I, so you should read them if you own the book.