Cat 

Awodey:

Definition 1.2. A functor
F: C => D
between categories C and D is a mapping of objects to objects and arrows to arrows, in such a way that.

• F(f: A => B) = F(f): F(A) => F(B)
• F(1_A) = 1_F(A)
• F(g ∘ f) = F(g) ∘ F(f)

That is, F, preserves domains and codomains, identity arrows, and composition.

Now we are talking. Functor is an arrow between two categories. Here’s the external diagram:

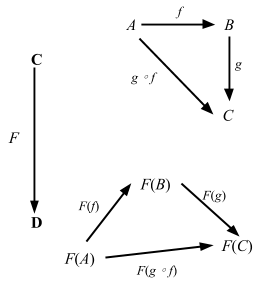
The fact that the positions of F(A), F(B), and F(C) are distorted is intentional. That’s what F is doing, slightly distorting the picture, but still preserving the composition.

This category of categories and functors is denoted as Cat.

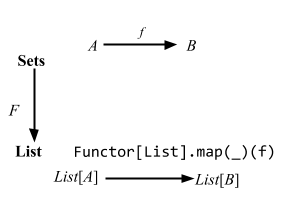
Let me remind you of the typographical conventions. The italic uppercase A, B, and C represent objects (which in case of Sets corresponds to types like Int and String). On the other hand, the bold uppercase C and D represent categories. Categories can be all kinds of things, including the datatypes we’ve seen ealier like List[A]. So a functor F: C => D is not some function, it’s an arrow between two categories.

In that sense, the way programmers use the term Functor is an extremely limited variety of the functor where C is hardcoded to Sets.