1. 圏論の初歩

圏論の初歩 

僕が見た限りで最も取っ付きやすい圏論の本は Lawvere と Schanuel 共著の Conceptual Mathematics: A First Introduction to Categories 第二版だ。この本は普通の教科書のように書かれた Article という部分と Session と呼ばれる質疑や議論を含めた授業を書き取ったような解説の部分を混ぜた構成になっている。

Article の部分でも他の本と比べて基本的な概念に多くのページをさいて丁寧に解説しているので、独習者向けだと思う。

集合、射、射の合成 

Conceptual Mathematics (以下 Lawvere) の和訳が無いみたいなので、僕の勝手訳になる。訳語の選択などを含め @9_ties の2013年 圏論勉強会 資料を参考にした。この場を借りてお礼します:

「圏」(category) の正確な定義を与える前に、有限集合と射という圏の一例にまず慣れ親しむべきだ。 この圏の対象 (object) は有限集合 (finite set) 別名 collection だ。 … 恐らくこのような有限集合の表記法を見たことがあるだろう: 

{ John, Mary, Sam }

これは Scala だと 2通りの方法で表現できると思う。まずは a: Set[Person] という値を使った方法: 

sealed trait Person {}
case object John extends Person {}
case object Mary extends Person {}
case object Sam extends Person {}

val a: Set[Person] = Set[Person](John, Mary, Sam)
// a: Set[Person] = Set(John, Mary, Sam)

もう一つの考え方は、Person という型そのものが Set を使わなくても既に有限集合となっていると考えることだ。注意: Lawvere では map という用語を使っているけども、Mac Lane や他の本に合わせて本稿では arrow を英語での用語として採用する。

この圏の射 (arrow) f は以下の3つから構成される

  1. 集合 A。これは射のドメイン (domain) と呼ばれる。
  2. 集合 B。これは射のコドメイン (codomain) と呼ばれる。
  3. ドメイン内のそれぞれの要素 (element, 元とも言う) a に対してコドメイン内の元 b を割り当てるルール。この b は f ∘ a (または f(a)) と表記され、「f　マル a」と読む。

(射の他にも 「矢」、「写像」(map)、「函数」(function)、「変換」(transformation)、「作用素」(operator)、morphism などの言葉が使われることもある。)

好みの朝食の射を実装してみよう。 

sealed trait Breakfast {}
case object Eggs extends Breakfast {}
case object Oatmeal extends Breakfast {}
case object Toast extends Breakfast {}
case object Coffee extends Breakfast {}

lazy val favoriteBreakfast: Person => Breakfast = {
  case John => Eggs
  case Mary => Coffee
  case Sam  => Coffee
}

この圏の「対象」は Set[Person] か Person であるのに対して、「射」の favoriteBreakfast は型が Person である値を受け取ることに注意してほしい。以下がこの射の内部図式 (internal diagram) だ。
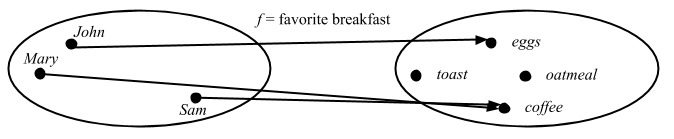
favorite breakfast

大切なのは、ドメイン内のそれぞれの黒丸から正確に一本の矢印が出ていて、その矢印がコドメイン内の何らかの黒丸に届いていることだ。

射が Function1[A, B] よりも一般的なものだということは分かるが、この圏の場合はこれで十分なので良しとする。これが favoritePerson の実装となる: 

lazy val favoritePerson: Person => Person = {
  case John => Mary
  case Mary => John
  case Sam  => Mary
}

ドメインとコドメインが同一の対象の射を自己準同型射 (endomorphism) と呼ぶ。

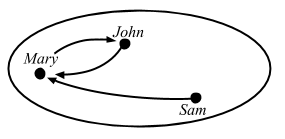
favorite person

ドメインとコドメインが同一の集合 A で、かつ A 内の全ての a において f(a) = a であるものを恒等射 (identity arrow) と言う。

「A の恒等射」は 1A と表記する。
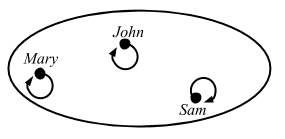
identity arrow

恒等射は射であるため、集合そのものというよりは集合の要素にはたらく。そのため、scala.Predef.identity を使うことができる。 

identity(John)
// res0: John.type = John

上の 3つの内部図式に対応した外部図式 (external diagram) を見てみよう。
external diagrams

この図式を見て再び思うのは有限集合という圏においては、「対象」は Person や Breakfast のような型に対応して、射は Person => Person のような関数に対応するということだ。外部図式は Person => Person というような型レベルでのシグネチャに似ている。

圏の概念の最後の基礎部品で、圏の変化を全て担っているのが射の合成 (composition of maps) だ。これによって 2つの射を組み合わせて 3つ目の射を得ることができる。

Scala なら scala.Function1 の andThen か compose を使うことができる。 

lazy val favoritePersonsBreakfast = favoriteBreakfast compose favoritePerson

これが内部図式だ:
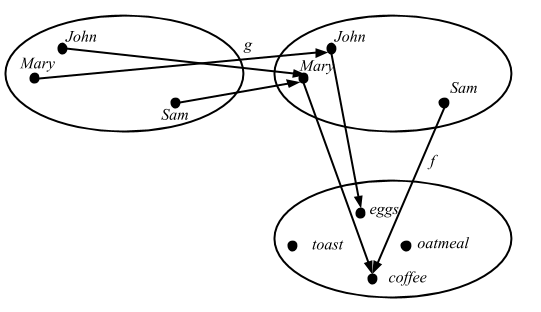
composition of arrows

そして外部図式:
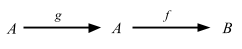
external diagram: composition of arrows

射を合成すると外部図式はこうなる:
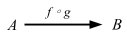
external diagram: f of g

’f ∘ g’ は「f マル g」、または「f と g の合成射」と読む。

圏のデータは以下の4部品から構成される:

  • 対象 (objects): A, B, C, …
  • 射 (arrows): f: A => B
  • 恒等射 (identity arrows): 1A: A => A
  • 射の合成

これらのデータは以下の法則を満たさなければいけない:

単位元律 (The identity laws):

  • If 1A: A => A, g: A => B, then g ∘ 1A = g
  • If f: A => B, 1B: B => B, then 1A ∘ f = f

結合律 (The associative law):

  • If f: A => B, g: B => C, h: C => D, then h ∘ (g ∘ f) = (h ∘ g) ∘ f

点 

Lawvere:

単集合 (singleton) という非常に便利な集合あって、これは唯一の要素 (element; 元とも) のみを持つ。これを例えば {me} という風に固定して、この集合を 1 と呼ぶ。

定義: ある集合の点 (point) は、1 => X という射だ。

(もし A が既に親しみのある集合なら、A から X への射を X の 「A-要素」という。そのため、「1-要素」は点となる。) 点は射であるため、他の射と合成して再び点を得ることができる。

誤解していることを恐れずに言えば、Lawvere は要素という概念を射の特殊なケースとして再定義しているように思える。単集合 (singleton) の別名に unit set というものがあって、Scala では (): Unit となる。つまり、値は Unit => X の糖衣構文だと言っているのに類似している。 

lazy val johnPoint: Unit => Person = { case () => John }
lazy val johnFav = favoriteBreakfast compose johnPoint

johnFav(())
// res1: Breakfast = Eggs

関数型プログラミングをサポートする言語における第一級関数は、関数を値として扱うことで高階関数を可能とする。圏論は逆方向に統一して値を関数として扱っている。

Session 2 と 3 は Article I の復習を含むため、本を持っている人は是非読んでほしい。

❧
Next page
Arrow
猫番 — 圏論の初歩