Contents
猫番
Cats は Scala のための関数型プログラミングのライブラリで、これは僕がそれを使ってみた記録だ。 大まかな流れは、僕が 2012年 (!) に書いた独習 Scalaz に倣う。
Cats のサイト によると、名前は圏 (category) の遊び心のある短縮形に由来する。 プログラマの取りまとめは猫の群をまとめるようなものだと言われる。
訳注: 本稿原題の herding cats は、英語の慣用句の一つで、herd というのは何十匹もの牛や羊を追い立てて群で移動させること。 猫は集団行動ができないので、言うことを聞かずにてんでんばらばらな状態、またはそれをまとめようとする様。
少なくとも Scala を使ってるプログラマに関しては当てはまるのではないかと思う。 この状況を十分承知した上で、Cats は第一の動機として「とっつき易さ」をあげている。
Cats は技術的な視点からみても面白そうだ。 とっつき易さのせいか、Erik Asheim (@d6/@non) の凄さか、 色々人が集まってきて新しいアイディアを持ち込んでいる。 例えば、Michael Pilquist (@mpilquist) 氏の simulacrum や Miles Sabin (@milessabin) 氏の型クラスの自動導出などが例だ。 これから、色々学んでいきたい。

0日目
これは、僕が Scalaz を独習したログをもとに Cats をいじってみたログだ。 チュートリアルと一部では呼ばれているが、走り書きで書かれたトラベルログだと思って読んだほうがいい。 つまり、実際にここで書かれたことを学びたければ、本を読んだり、自分で例題を解く他に近道は無い。
いきなり詳細に飛び込む代わりに、前編として導入から始めたいと思う。
Cats 入門
Nick Partridge さんが Melbourne Scala Users Group で 2010年3月22日に行った Scalaz のトークをネタとして借用する:
Scalaz talk is up - http://bit.ly/c2eTVR Lots of code showing how/why the library exists
— Nick Partridge (@nkpart) March 28, 2010
Cats は、主に 2つの部分から構成される:
- 新しいデータ型 (
Validated,State, etc) - 実用上必要な多くの汎用関数の実装 (アドホック多相性、trait + implicit)
多相性って何?
パラメータ多相 (parametric polymorphism)
Nick さん曰く:
この関数
headはAのリストを取ってAを返します。Aが何であるかはかまいません。Intでもいいし、Stringでもいいし、OrangeでもCarでもいいです。どのAでも動作し、存在可能な全てのAに対してこの関数は定義されています。
def head[A](xs: List[A]): A = xs(0)
head(1 :: 2 :: Nil)
// res1: Int = 1
case class Car(make: String)
head(Car("Civic") :: Car("CR-V") :: Nil)
// res2: Car = Car(make = "Civic")
Haskell wiki 曰く:
パラメータ多相 (parametric polymorphism) とは、ある値の型が 1つもしくは複数の (制限の無い) 型変数を含むことを指し、その値は型変数を具象型によって置換することによって得られる型ならどれでも採用することができる。
派生型による多態 (subtype polymorphism)
ここで、型 A の 2つの値を足す plus という関数を考える:
def plus[A](a1: A, a2: A): A = ???
型 A によって、足すことの定義を別々に提供する必要がある。これを実現する方法の一つが派生型 (subtyping) だ。
trait PlusIntf[A] {
def plus(a2: A): A
}
def plusBySubtype[A <: PlusIntf[A]](a1: A, a2: A): A = a1.plus(a2)
これで A の型によって異なる plus の定義を提供できるようにはなった。しかし、この方法はデータ型の定義時に Plus を mixin する必要があるため柔軟性に欠ける。例えば、Int や String には使うことができない。
アドホック多相
Scala における3つ目の方法は trait への暗黙の変換か暗黙のパラメータ (implicit parameter) を使うことだ。
trait CanPlus[A] {
def plus(a1: A, a2: A): A
}
def plus[A: CanPlus](a1: A, a2: A): A = implicitly[CanPlus[A]].plus(a1, a2)
これは以下の意味においてまさにアドホックだと言える
- 異なる
Aの型に対して別の関数定義を提供することができる - (
Intのような) 型に対してソースコードへのアクセスが無くても関数定義を提供することができる - 異なるスコープにおいて関数定義を有効化したり無効化したりできる
この最後の点によって Scala のアドホック多相性は Haskell のそれよりもより強力なものだと言える。このトピックに関しては Debasish Ghosh さん (@debasishg) のScala Implicits: 型クラス、襲来参照。
この plus 関数をより詳しく見ていこう。
sum 関数
アドホック多相の具体例として、Int のリストを合計する簡単な関数 sum を徐々に一般化していく。
def sum(xs: List[Int]): Int = xs.foldLeft(0) { _ + _ }
sum(List(1, 2, 3, 4))
// res0: Int = 10
Monoid
これを少し一般化してみましょう。
Monoidというものを取り出します。… これは、同じ型の値を生成するmappendという関数と「ゼロ」を生成する関数を含む型です。
object IntMonoid {
def mappend(a: Int, b: Int): Int = a + b
def mzero: Int = 0
}
これを代入することで、少し一般化されました。
def sum(xs: List[Int]): Int = xs.foldLeft(IntMonoid.mzero)(IntMonoid.mappend)
sum(List(1, 2, 3, 4))
// res2: Int = 10
次に、全ての型
AについてMonoidが定義できるように、Monoidを抽象化します。これでIntMonoidがIntのモノイドになりました。
trait Monoid[A] {
def mappend(a1: A, a2: A): A
def mzero: A
}
object IntMonoid extends Monoid[Int] {
def mappend(a: Int, b: Int): Int = a + b
def mzero: Int = 0
}
これで sum が Int のリストと Int のモノイドを受け取って合計を計算できるようになった:
def sum(xs: List[Int], m: Monoid[Int]): Int = xs.foldLeft(m.mzero)(m.mappend)
sum(List(1, 2, 3, 4), IntMonoid)
// res4: Int = 10
これで
Intを使わなくなったので、全てのIntを一般型に置き換えることができます。
def sum[A](xs: List[A], m: Monoid[A]): A = xs.foldLeft(m.mzero)(m.mappend)
sum(List(1, 2, 3, 4), IntMonoid)
// res6: Int = 10
最後の変更点は
Monoidを implicit にすることで毎回渡さなくてもいいようにすることです。
def sum[A](xs: List[A])(implicit m: Monoid[A]): A = xs.foldLeft(m.mzero)(m.mappend)
{
implicit val intMonoid = IntMonoid
sum(List(1, 2, 3, 4))
}
// res8: Int = 10
Nick さんはやらなかったけど、この形の暗黙のパラメータは context bound で書かれることが多い:
def sum[A: Monoid](xs: List[A]): A = {
val m = implicitly[Monoid[A]]
xs.foldLeft(m.mzero)(m.mappend)
}
{
implicit val intMonoid = IntMonoid
sum(List(1, 2, 3, 4))
}
// res10: Int = 10
これでどのモノイドのリストでも合計できるようになり、
sum関数はかなり一般化されました。StringのMonoidを書くことでこれをテストすることができます。また、これらはMonoidという名前のオブジェクトに包むことにします。その理由は Scala の implicit 解決ルールです。ある型の暗黙のパラメータを探すとき、Scala はスコープ内を探しますが、それには探している型のコンパニオンオブジェクトも含まれるのです。
trait Monoid[A] {
def mappend(a1: A, a2: A): A
def mzero: A
}
object Monoid {
implicit val IntMonoid: Monoid[Int] = new Monoid[Int] {
def mappend(a: Int, b: Int): Int = a + b
def mzero: Int = 0
}
implicit val StringMonoid: Monoid[String] = new Monoid[String] {
def mappend(a: String, b: String): String = a + b
def mzero: String = ""
}
}
def sum[A: Monoid](xs: List[A]): A = {
val m = implicitly[Monoid[A]]
xs.foldLeft(m.mzero)(m.mappend)
}
sum(List("a", "b", "c"))
// res12: String = "abc"
この関数に直接異なるモノイドを渡すこともできます。例えば、
Intの積算のモノイドのインスタンスを提供してみましょう。
val multiMonoid: Monoid[Int] = new Monoid[Int] {
def mappend(a: Int, b: Int): Int = a * b
def mzero: Int = 1
}
// multiMonoid: Monoid[Int] = repl.MdocSession3@6082c022
sum(List(1, 2, 3, 4))(multiMonoid)
// res13: Int = 24
FoldLeft
Listに関しても一般化した関数を目指しましょう。… そのためには、foldLeft演算に関して一般化します。
object FoldLeftList {
def foldLeft[A, B](xs: List[A], b: B, f: (B, A) => B) = xs.foldLeft(b)(f)
}
def sum[A: Monoid](xs: List[A]): A = {
val m = implicitly[Monoid[A]]
FoldLeftList.foldLeft(xs, m.mzero, m.mappend)
}
sum(List(1, 2, 3, 4))
// res1: Int = 10
sum(List("a", "b", "c"))
// res2: String = "abc"
sum(List(1, 2, 3, 4))(multiMonoid)
// res3: Int = 24
これで先ほどと同様の抽象化を行なって
FoldLeft型クラスを抜き出します。
trait FoldLeft[F[_]] {
def foldLeft[A, B](xs: F[A], b: B, f: (B, A) => B): B
}
object FoldLeft {
implicit val FoldLeftList: FoldLeft[List] = new FoldLeft[List] {
def foldLeft[A, B](xs: List[A], b: B, f: (B, A) => B) = xs.foldLeft(b)(f)
}
}
def sum[M[_]: FoldLeft, A: Monoid](xs: M[A]): A = {
val m = implicitly[Monoid[A]]
val fl = implicitly[FoldLeft[M]]
fl.foldLeft(xs, m.mzero, m.mappend)
}
sum(List(1, 2, 3, 4))
// res5: Int = 10
sum(List("a", "b", "c"))
// res6: String = "abc"
これで Int と List の両方が sum から抜き出された。
Cats の型クラス
上の例における trait の Monoid と FoldLeft は Haskell の型クラスに相当する。Cats は多くの型クラスを提供する。
これらの型クラスの全ては必要な関数だけを含んだ部品に分けられています。ある関数が必要十分なものだけを要請するため究極のダック・タイピングだと言うこともできるでしょう。
メソッド注入 (enrich my library)
Monoidを使ってある型の 2つの値を足す関数を書いた場合、このようになります。
def plus[A: Monoid](a: A, b: A): A = implicitly[Monoid[A]].mappend(a, b)
plus(3, 4)
// res0: Int = 7
これに演算子を提供したい。だけど、1つの型だけを拡張するんじゃなくて、Monoid のインスタンスを持つ全ての型を拡張したい。
Simulacrum を用いて Cats スタイルでこれを行なってみる。
trait Monoid[A] {
def mappend(a: A, b: A): A
def mzero: A
}
object Monoid {
object syntax extends MonoidSyntax
implicit val IntMonoid: Monoid[Int] = new Monoid[Int] {
def mappend(a: Int, b: Int): Int = a + b
def mzero: Int = 0
}
implicit val StringMonoid: Monoid[String] = new Monoid[String] {
def mappend(a: String, b: String): String = a + b
def mzero: String = ""
}
}
trait MonoidSyntax {
implicit final def syntaxMonoid[A: Monoid](a: A): MonoidOps[A] =
new MonoidOps[A](a)
}
final class MonoidOps[A: Monoid](lhs: A) {
def |+|(rhs: A): A = implicitly[Monoid[A]].mappend(lhs, rhs)
}
import Monoid.syntax._
3 |+| 4
// res2: Int = 7
"a" |+| "b"
// res3: String = "ab"
1つの定義から Int と String の両方に |+| 演算子を注入することができた。
標準データ型に対する演算子構文
このテクニックを使って、Cats はごくたまに Option のような標準ライブラリデータ型へのメソッド注入も提供する:
import cats._, cats.syntax.all._
1.some
// res5: Option[Int] = Some(value = 1)
1.some.orEmpty
// res6: Int = 1
しかし、Cats の演算子の大半は型クラスに関連付けられている。
これで Cats の雰囲気がつかめてもらえただろうか。
1 日目
型クラス初級講座
型クラスは、何らかの振る舞いを定義するインターフェイスです。ある型クラスのインスタンスである型は、その型クラスが記述する振る舞いを実装します。
Cats 曰く:
We are trying to make the library modular. It will have a tight core which will contain only the typeclasses and the bare minimum of data structures that are needed to support them. Support for using these typeclasses with the Scala standard library will be in the
stdproject.
ライブラリはモジュラーなものにしたいと思っている。これは、型クラスとそれらを補助する必要最低限のデータ構造だけを含んだタイトなコアを持つ予定だ。これらの型クラスを Scala 標準ライブラリと併用するためのサポートは
stdプロジェクトになる。
Haskell をたのしく学ぶ路線で取りあえず行ってみる。
sbt
Cats を使ってみるための build.sbt はこんな感じになる:
val catsVersion = "2.4.2"
val catsCore = "org.typelevel" %% "cats-core" % catsVersion
val catsFree = "org.typelevel" %% "cats-free" % catsVersion
val catsLaws = "org.typelevel" %% "cats-laws" % catsVersion
val catsMtl = "org.typelevel" %% "cats-mtl-core" % "0.7.1"
val simulacrum = "org.typelevel" %% "simulacrum" % "1.0.1"
val kindProjector = compilerPlugin("org.typelevel" % "kind-projector" % "0.11.3" cross CrossVersion.full)
val resetAllAttrs = "org.scalamacros" %% "resetallattrs" % "1.0.0"
val munit = "org.scalameta" %% "munit" % "0.7.22"
val disciplineMunit = "org.typelevel" %% "discipline-munit" % "1.0.6"
ThisBuild / scalaVersion := "2.13.5"
lazy val root = (project in file("."))
.settings(
organization := "com.example",
name := "something",
libraryDependencies ++= Seq(
catsCore,
catsFree,
catsMtl,
simulacrum,
kindProjector,
resetAllAttrs,
catsLaws % Test,
munit % Test,
disciplineMunit % Test,
),
scalacOptions ++= Seq(
"-deprecation",
"-encoding", "UTF-8",
"-feature",
"-language:_"
)
)
sbt 1.4.9 を用いて REPL を開く:
$ sbt
> console
[info] Starting scala interpreter...
Welcome to Scala 2.13.5 (OpenJDK 64-Bit Server VM, Java 1.8.0_232).
Type in expressions for evaluation. Or try :help.
scala>
Cats の API ドキュメント もある。
Eq
LYAHFGG:
Eqは等値性をテストできる型に使われます。Eq のインスタンスが定義すべき関数は==と/=です。
Cats で Eq 型クラスと同じものも Eq と呼ばれている。
Eq は non/algebra から cats-kernel というサブプロジェクトに移行して、Cats の一部になった:
import cats._, cats.syntax.all._
1 === 1
// res0: Boolean = true
1 === "foo"
// error: type mismatch;
// found : String("foo")
// required: Int
// 1 === "foo"
// ^^^^^
(Some(1): Option[Int]) =!= (Some(2): Option[Int])
// res2: Boolean = true
標準の == のかわりに、Eq は === と =!= 演算を可能とする。主な違いは Int と String と比較すると === はコンパイルに失敗することだ。
algebra では neqv は eqv に基いて実装されている。
/**
* A type class used to determine equality between 2 instances of the same
* type. Any 2 instances `x` and `y` are equal if `eqv(x, y)` is `true`.
* Moreover, `eqv` should form an equivalence relation.
*/
trait Eq[@sp A] extends Any with Serializable { self =>
/**
* Returns `true` if `x` and `y` are equivalent, `false` otherwise.
*/
def eqv(x: A, y: A): Boolean
/**
* Returns `false` if `x` and `y` are equivalent, `true` otherwise.
*/
def neqv(x: A, y: A): Boolean = !eqv(x, y)
....
}
これは多相性 (polymorphism) の例だ。型の A にとって等価性が何を意味しようと、
neqv はその逆だと定義されている。それが String でも Int でも変わらない。
別の言い方をすれば、Eq[A] が与えられたとき、=== は普遍的に =!= の逆だ。
気になるのが、Eq では等価 (equal) と同値 (equivalent) を同じように使っているフシがあることだ。
同値関係は例えば、「同じ誕生日を持つ」関係も含むのに対して、
等価性は代入原理を要請する。
Order
LYAHFGG:
Ordは、何らかの順序を付けられる型のための型クラスです。Ordはすべての標準的な大小比較関数、>、<、>=、<=をサポートします。
Cats で Ord に対応する型クラスは Order だ。
// plain Scala
1 > 2.0
// res0: Boolean = false
import cats._, cats.syntax.all._
1 compare 2.0
// error: type mismatch;
// found : Double(2.0)
// required: Int
// 1.0 compare 2.0
// ^^^
import cats._, cats.syntax.all._
1.0 compare 2.0
// res2: Int = -1
1.0 max 2.0
// res3: Double = 2.0
Order は Int (負、ゼロ、正) を返す compare 演算を可能とする。
また、minx と max 演算子も可能とする。
Eq 同様、Int と Double の比較はコンパイルを失敗させる。
PartialOrder
Order の他に、Cats は PartialOrder も定義する。
import cats._, cats.data._, cats.implicits._
1 tryCompare 2
// res0: Option[Int] = Some(value = -1)
1.0 tryCompare Double.NaN
// res1: Option[Int] = Some(value = -1)
PartialOrder は Option[Int] を返す tryCompare 演算を可能とする。
algebra によると、オペランドが比較不能な場合は None を返すとのことだ。
だけど、1.0 と Double.NaN を比較しても Some(-1) を返しているので、何が比較不能なのかは不明だ。
def lt[A: PartialOrder](a1: A, a2: A): Boolean = a1 <= a2
lt(1, 2)
// res2: Boolean = true
lt[Int](1, 2.0)
// error: type mismatch;
// found : Double(2.0)
// required: Int
// lt[Int](1, 2.0)
// ^^^
PartialOrder は他にも >, >=, <, そして <=
演算子を可能とするが、これらは気をつけないと標準の比較演算子を使うことになるのでトリッキーだ。
Show
LYAHFGG:
ある値は、その値が
Show型クラスのインスタンスになっていれば、文字列として表現できます。
Cats で Show に対応する型クラスは Show だ:
import cats._, cats.syntax.all._
3.show
// res0: String = "3"
"hello".show
// res1: String = "hello"
これが型クラスのコントラクトだ:
@typeclass trait Show[T] {
def show(f: T): String
}
Scala には既に Any に toString があるため、Show
を定義するのは馬鹿げているように一見見えるかもしれない。
Any ということは逆に何でも該当してしまうので、型安全性を失うことになる。
toString は何らかの親クラスが書いたゴミかもしれない:
(new {}).toString
// res2: String = "repl.MdocSession1@b3c274f"
(new {}).show
// error: value show is not a member of AnyRef
// (new {}).show
// ^^^^^^^^^^^^
object Show は Show のインスタンスを作成するための 2つの関数を提供する:
object Show {
/** creates an instance of [[Show]] using the provided function */
def show[A](f: A => String): Show[A] = new Show[A] {
def show(a: A): String = f(a)
}
/** creates an instance of [[Show]] using object toString */
def fromToString[A]: Show[A] = new Show[A] {
def show(a: A): String = a.toString
}
implicit val catsContravariantForShow: Contravariant[Show] = new Contravariant[Show] {
def contramap[A, B](fa: Show[A])(f: B => A): Show[B] =
show[B](fa.show _ compose f)
}
}
使ってみる:
case class Person(name: String)
case class Car(model: String)
{
implicit val personShow = Show.show[Person](_.name)
Person("Alice").show
}
// res4: String = "Alice"
{
implicit val carShow = Show.fromToString[Car]
Car("CR-V")
}
// res5: Car = Car(model = "CR-V")
Read
LYAHFGG:
ReadはShowと対をなす型クラスです。read関数は文字列を受け取り、Readのインスタンスの型の値を返します。
これは対応する Cats での型クラスを見つけることができなかった。
個人的には Read とその変種である ReadJs をしばしば定義している。
stringly typed programming (strongly typed をもじった造語で、データ構造の代わりに String を使ったコード)
は醜いものだ。
しかし、同時に文字列はプラットフォームの境界に対して堅固なデータ・フォーマットであり (例、 JSON)、
また人が直接扱うことができる (例、コマンドラインオプション)。
そのため、文字列パーシングを避けるのは難しいだろう。
どうしてもやらなければならないのならば、Read はそれを楽にする。
Enum
LYAHFGG:
Enumのインスタンスは、順番に並んだ型、つまり要素の値を列挙できる型です。Enum型クラスの主な利点は、その値をレンジの中で使えることです。また、Enumのインスタンスの型には後者関数succと前者関数predも定義されます。
これは対応する Cats での型クラスを見つけることができなかった。
これは、Enum でも範囲でもないが、non/spire には Interval と呼ばれる面白いデータ構造がある。
nescala 2015 での Erik のトーク、Intervals: Unifying Uncertainty, Ranges, and Loops を見てほしい。
Numeric
LYAHFGG:
Numは数の型クラスです。このインスタンスは数のように振る舞います。
これは対応する Cats での型クラスを見つけることができなかったが、
spire は Numeric を定義する。Cats は、Bounds も定義しない。
これまで、色々と Cats では定義されていない型クラスをみていきた。 Cats の設計目標としてタイトなコアを作ることにあるため、これは必ずしも悪いことではない。
型クラス中級講座
Haskell の文法に関しては飛ばして第8章の型や型クラスを自分で作ろう まで行こう (本を持っている人は第7章)。
信号の型クラス
data TrafficLight = Red | Yellow | Green
これを Scala で書くと:
import cats._, cats.syntax.all._
sealed trait TrafficLight
object TrafficLight {
case object Red extends TrafficLight
case object Yellow extends TrafficLight
case object Green extends TrafficLight
}
これに Eq のインスタンスを定義する。
implicit val trafficLightEq: Eq[TrafficLight] =
new Eq[TrafficLight] {
def eqv(a1: TrafficLight, a2: TrafficLight): Boolean = a1 == a2
}
// trafficLightEq: Eq[TrafficLight] = repl.MdocSession1@7eb2adb6
注意: 最新の algebra.Equal には Equal.instance と Equal.fromUniversalEquals も定義されている。
Eq を使えるかな?
TrafficLight.Red === TrafficLight.Yellow
// error: value === is not a member of object repl.MdocSession.App.TrafficLight.Red
// TrafficLight.red === TrafficLight.yellow
// ^^^^^^^^^^^^^^^^^^^^
Eq が不変 (invariant) なサブタイプ Eq[A] を持つせいで、Eq[TrafficLight] が検知されないみたいだ。
この問題を回避する方法としては、TrafficLight にキャストするヘルパー関数を定義するという方法がある:
import cats._, cats.syntax.all._
sealed trait TrafficLight
object TrafficLight {
def red: TrafficLight = Red
def yellow: TrafficLight = Yellow
def green: TrafficLight = Green
case object Red extends TrafficLight
case object Yellow extends TrafficLight
case object Green extends TrafficLight
}
{
implicit val trafficLightEq: Eq[TrafficLight] =
new Eq[TrafficLight] {
def eqv(a1: TrafficLight, a2: TrafficLight): Boolean = a1 == a2
}
TrafficLight.red === TrafficLight.yellow
}
// res2: Boolean = false
ちょっと冗長だけども、一応動いた。
2日目
昨日はすごいHaskellたのしく学ぼう を頼りに Eq などの
Cats の型クラスを見てきた。
simulacrum を用いた独自型クラスの定義
LYAHFGG:
JavaScript をはじめ、いくつかの弱く型付けされた言語では、
if式の中にほとんど何でも書くことができます。…. 真理値の意味論が必要なところでは厳密にBool型を使うのが Haskell の流儀ですが、 JavaScript 的な振る舞いを実装してみるのも面白そうですよね!
Scala でモジュラーな型クラスを定義するための従来のステップは以下のうようになっていた:
- 型クラス・コントラクト trait である
Fooを定義する。 - 同名のコンパニオン・オブジェクト
Fooを定義して、implicitlyのように振る舞うapplyや、関数からFooのインスタンスを定義するためのヘルパーメソッドを定義する。 FooOpsクラスを定義して、一項演算子や二項演算子を定義する。FooのインスタンスからFooOpsを implicit に提供するFooSyntaxtrait を定義する。
正直言って、最初のもの以外はほとんどコピーペーストするだけのボイラープレートだ。
ここで登場するのが、Michael Pilquist (@mpilquist) 氏の
simulacrum (シミュラクラム) だ。
@typeclass アノテーションを書くだけで、simulacrum は魔法のように上記の 2-4 をほぼ生成してくれる。
丁度、Cats を全面的に simulacrum化させた Stew O’Connor (@stewoconnor/@stew) 氏の #294
が先日 merge されたばかりだ。
Yes と No の型クラス
とりあえず、truthy 値の型クラスを作れるか試してみよう。
@typeclass アノテーションに注意:
scala> import simulacrum._
scala> :paste
@typeclass trait CanTruthy[A] { self =>
/** Return true, if `a` is truthy. */
def truthy(a: A): Boolean
}
object CanTruthy {
def fromTruthy[A](f: A => Boolean): CanTruthy[A] = new CanTruthy[A] {
def truthy(a: A): Boolean = f(a)
}
}
README によると、マクロによって演算子の enrich 関連コードが色々と生成される:
// これは、生成されたであろうコードの予想。自分で書く必要は無い!
object CanTruthy {
def fromTruthy[A](f: A => Boolean): CanTruthy[A] = new CanTruthy[A] {
def truthy(a: A): Boolean = f(a)
}
def apply[A](implicit instance: CanTruthy[A]): CanTruthy[A] = instance
trait Ops[A] {
def typeClassInstance: CanTruthy[A]
def self: A
def truthy: A = typeClassInstance.truthy(self)
}
trait ToCanTruthyOps {
implicit def toCanTruthyOps[A](target: A)(implicit tc: CanTruthy[A]): Ops[A] = new Ops[A] {
val self = target
val typeClassInstance = tc
}
}
trait AllOps[A] extends Ops[A] {
def typeClassInstance: CanTruthy[A]
}
object ops {
implicit def toAllCanTruthyOps[A](target: A)(implicit tc: CanTruthy[A]): AllOps[A] = new AllOps[A] {
val self = target
val typeClassInstance = tc
}
}
}
ちゃんと動くか確かめるために、Int のインスタンスを定義して、使ってみよう。ゴールは 1.truthy が true を返すことだ:
scala> implicit val intCanTruthy: CanTruthy[Int] = CanTruthy.fromTruthy({
case 0 => false
case _ => true
})
scala> import CanTruthy.ops._
scala> 10.truthy
動いた。これは、かなり便利だ。
ただ一点警告があって、それはコンパイル時にマクロパラダイス・プラグインが必要なことだ。CanTruthy
が一度コンパイルされてしまえば、呼び出す側はマクロパラダイスはいらない。
シンボルを使った演算子
CanTruthy に関しては、注入された演算子は一項演算子で、かつ型クラス・コントラクトの関数と同名のものだった。
simulacrum は @op アノテーションを使うことで、シンボルを使った演算子も定義することができる:
scala> @typeclass trait CanAppend[A] {
@op("|+|") def append(a1: A, a2: A): A
}
scala> implicit val intCanAppend: CanAppend[Int] = new CanAppend[Int] {
def append(a1: Int, a2: Int): Int = a1 + a2
}
scala> import CanAppend.ops._
scala> 1 |+| 2
Functor
LYAHFGG:
今度は、
Functor(ファンクター)という型クラスを見ていきたいと思います。Functorは、全体を写せる (map over) ものの型クラスです。
本のとおり、実装がどうなってるかをみてみよう:
/**
* Functor.
*
* The name is short for "covariant functor".
*
* Must obey the laws defined in cats.laws.FunctorLaws.
*/
@typeclass trait Functor[F[_]] extends functor.Invariant[F] { self =>
def map[A, B](fa: F[A])(f: A => B): F[B]
....
}
このように使うことができる:
import cats._, cats.syntax.all._
Functor[List].map(List(1, 2, 3)) { _ + 1 }
// res0: List[Int] = List(2, 3, 4)
このような用例は関数構文と呼ぶことにする:
@typeclass アノテーションによって自動的に map 関数が map
演算子になることは分かると思う。 fa の所がメソッドの this になって、第2パラメータリストが、
map 演算子のパラメータリストとなる:
// 生成されるコードの予想
object Functor {
trait Ops[F[_], A] {
def typeClassInstance: Functor[F]
def self: F[A]
def map[B](f: A => B): F[B] = typeClassInstance.map(self)(f)
}
}
これは、Scala collection ライブラリの map とかなり近いものに見えるが、
この map は CanBuildFrom の自動変換を行わない。
ファンクターとしての Either
Cats は Either[A, B] の Functor インスタンスを定義する。
(Right(1): Either[String, Int]) map { _ + 1 }
// res1: Either[String, Int] = Right(value = 2)
(Left("boom!"): Either[String, Int]) map { _ + 1 }
// res2: Either[String, Int] = Left(value = "boom!")
上のデモが正しく動作するのは現在の所 Either[A, B] には標準ライブラリでは
map を実装してないということに依存していることに注意してほしい。
例えば、List(1, 2, 3) を例に使った場合は、
Functor[List] の map ではなくて、
リストの実装の map が呼び出されてしまう。
そのため、演算子構文の方が読み慣れていると思うけど、
標準ライブラリが map を実装していないことを確信しているか、
多相関数内で使うか以外は演算子構文は避けた方がいい。
回避策としては関数構文を使うことだ。
ファンクターとしての関数
Cats は Function1 に対する Functor のインスタンスも定義する。
{
val addOne: Int => Int = (x: Int) => x + 1
val h: Int => Int = addOne map {_ * 7}
h(3)
}
// res3: Int = 28
これは興味深い。つまり、map は関数を合成する方法を与えてくれるが、順番が f compose g とは逆順だ。通りで Scalaz は map のエイリアスとして ∘ を提供するわけだ。Function1 のもう1つのとらえ方は、定義域 (domain) から値域 (range) への無限の写像だと考えることができる。入出力に関しては飛ばして Functors, Applicative Functors and Monoids へ行こう (本だと、「ファンクターからアプリカティブファンクターへ」)。
ファンクターとしての関数 …
ならば、型
fmap :: (a -> b) -> (r -> a) -> (r -> b)が意味するものとは?この型は、aからbへの関数と、rからaへの関数を引数に受け取り、rからbへの関数を返す、と読めます。何か思い出しませんか?そう!関数合成です!
あ、すごい Haskell も僕がさっき言ったように関数合成をしているという結論になったみたいだ。ちょっと待てよ。
ghci> fmap (*3) (+100) 1
303
ghci> (*3) . (+100) $ 1
303
Haskell では fmap は f compose g を同じ順序で動作してるみたいだ。Scala でも同じ数字を使って確かめてみる:
(((_: Int) * 3) map {_ + 100}) (1)
// res4: Int = 103
何かがおかしい。fmap の宣言と Cats の map 関数を比べてみよう:
fmap :: (a -> b) -> f a -> f b
そしてこれが Cats:
def map[A, B](fa: F[A])(f: A => B): F[B]
順番が逆になっている。これに関して Paolo Giarrusso (@blaisorblade) 氏が説明してくれた:
これはよくある Haskell 対 Scala の差異だ。
Haskell では、point-free プログラミングをするために、「データ」の引数が通常最後に来る。例えば、
map f listという引数順を利用してmap f . map g . map hと書くことでリストの変換子を得ることができる。 (ちなみに、map は fmap を List ファンクターに限定させたものだ)一方 Scala では、「データ」引数はレシーバとなる。 これは、しばしば型推論にとっても重要であるため、map を関数のメソッドとして定義するのは無理がある。 Scala が
(x => x + 1) map List(1, 2, 3)の型推論を行おうとするのを考えてみてほしい。
これが、どうやら有力な説みたいだ。
関数の持ち上げ
LYAHFGG:
fmapも、関数とファンクター値を取ってファンクター値を返す 2 引数関数と思えますが、そうじゃなくて、関数を取って「元の関数に似てるけどファンクター値を取ってファンクター値を返す関数」を返す関数だと思うこともできます。fmapは、関数a -> bを取って、関数f a -> f bを返すのです。こういう操作を、関数の持ち上げ (lifting) といいます。
ghci> :t fmap (*2)
fmap (*2) :: (Num a, Functor f) => f a -> f a
ghci> :t fmap (replicate 3)
fmap (replicate 3) :: (Functor f) => f a -> f [a]
パラメータ順が逆だということは、この持ち上げ (lifting) ができないということだろうか?
幸いなことに、Cats は Functor 型クラス内に派生関数を色々実装している:
@typeclass trait Functor[F[_]] extends functor.Invariant[F] { self =>
def map[A, B](fa: F[A])(f: A => B): F[B]
....
// derived methods
/**
* Lift a function f to operate on Functors
*/
def lift[A, B](f: A => B): F[A] => F[B] = map(_)(f)
/**
* Empty the fa of the values, preserving the structure
*/
def void[A](fa: F[A]): F[Unit] = map(fa)(_ => ())
/**
* Tuple the values in fa with the result of applying a function
* with the value
*/
def fproduct[A, B](fa: F[A])(f: A => B): F[(A, B)] = map(fa)(a => a -> f(a))
/**
* Replaces the `A` value in `F[A]` with the supplied value.
*/
def as[A, B](fa: F[A], b: B): F[B] = map(fa)(_ => b)
}
見ての通り、lift も入っている!
{
val lifted = Functor[List].lift {(_: Int) * 2}
lifted(List(1, 2, 3))
}
// res5: List[Int] = List(2, 4, 6)
これで {(_: Int) * 2} という関数を List[Int] => List[Int] に持ち上げることができた。
他の派生関数も演算子構文で使ってみる:
List(1, 2, 3).void
// res6: List[Unit] = List((), (), ())
List(1, 2, 3) fproduct {(_: Int) * 2}
// res7: List[(Int, Int)] = List((1, 2), (2, 4), (3, 6))
List(1, 2, 3) as "x"
// res8: List[String] = List("x", "x", "x")
Functor則
LYAHFGG:
すべてのファンクターの性質や挙動は、ある一定の法則に従うことになっています。 … ファンクターの第一法則は、「
idでファンクター値を写した場合、ファンクター値が変化してはいけない」というものです。
Either[A, B] を使って確かめてみる。
val x: Either[String, Int] = Right(1)
// x: Either[String, Int] = Right(value = 1)
assert { (x map identity) === x }
第二法則は、2つの関数
fとgについて、「fとgの合成関数でファンクター値を写したもの」と、「まずg、次にfでファンクター値を写したもの」が等しいことを要求します。
言い換えると、
val f = {(_: Int) * 3}
// f: Int => Int = <function1>
val g = {(_: Int) + 1}
// g: Int => Int = <function1>
assert { (x map (f map g)) === (x map f map g) }
これらの法則は Functor の実装者が従うべき法則で、コンパイラはチェックしてくれない。
Discipline を用いた法則のチェック
コンパイラはチェックしてくれないけども、Cats は Functor則をコードで表現した
FunctorLaws trait を含む:
/**
* Laws that must be obeyed by any [[Functor]].
*/
trait FunctorLaws[F[_]] extends InvariantLaws[F] {
implicit override def F: Functor[F]
def covariantIdentity[A](fa: F[A]): IsEq[F[A]] =
fa.map(identity) <-> fa
def covariantComposition[A, B, C](fa: F[A], f: A => B, g: B => C): IsEq[F[C]] =
fa.map(f).map(g) <-> fa.map(f andThen g)
}
REPL からの法則のチェック
これは ScalaCheck のラッパーである Discipline というライブラリに基いている。 ScalaCheck を使って REPL からテストを実行することができる。
scala> import cats._, cats.syntax.all._
import cats._
import cats.syntax.all._
scala> import cats.laws.discipline.FunctorTests
import cats.laws.discipline.FunctorTests
scala> val rs = FunctorTests[Either[Int, *]].functor[Int, Int, Int]
val rs: cats.laws.discipline.FunctorTests[[?$0$]scala.util.Either[Int,?$0$]]#RuleSet = org.typelevel.discipline.Laws$DefaultRuleSet@2b1a2a1d
scala> import org.scalacheck.Test.Parameters
import org.scalacheck.Test.Parameters
scala> rs.all.check(Parameters.default)
+ functor.covariant composition: OK, passed 100 tests.
+ functor.covariant identity: OK, passed 100 tests.
+ functor.invariant composition: OK, passed 100 tests.
+ functor.invariant identity: OK, passed 100 tests.
rs.all は org.scalacheck.Properties を返し、これは check メソッドを実装する。
Discipline + MUnit を用いた法則のチェック
ScalaCheck の他に ScalaTest、Specs2、MUnit からこれらのテストを呼び出して使うということができる。Either[Int, Int] の Functor則を MUnit でチェックしてみよう:
package example
import cats._
import cats.laws.discipline.FunctorTests
class EitherTest extends munit.DisciplineSuite {
checkAll("Either[Int, Int]", FunctorTests[Either[Int, *]].functor[Int, Int, Int])
}
上の Either[Int, *] という表記は non/kind-projector を使っている。
テストを実行すると、以下のように表示される:
sbt:herding-cats> Test/testOnly example.EitherTest
example.EitherTest:
+ Either[Int, Int]: functor.covariant composition 0.096s
+ Either[Int, Int]: functor.covariant identity 0.017s
+ Either[Int, Int]: functor.invariant composition 0.041s
+ Either[Int, Int]: functor.invariant identity 0.011s
[info] Passed: Total 4, Failed 0, Errors 0, Passed 4
法則を破る
LYAHFGG:
ここで、
Functorのインスタンスなのに、ファンクター則を満たしていないような病的な例を考えてみましょう。
法則を破ってみよう:
package example
import cats._
sealed trait COption[+A]
case class CSome[A](counter: Int, a: A) extends COption[A]
case object CNone extends COption[Nothing]
object COption {
implicit def coptionEq[A]: Eq[COption[A]] = new Eq[COption[A]] {
def eqv(a1: COption[A], a2: COption[A]): Boolean = a1 == a2
}
implicit val coptionFunctor = new Functor[COption] {
def map[A, B](fa: COption[A])(f: A => B): COption[B] =
fa match {
case CNone => CNone
case CSome(c, a) => CSome(c + 1, f(a))
}
}
}
使ってみる:
import cats._, cats.syntax.all._
import example._
(CSome(0, "hi"): COption[String]) map {identity}
// res0: COption[String] = CSome(counter = 1, a = "hi")
これは最初の法則を破っている。検知するには COption[A] の「任意」の値を暗黙に提供する:
package example
import cats._
import cats.laws.discipline.{ FunctorTests }
import org.scalacheck.{ Arbitrary, Gen }
class COptionTest extends munit.DisciplineSuite {
checkAll("COption[Int]", FunctorTests[COption].functor[Int, Int, Int])
implicit def coptionArbiterary[A](implicit arbA: Arbitrary[A]): Arbitrary[COption[A]] =
Arbitrary {
val arbSome = for {
i <- implicitly[Arbitrary[Int]].arbitrary
a <- arbA.arbitrary
} yield (CSome(i, a): COption[A])
val arbNone = Gen.const(CNone: COption[Nothing])
Gen.oneOf(arbSome, arbNone)
}
}
以下のように表示される:
example.COptionTest:
failing seed for functor.covariant composition is 43LA3KHokN6KnEAzbkXi6IijQU91ran9-zsO2JeIyIP=
==> X example.COptionTest.COption[Int]: functor.covariant composition 0.058s munit.FailException: /Users/eed3si9n/work/herding-cats/src/test/scala/example/COptionTest.scala:8
7:class COptionTest extends munit.DisciplineSuite {
8: checkAll("COption[Int]", FunctorTests[COption].functor[Int, Int, Int])
9:
Failing seed: 43LA3KHokN6KnEAzbkXi6IijQU91ran9-zsO2JeIyIP=
You can reproduce this failure by adding the following override to your suite:
override val scalaCheckInitialSeed = "43LA3KHokN6KnEAzbkXi6IijQU91ran9-zsO2JeIyIP="
Falsified after 0 passed tests.
> Labels of failing property:
Expected: CSome(2,-1)
Received: CSome(3,-1)
> ARG_0: CSome(1,0)
> ARG_1: org.scalacheck.GenArities$$Lambda$36505/1702985322@62d7d97c
> ARG_2: org.scalacheck.GenArities$$Lambda$36505/1702985322@18bdc9d7
....
failing seed for functor.covariant identity is a4C-NCiCQEn0lU6F_TXdy5-IZ-XhMYDrC0vipJ3O_tG=
==> X example.COptionTest.COption[Int]: functor.covariant identity 0.003s munit.FailException: /Users/eed3si9n/work/herding-cats/src/test/scala/example/COptionTest.scala:8
7:class COptionTest extends munit.DisciplineSuite {
8: checkAll("COption[Int]", FunctorTests[COption].functor[Int, Int, Int])
9:
Failing seed: RhjRyflmRS-5CYveyf0uAFHuX6mWNm-Z98FVIs2aIVC=
You can reproduce this failure by adding the following override to your suite:
override val scalaCheckInitialSeed = "RhjRyflmRS-5CYveyf0uAFHuX6mWNm-Z98FVIs2aIVC="
Falsified after 1 passed tests.
> Labels of failing property:
Expected: CSome(-1486306630,-1498342842)
Received: CSome(-1486306629,-1498342842)
> ARG_0: CSome(-1486306630,-1498342842)
....
failing seed for functor.invariant composition is 9uQIZNNK_uZksfWg5pRb0VJUIgUtkv9vG9ckZ4UlRwD=
==> X example.COptionTest.COption[Int]: functor.invariant composition 0.005s munit.FailException: /Users/eed3si9n/work/herding-cats/src/test/scala/example/COptionTest.scala:8
7:class COptionTest extends munit.DisciplineSuite {
8: checkAll("COption[Int]", FunctorTests[COption].functor[Int, Int, Int])
9:
Failing seed: 9uQIZNNK_uZksfWg5pRb0VJUIgUtkv9vG9ckZ4UlRwD=
You can reproduce this failure by adding the following override to your suite:
override val scalaCheckInitialSeed = "9uQIZNNK_uZksfWg5pRb0VJUIgUtkv9vG9ckZ4UlRwD="
Falsified after 0 passed tests.
> Labels of failing property:
Expected: CSome(1,2147483647)
Received: CSome(2,2147483647)
> ARG_0: CSome(0,1095768235)
> ARG_1: org.scalacheck.GenArities$$Lambda$36505/1702985322@431263ab
> ARG_2: org.scalacheck.GenArities$$Lambda$36505/1702985322@5afe6566
> ARG_3: org.scalacheck.GenArities$$Lambda$36505/1702985322@ca0deda
> ARG_4: org.scalacheck.GenArities$$Lambda$36505/1702985322@1d7dde37
....
failing seed for functor.invariant identity is RcktTeI0rbpoUfuI3FHdvZtVGXGMoAjB6JkNBcTNTVK=
==> X example.COptionTest.COption[Int]: functor.invariant identity 0.002s munit.FailException: /Users/eed3si9n/work/herding-cats/src/test/scala/example/COptionTest.scala:8
7:class COptionTest extends munit.DisciplineSuite {
8: checkAll("COption[Int]", FunctorTests[COption].functor[Int, Int, Int])
9:
Failing seed: RcktTeI0rbpoUfuI3FHdvZtVGXGMoAjB6JkNBcTNTVK=
You can reproduce this failure by adding the following override to your suite:
override val scalaCheckInitialSeed = "RcktTeI0rbpoUfuI3FHdvZtVGXGMoAjB6JkNBcTNTVK="
Falsified after 0 passed tests.
> Labels of failing property:
Expected: CSome(2147483647,1054398067)
Received: CSome(-2147483648,1054398067)
> ARG_0: CSome(2147483647,1054398067)
....
[error] Failed: Total 4, Failed 4, Errors 0, Passed 0
[error] Failed tests:
[error] example.COptionTest
[error] (Test / testOnly) sbt.TestsFailedException: Tests unsuccessful
期待通りテストは失敗した。
import ガイド
Cats は implicit を使い倒している。ライブラリを使う側としても、拡張する側としても何がどこから来てるかという一般的な勘を作っていくのは大切だ。 ただし、Cats を始めたばかりの頃はとりあえず以下の import を使ってこのページは飛ばしても大丈夫だと思う。ただし、Cats 2.2.0 以降である必要がある:
scala> import cats._, cats.data._, cats.syntax.all._
Cats 2.2.0 以前は:
scala> import cats._, cats.data._, cats.implicits._
implicit のまとめ
Scala 2 の import と implicit を手早く復習しよう! Scala では import は 2つの目的で使われる:
- 値や型の名前をスコープに取り込むため。
- implicit をスコープに取り込むため。
ある型 A があるとき、implicit はコンパイラにその型に対応する項値をもらうための機構だ。これは色々な目的で使うことができるが、Cats では主に 2つの用法がある:
- instances; 型クラスインスタンスを提供するため。
- syntax; メソッドや演算子を注入するため。(メソッド拡張)
implicit は以下の優先順位で選択される:
- プレフィックス無しでアクセスできる暗黙の値や変換子。ローカル宣言、import、外のスコープ、継承、および現在のパッケージオブジェクトから取り込まれる。同名の暗黙の値があった場合は内側のスコープのものが外側のものを shadow する。
- 暗黙のスコープ。型、その部分、および親型のコンパニオンオブジェクトおよびパッケージオブジェクト内で宣言された暗黙の値や変換子。
import cats._
まずは import cats._ で何が import されるのかみてみよう。
まずは、名前だ。Show[A] や Functor[F[_]] のような型クラスは trait として実装されていて、cats パッケージ内で定義されている。だから、cats.Show[[A] と書くかわりに Show[A] と書ける。
次も、名前だけど、これは型エイリアス。cats のパッケージオブジェクトは Eq[A] や ~>[F[_], G[_]] のような主な型エイリアスを宣言する。これも cats.Eq[A] というふうにアクセスすることができる。
最後に、Id[A] の Traverse[F[_]] や Monad[F[_]] その他への型クラスインスタンスとして catsInstancesForId が定義されているけど、気にしなくてもいい。パッケージオブジェクトに入っているというだけで暗黙のスコープに入るので、これは import しても結果は変わらない。確かめてみよう:
scala> cats.Functor[cats.Id]
res0: cats.Functor[cats.Id] = cats.package$$anon$1@3c201c09
import は必要なしということで、うまくいった。つまり、import cats._ の効果はあくまで便宜のためであって、省略可能だ。
暗黙のスコープ
2020年の3月に Travis Brown さんの #3043 がマージされて Cats 2.2.0 としてリリースされた。まとめると、この変更は標準ライブラリ型のための型クラスインスタンスを型クラスのコンパニオン・オブジェクトへと追加した。
これによって構文スコープへと import する必要性が下がり、簡潔さとコンパイラへの負荷の低下という利点がある。例えば、Cat 2.4.x 系を使った場合、以下は一切 import 無しで動作する:
scala> cats.Functor[Option]
val res1: cats.Functor[Option] = cats.instances.OptionInstances$$anon$1@56a2a3bf
詳細は Travis さんの Implicit scope and Cats を参照。
import cats.data._
次に import cats.data._ で何が取り込まれるか見ていく。
まずは、これも名前だ。cats.data パッケージ以下には Validated[+E, +A] のようなカスタムデータ型が定義されている。
次に、型エイリアス。cats.data のパッケージオブジェクト内には Reader[A, B] (ReaderT モナド変換子を特殊化したものという扱い) のような型エイリアスが定義してある。
import cats.implicits._
だとすると、import cats.implicits._ は一体何をやっているんだろう? 以下が implicits オブジェクトの定義だ:
package cats
object implicits extends syntax.AllSyntax with instances.AllInstances
これは import をまとめるのに便利な方法だ。implicits object そのものは何も定義せずに、trait をミックスインしている。以下にそれぞれの trait を詳しくみていくけど、飲茶スタイルでそれぞれ別々に import することもできる。フルコースに戻ろう。
cats.instances.AllInstances
これまでの所、僕は意図的に型クラスインスタンスという概念とメソッド注入 (別名 enrich my library) という概念をあたかも同じ事のように扱ってきた。だけど、(Int, +) が Monoid を形成することと、Monoid が |+| 演算子を導入することは 2つの異なる事柄だ。
Cats の設計方針で興味深いことの 1つとしてこれらの概念が徹底して “instance” (インスタンス) と “syntax” (構文) として区別されていることが挙げられる。たとえどれだけ一部のユーザにとって論理的に筋が通ったとしても、ライブラリがシンボルを使った演算子を導入すると議論の火種となる。 sbt、dispatch、specs などのライブラリやツールはそれぞれ独自の DSL を導入し、それらの効用に関して何度も議論が繰り広げられた。
AllInstances は、Either[A, B] や Option[A] といった標準のデータ型に対する型クラスのインスタンスのミックスインだ。
package cats
package instances
trait AllInstances
extends FunctionInstances
with StringInstances
with EitherInstances
with ListInstances
with OptionInstances
with SetInstances
with StreamInstances
with VectorInstances
with AnyValInstances
with MapInstances
with BigIntInstances
with BigDecimalInstances
with FutureInstances
with TryInstances
with TupleInstances
with UUIDInstances
with SymbolInstances
cats.syntax.AllSyntax
AllSyntax は、Cats 内にある全ての演算子をミックスインする trait だ。
package cats
package syntax
trait AllSyntax
extends ApplicativeSyntax
with ApplicativeErrorSyntax
with ApplySyntax
with BifunctorSyntax
with BifoldableSyntax
with BitraverseSyntax
with CartesianSyntax
with CoflatMapSyntax
with ComonadSyntax
with ComposeSyntax
with ContravariantSyntax
with CoproductSyntax
with EitherSyntax
with EqSyntax
....
アラカルト形式
僕は、飲茶スタイルという名前の方がいいと思うけど、カートで点心が運ばれてきて好きなものを選んで取る「飲茶」でピンと来なければ、カウンターに座って好きなものを頼む焼き鳥屋だと考えてもいい。
もし何らかの理由で cats.implicits._ を全て import したくなければ、好きなものを選ぶことができる。
型クラスインスタンス
前述の通り、Cats 2.2.0 以降は普通は何もしなくても型クラスのインスタンスを得ることができる。
cats.Monad[Option].pure(0)
// res0: Option[Int] = Some(value = 0)
何らかの理由で Option のための全ての型クラスインスタンスを導入する方法:
{
import cats.instances.option._
cats.Monad[Option].pure(0)
}
// res1: Option[Int] = Some(value = 0)
全てのインスタンスが欲しければ、以下が全て取り込む方法だ:
{
import cats.instances.all._
cats.Monoid[Int].empty
}
// res2: Int = 0
演算子の注入を一切行なっていないので、ヘルパー関数や型クラスインスタンスに定義された関数を使う必要がある (そっちの方が好みという人もいる)。
Cats 型クラスの syntax
型クラスの syntax は型クラスごとに分かれている。以下が Eq のためのメソッドや演算子を注入する方法だ:
{
import cats.syntax.eq._
1 === 1
}
// res3: Boolean = true
Cats データ型の syntax
Writer のような Cats 独自のデータ型のための syntax も cats.syntax パッケージ以下にある:
{
import cats.syntax.writer._
1.tell
}
// res4: cats.data.package.Writer[Int, Unit] = WriterT(run = (1, ()))
標準データ型の syntax
標準データ型のための sytnax はデータ型ごとに分かれている。以下が Option のための演算子とヘルパー関数を注入する方法だ:
{
import cats.syntax.option._
1.some
}
// res5: Option[Int] = Some(value = 1)
全ての syntax
以下は全ての syntax と型クラスインスタンスを取り込む方法だ。
{
import cats.syntax.all._
import cats.instances.all._
1.some
}
// res6: Option[Int] = Some(value = 1)
これは cats.implicits._ を import するのと同じだ。
繰り返すが、これを読んで分からなかったら、まずは以下を使っていれば大丈夫だ:
scala> import cats._, cats.data._, cats.syntax.all._
3日目
昨日は simulacrum を使って独自の型クラスを定義することから始めて、 Discipline を用いて Functor則を検査するところまでみた。
型を司るもの、カインド
型とは、値について何らかの推論をするために付いている小さなラベルです。そして、型にも小さなラベルが付いているんです。その名は種類 (kind)。 … 種類とはそもそも何者で、何の役に立つのでしょう?さっそく GHCi の
:kコマンドを使って、型の種類を調べてみましょう。
Scala 2.10 時点では Scala REPL に :k コマンドが無かったので、ひとつ書いてみた: kind.scala。
George Leontiev 氏 (@folone) その他のお陰で、Scala 2.11 より :kind コマンドは標準機能として取り込まれた。使ってみよう:
scala> :k Int
scala.Int's kind is A
scala> :k -v Int
scala.Int's kind is A
*
This is a proper type.
Int と他の全ての値を作ることのできる型はプロパーな型と呼ばれ * というシンボルで表記される (「型」と読む)。これは値レベルだと 1 に相当する。Scala の型変数構文を用いるとこれは A と書ける。
scala> :k -v Option
scala.Option's kind is F[+A]
* -(+)-> *
This is a type constructor: a 1st-order-kinded type.
scala> :k -v Either
scala.util.Either's kind is F[+A1,+A2]
* -(+)-> * -(+)-> *
This is a type constructor: a 1st-order-kinded type.
これらは、型コンストラクタと呼ばれる。別の見方をすると、これらはプロパーな型から1ステップ離れている型だと考えることもできる。
これは値レベルだと、1階値、つまり普通関数と呼ばれる (_: Int) + 3 などに相当する。
カリー化した表記法を用いて * -> * や * -> * -> * などと書く。このとき Option[Int] は * で、Option が * -> * であることに注意。Scala の型変数構文を用いるとこれらは F[+A]、 F[+A1,+A2] となる。
scala> :k -v Eq
algebra.Eq's kind is F[A]
* -> *
This is a type constructor: a 1st-order-kinded type.
Scala は型クラスという概念を型コンストラクタを用いてエンコード (悪く言うとコンプレクト) する。
これを見たとき、Eq は A (つまりプロパーな型) の型クラスだと思ってほしい。
Eq には Int などを渡すので、これは理にかなっている。
scala> :k -v Functor
cats.Functor's kind is X[F[A]]
(* -> *) -> *
This is a type constructor that takes type constructor(s): a higher-kinded type.
繰り返すが、Scala は型クラスを型コンストラクタを用いてエンコードするため、
これを見たとき、Functor は F[A] (つまり、型コンストラクタ) のための型クラスだと思ってほしい。
Functor には List などを渡すので、これも理にかなっている。
別の言い方をすると、これは型コンストラクタを受け取る型コンストラクタだ。
これは値レベルだと高階関数に相当するもので、高カインド型 (higher-kinded type) と呼ばれる。
これらは (* -> *) -> * と表記される。Scala の型変数構文を用いるとこれは X[F[A]] と書ける。
forms-a vs is-a
型クラス関連の用語は混用されやすい。
例えば、(Int, +) のペアはモノイドという型クラスを形成する。
口語的には、「なんらかの演算に関して X はモノイドを形成できるか? (can X form a monoid under some operation?)
という意味で「is X a monoid?」と言ったりする。
この例は、昨日の説明で、暗に Either[A, B] はファンクターである (“is-a”) という説明になっていたはずだ。
実用的では無いかもしれないが、左バイアスのかかったファンクターを定義することは可能であるため、これは正確ではないと言える。
Semigroupal
Functors, Applicative Functors and Monoids:
ここまではファンクター値を写すために、もっぱら 1 引数関数を使ってきました。では、2 引数関数でファンクターを写すと何が起こるでしょう?
import cats._
{
val hs = Functor[List].map(List(1, 2, 3, 4)) ({(_: Int) * (_:Int)}.curried)
Functor[List].map(hs) {_(9)}
}
// res0: List[Int] = List(9, 18, 27, 36)
LYAHFGG:
では、ファンクター値
Just (3 *)とファンクター値Just 5があったとして、Just (3 *)から関数を取り出してJust 5の中身に適用したくなったとしたらどうしましょう?
Control.Applicativeモジュールにある型クラスApplicativeに会いに行きましょう!型クラスApplicativeは、2つの関数pureと<*>を定義しています。
Cats はこれを Cartesian、Apply、 Applicative に分けている。以下が Cartesian のコントラクト:
/**
* [[Semigroupal]] captures the idea of composing independent effectful values.
* It is of particular interest when taken together with [[Functor]] - where [[Functor]]
* captures the idea of applying a unary pure function to an effectful value,
* calling `product` with `map` allows one to apply a function of arbitrary arity to multiple
* independent effectful values.
*
* That same idea is also manifested in the form of [[Apply]], and indeed [[Apply]] extends both
* [[Semigroupal]] and [[Functor]] to illustrate this.
*/
@typeclass trait Semigroupal[F[_]] {
def product[A, B](fa: F[A], fb: F[B]): F[(A, B)]
}
Semigroupal は product 関数を定義して、これは F[A] と F[B] から、効果 F[_] に包まれたペア (A, B) を作る。
Cartesian 則
Cartesian には結合則という法則が1つのみある:
trait CartesianLaws[F[_]] {
implicit def F: Cartesian[F]
def cartesianAssociativity[A, B, C](fa: F[A], fb: F[B], fc: F[C]): (F[(A, (B, C))], F[((A, B), C)]) =
(F.product(fa, F.product(fb, fc)), F.product(F.product(fa, fb), fc))
}
Apply
Functors, Applicative Functors and Monoids:
ここまではファンクター値を写すために、もっぱら 1 引数関数を使ってきました。では、2 引数関数でファンクターを写すと何が起こるでしょう?
import cats._, cats.syntax.all._
{
val hs = Functor[List].map(List(1, 2, 3, 4)) ({(_: Int) * (_:Int)}.curried)
Functor[List].map(hs) {_(9)}
}
// res0: List[Int] = List(9, 18, 27, 36)
LYAHFGG:
では、ファンクター値
Just (3 *)とファンクター値Just 5があったとして、Just (3 *)から関数を取り出してJust 5の中身に適用したくなったとしたらどうしましょう?
Control.Applicativeモジュールにある型クラスApplicativeに会いに行きましょう!型クラスApplicativeは、2つの関数pureと<*>を定義しています。
Cats は Applicative を Apply と Applicative に分けている。以下が Apply のコントラクト:
/**
* Weaker version of Applicative[F]; has apply but not pure.
*
* Must obey the laws defined in cats.laws.ApplyLaws.
*/
@typeclass(excludeParents = List("ApplyArityFunctions"))
trait Apply[F[_]] extends Functor[F] with Cartesian[F] with ApplyArityFunctions[F] { self =>
/**
* Given a value and a function in the Apply context, applies the
* function to the value.
*/
def ap[A, B](ff: F[A => B])(fa: F[A]): F[B]
....
}
Apply は Functor、Cartesian、そして ApplyArityFunctions を拡張することに注目してほしい。
<*> 関数は、Cats の Apply では ap と呼ばれる。(これは最初は apply と呼ばれていたが、ap に直された。+1)
LYAHFGG:
<*>はfmapの強化版なのです。fmapが普通の関数とファンクター値を引数に取って、関数をファンクター値の中の値に適用してくれるのに対し、<*>は関数の入っているファンクター値と値の入っているファンクター値を引数に取って、1つ目のファンクターの中身である関数を2つ目のファンクターの中身に適用するのです。
Applicative Style
LYAHFGG:
Applicative型クラスでは、<*>を連続して使うことができ、 1つだけでなく、複数のアプリカティブ値を組み合わせて使うことができます。
以下は Haskell で書かれた例:
ghci> pure (-) <*> Just 3 <*> Just 5
Just (-2)
Cats には apply 構文というものがある。
(3.some, 5.some) mapN { _ - _ }
// res1: Option[Int] = Some(value = -2)
(none[Int], 5.some) mapN { _ - _ }
// res2: Option[Int] = None
(3.some, none[Int]) mapN { _ - _ }
// res3: Option[Int] = None
これは Option から Cartesian が形成可能であることを示す。
Apply としての List
LYAHFGG:
リスト(正確に言えばリスト型のコンストラクタ
[])もアプリカティブファンクターです。意外ですか?
apply 構文で書けるかためしてみよう:
(List("ha", "heh", "hmm"), List("?", "!", ".")) mapN {_ + _}
// res4: List[String] = List(
// "ha?",
// "ha!",
// "ha.",
// "heh?",
// "heh!",
// "heh.",
// "hmm?",
// "hmm!",
// "hmm."
// )
*> と <* 演算子
Apply は <* と *> という 2つの演算子を可能とし、これらも Apply[F].map2 の特殊形だと考えることができる。
定義はシンプルに見えるけども、面白い効果がある:
1.some <* 2.some
// res5: Option[Int] = Some(value = 1)
none[Int] <* 2.some
// res6: Option[Int] = None
1.some *> 2.some
// res7: Option[Int] = Some(value = 2)
none[Int] *> 2.some
// res8: Option[Int] = None
どちらか一方が失敗すると、None が返ってくる。
Option syntax
次にへ行く前に、Optiona 値を作るために Cats が導入する syntax をみてみる。
9.some
// res9: Option[Int] = Some(value = 9)
none[Int]
// res10: Option[Int] = None
これで (Some(9): Option[Int]) を 9.some と書ける。
Apply としての Option
これを Apply[Option].ap と一緒に使ってみる:
import cats._, cats.syntax.all._
Apply[Option].ap({{(_: Int) + 3}.some })(9.some)
// res12: Option[Int] = Some(value = 12)
Apply[Option].ap({{(_: Int) + 3}.some })(10.some)
// res13: Option[Int] = Some(value = 13)
Apply[Option].ap({{(_: String) + "hahah"}.some })(none[String])
// res14: Option[String] = None
Apply[Option].ap({ none[String => String] })("woot".some)
// res15: Option[String] = None
どちらかが失敗すると、None が返ってくる。
昨日の simulacrum を用いた独自型クラスの定義で見たとおり、 simulacrum は型クラス・コントラクト内で定義された関数を演算子として (魔法の力で) 転写する。
({(_: Int) + 3}.some) ap 9.some
// res16: Option[Int] = Some(value = 12)
({(_: Int) + 3}.some) ap 10.some
// res17: Option[Int] = Some(value = 13)
({(_: String) + "hahah"}.some) ap none[String]
// res18: Option[String] = None
(none[String => String]) ap "woot".some
// res19: Option[String] = None
Apply の便利な関数
LYAHFGG:
Control.ApplicativeにはliftA2という、以下のような型を持つ関数があります。
liftA2 :: (Applicative f) => (a -> b -> c) -> f a -> f b -> f c .
Scala ではパラメータが逆順であることを覚えているだろうか。
つまり、F[B] と F[A] を受け取った後、(A, B) => C という関数を受け取る関数だ。
これは Apply では map2 と呼ばれている。
@typeclass(excludeParents = List("ApplyArityFunctions"))
trait Apply[F[_]] extends Functor[F] with Cartesian[F] with ApplyArityFunctions[F] { self =>
def ap[A, B](ff: F[A => B])(fa: F[A]): F[B]
def productR[A, B](fa: F[A])(fb: F[B]): F[B] =
map2(fa, fb)((_, b) => b)
def productL[A, B](fa: F[A])(fb: F[B]): F[A] =
map2(fa, fb)((a, _) => a)
override def product[A, B](fa: F[A], fb: F[B]): F[(A, B)] =
ap(map(fa)(a => (b: B) => (a, b)))(fb)
/** Alias for [[ap]]. */
@inline final def <*>[A, B](ff: F[A => B])(fa: F[A]): F[B] =
ap(ff)(fa)
/** Alias for [[productR]]. */
@inline final def *>[A, B](fa: F[A])(fb: F[B]): F[B] =
productR(fa)(fb)
/** Alias for [[productL]]. */
@inline final def <*[A, B](fa: F[A])(fb: F[B]): F[A] =
productL(fa)(fb)
/**
* ap2 is a binary version of ap, defined in terms of ap.
*/
def ap2[A, B, Z](ff: F[(A, B) => Z])(fa: F[A], fb: F[B]): F[Z] =
map(product(fa, product(fb, ff))) { case (a, (b, f)) => f(a, b) }
def map2[A, B, Z](fa: F[A], fb: F[B])(f: (A, B) => Z): F[Z] =
map(product(fa, fb))(f.tupled)
def map2Eval[A, B, Z](fa: F[A], fb: Eval[F[B]])(f: (A, B) => Z): Eval[F[Z]] =
fb.map(fb => map2(fa, fb)(f))
....
}
2項演算子に関しては、map2 を使うことでアプリカティブ・スタイルを隠蔽することができる。
同じものを 2通りの方法で書いて比較してみる:
(3.some, List(4).some) mapN { _ :: _ }
// res20: Option[List[Int]] = Some(value = List(3, 4))
Apply[Option].map2(3.some, List(4).some) { _ :: _ }
// res21: Option[List[Int]] = Some(value = List(3, 4))
同じ結果となった。
Apply[F].ap の 2パラメータ版は Apply[F].ap2 と呼ばれる:
Apply[Option].ap2({{ (_: Int) :: (_: List[Int]) }.some })(3.some, List(4).some)
// res22: Option[List[Int]] = Some(value = List(3, 4))
map2 の特殊形で tuple2 というものもあって、このように使う:
Apply[Option].tuple2(1.some, 2.some)
// res23: Option[(Int, Int)] = Some(value = (1, 2))
Apply[Option].tuple2(1.some, none[Int])
// res24: Option[(Int, Int)] = None
2つ以上のパラメータを受け取る関数があったときはどうなるんだろうかと気になっている人は、
Apply[F[_]] が ApplyArityFunctions[F] を拡張することに気付いただろうか。
これは ap3、map3、tuple3 … から始まって
ap22、map22、tuple22 まで自動生成されたコードだ。
Apply則
Apply には合成則という法則のみが1つある:
trait ApplyLaws[F[_]] extends FunctorLaws[F] {
implicit override def F: Apply[F]
def applyComposition[A, B, C](fa: F[A], fab: F[A => B], fbc: F[B => C]): IsEq[F[C]] = {
val compose: (B => C) => (A => B) => (A => C) = _.compose
fa.ap(fab).ap(fbc) <-> fa.ap(fab.ap(fbc.map(compose)))
}
}
Applicative
注意: アプリカティブ・ファンクターに興味があってこのページに飛んできた人は、まずは Semigroupal と Apply を読んでほしい。
Functors, Applicative Functors and Monoids:
Control.Applicativeモジュールにある型クラスApplicativeに会いに行きましょう!型クラスApplicativeは、2つの関数pureと<*>を定義しています。
Cats の Applicative を見てみよう:
@typeclass trait Applicative[F[_]] extends Apply[F] { self =>
/**
* `pure` lifts any value into the Applicative Functor
*
* Applicative[Option].pure(10) = Some(10)
*/
def pure[A](x: A): F[A]
....
}
Apply を拡張して pure をつけただけだ。
LYAHFGG:
pureは任意の型の引数を受け取り、それをアプリカティブ値の中に入れて返します。 … アプリカティブ値は「箱」というよりも「文脈」と考えるほうが正確かもしれません。pureは、値を引数に取り、その値を何らかのデフォルトの文脈(元の値を再現できるような最小限の文脈)に置くのです。
A の値を受け取り F[A] を返すコンストラクタみたいだ。
import cats._, cats.syntax.all._
Applicative[List].pure(1)
// res0: List[Int] = List(1)
Applicative[Option].pure(1)
// res1: Option[Int] = Some(value = 1)
これは、Apply[F].ap を書くときに {{...}.some} としなくて済むのが便利かも。
{
val F = Applicative[Option]
F.ap({ F.pure((_: Int) + 3) })(F.pure(9))
}
// res2: Option[Int] = Some(value = 12)
Option を抽象化したコードになった。
Applicative の便利な関数
LYAHFGG:
では、「アプリカティブ値のリスト」を取って「リストを返り値として持つ1つのアプリカティブ値」を返す関数を実装してみましょう。これを
sequenceAと呼ぶことにします。
sequenceA :: (Applicative f) => [f a] -> f [a]
sequenceA [] = pure []
sequenceA (x:xs) = (:) <$> x <*> sequenceA xs
これを Cats でも実装できるか試してみよう!
def sequenceA[F[_]: Applicative, A](list: List[F[A]]): F[List[A]] = list match {
case Nil => Applicative[F].pure(Nil: List[A])
case x :: xs => (x, sequenceA(xs)) mapN {_ :: _}
}
テストしてみよう:
sequenceA(List(1.some, 2.some))
// res3: Option[List[Int]] = Some(value = List(1, 2))
sequenceA(List(3.some, none[Int], 1.some))
// res4: Option[List[Int]] = None
sequenceA(List(List(1, 2, 3), List(4, 5, 6)))
// res5: List[List[Int]] = List(
// List(1, 4),
// List(1, 5),
// List(1, 6),
// List(2, 4),
// List(2, 5),
// List(2, 6),
// List(3, 4),
// List(3, 5),
// List(3, 6)
// )
正しい答えが得られた。興味深いのは結局 Applicative が必要になったことと、
sequenceA が型クラスを利用したジェネリックな形になっていることだ。
sequenceAは、関数のリストがあり、そのすべてに同じ引数を食わして結果をリストとして眺めたい、という場合にはとても便利です。
Function1 の片側が Int に固定された例は、型解釈を付ける必要がある。
{
val f = sequenceA[Function1[Int, *], Int](List((_: Int) + 3, (_: Int) + 2, (_: Int) + 1))
f(3)
}
// res6: List[Int] = List(6, 5, 4)
Applicative則
以下がの Applicative のための法則だ:
- identity:
pure id <*> v = v - homomorphism:
pure f <*> pure x = pure (f x) - interchange:
u <*> pure y = pure ($ y) <*> u
Cats はもう 1つ別の法則を定義している:
def applicativeMap[A, B](fa: F[A], f: A => B): IsEq[F[B]] =
fa.map(f) <-> fa.ap(F.pure(f))
F.ap と F.pure を合成したとき、それは F.map と同じ効果を得られるということみたいだ。
結構長くなったけど、ここまでたどり着けて良かったと思う。続きはまたあとで。
4日目
昨日はカインドと型をおさらいして、Apply と
applicative style を探索した後で、
sequenceA にたどり着いた。
続いて今日は Semigroup と Monoid をやってみよう。
Semigroup
「すごいHaskellたのしく学ぼう」の本を持ってるひとは新しい章に進める。モノイドだ。ウェブサイトを読んでるひとは Functors, Applicative Functors and Monoids の続きだ。
とりあえず、Cats には newtype や tagged type 的な機能は入ってないみたいだ。
後で自分たちで実装することにする。
Haskell の Monoid は、Cats では Semigroup と Monoid に分かれている。
これらはそれぞれ algebra.Semigroup と algebra.Monoid の型エイリアスだ。
Apply と Applicative 同様に、Semigroup は Monoid の弱いバージョンだ。
同じ問題を解く事ができるなら、より少ない前提を置くため弱い方がかっこいい。
LYAHFGG:
LYAHFGG:
例えば、
(3 * 4) * 5も3 * (4 * 5)も、答は60です。++についてもこの性質は成り立ちます。 …この性質を結合的 (associativity) と呼びます。演算
*と++は結合的であると言います。結合的でない演算の例は-です。
確かめてみる:
import cats._, cats.syntax.all._
assert { (3 * 2) * (8 * 5) === 3 * (2 * (8 * 5)) }
assert { List("la") ++ (List("di") ++ List("da")) === (List("la") ++ List("di")) ++ List("da") }
エラーがないから等価ということだ。
Semigroup 型クラス
これが algebra.Semigroup の型クラスコントラクトだ。
/**
* A semigroup is any set `A` with an associative operation (`combine`).
*/
trait Semigroup[@sp(Int, Long, Float, Double) A] extends Any with Serializable {
/**
* Associative operation taking which combines two values.
*/
def combine(x: A, y: A): A
....
}
これは combine 演算子とそのシンボルを使ったエイリアスである |+| を可能とする。使ってみる。
List(1, 2, 3) |+| List(4, 5, 6)
// res2: List[Int] = List(1, 2, 3, 4, 5, 6)
"one" |+| "two"
// res3: String = "onetwo"
Semigroup則
結合則が semigroup の唯一の法則だ。
- associativity
(x |+| y) |+| z = x |+| (y |+| z)
以下は、Semigroup則を REPL から検査する方法だ。 詳細はDiscipline を用いた法則のチェックを参照。
scala> import cats._, cats.data._, cats.implicits._
import cats._
import cats.data._
import cats.implicits._
scala> import cats.kernel.laws.GroupLaws
import cats.kernel.laws.GroupLaws
scala> val rs1 = GroupLaws[Int].semigroup(Semigroup[Int])
rs1: cats.kernel.laws.GroupLaws[Int]#GroupProperties = cats.kernel.laws.GroupLaws$GroupProperties@5a077d1d
scala> rs1.all.check
+ semigroup.associativity: OK, passed 100 tests.
+ semigroup.combineN(a, 1) == a: OK, passed 100 tests.
+ semigroup.combineN(a, 2) == a |+| a: OK, passed 100 tests.
+ semigroup.serializable: OK, proved property.
Semigroups としての List
List(1, 2, 3) |+| List(4, 5, 6)
// res4: List[Int] = List(1, 2, 3, 4, 5, 6)
積と和
Int は、+ と * の両方に関して semigroup を形成することができる。
Tagged type の代わりに、cats は加算に対してにのみ
semigroup のインスタンスを提供するという方法をとっている。
これを演算子構文で書くのはトリッキーだ。
def doSomething[A: Semigroup](a1: A, a2: A): A =
a1 |+| a2
doSomething(3, 5)(Semigroup[Int])
// res5: Int = 8
これなら、関数構文で書いたほうが楽かもしれない:
Semigroup[Int].combine(3, 5)
// res6: Int = 8
Monoid
LYAHFGG:
どうやら、
*に1という組み合わせと、++に[]という組み合わせは、共通の性質を持っているようですね。
- 関数は引数を2つ取る。
- 2つの引数および返り値の型はすべて等しい。
- 2引数関数を施して相手を変えないような特殊な値が存在する。
これを Scala で確かめてみる:
4 * 1
// res0: Int = 4
1 * 9
// res1: Int = 9
List(1, 2, 3) ++ Nil
// res2: List[Int] = List(1, 2, 3)
Nil ++ List(0.5, 2.5)
// res3: List[Double] = List(0.5, 2.5)
あってるみたいだ。
Monoid 型クラス
以下が algebera.Monoid の型クラス・コントラクトだ:
/**
* A monoid is a semigroup with an identity. A monoid is a specialization of a
* semigroup, so its operation must be associative. Additionally,
* `combine(x, empty) == combine(empty, x) == x`. For example, if we have `Monoid[String]`,
* with `combine` as string concatenation, then `empty = ""`.
*/
trait Monoid[@sp(Int, Long, Float, Double) A] extends Any with Semigroup[A] {
/**
* Return the identity element for this monoid.
*/
def empty: A
...
}
Monoid則
Semigroup則に加えて、Monoid則はもう 2つの法則がある:
- associativity
(x |+| y) |+| z = x |+| (y |+| z) - left identity
Monoid[A].empty |+| x = x - right identity
x |+| Monoid[A].empty = x
REPL から Monoid則を検査してみよう:
scala> import cats._, cats.syntax.all._
import cats._
import cats.syntax.all._
scala> import cats.kernel.laws.discipline.MonoidTests
import cats.kernel.laws.discipline.MonoidTests
scala> import org.scalacheck.Test.Parameters
import org.scalacheck.Test.Parameters
scala> val rs1 = MonoidTests[Int].monoid
val rs1: cats.kernel.laws.discipline.MonoidTests[Int]#RuleSet = org.typelevel.discipline.Laws$DefaultRuleSet@108684fb
scala> rs1.all.check(Parameters.default)
+ monoid.associative: OK, passed 100 tests.
+ monoid.collect0: OK, passed 100 tests.
+ monoid.combine all: OK, passed 100 tests.
+ monoid.combineAllOption: OK, passed 100 tests.
+ monoid.intercalateCombineAllOption: OK, passed 100 tests.
+ monoid.intercalateIntercalates: OK, passed 100 tests.
+ monoid.intercalateRepeat1: OK, passed 100 tests.
+ monoid.intercalateRepeat2: OK, passed 100 tests.
+ monoid.is id: OK, passed 100 tests.
+ monoid.left identity: OK, passed 100 tests.
+ monoid.repeat0: OK, passed 100 tests.
+ monoid.repeat1: OK, passed 100 tests.
+ monoid.repeat2: OK, passed 100 tests.
+ monoid.reverseCombineAllOption: OK, passed 100 tests.
+ monoid.reverseRepeat1: OK, passed 100 tests.
+ monoid.reverseRepeat2: OK, passed 100 tests.
+ monoid.reverseReverses: OK, passed 100 tests.
+ monoid.right identity: OK, passed 100 tests.
MUnit test で書くとこうなる:
package example
import cats._
import cats.kernel.laws.discipline.MonoidTests
class IntTest extends munit.DisciplineSuite {
checkAll("Int", MonoidTests[Int].monoid)
}
値クラス
LYAHFGG:
Haskell の newtype キーワードは、まさにこのような「1つの型を取り、それを何かにくるんで別の型に見せかけたい」という場合のために作られたものです。
Cats は tagged type 的な機能を持たないけども、現在の Scala には値クラスがある。ある一定の条件下ではこれは unboxed (メモリ割り当てオーバーヘッドが無いこと) を保つので、簡単な例に使う分には問題無いと思う。
class Wrapper(val unwrap: Int) extends AnyVal
Disjunction と Conjunction
LYAHFGG:
モノイドにする方法が2通りあって、どちらも捨てがたいような型は、
Num a以外にもあります。Boolです。1つ目の方法は||をモノイド演算とし、Falseを単位元とする方法です。 ….
BoolをMonoidのインスタンスにするもう1つの方法は、Anyのいわば真逆です。&&をモノイド演算とし、Trueを単位元とする方法です。
Cats はこれを提供しないけども、自分で実装してみる。
import cats._, cats.syntax.all._
// `class Disjunction(val unwrap: Boolean) extends AnyVal` doesn't work on mdoc
class Disjunction(val unwrap: Boolean)
object Disjunction {
@inline def apply(b: Boolean): Disjunction = new Disjunction(b)
implicit val disjunctionMonoid: Monoid[Disjunction] = new Monoid[Disjunction] {
def combine(a1: Disjunction, a2: Disjunction): Disjunction =
Disjunction(a1.unwrap || a2.unwrap)
def empty: Disjunction = Disjunction(false)
}
implicit val disjunctionEq: Eq[Disjunction] = new Eq[Disjunction] {
def eqv(a1: Disjunction, a2: Disjunction): Boolean =
a1.unwrap == a2.unwrap
}
}
val x1 = Disjunction(true) |+| Disjunction(false)
// x1: Disjunction = repl.MdocSessionDisjunction@67bf7df7
x1.unwrap
// res4: Boolean = true
val x2 = Monoid[Disjunction].empty |+| Disjunction(true)
// x2: Disjunction = repl.MdocSessionDisjunction@78016f6f
x2.unwrap
// res5: Boolean = true
こっちが Conjunction:
// `class Conjunction(val unwrap: Boolean) extends AnyVal` doesn't work on mdoc
class Conjunction(val unwrap: Boolean)
object Conjunction {
@inline def apply(b: Boolean): Conjunction = new Conjunction(b)
implicit val conjunctionMonoid: Monoid[Conjunction] = new Monoid[Conjunction] {
def combine(a1: Conjunction, a2: Conjunction): Conjunction =
Conjunction(a1.unwrap && a2.unwrap)
def empty: Conjunction = Conjunction(true)
}
implicit val conjunctionEq: Eq[Conjunction] = new Eq[Conjunction] {
def eqv(a1: Conjunction, a2: Conjunction): Boolean =
a1.unwrap == a2.unwrap
}
}
val x3 = Conjunction(true) |+| Conjunction(false)
// x3: Conjunction = repl.MdocSessionConjunction@40b73a81
x3.unwrap
// res6: Boolean = false
val x4 = Monoid[Conjunction].empty |+| Conjunction(true)
// x4: Conjunction = repl.MdocSessionConjunction@c708b1e
x4.unwrap
// res7: Boolean = true
独自 newtype がちゃんと Monoid則を満たしているかチェックするべきだ。
scala> import cats._, cats.syntax.all._
import cats._
import cats.syntax.all._
scala> import cats.kernel.laws.discipline.MonoidTests
import cats.kernel.laws.discipline.MonoidTests
scala> import org.scalacheck.Test.Parameters
import org.scalacheck.Test.Parameters
scala> import org.scalacheck.{ Arbitrary, Gen }
import org.scalacheck.{Arbitrary, Gen}
scala> implicit def arbDisjunction(implicit ev: Arbitrary[Boolean]): Arbitrary[Disjunction] =
Arbitrary { ev.arbitrary map { Disjunction(_) } }
def arbDisjunction(implicit ev: org.scalacheck.Arbitrary[Boolean]): org.scalacheck.Arbitrary[Disjunction]
scala> val rs1 = MonoidTests[Disjunction].monoid
val rs1: cats.kernel.laws.discipline.MonoidTests[Disjunction]#RuleSet = org.typelevel.discipline.Laws$DefaultRuleSet@464d134
scala> rs1.all.check(Parameters.default)
+ monoid.associative: OK, passed 100 tests.
+ monoid.collect0: OK, passed 100 tests.
+ monoid.combine all: OK, passed 100 tests.
+ monoid.combineAllOption: OK, passed 100 tests.
....
Disjunction は動いた。
scala> implicit def arbConjunction(implicit ev: Arbitrary[Boolean]): Arbitrary[Conjunction] =
Arbitrary { ev.arbitrary map { Conjunction(_) } }
def arbConjunction(implicit ev: org.scalacheck.Arbitrary[Boolean]): org.scalacheck.Arbitrary[Conjunction]
scala> val rs2 = MonoidTests[Conjunction].monoid
val rs2: cats.kernel.laws.discipline.MonoidTests[Conjunction]#RuleSet = org.typelevel.discipline.Laws$DefaultRuleSet@71a4f643
scala> rs2.all.check(Parameters.default)
+ monoid.associative: OK, passed 100 tests.
+ monoid.collect0: OK, passed 100 tests.
+ monoid.combine all: OK, passed 100 tests.
+ monoid.combineAllOption: OK, passed 100 tests.
....
Conjunction も大丈夫そうだ。
Monoid としての Option
LYAHFGG:
Maybe aをモノイドにする1つ目の方法は、型引数aがモノイドであるときに限りMaybe aもモノイドであるとし、Maybe aのmappendを、Justの中身のmappendを使って定義することです。
Cats がこうなっているか確認しよう。
implicit def optionMonoid[A](implicit ev: Semigroup[A]): Monoid[Option[A]] =
new Monoid[Option[A]] {
def empty: Option[A] = None
def combine(x: Option[A], y: Option[A]): Option[A] =
x match {
case None => y
case Some(xx) => y match {
case None => x
case Some(yy) => Some(ev.combine(xx,yy))
}
}
}
mappend を combine と読み替えれば、あとはパターンマッチだけだ。
使ってみよう。
none[String] |+| "andy".some
// res8: Option[String] = Some(value = "andy")
1.some |+| none[Int]
// res9: Option[Int] = Some(value = 1)
ちゃんと動く。
LYAHFGG:
中身がモノイドがどうか分からない状態では、
mappendは使えません。どうすればいいでしょう? 1つの選択は、第一引数を返して第二引数は捨てる、と決めておくことです。この用途のためにFirst aというものが存在します。
Haskell は newtype を使って First 型コンストラクタを実装している。
ジェネリックな値クラスの場合はメモリ割り当てを回避することができないので、普通に case class を使おう。
case class First[A: Eq](val unwrap: Option[A])
object First {
implicit def firstMonoid[A: Eq]: Monoid[First[A]] = new Monoid[First[A]] {
def combine(a1: First[A], a2: First[A]): First[A] =
First((a1.unwrap, a2.unwrap) match {
case (Some(x), _) => Some(x)
case (None, y) => y
})
def empty: First[A] = First(None: Option[A])
}
implicit def firstEq[A: Eq]: Eq[First[A]] = new Eq[First[A]] {
def eqv(a1: First[A], a2: First[A]): Boolean =
Eq[Option[A]].eqv(a1.unwrap, a2.unwrap)
}
}
First('a'.some) |+| First('b'.some)
// res10: First[Char] = First(unwrap = Some(value = 'a'))
First(none[Char]) |+| First('b'.some)
// res11: First[Char] = First(unwrap = Some(value = 'b'))
Monoid則を検査:
scala> implicit def arbFirst[A: Eq](implicit ev: Arbitrary[Option[A]]): Arbitrary[First[A]] =
Arbitrary { ev.arbitrary map { First(_) } }
def arbFirst[A](implicit evidence$1: cats.Eq[A], ev: org.scalacheck.Arbitrary[Option[A]]): org.scalacheck.Arbitrary[First[A]]
scala> val rs3 = MonoidTests[First[Int]].monoid
val rs3: cats.kernel.laws.discipline.MonoidTests[First[Int]]#RuleSet = org.typelevel.discipline.Laws$DefaultRuleSet@17d3711d
scala> rs3.all.check(Parameters.default)
+ monoid.associative: OK, passed 100 tests.
+ monoid.collect0: OK, passed 100 tests.
+ monoid.combine all: OK, passed 100 tests.
+ monoid.combineAllOption: OK, passed 100 tests.
....
First もシリアライズできないらしい。
LYAHFGG:
逆に、2つの
Justをmappendしたときに後のほうの引数を優先するようなMaybe aが欲しい、という人のために、Data.MonoidにはLast a型も用意されています。
case class Last[A: Eq](val unwrap: Option[A])
object Last {
implicit def lastMonoid[A: Eq]: Monoid[Last[A]] = new Monoid[Last[A]] {
def combine(a1: Last[A], a2: Last[A]): Last[A] =
Last((a1.unwrap, a2.unwrap) match {
case (_, Some(y)) => Some(y)
case (x, None) => x
})
def empty: Last[A] = Last(None: Option[A])
}
implicit def lastEq[A: Eq]: Eq[Last[A]] = new Eq[Last[A]] {
def eqv(a1: Last[A], a2: Last[A]): Boolean =
Eq[Option[A]].eqv(a1.unwrap, a2.unwrap)
}
}
Last('a'.some) |+| Last('b'.some)
// res12: Last[Char] = Last(unwrap = Some(value = 'b'))
Last('a'.some) |+| Last(none[Char])
// res13: Last[Char] = Last(unwrap = Some(value = 'a'))
また、法則検査。
scala> implicit def arbLast[A: Eq](implicit ev: Arbitrary[Option[A]]): Arbitrary[Last[A]] =
Arbitrary { ev.arbitrary map { Last(_) } }
def arbLast[A](implicit evidence$1: cats.Eq[A], ev: org.scalacheck.Arbitrary[Option[A]]): org.scalacheck.Arbitrary[Last[A]]
scala> val rs4 = MonoidTests[Last[Int]].monoid
val rs4: cats.kernel.laws.discipline.MonoidTests[Last[Int]]#RuleSet = org.typelevel.discipline.Laws$DefaultRuleSet@7b28ea53
scala> rs4.all.check(Parameters.default)
+ monoid.associative: OK, passed 100 tests.
+ monoid.collect0: OK, passed 100 tests.
+ monoid.combine all: OK, passed 100 tests.
+ monoid.combineAllOption: OK, passed 100 tests.
....
モノイドが何なのか感じがつかめて気がする。
法則に関して
今日は法則に関して色々やった。何故法則なんているんだろうか?
法則は重要だから法則は重要である、はトートロジーだけども、 1かけらの真実も含まれている。例えば、ある土地の中ではある特定の側を車が走ることを規定した道路交通法のように、全員が従えばそれだけで便利な法則もある。
Cats や Haskell スタイルの関数型プログラミングが可能とするのは、
データ、コンテナ、実行モデルなどを抽象化させたコードを書くことだ。
この抽象化は法則で言明されたことのみを前提とするため、
抽象的なコードが正しく動作するためには全ての A: Monoid が法則を満たしている必要がある。
これを実利主義的視点と呼べる。
何らかの実利があることを受け入れたとしても、何故これら特定の法則なのかは気になる。
HaskellWiki や SPJ論文の一つに書いてあるからに決まってる。
これらを既存の実装付きの取っ掛かりとして、真似をすることができる。
これは伝統主義的視点と呼べる。
ただ、これは Hakell 特有の設計方針や制限まで受け継いでしまう危険をはらんでいる。
例えば、圏論における函手 (functor) は Functor[F] よりも広い意味を持つ用語だ。fmap は F[A] => F[B] を返す関数なので関連性がある。
Scala の map まで来ると、型推論のせいでその関係すら消えてしまう。
最終的には、僕たちの理解を数学までつなげるべきだ。 Monoid則はモノイドの数学的な定義に対応し、そこから既知のモノイドの特性の恩恵を得ることができる。 特にこれは Monoid則に関連することで、3つの法則は圏の3公理と同じもので、それはモノイドは圏の特殊形であることに由来する。
習う過程では、カーゴ・カルトから始めるのも悪くないと思う。 模倣とパターン認識を通して僕達は言語を習得してきたはずだ。
モノイドを使ったデータ構造の畳み込み
LYAHFGG:
畳み込み相性の良いデータ構造は実にたくさんあるので、
Foldable型クラスが導入されました。Functorが関数で写せるものを表すように、Foldableは畳み込みできるものを表しています。
Cats でこれに対応するものも Foldable と呼ばれている。型クラスのコントラクトも見てみよう:
/**
* Data structures that can be folded to a summary value.
*
* In the case of a collection (such as `List` or `Set`), these
* methods will fold together (combine) the values contained in the
* collection to produce a single result. Most collection types have
* `foldLeft` methods, which will usually be used by the associationed
* `Fold[_]` instance.
*
* Foldable[F] is implemented in terms of two basic methods:
*
* - `foldLeft(fa, b)(f)` eagerly folds `fa` from left-to-right.
* - `foldLazy(fa, b)(f)` lazily folds `fa` from right-to-left.
*
* Beyond these it provides many other useful methods related to
* folding over F[A] values.
*
* See: [[https://www.cs.nott.ac.uk/~gmh/fold.pdf A tutorial on the universality and expressiveness of fold]]
*/
@typeclass trait Foldable[F[_]] extends Serializable { self =>
/**
* Left associative fold on 'F' using the function 'f'.
*/
def foldLeft[A, B](fa: F[A], b: B)(f: (B, A) => B): B
/**
* Right associative lazy fold on `F` using the folding function 'f'.
*
* This method evaluates `b` lazily (in some cases it will not be
* needed), and returns a lazy value. We are using `A => Fold[B]` to
* support laziness in a stack-safe way.
*
* For more detailed information about how this method works see the
* documentation for `Fold[_]`.
*/
def foldLazy[A, B](fa: F[A], lb: Lazy[B])(f: A => Fold[B]): Lazy[B] =
Lazy(partialFold[A, B](fa)(f).complete(lb))
/**
* Low-level method that powers `foldLazy`.
*/
def partialFold[A, B](fa: F[A])(f: A => Fold[B]): Fold[B]
....
}
このように使う:
import cats._, cats.syntax.all._
Foldable[List].foldLeft(List(1, 2, 3), 1) {_ * _}
// res0: Int = 6
Foldable はいくつかの便利な関数や演算子がついてきて、型クラスを駆使している。
まずは fold。Monoid[A] が empty と combine を提供するので、これだけで畳込みをすることができる。
/**
* Fold implemented using the given Monoid[A] instance.
*/
def fold[A](fa: F[A])(implicit A: Monoid[A]): A =
foldLeft(fa, A.empty) { (acc, a) =>
A.combine(acc, a)
}
使ってみる。
Foldable[List].fold(List(1, 2, 3))(Monoid[Int])
// res1: Int = 6
関数を受け取る変種として foldMap もある。
/**
* Fold implemented by mapping `A` values into `B` and then
* combining them using the given `Monoid[B]` instance.
*/
def foldMap[A, B](fa: F[A])(f: A => B)(implicit B: Monoid[B]): B =
foldLeft(fa, B.empty) { (b, a) =>
B.combine(b, f(a))
}
標準のコレクションライブラリが foldMap を実装しないため、演算子として使える。
List(1, 2, 3).foldMap(identity)(Monoid[Int])
// res2: Int = 6
もう一つ便利なのは、これで値を newtype に変換することができることだ。
// `class Conjunction(val unwrap: Boolean) extends AnyVal` doesn't work on mdoc
class Conjunction(val unwrap: Boolean)
object Conjunction {
@inline def apply(b: Boolean): Conjunction = new Conjunction(b)
implicit val conjunctionMonoid: Monoid[Conjunction] = new Monoid[Conjunction] {
def combine(a1: Conjunction, a2: Conjunction): Conjunction =
Conjunction(a1.unwrap && a2.unwrap)
def empty: Conjunction = Conjunction(true)
}
implicit val conjunctionEq: Eq[Conjunction] = new Eq[Conjunction] {
def eqv(a1: Conjunction, a2: Conjunction): Boolean =
a1.unwrap == a2.unwrap
}
}
val x = List(true, false, true) foldMap {Conjunction(_)}
// x: Conjunction = repl.MdocSessionConjunction@5d64621e
x.unwrap
// res3: Boolean = false
Conjunction(true) と一つ一つ書きだして |+| でつなぐよりずっと楽だ。
続きはまた後で。
5日目

4日目は Semigroup と Monoid をみて、
独自のモノイドを実装した。あとは、foldMap などができる Foldable も少しかじった。
Apply.ap
今日は、更新のお知らせから。まず、3日目にみた Apply.apply だけど、
Apply.ap に改名された (戻ったとも言えるが)。 #308
Serializable な型クラスインスタンス
以前のバージョンでモノイドの法則検査を値クラスに対して行った時に Serializable
関連で失敗していた。
これは、実は Cats のせいじゃないらしいことが分かった。Cats の
gitter に行った所、Erik (@d6/@non)
が親切に僕の型クラスインスタンスが serializable じゃないのは
REPL から定義されているせいだと教えてもらった。
First を src/ 以下で定義した所、法則は普通に合格した。
Jason Zaugg (@retronym) さんの指摘によると、分散処理時に受送信両者の Cats のバージョンが完全に一致するとき以外でのシリアライゼーションをサポートするには、さらに:
- 匿名クラスの回避 (クラス名の変更を避けるため)
- 全てに
@SerialVersionUID(0L)を付ける必要がある
など他にも気をつけることがあるということだった。
FlatMap
今日はすごいHaskellたのしく学ぼうの新しい章「モナドがいっぱい」を始めることができる。
モナドはある願いを叶えるための、アプリカティブ値の自然な拡張です。その願いとは、「普通の値
aを取って文脈付きの値を返す関数に、文脈付きの値m aを渡したい」というものです。
Cats は Monad 型クラスを FlatMap と Monad という 2つの型クラスに分ける。
以下が[FlatMap の型クラスのコントラクト]だ:
@typeclass trait FlatMap[F[_]] extends Apply[F] {
def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B]
def tailRecM[A, B](a: A)(f: A => F[Either[A, B]]): F[B]
....
}
FlatMap が、Applicative の弱いバージョンである Apply を拡張することに注目してほしい。これらが演算子だ:
class FlatMapOps[F[_], A](fa: F[A])(implicit F: FlatMap[F]) {
def flatMap[B](f: A => F[B]): F[B] = F.flatMap(fa)(f)
def mproduct[B](f: A => F[B]): F[(A, B)] = F.mproduct(fa)(f)
def >>=[B](f: A => F[B]): F[B] = F.flatMap(fa)(f)
def >>[B](fb: F[B]): F[B] = F.flatMap(fa)(_ => fb)
}
これは flatMap 演算子とシンボルを使ったエイリアスである >>= を導入する。他の演算子に関しては後回しにしよう。とりあえず標準ライブラリで flatMap は慣れている:
import cats._, cats.syntax.all._
(Right(3): Either[String, Int]) flatMap { x => Right(x + 1) }
// res0: Either[String, Int] = Right(value = 4)
Option から始める
本の通り、Option から始めよう。この節では Cats の型クラスを使っているのか標準ライブラリの実装なのかについてはうるさく言わないことにする。
以下がファンクターとしての Option:
"wisdom".some map { _ + "!" }
// res1: Option[String] = Some(value = "wisdom!")
none[String] map { _ + "!" }
// res2: Option[String] = None
Apply としての Option:
({(_: Int) + 3}.some) ap 3.some
// res3: Option[Int] = Some(value = 6)
none[String => String] ap "greed".some
// res4: Option[String] = None
({(_: String).toInt}.some) ap none[String]
// res5: Option[Int] = None
以下は FlatMap としての Option:
3.some flatMap { (x: Int) => (x + 1).some }
// res6: Option[Int] = Some(value = 4)
"smile".some flatMap { (x: String) => (x + " :)").some }
// res7: Option[String] = Some(value = "smile :)")
none[Int] flatMap { (x: Int) => (x + 1).some }
// res8: Option[Int] = None
none[String] flatMap { (x: String) => (x + " :)").some }
// res9: Option[String] = None
期待通り、モナディックな値が None の場合は None が返ってきた。
FlatMap則
FlatMap には結合律 (associativity) という法則がある:
- associativity:
(m flatMap f) flatMap g === m flatMap { x => f(x) flatMap {g} }
Cats の FlatMapLaws にはあと 2つ定義してある:
trait FlatMapLaws[F[_]] extends ApplyLaws[F] {
implicit override def F: FlatMap[F]
def flatMapAssociativity[A, B, C](fa: F[A], f: A => F[B], g: B => F[C]): IsEq[F[C]] =
fa.flatMap(f).flatMap(g) <-> fa.flatMap(a => f(a).flatMap(g))
def flatMapConsistentApply[A, B](fa: F[A], fab: F[A => B]): IsEq[F[B]] =
fab.ap(fa) <-> fab.flatMap(f => fa.map(f))
/**
* The composition of `cats.data.Kleisli` arrows is associative. This is
* analogous to [[flatMapAssociativity]].
*/
def kleisliAssociativity[A, B, C, D](f: A => F[B], g: B => F[C], h: C => F[D], a: A): IsEq[F[D]] = {
val (kf, kg, kh) = (Kleisli(f), Kleisli(g), Kleisli(h))
((kf andThen kg) andThen kh).run(a) <-> (kf andThen (kg andThen kh)).run(a)
}
}
Monad
先ほど Cats はモナド型クラスを FlatMap と Monad の2つに分けると書いた。
この FlatMap-Monad の関係は、Apply-Applicative の関係の相似となっている:
@typeclass trait Monad[F[_]] extends FlatMap[F] with Applicative[F] {
....
}
Monad は FlatMap に pure を付けたものだ。Haskell と違って Monad[F] は Applicative[F] を拡張するため、return と pure と名前が異なるという問題が生じていない。
綱渡り

LYAHFGG:
さて、棒の左右にとまった鳥の数の差が3以内であれば、ピエールはバランスを取れているものとしましょう。例えば、右に1羽、左に4羽の鳥がとまっているなら大丈夫。だけど左に5羽目の鳥がとまったら、ピエールはバランスを崩して飛び降りる羽目になります。
本の Pole の例題を実装してみよう。
import cats._, cats.syntax.all._
type Birds = Int
case class Pole(left: Birds, right: Birds)
Scala ではこんな風に Int に型エイリアスを付けるのは一般的じゃないと思うけど、ものは試しだ。landLeft と landRight をメソッドをとして実装したいから Pole は case class にする:
case class Pole(left: Birds, right: Birds) {
def landLeft(n: Birds): Pole = copy(left = left + n)
def landRight(n: Birds): Pole = copy(right = right + n)
}
OO の方が見栄えが良いと思う:
Pole(0, 0).landLeft(2)
// res1: Pole = Pole(left = 2, right = 0)
Pole(1, 2).landRight(1)
// res2: Pole = Pole(left = 1, right = 3)
Pole(1, 2).landRight(-1)
// res3: Pole = Pole(left = 1, right = 1)
連鎖も可能:
Pole(0, 0).landLeft(1).landRight(1).landLeft(2)
// res4: Pole = Pole(left = 3, right = 1)
Pole(0, 0).landLeft(1).landRight(4).landLeft(-1).landRight(-2)
// res5: Pole = Pole(left = 0, right = 2)
本が言うとおり、中間値で失敗しても計算が続行してしまっている。失敗を Option[Pole] で表現しよう:
case class Pole(left: Birds, right: Birds) {
def landLeft(n: Birds): Option[Pole] =
if (math.abs((left + n) - right) < 4) copy(left = left + n).some
else none[Pole]
def landRight(n: Birds): Option[Pole] =
if (math.abs(left - (right + n)) < 4) copy(right = right + n).some
else none[Pole]
}
Pole(0, 0).landLeft(2)
// res7: Option[Pole] = Some(value = Pole(left = 2, right = 0))
Pole(0, 3).landLeft(10)
// res8: Option[Pole] = None
flatMap もしくはシンボル使ったエイリアスである >>= を使って landLeft と landRight をチェインする:
val rlr = Monad[Option].pure(Pole(0, 0)) >>= {_.landRight(2)} >>=
{_.landLeft(2)} >>= {_.landRight(2)}
// rlr: Option[Pole] = Some(value = Pole(left = 2, right = 4))
モナディックチェインが綱渡りのシミュレーションを改善したか確かめる:
val lrlr = Monad[Option].pure(Pole(0, 0)) >>= {_.landLeft(1)} >>=
{_.landRight(4)} >>= {_.landLeft(-1)} >>= {_.landRight(-2)}
// lrlr: Option[Pole] = None
うまくいった。この例はモナドが何なのかをうまく体現しているので、じっくり考えて理解してほしい。
- まず、
pureがPole(0, 0)をデフォルトのコンテクストで包む:Pole(0, 0).some - 次に、
Pole(0, 0).some >>= {_.landLeft(1)}が起こる。これはSome値なので、Pole(0, 0)に_.landLeft(1)が適用されて、Pole(1, 0).someが返ってくる。 - 次に、
Pole(1, 0).some >>= {_.landRight(4)}が起こる。結果はPole(1, 4).some。これでバランス棒の左右の差の最大値となった。 Pole(1, 4).some >>= {_.landLeft(-1)}が発生して、none[Pole]が返ってくる。差が大きすぎて、バランスが崩れてしまった。none[Pole] >>= {_.landRight(-2)}は自動的にnone[Pole]となる。
モナディックな関数をチェインでは、一つの関数の効果 (effect) が次々と渡されていくのが見えると思う。
ロープの上のバナナ
LYAHFGG:
さて、今度はバランス棒にとまっている鳥の数によらず、いきなりピエールを滑らせて落っことす関数を作ってみましょう。この関数を
bananaと呼ぶことにします。
以下が常に失敗する banana だ:
case class Pole(left: Birds, right: Birds) {
def landLeft(n: Birds): Option[Pole] =
if (math.abs((left + n) - right) < 4) copy(left = left + n).some
else none[Pole]
def landRight(n: Birds): Option[Pole] =
if (math.abs(left - (right + n)) < 4) copy(right = right + n).some
else none[Pole]
def banana: Option[Pole] = none[Pole]
}
val lbl = Monad[Option].pure(Pole(0, 0)) >>= {_.landLeft(1)} >>=
{_.banana} >>= {_.landRight(1)}
// lbl: Option[Pole] = None
LYAHFGG:
ところで、入力に関係なく既定のモナド値を返す関数だったら、自作せずとも
>>関数を使うという手があります。
以下が >> の Option での振る舞い:
none[Int] >> 3.some
// res10: Option[Int] = None
3.some >> 4.some
// res11: Option[Int] = Some(value = 4)
3.some >> none[Int]
// res12: Option[Int] = None
banana を >> none[Pole] に置き換えてみよう:
{
val lbl = Monad[Option].pure(Pole(0, 0)) >>= {_.landLeft(1)} >>
none[Pole] >>= {_.landRight(1)}
}
// error: Option[Int] does not take parameters
// 3.some >> none[Int]
// ^
突然型推論が崩れてしまった。問題の原因はおそらく演算子の優先順位にある。 Programming in Scala 曰く:
The one exception to the precedence rule, alluded to above, concerns assignment operators, which end in an equals character. If an operator ends in an equals character (
=), and the operator is not one of the comparison operators<=,>=,==, or!=, then the precedence of the operator is the same as that of simple assignment (=). That is, it is lower than the precedence of any other operator.
注意: 上記の記述は不完全だ。代入演算子ルールのもう1つの例外は演算子が === のように (=) から始まる場合だ。
>>= (bind) が等号で終わるため、優先順位は最下位に落とされ、({_.landLeft(1)} >> (none: Option[Pole])) が先に評価される。いくつかの気が進まない回避方法がある。まず、普通のメソッド呼び出しのようにドットと括弧の記法を使うことができる:
Monad[Option].pure(Pole(0, 0)).>>=({_.landLeft(1)}).>>(none[Pole]).>>=({_.landRight(1)})
// res14: Option[Pole] = None
もしくは優先順位の問題に気付いたなら、適切な場所に括弧を置くことができる:
(Monad[Option].pure(Pole(0, 0)) >>= {_.landLeft(1)}) >> none[Pole] >>= {_.landRight(1)}
// res15: Option[Pole] = None
両方とも正しい答が得られた。
for 内包表記
LYAHFGG:
Haskell にとってモナドはとても便利なので、モナド専用構文まで用意されています。その名は
do記法。
まずは入れ子のラムダ式を書いてみよう:
3.some >>= { x => "!".some >>= { y => (x.show + y).some } }
// res16: Option[String] = Some(value = "3!")
>>= が使われたことで計算のどの部分も失敗することができる:
3.some >>= { x => none[String] >>= { y => (x.show + y).some } }
// res17: Option[String] = None
(none: Option[Int]) >>= { x => "!".some >>= { y => (x.show + y).some } }
// res18: Option[String] = None
3.some >>= { x => "!".some >>= { y => none[String] } }
// res19: Option[String] = None
Haskell の do 記法のかわりに、Scala には for 内包表記があり、これらは似た機能を持つ:
for {
x <- 3.some
y <- "!".some
} yield (x.show + y)
// res20: Option[String] = Some(value = "3!")
LYAHFGG:
do式は、let行を除いてすべてモナド値で構成されます。
これは for では微妙に違うと思うけど、また今度。
帰ってきたピエール
LYAHFGG:
ピエールの綱渡りの動作も、もちろん
do記法で書けます。
def routine: Option[Pole] =
for {
start <- Monad[Option].pure(Pole(0, 0))
first <- start.landLeft(2)
second <- first.landRight(2)
third <- second.landLeft(1)
} yield third
routine
// res21: Option[Pole] = Some(value = Pole(left = 3, right = 2))
yield は Option[Pole] じゃなくて Pole を受け取るため、third も抽出する必要があった。
LYAHFGG:
ピエールにバナナの皮を踏ませたい場合、
do記法ではこう書きます。
{
def routine: Option[Pole] =
for {
start <- Monad[Option].pure(Pole(0, 0))
first <- start.landLeft(2)
_ <- none[Pole]
second <- first.landRight(2)
third <- second.landLeft(1)
} yield third
routine
}
// res22: Option[Pole] = None
パターンマッチングと失敗
LYAHFGG:
do記法でモナド値を変数名に束縛するときには、let式や関数の引数のときと同様、パターンマッチが使えます。
def justH: Option[Char] =
for {
(x :: xs) <- "hello".toList.some
} yield x
justH
// res23: Option[Char] = Some(value = 'h')
do式の中でパターンマッチが失敗した場合、Monad型クラスの一員であるfail関数が使われるので、異常終了という形ではなく、そのモナドの文脈に合った形で失敗を処理できます。
def wopwop: Option[Char] =
for {
(x :: xs) <- "".toList.some
} yield x
wopwop
// res24: Option[Char] = None
失敗したパターンマッチングは None を返している。これは for 構文の興味深い一面で、今まで考えたことがなかったが、言われるとなるほどと思う。
Monad則
モナドには 3つの法則がある:
- 左単位元 (left identity):
(Monad[F].pure(x) flatMap {f}) === f(x) - 右単位元 (right identity):
(m flatMap {Monad[F].pure(_)}) === m - 結合律 (associativity):
(m flatMap f) flatMap g === m flatMap { x => f(x) flatMap {g} }
LYAHFGG:
第一のモナド則が言っているのは、
returnを使って値をデフォルトの文脈に入れたものを>>=を使って関数に食わせた結果は、単にその値にその関数を適用した結果と等しくなりなさい、ということです。
これを Scala で表現すると、
assert { (Monad[Option].pure(3) >>= { x => (x + 100000).some }) ===
({ (x: Int) => (x + 100000).some })(3) }
LYAHFGG:
モナドの第二法則は、
>>=を使ってモナド値をreturnに食わせた結果は、元のモナド値と不変であると言っています。
assert { ("move on up".some >>= {Monad[Option].pure(_)}) === "move on up".some }
LYAHFGG:
最後のモナド則は、
>>=を使ったモナド関数適用の連鎖があるときに、どの順序で評価しても結果は同じであるべき、というものです。
Monad[Option].pure(Pole(0, 0)) >>= {_.landRight(2)} >>= {_.landLeft(2)} >>= {_.landRight(2)}
// res27: Option[Pole] = Some(value = Pole(left = 2, right = 4))
Monad[Option].pure(Pole(0, 0)) >>= { x =>
x.landRight(2) >>= { y =>
y.landLeft(2) >>= { z =>
z.landRight(2)
}}}
// res28: Option[Pole] = Some(value = Pole(left = 2, right = 4))
4日目の Monoid則を覚えていると、見覚えがあるかもしれない。 それは、モナドはモノイドの特殊な形だからだ。
「ちょっと待て。Monoid は A (別名 *) のカインドのためのものじゃないのか?」と思うかもしれない。
確かにその通り。そして、これが「モノイド」と Monoid[A] の差でもある。
Haskell スタイルの関数型プログラミングはコンテナや実行モデルを抽象化することができる。
圏論では、モノイドといった概念は A、F[A]、F[A] => F[B] といった色んなものに一般化することができる。
「オーマイガー。法則多杉」と思うよりも、多くの法則はそれらをつなぐ基盤となる構造があるということを知ってほしい。
Discipline を使った Monad則の検査はこうなる:
scala> import cats._, cats.syntax.all._, cats.laws.discipline.MonadTests
import cats._
import cats.syntax.all._
import cats.laws.discipline.MonadTests
scala> val rs = MonadTests[Option].monad[Int, Int, Int]
val rs: cats.laws.discipline.MonadTests[Option]#RuleSet = cats.laws.discipline.MonadTests$$anon$1@253d7b2b
scala> import org.scalacheck.Test.Parameters
import org.scalacheck.Test.Parameters
scala> rs.all.check(Parameters.default)
+ monad.ap consistent with product + map: OK, passed 100 tests.
+ monad.applicative homomorphism: OK, passed 100 tests.
+ monad.applicative identity: OK, passed 100 tests.
+ monad.applicative interchange: OK, passed 100 tests.
+ monad.applicative map: OK, passed 100 tests.
+ monad.applicative unit: OK, passed 100 tests.
+ monad.apply composition: OK, passed 100 tests.
+ monad.covariant composition: OK, passed 100 tests.
+ monad.covariant identity: OK, passed 100 tests.
+ monad.flatMap associativity: OK, passed 100 tests.
+ monad.flatMap consistent apply: OK, passed 100 tests.
+ monad.flatMap from tailRecM consistency: OK, passed 100 tests.
+ monad.invariant composition: OK, passed 100 tests.
+ monad.invariant identity: OK, passed 100 tests.
+ monad.map flatMap coherence: OK, passed 100 tests.
+ monad.map2/map2Eval consistency: OK, passed 100 tests.
+ monad.map2/product-map consistency: OK, passed 100 tests.
+ monad.monad left identity: OK, passed 100 tests.
+ monad.monad right identity: OK, passed 100 tests.
+ monad.monoidal left identity: OK, passed 100 tests.
+ monad.monoidal right identity: OK, passed 100 tests.
+ monad.mproduct consistent flatMap: OK, passed 100 tests.
+ monad.productL consistent map2: OK, passed 100 tests.
+ monad.productR consistent map2: OK, passed 100 tests.
+ monad.semigroupal associativity: OK, passed 100 tests.
+ monad.tailRecM consistent flatMap: OK, passed 100 tests.
+ monad.tailRecM stack safety: OK, proved property.
List データ型
LYAHFGG:
一方、
[3,8,9]のような値は複数の計算結果を含んでいるとも、複数の候補値を同時に重ね合わせたような1つの値であるとも解釈できます。リストをアプリカティブ・スタイルで使うと、非決定性を表現していることがはっきりします。
まずは Applicative としての List を復習する:
import cats._, cats.syntax.all._
(List(1, 2, 3), List(10, 100, 100)) mapN { _ * _ }
// res0: List[Int] = List(10, 100, 100, 20, 200, 200, 30, 300, 300)
それでは、非決定的値を関数に食わせてみましょう。
List(3, 4, 5) >>= { x => List(x, -x) }
// res1: List[Int] = List(3, -3, 4, -4, 5, -5)
モナディックな視点に立つと、List というコンテキストは複数の解がありうる数学的な値を表す。それ以外は、for を使って List を操作するなどは素の Scala と変わらない:
for {
n <- List(1, 2)
ch <- List('a', 'b')
} yield (n, ch)
// res2: List[(Int, Char)] = List((1, 'a'), (1, 'b'), (2, 'a'), (2, 'b'))
FunctorFilter
Scala の for 内包表記はフィルタリングができる:
// plain Scala
for {
x <- (1 to 50).toList if x.toString contains '7'
} yield x
// res0: List[Int] = List(7, 17, 27, 37, 47)
@typeclass
trait FunctorFilter[F[_]] extends Serializable {
def functor: Functor[F]
def mapFilter[A, B](fa: F[A])(f: A => Option[B]): F[B]
def collect[A, B](fa: F[A])(f: PartialFunction[A, B]): F[B] =
mapFilter(fa)(f.lift)
def flattenOption[A](fa: F[Option[A]]): F[A] =
mapFilter(fa)(identity)
def filter[A](fa: F[A])(f: A => Boolean): F[A] =
mapFilter(fa)(a => if (f(a)) Some(a) else None)
def filterNot[A](fa: F[A])(f: A => Boolean): F[A] =
mapFilter(fa)(Some(_).filterNot(f))
}
このように使うことができる:
import cats._, cats.syntax.all._
val english = Map(1 -> "one", 3 -> "three", 10 -> "ten")
// english: Map[Int, String] = Map(1 -> "one", 3 -> "three", 10 -> "ten")
(1 to 50).toList mapFilter { english.get(_) }
// res1: List[String] = List("one", "three", "ten")
def collectEnglish[F[_]: FunctorFilter](f: F[Int]): F[String] =
f collect {
case 1 => "one"
case 3 => "three"
case 10 => "ten"
}
collectEnglish((1 to 50).toList)
// res2: List[String] = List("one", "three", "ten")
def filterSeven[F[_]: FunctorFilter](f: F[Int]): F[Int] =
f filter { _.show contains '7' }
filterSeven((1 to 50).toList)
// res3: List[Int] = List(7, 17, 27, 37, 47)
騎士の旅
LYAHFGG:
ここで、非決定性計算を使って解くのにうってつけの問題をご紹介しましょう。チェス盤の上にナイトの駒が1つだけ乗っています。ナイトを3回動かして特定のマスまで移動させられるか、というのが問題です。
ペアに型エイリアスを付けるかわりにまた case class にしよう:
case class KnightPos(c: Int, r: Int)
以下がナイトの次に取りうる位置を全て計算する関数だ:
case class KnightPos(c: Int, r: Int) {
def move: List[KnightPos] =
for {
KnightPos(c2, r2) <- List(KnightPos(c + 2, r - 1), KnightPos(c + 2, r + 1),
KnightPos(c - 2, r - 1), KnightPos(c - 2, r + 1),
KnightPos(c + 1, r - 2), KnightPos(c + 1, r + 2),
KnightPos(c - 1, r - 2), KnightPos(c - 1, r + 2)) if (
((1 to 8).toList contains c2) && ((1 to 8).toList contains r2))
} yield KnightPos(c2, r2)
}
KnightPos(6, 2).move
// res1: List[KnightPos] = List(
// KnightPos(c = 8, r = 1),
// KnightPos(c = 8, r = 3),
// KnightPos(c = 4, r = 1),
// KnightPos(c = 4, r = 3),
// KnightPos(c = 7, r = 4),
// KnightPos(c = 5, r = 4)
// )
KnightPos(8, 1).move
// res2: List[KnightPos] = List(
// KnightPos(c = 6, r = 2),
// KnightPos(c = 7, r = 3)
// )
答は合ってるみたいだ。次に、3回のチェインを実装する:
case class KnightPos(c: Int, r: Int) {
def move: List[KnightPos] =
for {
KnightPos(c2, r2) <- List(KnightPos(c + 2, r - 1), KnightPos(c + 2, r + 1),
KnightPos(c - 2, r - 1), KnightPos(c - 2, r + 1),
KnightPos(c + 1, r - 2), KnightPos(c + 1, r + 2),
KnightPos(c - 1, r - 2), KnightPos(c - 1, r + 2)) if (
((1 to 8).toList contains c2) && ((1 to 8).toList contains r2))
} yield KnightPos(c2, r2)
def in3: List[KnightPos] =
for {
first <- move
second <- first.move
third <- second.move
} yield third
def canReachIn3(end: KnightPos): Boolean = in3 contains end
}
KnightPos(6, 2) canReachIn3 KnightPos(6, 1)
// res4: Boolean = true
KnightPos(6, 2) canReachIn3 KnightPos(7, 3)
// res5: Boolean = false
(6, 2) からは 3手で (6, 1) に動かすことができるけども、(7, 3) は無理のようだ。ピエールの鳥の例と同じように、モナド計算の鍵となっているのは 1手の効果が次に伝搬していることだと思う。
また、続きはここから。
6日目
昨日は、FlatMap と Monad 型クラスをみた。また、モナディックなチェインが値にコンテキストを与えることも確認した。Option も List も標準ライブラリに flatMap があるから、新しいコードというよりは今まであったものに対して視点を変えて見るという感じになった。あと、モナディックな演算をチェインする方法としての for 構文も確認した。
本題に入る前にここで使っている Scala ベースのブログ/ブックプラットフォームである Pamflet を紹介したい。 Pamflet は Nathan Hamblen (@n8han) さんが始めたプロジェクトで、僕もいくつかの機能をコントリビュートした。 そう言えば、ここのソースも eed3si9n/herding-cats で公開しているので、どうやって作ってるのかを知りたい人は見てみてほしい。 これまでの記事を全て校正して pull request をしてもらった Leif Wickland (@leifwickland) さんにもここでお礼を言いたい。
do vs for
Haskell の do 記法と Scala の for 内包表記には微妙な違いがある。以下が do 記法の例:
foo = do
x <- Just 3
y <- Just "!"
Just (show x ++ y)
通常は return (show x ++ y) と書くと思うけど、最後の行がモナディックな値であることを強調するために Just を書き出した。一方 Scala はこうだ:
def foo = for {
x <- Some(3)
y <- Some("!")
} yield x.toString + y
似ているように見えるけども、いくつかの違いがある。
- Scala には標準で
Monad型が無い。その代わりにコンパイラが機械的に for 内包表記をmap、withFilter、flatMap、foreachの呼び出しに展開する。 SLS 6.19 OptionやListなど、標準ライブラリがmap/flatMapを実装するものは、Cats が提供する型クラスよりも組み込みの実装が優先される。- Scala collection ライブラリの
mapその他はF[A]をG[B]に変換するCanBuildFromを受け取る。Scala コレクションのアーキテクチャ 参照。 CanBuildFromはG[A]からF[B]という変換を行うこともある。- pure 値を伴う
yieldを必要とする。さもないと、forはUnitを返す。
具体例を見てみよう:
import collection.immutable.BitSet
val bits = BitSet(1, 2, 3)
// bits: BitSet = BitSet(1, 2, 3)
for {
x <- bits
} yield x.toFloat
// res0: collection.immutable.SortedSet[Float] = TreeSet(1.0F, 2.0F, 3.0F)
for {
i <- List(1, 2, 3)
j <- Some(1)
} yield i + j
// res1: List[Int] = List(2, 3, 4)
for {
i <- Map(1 -> 2)
j <- Some(3)
} yield j
// res2: collection.immutable.Iterable[Int] = List(3)
actM を実装する
Scala には、マクロを使って命令型的なコードをモナディックもしくは applicative な関数呼び出しに変換している DSL がいくつか既にある:
Scala 構文の全域をマクロでカバーするのは難しい作業だけども、
Async と Effectful のコードをコピペすることで単純な式と val
のみをサポートするオモチャマクロを作ってみた。
詳細は省くが、ポイントは以下の関数だ:
def transform(group: BindGroup, isPure: Boolean): Tree =
group match {
case (binds, tree) =>
binds match {
case Nil =>
if (isPure) q"""$monadInstance.pure($tree)"""
else tree
case (name, unwrappedFrom) :: xs =>
val innerTree = transform((xs, tree), isPure)
val param = ValDef(Modifiers(Flag.PARAM), name, TypeTree(), EmptyTree)
q"""$monadInstance.flatMap($unwrappedFrom) { $param => $innerTree }"""
}
}
actM を使ってみよう:
import cats._, cats.syntax.all._
import example.MonadSyntax._
actM[Option, String] {
val x = 3.some.next
val y = "!".some.next
x.toString + y
}
// res3: Option[String] = Some(value = "3!")
fa.next は Monad[F].flatMap(fa)() の呼び出しに展開される。
そのため、上の例はこのように展開される:
Monad[Option].flatMap[String, String]({
val fa0: Option[Int] = 3.some
Monad[Option].flatMap[Int, String](fa0) { (arg0: Int) => {
val next0: Int = arg0
val x: Int = next0
val fa1: Option[String] = "!".some
Monad[Option].flatMap[String, String](fa1)((arg1: String) => {
val next1: String = arg1
val y: String = next1
Monad[Option].pure[String](x.toString + y)
})
}}
}) { (arg2: String) => Monad[Option].pure[String](arg2) }
// res4: Option[String] = Some(value = "3!")
Option から List への自動変換を防止できるか試してみる:
{
actM[List, Int] {
val i = List(1, 2, 3).next
val j = 1.some.next
i + j
}
}
// error: Option[String] does not take parameters
// Monad[Option].flatMap[String, String]({
// ^
エラーメッセージがこなれないけども、コンパイル時に検知することができた。
これは、Future を含むどのモナドでも動作する。
val x = {
import scala.concurrent.{ExecutionContext, Future}
import ExecutionContext.Implicits.global
actM[Future, Int] {
val i = Future { 1 }.next
val j = Future { 2 }.next
i + j
}
}
// x: concurrent.Future[Int] = Future(Success(3))
x.value
// res6: Option[util.Try[Int]] = None
このマクロは不完全な toy code だけども、こういうものがあれば便利なのではという示唆はできたと思う。
Writer データ型
Maybeモナドが失敗の可能性という文脈付きの値を表し、リストモナドが非決定性が付いた値を表しているのに対し、Writerモナドは、もう1つの値がくっついた値を表し、付加された値はログのように振る舞います。
本に従って applyLog 関数を実装してみよう:
def isBigGang(x: Int): (Boolean, String) =
(x > 9, "Compared gang size to 9.")
implicit class PairOps[A](pair: (A, String)) {
def applyLog[B](f: A => (B, String)): (B, String) = {
val (x, log) = pair
val (y, newlog) = f(x)
(y, log ++ newlog)
}
}
(3, "Smallish gang.") applyLog isBigGang
// res0: (Boolean, String) = (false, "Smallish gang.Compared gang size to 9.")
メソッドの注入が implicit のユースケースとしては多いため、Scala 2.10 に implicit class という糖衣構文が登場して、クラスから強化クラスに昇進させるのが簡単になった。ログを Semigroup として一般化する:
import cats._, cats.syntax.all._
implicit class PairOps[A, B: Semigroup](pair: (A, B)) {
def applyLog[C](f: A => (C, B)): (C, B) = {
val (x, log) = pair
val (y, newlog) = f(x)
(y, log |+| newlog)
}
}
Writer
LYAHFGG:
値にモノイドのおまけを付けるには、タプルに入れるだけです。
Writer w a型の実体は、そんなタプルのnewtypeラッパーにすぎず、定義はとてもシンプルです。
Cats でこれに対応するのは `Writer` だ:
type Writer[L, V] = WriterT[Id, L, V]
object Writer {
def apply[L, V](l: L, v: V): WriterT[Id, L, V] = WriterT[Id, L, V]((l, v))
def value[L:Monoid, V](v: V): Writer[L, V] = WriterT.value(v)
def tell[L](l: L): Writer[L, Unit] = WriterT.tell(l)
}
Writer[L, V] は、WriterT[Id, L, V] の型エイリアスだ。
WriterT
以下は `WriterT` を単純化したものだ:
final case class WriterT[F[_], L, V](run: F[(L, V)]) {
def tell(l: L)(implicit functorF: Functor[F], semigroupL: Semigroup[L]): WriterT[F, L, V] =
mapWritten(_ |+| l)
def written(implicit functorF: Functor[F]): F[L] =
functorF.map(run)(_._1)
def value(implicit functorF: Functor[F]): F[V] =
functorF.map(run)(_._2)
def mapBoth[M, U](f: (L, V) => (M, U))(implicit functorF: Functor[F]): WriterT[F, M, U] =
WriterT { functorF.map(run)(f.tupled) }
def mapWritten[M](f: L => M)(implicit functorF: Functor[F]): WriterT[F, M, V] =
mapBoth((l, v) => (f(l), v))
}
Writer の値はこのように作る:
import cats._, cats.data._, cats.syntax.all._
val w = Writer("Smallish gang.", 3)
// w: WriterT[Id, String, Int] = WriterT(run = ("Smallish gang.", 3))
val v = Writer.value[String, Int](3)
// v: Writer[String, Int] = WriterT(run = ("", 3))
val l = Writer.tell[String]("Log something")
// l: Writer[String, Unit] = WriterT(run = ("Log something", ()))
Writer データ型を実行するには run メソッドを呼ぶ:
w.run
// res2: (String, Int) = ("Smallish gang.", 3)
Writer に for 構文を使う
LYAHFGG:
こうして
Monadインスタンスができたので、Writerをdo記法で自由に扱えます。
def logNumber(x: Int): Writer[List[String], Int] =
Writer(List("Got number: " + x.show), 3)
def multWithLog: Writer[List[String], Int] =
for {
a <- logNumber(3)
b <- logNumber(5)
} yield a * b
multWithLog.run
// res3: (List[String], Int) = (List("Got number: 3", "Got number: 5"), 9)
プログラムにログを追加する
以下が例題の gcd だ:
def gcd(a: Int, b: Int): Writer[List[String], Int] = {
if (b == 0) for {
_ <- Writer.tell(List("Finished with " + a.show))
} yield a
else
Writer.tell(List(s"${a.show} mod ${b.show} = ${(a % b).show}")) >>= { _ =>
gcd(b, a % b)
}
}
gcd(12, 16).run
// res4: (List[String], Int) = (
// List("12 mod 16 = 12", "16 mod 12 = 4", "12 mod 4 = 0", "Finished with 4"),
// 4
// )
非効率な List の構築
LYAHFGG:
Writerモナドを使うときは、使うモナドに気をつけてください。リストを使うととても遅くなる場合があるからです。リストはmappendに++を使っていますが、++を使ってリストの最後にものを追加する操作は、そのリストがとても長いと遅くなってしまいます。
主なコレクションの性能特性をまとめた表があるので見てみよう。不変コレクションで目立っているのが全ての演算を実質定数でこなす Vector だ。Vector は分岐度が 32 の木構造で、構造共有を行うことで高速な更新を実現している。
Vector を使った gcd:
def gcd(a: Int, b: Int): Writer[Vector[String], Int] = {
if (b == 0) for {
_ <- Writer.tell(Vector("Finished with " + a.show))
} yield a
else
Writer.tell(Vector(s"${a.show} mod ${b.show} = ${(a % b).show}")) >>= { _ =>
gcd(b, a % b)
}
}
gcd(12, 16).run
// res6: (Vector[String], Int) = (
// Vector("12 mod 16 = 12", "16 mod 12 = 4", "12 mod 4 = 0", "Finished with 4"),
// 4
// )
性能の比較
本のように性能を比較するマイクロベンチマークを書いてみよう:
def vectorFinalCountDown(x: Int): Writer[Vector[String], Unit] = {
import annotation.tailrec
@tailrec def doFinalCountDown(x: Int, w: Writer[Vector[String], Unit]): Writer[Vector[String], Unit] = x match {
case 0 => w >>= { _ => Writer.tell(Vector("0")) }
case x => doFinalCountDown(x - 1, w >>= { _ =>
Writer.tell(Vector(x.show))
})
}
val t0 = System.currentTimeMillis
val r = doFinalCountDown(x, Writer.tell(Vector[String]()))
val t1 = System.currentTimeMillis
r >>= { _ => Writer.tell(Vector((t1 - t0).show + " msec")) }
}
def listFinalCountDown(x: Int): Writer[List[String], Unit] = {
import annotation.tailrec
@tailrec def doFinalCountDown(x: Int, w: Writer[List[String], Unit]): Writer[List[String], Unit] = x match {
case 0 => w >>= { _ => Writer.tell(List("0")) }
case x => doFinalCountDown(x - 1, w >>= { _ =>
Writer.tell(List(x.show))
})
}
val t0 = System.currentTimeMillis
val r = doFinalCountDown(x, Writer.tell(List[String]()))
val t1 = System.currentTimeMillis
r >>= { _ => Writer.tell(List((t1 - t0).show + " msec")) }
}
僕のマシンの実行結果だとこうなった:
scala> vectorFinalCountDown(10000).run._1.last
res17: String = 6 msec
scala> listFinalCountDown(10000).run._1.last
res18: String = 630 msec
List が 100倍遅いことが分かる。
Reader データ型
第11章では、関数を作る型、
(->) rも、Functorのインスタンスであることを見ました。
import cats._, cats.syntax.all._
val f = (_: Int) * 2
// f: Int => Int = <function1>
val g = (_: Int) + 10
// g: Int => Int = <function1>
(g map f)(8)
// res0: Int = 36
それから、関数はアプリカティブファンクターであることも見ましたね。これにより、関数が将来返すであろう値を、すでに持っているかのように演算できるようになりました。
{
val h = (f, g) mapN {_ + _}
h(3)
}
// res1: Int = 19
関数の型
(->) rはファンクターであり、アプリカティブファンクターであるばかりでなく、モナドでもあります。これまでに登場したモナド値と同様、関数もまた文脈を持った値だとみなすことができるのです。関数にとっての文脈とは、値がまだ手元になく、値が欲しければその関数を別の何かに適用しないといけない、というものです。
この例題も実装してみよう:
{
val addStuff: Int => Int = for {
a <- (_: Int) * 2
b <- (_: Int) + 10
} yield a + b
addStuff(3)
}
// res2: Int = 19
(*2)と(+10)はどちらも3に適用されます。実は、return (a+b)も同じく3に適用されるんですが、引数を無視して常にa+bを返しています。そいういうわけで、関数モナドは Reader モナドとも呼ばれたりします。すべての関数が共通の情報を「読む」からです。
Reader モナドは値が既にあるかのようなフリをさせてくれる。恐らくこれは1つのパラメータを受け取る関数でしか使えない。
DI: Dependency injection
2012年3月9日にあった nescala 2012 で Rúnar (@runarorama) さんが
Dead-Simple Dependency Injection
というトークを行った。そこで提示されたアイディアの一つは Reader モナドを dependency injection
に使うというものだった。同年の 12月に YOW 2012 でそのトークを長くした
Lambda: The Ultimate Dependency Injection Framework
も行われた。
翌 2013年に Jason Arhart さんが書いた
Scrap Your Cake Pattern Boilerplate: Dependency Injection Using the Reader Monad
に基づいた例をここでは使うことにする。
まず、ユーザを表す case class と、ユーザを取得するためのデータストアを抽象化した trait があるとする。
case class User(id: Long, parentId: Long, name: String, email: String)
trait UserRepo {
def get(id: Long): User
def find(name: String): User
}
次に、UserRepo trait の全ての演算に対してプリミティブ・リーダーを定義する:
trait Users {
def getUser(id: Long): UserRepo => User = {
case repo => repo.get(id)
}
def findUser(name: String): UserRepo => User = {
case repo => repo.find(name)
}
}
(ボイラープレートをぶち壊せとか言いつつ) これはボイラープレートっぽい。一応、次。
プリミティブ・リーダーを合成することで、アプリケーションを含む他のリーダーを作ることができる。
object UserInfo extends Users {
def userInfo(name: String): UserRepo => Map[String, String] =
for {
user <- findUser(name)
boss <- getUser(user.parentId)
} yield Map(
"name" -> s"${user.name}",
"email" -> s"${user.email}",
"boss_name" -> s"${boss.name}"
)
}
trait Program {
def app: UserRepo => String =
for {
fredo <- UserInfo.userInfo("Fredo")
} yield fredo.toString
}
この app を実行するためには、UserRepo の実装を提供する何かが必要だ:
val testUsers = List(User(0, 0, "Vito", "vito@example.com"),
User(1, 0, "Michael", "michael@example.com"),
User(2, 0, "Fredo", "fredo@example.com"))
// testUsers: List[User] = List(
// User(id = 0L, parentId = 0L, name = "Vito", email = "vito@example.com"),
// User(id = 1L, parentId = 0L, name = "Michael", email = "michael@example.com"),
// User(id = 2L, parentId = 0L, name = "Fredo", email = "fredo@example.com")
// )
object Main extends Program {
def run: String = app(mkUserRepo)
def mkUserRepo: UserRepo = new UserRepo {
def get(id: Long): User = (testUsers find { _.id === id }).get
def find(name: String): User = (testUsers find { _.name === name }).get
}
}
Main.run
// res3: String = "Map(name -> Fredo, email -> fredo@example.com, boss_name -> Vito)"
ボスの名前が表示された。
for 内包表記の代わりに actM を使ってみる:
object UserInfo extends Users {
import example.MonadSyntax._
def userInfo(name: String): UserRepo => Map[String, String] =
actM[UserRepo => *, Map[String, String]] {
val user = findUser(name).next
val boss = getUser(user.parentId).next
Map(
"name" -> s"${user.name}",
"email" -> s"${user.email}",
"boss_name" -> s"${boss.name}"
)
}
}
trait Program {
import example.MonadSyntax._
def app: UserRepo => String =
actM[UserRepo => *, String] {
val fredo = UserInfo.userInfo("Fredo").next
fredo.toString
}
}
object Main extends Program {
def run: String = app(mkUserRepo)
def mkUserRepo: UserRepo = new UserRepo {
def get(id: Long): User = (testUsers find { _.id === id }).get
def find(name: String): User = (testUsers find { _.name === name }).get
}
}
Main.run
// res5: String = "Map(name -> Fredo, email -> fredo@example.com, boss_name -> Vito)"
actM ブロックの中は for バージョンよりも自然な形に見えるけども、
型注釈が必要なせいで、多分こっちの方が使いづらいと思う。
今日はここまで。
7日目
6日目は、for 内包表記と do 記法を比較して、actM マクロを実装した。
また、Function1[A, B] を別の視点からとらえた Reader データ型に関してもみた。
ここの所、言葉遣いがいいかげんになって List や Reader
を「モナド」と呼んできたが、これからは正確に List データ型、
Reader データ型と呼んでいきたい。
そして、それらのデータ型が、何らかの演算に関してモナドを形成する。
State データ型
不変 (immutable) なデータ構造を使ってコードを書いていると、
何らかの状態を表す値を引き回すというパターンがよく発生する。
僕が好きな例はテトリスだ。テトリスの関数型の実装があるとして、
Tetrix.init が初期状態を作って、他に色々な状態遷移関数が変換された状態と何らかの戻り値を返すとする:
val (s0, _) = Tetrix.init()
val (s1, _) = Tetrix.nextBlock(s0)
val (s2, moved0) = Tetrix.moveBlock(s1, LEFT)
val (s3, moved1) =
if (moved0) Tetrix.moveBlock(s2, LEFT)
else (s2, moved0)
状態オブジェクト (s0, s1, s2, …) の引き回しはエラーの温床的なボイラープレートとなる。
状態の明示的な引き回しを自動化するのがゴールだ。
本にあわせてここではスタックの例を使う。まずは、State 無しでの実装:
import cats._, cats.syntax.all._
type Stack = List[Int]
def pop(s0: Stack): (Stack, Int) =
s0 match {
case x :: xs => (xs, x)
case Nil => sys.error("stack is empty")
}
def push(s0: Stack, a: Int): (Stack, Unit) = (a :: s0, ())
def stackManip(s0: Stack): (Stack, Int) = {
val (s1, _) = push(s0, 3)
val (s2, a) = pop(s1)
pop(s2)
}
stackManip(List(5, 8, 2, 1))
// res0: (Stack, Int) = (List(8, 2, 1), 5)
State と StateT データ型
そこで Haskell には
Stateモナドが用意されています。これさえあれば、状態付きの計算などいとも簡単。しかもすべてを純粋に保ったまま扱えるんです。…状態付きの計算とは、ある状態を取って、更新された状態と一緒に計算結果を返す関数として表現できるでしょう。そんな関数の型は、こうなるはずです。
s -> (a, s)
State は状態付きの計算 S => (S, A) をカプセル化するデータ型だ。
State は型 S で表される状態を渡すモナドを形成する。
Haskell はこの混乱を避けるために、Stater とか Program という名前を付けるべきだったと思うけど、
既に State という名前が定着してるので、もう遅いだろう。
Cody Allen (@ceedubs) さんが Cats に
State/StateT を実装する #302 を投げていて、それが最近マージされた。(Erik サンキュー)
State はただの型エイリアスとなっている:
package object data {
....
type State[S, A] = StateT[Eval, S, A]
object State extends StateFunctions
}
StateT はモナド変換子で、これは他のデータ型を受け取る型コンストラクタだ。
State はこれに Trampoline 部分適用している。
Eval は in-memory でコール・スタックをエミュレートしてスタックオーバーフローを回避するための機構だ。
以下が StateT の定義:
final class StateT[F[_], S, A](val runF: F[S => F[(S, A)]]) {
....
}
object StateT extends StateTInstances {
def apply[F[_], S, A](f: S => F[(S, A)])(implicit F: Applicative[F]): StateT[F, S, A] =
new StateT(F.pure(f))
def applyF[F[_], S, A](runF: F[S => F[(S, A)]]): StateT[F, S, A] =
new StateT(runF)
/**
* Run with the provided initial state value
*/
def run(initial: S)(implicit F: FlatMap[F]): F[(S, A)] =
F.flatMap(runF)(f => f(initial))
....
}
State 値を構築するには、状態遷移関数を State.apply に渡す:
private[data] abstract class StateFunctions {
def apply[S, A](f: S => (S, A)): State[S, A] =
StateT.applyF(Now((s: S) => Now(f(s))))
....
}
State の実装はできたてなので、まだ小慣れない部分もあったりする。
REPL から State を使ってみると、最初の state は成功するけど、2つ目が失敗するという奇妙な動作に遭遇した。
@retronym に
SI-7139: Type alias and object with the same name cause type mismatch in REPL
のことを教えてもらって、#322 として回避することができた。
State を使ってスタックを実装してみよう:
type Stack = List[Int]
import cats._, cats.data._, cats.syntax.all._
val pop = State[Stack, Int] {
case x :: xs => (xs, x)
case Nil => sys.error("stack is empty")
}
// pop: State[Stack, Int] = cats.data.IndexedStateT@18e63d38
def push(a: Int) = State[Stack, Unit] {
case xs => (a :: xs, ())
}
これらがプリミティブ・プログラムだ。 これらをモナド的に合成することで複合プログラムを構築することができる。
def stackManip: State[Stack, Int] = for {
_ <- push(3)
a <- pop
b <- pop
} yield(b)
stackManip.run(List(5, 8, 2, 1)).value
// res2: (Stack, Int) = (List(8, 2, 1), 5)
最初の run は SateT のためで、2つ目の run は Eval を最後まで実行する。
push も pop も純粋関数型だけども、状態オブジェクト (s0, s1, …)
の引き回しをしなくても済むようになった。
状態の取得と設定
LYAHFGG:
Control.Monad.Stateモジュールは、2つの便利な関数getとputを備えた、MonadStateという型クラスを提供しています。
State object は、いくつかのヘルパー関数を定義する:
private[data] abstract class StateFunctions {
def apply[S, A](f: S => (S, A)): State[S, A] =
StateT.applyF(Now((s: S) => Now(f(s))))
/**
* Return `a` and maintain the input state.
*/
def pure[S, A](a: A): State[S, A] = State(s => (s, a))
/**
* Modify the input state and return Unit.
*/
def modify[S](f: S => S): State[S, Unit] = State(s => (f(s), ()))
/**
* Inspect a value from the input state, without modifying the state.
*/
def inspect[S, T](f: S => T): State[S, T] = State(s => (s, f(s)))
/**
* Return the input state without modifying it.
*/
def get[S]: State[S, S] = inspect(identity)
/**
* Set the state to `s` and return Unit.
*/
def set[S](s: S): State[S, Unit] = State(_ => (s, ()))
}
ちょっと最初は分かりづらかった。だけど、State モナドは状態遷移関数と戻り値をカプセル化していることを思い出してほしい。
そのため、状態というコンテキストでの State.get は、状態はそのままにして、状態を戻り値として返すというものだ。
似たように、状態というコンテキストでの State.set(s) は、状態を s で上書きして、戻り値として () を返す。
本で出てくる stackStack 関数を実装して具体例でみてみよう。
type Stack = List[Int]
import cats._, cats.data._, cats.syntax.all._
def stackyStack: State[Stack, Unit] = for {
stackNow <- State.get[Stack]
r <- if (stackNow === List(1, 2, 3)) State.set[Stack](List(8, 3, 1))
else State.set[Stack](List(9, 2, 1))
} yield r
stackyStack.run(List(1, 2, 3)).value
// res4: (Stack, Unit) = (List(8, 3, 1), ())
pop と push も get と set を使って実装できる:
val pop: State[Stack, Int] = for {
s <- State.get[Stack]
(x :: xs) = s
_ <- State.set[Stack](xs)
} yield x
// pop: State[Stack, Int] = cats.data.IndexedStateT@2e99eeb1
def push(x: Int): State[Stack, Unit] = for {
xs <- State.get[Stack]
r <- State.set(x :: xs)
} yield r
見ての通りモナドそのものはあんまり大したこと無い (タプルを返す関数のカプセル化) けど、連鎖することでボイラープレートを省くことができた。
状態の抽出と変更
State.get と State.set の少しだけ高度なバリエーションとして、
State.extract(f) と State.modify(f) がある。
State.extract(f) は関数 f: S => T を状態 s に適用した結果を戻り値として返すが、状態そのものは変更しない。
逆に、State.modify は関数 f: S => T を状態 s に適用した結果を保存するが、戻り値として () を返す。
Validated データ型
LYAHFGG:
Either e a型も失敗の文脈を与えるモナドです。しかも、失敗に値を付加できるので、何が失敗したかを説明したり、そのほか失敗にまつわる有用な情報を提供できます。
標準ライブラリの Either[A, B] は知ってるし、Cats が Either の右バイアスのファンクターを実装するという話も何回か出てきた。
Validated という、Either の代わりに使えるデータ型がもう1つ Cats に定義されている:
sealed abstract class Validated[+E, +A] extends Product with Serializable {
def fold[B](fe: E => B, fa: A => B): B =
this match {
case Invalid(e) => fe(e)
case Valid(a) => fa(a)
}
def isValid: Boolean = fold(_ => false, _ => true)
def isInvalid: Boolean = fold(_ => true, _ => false)
....
}
object Validated extends ValidatedInstances with ValidatedFunctions{
final case class Valid[+A](a: A) extends Validated[Nothing, A]
final case class Invalid[+E](e: E) extends Validated[E, Nothing]
}
値はこのように作る:
import cats._, cats.data._, cats.syntax.all._
import Validated.{ valid, invalid }
valid[String, String]("event 1 ok")
// res0: Validated[String, String] = Valid(a = "event 1 ok")
invalid[String, String]("event 1 failed!")
// res1: Validated[String, String] = Invalid(e = "event 1 failed!")
Validated の違いはこれはモナドではなく、applicative functor を形成することだ。
最初のイベントの結果を次へと連鎖するのでは無く、Validated は全イベントを検証する:
val result = (valid[String, String]("event 1 ok"),
invalid[String, String]("event 2 failed!"),
invalid[String, String]("event 3 failed!")) mapN {_ + _ + _}
// result: Validated[String, String] = Invalid(
// e = "event 2 failed!event 3 failed!"
// )
最終結果は Invalid(event 2 failed!event 3 failed!) となった。
計算途中でショートさせた Xor のモナドと違って、Validated は計算を続行して全ての失敗を報告する。
これはおそらくオンラインのベーコンショップでユーザのインプットを検証するのに役立つと思う。
だけど、問題はエラーメッセージが 1つの文字列にゴチャっと一塊になってしまっていることだ。リストでも使うべきじゃないか?
NonEmptyList を用いた失敗値の蓄積
ここで使われるのが NonEmptyList データ型だ。
今のところは、必ず 1つ以上の要素が入っていることを保証するリストだと考えておけばいいと思う。
import cats.data.{ NonEmptyList => NEL }
NEL.of(1)
// res2: NonEmptyList[Int] = NonEmptyList(head = 1, tail = List())
NEL[A] を invalid 側に使って失敗値の蓄積を行うことができる:
val result2 =
(valid[NEL[String], String]("event 1 ok"),
invalid[NEL[String], String](NEL.of("event 2 failed!")),
invalid[NEL[String], String](NEL.of("event 3 failed!"))) mapN {_ + _ + _}
// result2: Validated[NonEmptyList[String], String] = Invalid(
// e = NonEmptyList(head = "event 2 failed!", tail = List("event 3 failed!"))
// )
Invalid の中に全ての失敗メッセージが入っている。
fold を使って値を取り出してみる:
val errs: NEL[String] = result2.fold(
{ l => l },
{ r => sys.error("invalid is expected") }
)
// errs: NonEmptyList[String] = NonEmptyList(
// head = "event 2 failed!",
// tail = List("event 3 failed!")
// )
Ior データ型
Cats には A と B のペアを表すデータ型がもう1つあって、
Ior と呼ばれている。
/** Represents a right-biased disjunction that is either an `A`, or a `B`, or both an `A` and a `B`.
*
* An instance of `A [[Ior]] B` is one of:
* - `[[Ior.Left Left]][A]`
* - `[[Ior.Right Right]][B]`
* - `[[Ior.Both Both]][A, B]`
*
* `A [[Ior]] B` is similar to `A [[Xor]] B`, except that it can represent the simultaneous presence of
* an `A` and a `B`. It is right-biased like [[Xor]], so methods such as `map` and `flatMap` operate on the
* `B` value. Some methods, like `flatMap`, handle the presence of two [[Ior.Both Both]] values using a
* `[[Semigroup]][A]`, while other methods, like [[toXor]], ignore the `A` value in a [[Ior.Both Both]].
*
* `A [[Ior]] B` is isomorphic to `(A [[Xor]] B) [[Xor]] (A, B)`, but provides methods biased toward `B`
* values, regardless of whether the `B` values appear in a [[Ior.Right Right]] or a [[Ior.Both Both]].
* The isomorphic [[Xor]] form can be accessed via the [[unwrap]] method.
*/
sealed abstract class Ior[+A, +B] extends Product with Serializable {
final def fold[C](fa: A => C, fb: B => C, fab: (A, B) => C): C = this match {
case Ior.Left(a) => fa(a)
case Ior.Right(b) => fb(b)
case Ior.Both(a, b) => fab(a, b)
}
final def isLeft: Boolean = fold(_ => true, _ => false, (_, _) => false)
final def isRight: Boolean = fold(_ => false, _ => true, (_, _) => false)
final def isBoth: Boolean = fold(_ => false, _ => false, (_, _) => true)
....
}
object Ior extends IorInstances with IorFunctions {
final case class Left[+A](a: A) extends (A Ior Nothing)
final case class Right[+B](b: B) extends (Nothing Ior B)
final case class Both[+A, +B](a: A, b: B) extends (A Ior B)
}
これらの値は Ior の left、right、both メソッドを使って定義する:
import cats._, cats.data._, cats.syntax.all._
import cats.data.{ NonEmptyList => NEL }
Ior.right[NEL[String], Int](1)
// res0: Ior[NonEmptyList[String], Int] = Right(b = 1)
Ior.left[NEL[String], Int](NEL.of("error"))
// res1: Ior[NonEmptyList[String], Int] = Left(
// a = NonEmptyList(head = "error", tail = List())
// )
Ior.both[NEL[String], Int](NEL.of("warning"), 1)
// res2: Ior[NonEmptyList[String], Int] = Both(
// a = NonEmptyList(head = "warning", tail = List()),
// b = 1
// )
scaladoc コメントに書いてある通り、Ior の flatMap は
Ior.both(...) 値をみると Semigroup[A] を用いて失敗値を累積 (accumulate) する。
そのため、これは Xor と Validated のハイブリッドのような感覚で使えるかもしれない。
flatMap の振る舞いを 9つ全ての組み合わせでみてみよう:
Ior.right[NEL[String], Int](1) >>=
{ x => Ior.right[NEL[String], Int](x + 1) }
// res3: Ior[NonEmptyList[String], Int] = Right(b = 2)
Ior.left[NEL[String], Int](NEL.of("error 1")) >>=
{ x => Ior.right[NEL[String], Int](x + 1) }
// res4: Ior[NonEmptyList[String], Int] = Left(
// a = NonEmptyList(head = "error 1", tail = List())
// )
Ior.both[NEL[String], Int](NEL.of("warning 1"), 1) >>=
{ x => Ior.right[NEL[String], Int](x + 1) }
// res5: Ior[NonEmptyList[String], Int] = Both(
// a = NonEmptyList(head = "warning 1", tail = List()),
// b = 2
// )
Ior.right[NEL[String], Int](1) >>=
{ x => Ior.left[NEL[String], Int](NEL.of("error 2")) }
// res6: Ior[NonEmptyList[String], Int] = Left(
// a = NonEmptyList(head = "error 2", tail = List())
// )
Ior.left[NEL[String], Int](NEL.of("error 1")) >>=
{ x => Ior.left[NEL[String], Int](NEL.of("error 2")) }
// res7: Ior[NonEmptyList[String], Int] = Left(
// a = NonEmptyList(head = "error 1", tail = List())
// )
Ior.both[NEL[String], Int](NEL.of("warning 1"), 1) >>=
{ x => Ior.left[NEL[String], Int](NEL.of("error 2")) }
// res8: Ior[NonEmptyList[String], Int] = Left(
// a = NonEmptyList(head = "warning 1", tail = List("error 2"))
// )
Ior.right[NEL[String], Int](1) >>=
{ x => Ior.both[NEL[String], Int](NEL.of("warning 2"), x + 1) }
// res9: Ior[NonEmptyList[String], Int] = Both(
// a = NonEmptyList(head = "warning 2", tail = List()),
// b = 2
// )
Ior.left[NEL[String], Int](NEL.of("error 1")) >>=
{ x => Ior.both[NEL[String], Int](NEL.of("warning 2"), x + 1) }
// res10: Ior[NonEmptyList[String], Int] = Left(
// a = NonEmptyList(head = "error 1", tail = List())
// )
Ior.both[NEL[String], Int](NEL.of("warning 1"), 1) >>=
{ x => Ior.both[NEL[String], Int](NEL.of("warning 2"), x + 1) }
// res11: Ior[NonEmptyList[String], Int] = Both(
// a = NonEmptyList(head = "warning 1", tail = List("warning 2")),
// b = 2
// )
for 内包表記からも使える:
for {
e1 <- Ior.right[NEL[String], Int](1)
e2 <- Ior.both[NEL[String], Int](NEL.of("event 2 warning"), e1 + 1)
e3 <- Ior.both[NEL[String], Int](NEL.of("event 3 warning"), e2 + 1)
} yield (e1 |+| e2 |+| e3)
// res12: Ior[NonEmptyList[String], Int] = Both(
// a = NonEmptyList(head = "event 2 warning", tail = List("event 3 warning")),
// b = 6
// )
Ior.left は Xor[A, B] や Either[A, B] の失敗値のようにショート回路になるが、
Ior.both は Validated[A, B] のように失敗値を累積させる。
今日はここまで! 続きはまた今度。
8日目
7日目には、状態付きの計算をカプセル化する State データ型をみた。
他にも、Either[A, B] の代替となる 3つのデータ型 Xor、Validated、Ior もみた。
自由モノイド
すごいHaskellたのしく学ぼうから少し寄り道して、自由対象 (free object) を探索してみる。
まずは自由モノイドからみていこう。以下のような文字の集合があるとする:
A = { 'a', 'b', 'c', ... }
A に関する自由モノイド (fee monoid)、A* を以下のように形成することができる:
A* = String
ここでの2項演算子は String の連結 (concatenation) だ。
空文字 "" を単位元 (identity) として使うことでモノイド則を満たすことを証明できるはずだ。
さらに、任意の集合 A に対しても以下のようにして自由モノイドを形成できる:
A* = List[A]
ここでの2項演算子は ::: で、単位元は Nil だ。
自由モノイド M(A) の定義は以下のように与えられる:
M(A) の普遍写像性 (universal mapping property, UMP)
i: A => |M(A)| という関数があって、 任意のモノイド N と任意の関数 f: A => |N| があるとき、 |f_hom| ∘ i = f を満たす一意の準同型写像 (homomorphism) f_hom = M(A) => N がある。これを図示すると以下のようになる。
A の代わりに X を使って図を書いてみる。なお、|N| は Set[N] という意味だ:
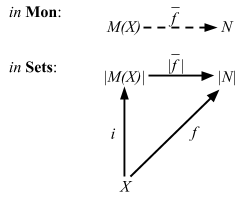
これを Scala を使って考えてみる。
def i(x: X): Set[M[X]] = ???
def f(x: X): Set[N] = ???
// 一意のものが存在する
def f_hom(mx: M[X]): N
// ただし、以下の条件を満たす
def f_hom_set(smx: Set[M[X]]): Set[N] = sma map {f_hom}
f == f_hom_set compose i
ここで A が Char で、N が (Int, +) だとする。
String が自由モノイドを構成するかのプロパティテストを書くことができる。
scala> def i(x: Char): Set[String] = Set(x.toString)
i: (x: Char)Set[String]
scala> def f(x: Char): Set[Int] = Set(x.toInt) // example
f: (x: Char)Set[Int]
scala> val f_hom: PartialFunction[String, Int] =
{ case mx: String if mx.size == 1 => mx.charAt(0).toInt }
f_hom: PartialFunction[String,Int] = <function1>
scala> def f_hom_set(smx: Set[String]): Set[Int] = smx map {f_hom}
f_hom_set: (smx: Set[String])Set[Int]
scala> val g = (f_hom_set _) compose (i _)
g: Char => Set[Int] = <function1>
scala> import org.scalacheck.Prop.forAll
import org.scalacheck.Prop.forAll
scala> val propMAFree = forAll { c: Char => f(c) == g(c) }
propMAFree: org.scalacheck.Prop = Prop
scala> propMAFree.check
+ OK, passed 100 tests.
この実装の f では String は自由みたいだ。
単射
ここから直観として、任意の f を扱うためには Set[M[X]] は X に関してロスレスである必要があることが分かる。
つまり X からの 2値が M[X] 内の同じ値に写像してはいけないということだ。
代数では、これを Char からの射に対して i が単射 (injective) であるという。
定義: もし射 f に関して「任意の射のペア x1: T => A と x2: T => A に対して f ∘ x1 = f ∘ x2 ならば x1 = x2 である」という条件が成り立つ場合、「f は T からの射に関して単射 (injective) である」という。
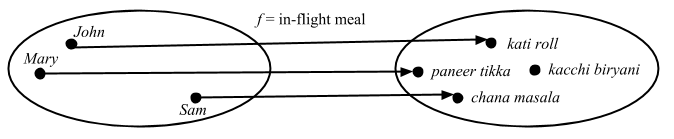
一意性
UMP は f_hom が一意であることを要請するため、Set[M[A]]
が A のゼロ個以上の組み合わせで、それ以外のものは含まないことを要求する。
A に関して M[A] が一意であるため、概念的には集合 A に対して唯一の自由モノイドしか存在しないことになる。
しかし、その自由モノイドは String や List[Char] といったように異なる方法で表現されることもあるため、
実際には自由モノイドの一員といったことになる。
自由対象
実は、自由モノイドは自由対象 (free object) の一例でしかない。
自由対象は函手 (functor) Set[A]: C[A] => Set[A] を使って以下のように定義できる。
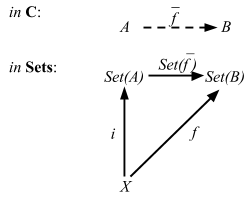
図式を比較すれば、両者ともだいたい似ていることがわかる。
自由モナド (Free)
自由モノイドは自由対象の例だと言った。 同様に、自由モナドも自由対象の例だ。
細かい話は省くが、モナドは自己函手 F: C => C の圏におけるモノイドで、
F × F => F を2項演算子とする。
A から A* を導き出したのと同様に、
任意の自己函手 F から自由モナド F* を導き出すことができる。
Haskell ではこのように行っている:
data Free f a = Pure a | Free (f (Free f a))
instance Functor f => Monad (Free f) where
return = Pure
Pure a >>= f = f a
Free m >>= f = Free ((>>= f) <$> m)
値のリストを保持する
Listと違って、Freeは函手を初期値にラッピングしたもののリストを保持する。 そのため、FreeのFunctorとMonadのインスタンスは、fmapを使って与えられた関数を渡して回る以外のことは何もしない。
また、Free というのはデータ型だけども、Functor ごとに異なる自由モナドが得られることにも注意してほしい。
自由モナドの重要性
実務上では、Free を Functor から Monad を得るための巧妙な手口だと考えることができる。
これは interperter パターンと呼ばれる使い方で特に便利で、
Gabriel Gonzalez (@gabrielg439) さんの
Why free monads matter で解説されている。
構文木の本質を表す抽象体を考えてみよう。[中略]
僕らの toy 言語には 3つのコマンドしかない:
output b -- prints a "b" to the console
bell -- rings the computer's bell
done -- end of execution
次のコマンドが前のコマンドの子ノードであるような構文木としてあらわしてみる:
data Toy b next =
Output b next
| Bell next
| Done
とりあえずこれを素直に Scala に翻訳するとこうなる:
sealed trait Toy[+A, +Next]
object Toy {
case class Output[A, Next](a: A, next: Next) extends Toy[A, Next]
case class Bell[Next](next: Next) extends Toy[Nothing, Next]
case class Done() extends Toy[Nothing, Nothing]
}
Toy.Output('A', Toy.Done())
// res0: Toy.Output[Char, Toy.Done] = Output(a = 'A', next = Done())
Toy.Bell(Toy.Output('A', Toy.Done()))
// res1: Toy.Bell[Toy.Output[Char, Toy.Done]] = Bell(
// next = Output(a = 'A', next = Done())
// )
CharToy
WFMM の DSL はアウトプット用のデータ型を型パラメータとして受け取るので、任意のアウトプット型を扱うことができる。
上に Toy として示したように Scala も同じことができる。だけども、Scala の部分適用型の処理がヘボいため Free の説明としては不必要に複雑となってしまう。そのため、本稿では、以下のようにデータ型を Char に決め打ちしたものを使う:
sealed trait CharToy[+Next]
object CharToy {
case class CharOutput[Next](a: Char, next: Next) extends CharToy[Next]
case class CharBell[Next](next: Next) extends CharToy[Next]
case class CharDone() extends CharToy[Nothing]
def output[Next](a: Char, next: Next): CharToy[Next] = CharOutput(a, next)
def bell[Next](next: Next): CharToy[Next] = CharBell(next)
def done: CharToy[Nothing] = CharDone()
}
{
import CharToy._
output('A', done)
}
// res2: CharToy[CharToy[Nothing]] = CharOutput(a = 'A', next = CharDone())
{
import CharToy._
bell(output('A', done))
}
// res3: CharToy[CharToy[CharToy[Nothing]]] = CharBell(
// next = CharOutput(a = 'A', next = CharDone())
// )
型を CharToy に統一するため、小文字の output、bell、done を加えた。
Fix
WFMM:
しかし残念なことに、コマンドを追加するたびに型が変わってしまうのでこれはうまくいかない。
Fix を定義しよう:
case class Fix[F[_]](f: F[Fix[F]])
object Fix {
def fix(toy: CharToy[Fix[CharToy]]) = Fix[CharToy](toy)
}
{
import Fix._, CharToy._
fix(output('A', fix(done)))
}
// res4: Fix[CharToy] = Fix(
// f = CharOutput(a = 'A', next = Fix(f = CharDone()))
// )
{
import Fix._, CharToy._
fix(bell(fix(output('A', fix(done)))))
}
// res5: Fix[CharToy] = Fix(
// f = CharBell(next = Fix(f = CharOutput(a = 'A', next = Fix(f = CharDone()))))
// )
ここでも fix を提供して型推論が動作するようにした。
FixE
これに例外処理を加えた FixE も実装してみる。throw と catch は予約語なので、throwy、catchy という名前に変える:
import cats._, cats.data._, cats.syntax.all._
sealed trait FixE[F[_], E]
object FixE {
case class Fix[F[_], E](f: F[FixE[F, E]]) extends FixE[F, E]
case class Throwy[F[_], E](e: E) extends FixE[F, E]
def fix[E](toy: CharToy[FixE[CharToy, E]]): FixE[CharToy, E] =
Fix[CharToy, E](toy)
def throwy[F[_], E](e: E): FixE[F, E] = Throwy(e)
def catchy[F[_]: Functor, E1, E2](ex: => FixE[F, E1])
(f: E1 => FixE[F, E2]): FixE[F, E2] = ex match {
case Fix(x) => Fix[F, E2](Functor[F].map(x) {catchy(_)(f)})
case Throwy(e) => f(e)
}
}
これを実際に使うには Toy b が functor である必要があるので、型検査が通るまで色々試してみる (Functor則を満たす必要もある)。
CharToy の Functor はこんな感じになった:
implicit val charToyFunctor: Functor[CharToy] = new Functor[CharToy] {
def map[A, B](fa: CharToy[A])(f: A => B): CharToy[B] = fa match {
case o: CharToy.CharOutput[A] => CharToy.CharOutput(o.a, f(o.next))
case b: CharToy.CharBell[A] => CharToy.CharBell(f(b.next))
case CharToy.CharDone() => CharToy.CharDone()
}
}
// charToyFunctor: Functor[CharToy] = repl.MdocSession1@5f46c659
これがサンプルの使用例だ:
{
import FixE._, CharToy._
case class IncompleteException()
def subroutine = fix[IncompleteException](
output('A',
throwy[CharToy, IncompleteException](IncompleteException())))
def program = catchy[CharToy, IncompleteException, Nothing](subroutine) { _ =>
fix[Nothing](bell(fix[Nothing](done)))
}
}
型パラメータでゴテゴテになってるのはちょっと残念な感じだ。
Free データ型
WFMM:
僕らの
FixEは既に存在していて、それは Free モナドと呼ばれる:
data Free f r = Free (f (Free f r)) | Pure r
名前の通り、これは自動的にモナドだ (ただし、
fが Functor の場合)
instance (Functor f) => Monad (Free f) where
return = Pure
(Free x) >>= f = Free (fmap (>>= f) x)
(Pure r) >>= f = f r
僕達の
Throwはreturnとなって、僕達のcatchは(>>=)に対応する。
Cats でのデータ型は Free と呼ばれる:
/**
* A free operational monad for some functor `S`. Binding is done
* using the heap instead of the stack, allowing tail-call
* elimination.
*/
sealed abstract class Free[S[_], A] extends Product with Serializable {
final def map[B](f: A => B): Free[S, B] =
flatMap(a => Pure(f(a)))
/**
* Bind the given continuation to the result of this computation.
* All left-associated binds are reassociated to the right.
*/
final def flatMap[B](f: A => Free[S, B]): Free[S, B] =
Gosub(this, f)
....
}
object Free {
/**
* Return from the computation with the given value.
*/
private final case class Pure[S[_], A](a: A) extends Free[S, A]
/** Suspend the computation with the given suspension. */
private final case class Suspend[S[_], A](a: S[A]) extends Free[S, A]
/** Call a subroutine and continue with the given function. */
private final case class Gosub[S[_], B, C](c: Free[S, C], f: C => Free[S, B]) extends Free[S, B]
/**
* Suspend a value within a functor lifting it to a Free.
*/
def liftF[F[_], A](value: F[A]): Free[F, A] = Suspend(value)
/** Suspend the Free with the Applicative */
def suspend[F[_], A](value: => Free[F, A])(implicit F: Applicative[F]): Free[F, A] =
liftF(F.pure(())).flatMap(_ => value)
/** Lift a pure value into Free */
def pure[S[_], A](a: A): Free[S, A] = Pure(a)
final class FreeInjectPartiallyApplied[F[_], G[_]] private[free] {
def apply[A](fa: F[A])(implicit I : Inject[F, G]): Free[G, A] =
Free.liftF(I.inj(fa))
}
def inject[F[_], G[_]]: FreeInjectPartiallyApplied[F, G] = new FreeInjectPartiallyApplied
....
}
これらのデータ型を使うには Free.liftF を使う:
import cats.free.Free
sealed trait CharToy[+Next]
object CharToy {
case class CharOutput[Next](a: Char, next: Next) extends CharToy[Next]
case class CharBell[Next](next: Next) extends CharToy[Next]
case class CharDone() extends CharToy[Nothing]
implicit val charToyFunctor: Functor[CharToy] = new Functor[CharToy] {
def map[A, B](fa: CharToy[A])(f: A => B): CharToy[B] = fa match {
case o: CharOutput[A] => CharOutput(o.a, f(o.next))
case b: CharBell[A] => CharBell(f(b.next))
case CharDone() => CharDone()
}
}
def output(a: Char): Free[CharToy, Unit] =
Free.liftF[CharToy, Unit](CharOutput(a, ()))
def bell: Free[CharToy, Unit] = Free.liftF[CharToy, Unit](CharBell(()))
def done: Free[CharToy, Unit] = Free.liftF[CharToy, Unit](CharDone())
def pure[A](a: A): Free[CharToy, A] = Free.pure[CharToy, A](a)
}
コマンドのシーケンスはこんな感じになる:
import CharToy._
val subroutine = output('A')
// subroutine: Free[CharToy, Unit] = Suspend(
// a = CharOutput(a = 'A', next = ())
// )
val program = for {
_ <- subroutine
_ <- bell
_ <- done
} yield ()
// program: Free[CharToy, Unit] = FlatMapped(
// c = Suspend(a = CharOutput(a = 'A', next = ())),
// f = <function1>
// )
面白くなってきた。「まだ評価されていないもの」に対する
do記法を得られることができた。これは純粋なデータだ。
次に、これが本当に純粋なデータであることを証明するために showProgram を定義する:
def showProgram[R: Show](p: Free[CharToy, R]): String =
p.fold({ r: R => "return " + Show[R].show(r) + "\n" },
{
case CharOutput(a, next) =>
"output " + Show[Char].show(a) + "\n" + showProgram(next)
case CharBell(next) =>
"bell " + "\n" + showProgram(next)
case CharDone() =>
"done\n"
})
showProgram(program)
// res8: String = """output A
// bell
// done
// """
Free を使って生成したモナドがモナド則を満たしているか手で確かめてみる:
showProgram(output('A'))
// res9: String = """output A
// return ()
// """
showProgram(pure('A') flatMap output)
// res10: String = """output A
// return ()
// """
showProgram(output('A') flatMap pure)
// res11: String = """output A
// return ()
// """
showProgram((output('A') flatMap { _ => done }) flatMap { _ => output('C') })
// res12: String = """output A
// done
// """
showProgram(output('A') flatMap { _ => (done flatMap { _ => output('C') }) })
// res13: String = """output A
// done
// """
うまくいった。done が abort的な意味論になっていることにも注目してほしい。
型推論の制約上、>>= と >> をここでは使うことができなかった。
WFMM:
Free モナドはインタプリタの良き友だ。Free モナドはインタプリタを限りなく「解放 (free) 」しつつも必要最低限のモナドの条件を満たしている。
もう一つの見方としては、Free は与えられたコンテナを使って構文木を作る方法を提供する。
Free データ型が人気を得ているのは、異なるモナドの合成した場合の制約に色んな人がハマってるからではないかと思う。
モナド変換子を使えば不可能ではないけども、型シグネチャはすぐにゴチャゴチャになるし、積み上げた型がコードの色んな所に漏れ出す。
その反面、Free はモナドに意味を持たせることを諦める代わりに、インタープリター関数で好き勝手できる柔軟性を得る。
例えば、テストでは逐次実行して、本番では並列で走らせるということもできるはずだ。
Stackless Scala with Free Monads
自由モナドの概念は interpreter パターンを超えたものだ。 恐らくこれからも新しい自由モナドの応用範囲が見つかっていくと思う。
Rúnar (@runarorama) さんは Scala で Free を使うことを広めた第一人者だ。
6日目に扱った Dead-Simple Dependency Injection というトークでは
key-value ストアを実装するためのミニ言語を Free を用いて実装していた。
同年の Scala Days 2012 では Rúnar さんは
Stackless Scala With Free Monads というトークをやっている。
ペーパーを読む前にトークを観ておくことをお勧めするけど、ペーパーの方が引用しやすいので
Stackless Scala With Free Monads もリンクしておく。
Rúnar さんはまず State モナドの実装を使ってリストに添字を zip するコードから始める。 これはリストがスタックの限界よりも大きいと、スタックを吹っ飛ばす。 続いてプログラム全体を一つのループで回すトランポリンというものを紹介している。
sealed trait Trampoline [+ A] {
final def runT : A =
this match {
case More (k) => k().runT
case Done (v) => v
}
}
case class More[+A](k: () => Trampoline[A])
extends Trampoline[A]
case class Done [+A](result: A)
extends Trampoline [A]
上記のコードでは Function0 の k は次のステップのための thunk となっている。
これを State モナドを使った使用例に拡張するため、flatMap を FlatMap というデータ構造に具現化している:
case class FlatMap [A,+B](
sub: Trampoline [A],
k: A => Trampoline[B]) extends Trampoline[B]
続いて、Trampoline は実は Function0 の Free モナドであることが明かされる。
Cats では以下のように定義されている:
type Trampoline[A] = Free[Function0, A]
トランポリン
トランポリンを使えば、どんなプログラムでもスタックを使わないものに変換することができる。
Trampoine object はトランポリン化するのに役立つ関数を定義する:
object Trampoline {
def done[A](a: A): Trampoline[A] =
Free.Pure[Function0,A](a)
def suspend[A](a: => Trampoline[A]): Trampoline[A] =
Free.Suspend[Function0, A](() => a)
def delay[A](a: => A): Trampoline[A] =
suspend(done(a))
}
トークに出てきた even と odd を実装してみよう:
import cats._, cats.syntax.all._, cats.free.{ Free, Trampoline }
import Trampoline._
def even[A](ns: List[A]): Trampoline[Boolean] =
ns match {
case Nil => done(true)
case x :: xs => defer(odd(xs))
}
def odd[A](ns: List[A]): Trampoline[Boolean] =
ns match {
case Nil => done(false)
case x :: xs => defer(even(xs))
}
even(List(1, 2, 3)).run
// res0: Boolean = false
even((0 to 3000).toList).run
// res1: Boolean = false
上を実装してるうちにまた SI-7139 に引っかかったので、Cats を少し改良する必要があった。 #322
自由モナド
さらに Rúnar さんは便利な Free モナドを作れるいくつかのデータ型を紹介する:
type Pair[+A] = (A, A)
type BinTree[+A] = Free[Pair, A]
type Tree[+A] = Free[List, A]
type FreeMonoid[+A] = Free[({type λ[+α] = (A,α)})#λ, Unit]
type Trivial[+A] = Unit
type Option[+A] = Free[Trivial, A]
モナドを使った Iteratee まであるみたいだ。最後に自由モナドを以下のようにまとめている:
- データが末端に来る全ての再帰データ型に使えるモデル
- 自由モナドは変数が末端にある式木で、flatMap は変数の置換にあたる。
Free を用いた自由モノイド
Free を使って「リスト」を定義してみよう。
type FreeMonoid[A] = Free[(A, +*), Unit]
def cons[A](a: A): FreeMonoid[A] =
Free.liftF[(A, +*), Unit]((a, ()))
val x = cons(1)
// x: FreeMonoid[Int] = Suspend(a = (1, ()))
val xs = cons(1) flatMap { _ => cons(2) }
// xs: Free[(Int, β0), Unit] = FlatMapped(
// c = Suspend(a = (1, ())),
// f = <function1>
// )
この結果を処理する一例として標準の List に変換してみる:
implicit def tuple2Functor[A]: Functor[(A, *)] =
new Functor[(A, *)] {
def map[B, C](fa: (A, B))(f: B => C) =
(fa._1, f(fa._2))
}
def toList[A](list: FreeMonoid[A]): List[A] =
list.fold(
{ _ => Nil },
{ case (x: A @unchecked, xs: FreeMonoid[A]) => x :: toList(xs) })
toList(xs)
// res2: List[Int] = List(1, 2)
末尾再帰モナド (FlatMap)
2015年に PureScript でのスタック安全性の取り扱いに関して Phil Freeman (@paf31) さんは Stack Safety for Free を書いた。 PureScript は Scala 同様に正格 (strict) な JavaScript にホストされている言語だ:
I've written up some work on stack safe free monad transformers. Feedback would be very much appreciated http://t.co/1rH7OwaWpy
— Phil Freeman (@paf31) August 8, 2015
この論文は Rúnar (@runarorama) さんの Stackless Scala With Free Monads にも言及するが、スタック安全性に関してより抜本的な解法を提示している。
スタック問題とは
問題の背景として、Scala ではコンパイラが自己再帰の末尾再帰呼び出しは最適化することが可能だ。
例えば、これは自己再帰の末尾再帰呼び出しの例だ。
import scala.annotation.tailrec
def pow(n: Long, exp: Long): Long =
{
@tailrec def go(acc: Long, p: Long): Long =
(acc, p) match {
case (acc, 0) => acc
case (acc, p) => go(acc * n, p - 1)
}
go(1, exp)
}
pow(2, 3)
// res0: Long = 8L
自己再帰じゃない例。スタックオーバーフローを起こしている。
scala> :paste
object OddEven0 {
def odd(n: Int): String = even(n - 1)
def even(n: Int): String = if (n <= 0) "done" else odd(n - 1)
}
// Exiting paste mode, now interpreting.
defined object OddEven0
scala> OddEven0.even(200000)
java.lang.StackOverflowError
at OddEven0$.even(<console>:15)
at OddEven0$.odd(<console>:14)
at OddEven0$.even(<console>:15)
at OddEven0$.odd(<console>:14)
at OddEven0$.even(<console>:15)
....
次に、pow に Writer データ型を追加して、LongProduct モノイドを使って計算をさせてみたい。
import cats._, cats.data._, cats.syntax.all._
case class LongProduct(value: Long)
implicit val longProdMonoid: Monoid[LongProduct] = new Monoid[LongProduct] {
def empty: LongProduct = LongProduct(1)
def combine(x: LongProduct, y: LongProduct): LongProduct = LongProduct(x.value * y.value)
}
// longProdMonoid: Monoid[LongProduct] = repl.MdocSession1@63b4190b
def powWriter(x: Long, exp: Long): Writer[LongProduct, Unit] =
exp match {
case 0 => Writer(LongProduct(1L), ())
case m =>
Writer(LongProduct(x), ()) >>= { _ => powWriter(x, exp - 1) }
}
powWriter(2, 3).run
// res1: (LongProduct, Unit) = (LongProduct(value = 8L), ())
自己再帰じゃなくなったので、exp の値が大きいとスタックオーバーフローするようになってしまった。
scala> powWriter(1, 10000).run
java.lang.StackOverflowError
at $anonfun$powWriter$1.apply(<console>:35)
at $anonfun$powWriter$1.apply(<console>:35)
at cats.data.WriterT$$anonfun$flatMap$1.apply(WriterT.scala:37)
at cats.data.WriterT$$anonfun$flatMap$1.apply(WriterT.scala:36)
at cats.package$$anon$1.flatMap(package.scala:34)
at cats.data.WriterT.flatMap(WriterT.scala:36)
at cats.data.WriterTFlatMap1$class.flatMap(WriterT.scala:249)
at cats.data.WriterTInstances2$$anon$4.flatMap(WriterT.scala:130)
at cats.data.WriterTInstances2$$anon$4.flatMap(WriterT.scala:130)
at cats.FlatMap$class.$greater$greater$eq(FlatMap.scala:26)
at cats.data.WriterTInstances2$$anon$4.$greater$greater$eq(WriterT.scala:130)
at cats.FlatMap$Ops$class.$greater$greater$eq(FlatMap.scala:20)
at cats.syntax.FlatMapSyntax1$$anon$1.$greater$greater$eq(flatMap.scala:6)
at .powWriter1(<console>:35)
at $anonfun$powWriter$1.apply(<console>:35)
この Scala の特性は flatMap がモナディック関数を呼び出して、さらにそれが flatMap
を呼び出すといった形のモナディック合成の便利さを制限するものだ。
FlatMap (MonadRec)
我々がとった対策方法はモナド
mの対象を任意のモナドから、いわゆる末尾再帰モナドとよばれる型クラスに候補を狭めたことだ。
class (Monad m) <= MonadRec m where
tailRecM :: forall a b. (a -> m (Either a b)) -> a -> m b
Scala で同じ関数を書くとこうなる:
/**
* Keeps calling `f` until a `scala.util.Right[B]` is returned.
*/
def tailRecM[A, B](a: A)(f: A => F[Either[A, B]]): F[B]
実は Oscar Boykin (@posco) さんが #1280 (Remove FlatMapRec make all FlatMap implement tailRecM)
において、この tailRecM を FlatMap に持ち込んでいて、Cats 0.7.0 の一部となっている。
つまり、Cats 0.7.0 以降の FlatMap/Monad は末尾再帰であると言うことができる。
例えば、Writer の tailRecM を以下のようにして取得できる:
def tailRecM[A, B] = FlatMap[Writer[Vector[String], *]].tailRecM[A, B] _
スタックセーフな powWriter はこう書くことができる:
def powWriter2(x: Long, exp: Long): Writer[LongProduct, Unit] =
FlatMap[Writer[LongProduct, *]].tailRecM(exp) {
case 0L => Writer.value[LongProduct, Either[Long, Unit]](Right(()))
case m: Long => Writer.tell(LongProduct(x)) >>= { _ => Writer.value(Left(m - 1)) }
}
powWriter2(2, 3).run
// res2: (LongProduct, Unit) = (LongProduct(value = 8L), ())
powWriter2(1, 10000).run
// res3: (LongProduct, Unit) = (LongProduct(value = 1L), ())
これは FlatMap 型クラスのユーザにとってはより大きな安全性を保証するものだが、
インスタンスの実装する者は安全な tailRecM を提供しなければいけないことも意味している。
例えば Option の実装はこんな感じだ:
@tailrec
def tailRecM[A, B](a: A)(f: A => Option[Either[A, B]]): Option[B] =
f(a) match {
case None => None
case Some(Left(a1)) => tailRecM(a1)(f)
case Some(Right(b)) => Some(b)
}
今日はここまで。
9日目
8日目は、Ior データ型、自由モノイド、自由モナド、そして
Trampoline データ型をみた。
便利なモナディック関数特集
この節では、モナド値を操作したり、モナド値を返したりする関数(両方でも可!)をいくつか紹介します。そんな関数はモナディック関数と呼ばれます。
Haskell 標準の Monad と違って Cats の Monad は後知恵である
より弱い型クラスを用いた粒度の高い設計となっている。
Monad- extends
FlatMapandApplicative - extends
Apply - extends
Functor
そのため、全てのモナドがアプリカティブ・ファンクターとファンクターであることは自明となっていて、
モナドを形成する全てのデータ型に対して ap や map 演算子を使うことができる。
flatten メソッド
LYAHFGG:
実は、任意の入れ子になったモナドは平らにできるんです。そして実は、これはモナド特有の性質なのです。このために、
joinという関数が用意されています。
Cats でこれに当たる関数は flatten と呼ばれており、FlatMap にて定義されている。
simulacrum のお陰で flatten はメソッドとしても導入されている。
@typeclass trait FlatMap[F[_]] extends Apply[F] {
def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B]
/**
* also commonly called join
*/
def flatten[A](ffa: F[F[A]]): F[A] =
flatMap(ffa)(fa => fa)
....
}
Option[A] は既に flatten を実装するので、
これを抽象型にするために抽象関数を書く必要がある。
import cats._, cats.syntax.all._
def join[F[_]: FlatMap, A](fa: F[F[A]]): F[A] =
fa.flatten
join(1.some.some)
// res0: Option[Int] = Some(value = 1)
どうせ関数にしてしまうのなら、関数構文をそのまま使えばいい。
FlatMap[Option].flatten(1.some.some)
// res1: Option[Int] = Some(value = 1)
filterM メソッド
LYAHFGG:
Control.MonadモジュールのfilterMこそ、まさにそのための関数です! … 述語はBoolを結果とするモナド値を返しています。
Cats では filterM を提供しないが、TraverseFilter に filterA がある。
foldM 関数
LYAHFGG:
foldlのモナド版がfoldMです。
Cats には foldM が無いみたいだったので、自分で定義してみたけどもスタック・セーフじゃなかった。Tomas Mikula がそれを修正した実装を追加してくれて、それが #925 でマージされた。
/**
* Left associative monadic folding on `F`.
*/
def foldM[G[_], A, B](fa: F[A], z: B)(f: (B, A) => G[B])(implicit G: Monad[G]): G[B] =
foldLeft(fa, G.pure(z))((gb, a) => G.flatMap(gb)(f(_, a)))
使ってみる。
def binSmalls(acc: Int, x: Int): Option[Int] =
if (x > 9) none[Int] else (acc + x).some
(Foldable[List].foldM(List(2, 8, 3, 1), 0) {binSmalls})
// res2: Option[Int] = Some(value = 14)
(Foldable[List].foldM(List(2, 11, 3, 1), 0) {binSmalls})
// res3: Option[Int] = None
上の例では binSmals が 9 より多きい数を見つけると None を返す。
安全な RPN 電卓を作ろう
LYAHFGG:
第10章で逆ポーランド記法 (RPN) の電卓を実装せよという問題を解いたときには、この電卓は文法的に正しい入力が与えられる限り正しく動くよ、という注意書きがありました。
最初に RPN 電卓を作った章は飛ばしたけど、コードはここにあるから Scala に訳してみる:
def foldingFunction(list: List[Double], next: String): List[Double] =
(list, next) match {
case (x :: y :: ys, "*") => (y * x) :: ys
case (x :: y :: ys, "+") => (y + x) :: ys
case (x :: y :: ys, "-") => (y - x) :: ys
case (xs, numString) => numString.toInt :: xs
}
def solveRPN(s: String): Double =
(s.split(' ').toList
.foldLeft(Nil: List[Double]) {foldingFunction}).head
solveRPN("10 4 3 + 2 * -")
// res0: Double = -4.0
動作しているみたいだ。
次に畳み込み関数がエラーを処理できるようにする。parseInt は以下のように実装できる:
import scala.util.Try
def parseInt(x: String): Option[Int] =
(scala.util.Try(x.toInt) map { Some(_) }
recover { case _: NumberFormatException => None }).get
parseInt("1")
// res2: Option[Int] = Some(value = 1)
parseInt("foo")
// res3: Option[Int] = None
以下が更新された畳込み関数:
import cats._, cats.syntax.all._
def foldingFunction(list: List[Double], next: String): Option[List[Double]] =
(list, next) match {
case (x :: y :: ys, "*") => ((y * x) :: ys).some
case (x :: y :: ys, "+") => ((y + x) :: ys).some
case (x :: y :: ys, "-") => ((y - x) :: ys).some
case (xs, numString) => parseInt(numString) map {_ :: xs}
}
foldingFunction(List(3, 2), "*")
// res4: Option[List[Double]] = Some(value = List(6.0))
foldingFunction(Nil, "*")
// res5: Option[List[Double]] = None
foldingFunction(Nil, "wawa")
// res6: Option[List[Double]] = None
以下が foldM を用いて書いた solveRPN だ:
def solveRPN(s: String): Option[Double] =
for {
List(x) <- (Foldable[List].foldM(s.split(' ').toList,
Nil: List[Double]) {foldingFunction})
} yield x
solveRPN("1 2 * 4 +")
// res7: Option[Double] = Some(value = 6.0)
solveRPN("1 2 * 4")
// res8: Option[Double] = None
solveRPN("1 8 garbage")
// res9: Option[Double] = None
モナディック関数の合成
LYAHFGG:
第13章でモナド則を紹介したとき、
<=<関数は関数合成によく似ているど、普通の関数a -> bではなくて、a -> m bみたいなモナディック関数に作用するのだよと言いました。
Cats には Kleisli と呼ばれる A => M[B] という型の関数に対する特殊なラッパーがある:
/**
* Represents a function `A => F[B]`.
*/
final case class Kleisli[F[_], A, B](run: A => F[B]) { self =>
....
}
object Kleisli extends KleisliInstances with KleisliFunctions
private[data] sealed trait KleisliFunctions {
def pure[F[_], A, B](x: B)(implicit F: Applicative[F]): Kleisli[F, A, B] =
Kleisli(_ => F.pure(x))
def ask[F[_], A](implicit F: Applicative[F]): Kleisli[F, A, A] =
Kleisli(F.pure)
def local[M[_], A, R](f: R => R)(fa: Kleisli[M, R, A]): Kleisli[M, R, A] =
Kleisli(f andThen fa.run)
}
Kleisli() コンストラクタを使って Kliesli 値を構築する:
import cats._, cats.data._, cats.syntax.all._
val f = Kleisli { (x: Int) => (x + 1).some }
// f: Kleisli[Option, Int, Int] = Kleisli(run = <function1>)
val g = Kleisli { (x: Int) => (x * 100).some }
// g: Kleisli[Option, Int, Int] = Kleisli(run = <function1>)
compose を使って関数を合成すると、右辺項が先に適用される。
4.some >>= (f compose g).run
// res0: Option[Int] = Some(value = 401)
andThen を使うと、左辺項が先に適用される:
4.some >>= (f andThen g).run
// res1: Option[Int] = Some(value = 500)
compose と andThen は関数の合成同様に動作するが、モナディックなコンテキストを保持するのが違いだ。
lift メソッド
Kleisli には、モナディック関数を別のアプリカティブ・ファンクターに持ち上げる lift のような面白いメソッドがいくつかある。
と思って使ってみたけども、壊れている事に気付いたので、これが修正版だ #354:
def lift[G[_]](implicit G: Applicative[G]): Kleisli[λ[α => G[F[α]]], A, B] =
Kleisli[λ[α => G[F[α]]], A, B](a => Applicative[G].pure(run(a)))
使ってみる:
{
val l = f.lift[List]
List(1, 2, 3) >>= l.run
}
// res2: List[Option[Int]] = List(
// Some(value = 2),
// Some(value = 3),
// Some(value = 4)
// )
モナドを作る
LYAHFGG:
この節では、型が生まれてモナドであると確認され、適切な
Monadインスタンスが与えられるまでの過程を、例題を通して学ぼうと思います。 …[3,5,9]のような非決定的値を表現したいのだけど、さらに3である確率は 50パーセント、5と9である確率はそれぞれ 25パーセントである、ということを表したくなったらどうしましょう?
Scala に有理数が標準で入っていないので、Double を使う。以下が case class:
import cats._, cats.syntax.all._
case class Prob[A](list: List[(A, Double)])
trait ProbInstances {
implicit def probShow[A]: Show[Prob[A]] = Show.fromToString
}
case object Prob extends ProbInstances
これってファンクターでしょうか?ええ、リストはファンクターですから、リストに何かを足したものである
Probもたぶんファンクターでしょう。
case class Prob[A](list: List[(A, Double)])
trait ProbInstances {
implicit val probInstance: Functor[Prob] = new Functor[Prob] {
def map[A, B](fa: Prob[A])(f: A => B): Prob[B] =
Prob(fa.list map { case (x, p) => (f(x), p) })
}
implicit def probShow[A]: Show[Prob[A]] = Show.fromToString
}
case object Prob extends ProbInstances
Prob((3, 0.5) :: (5, 0.25) :: (9, 0.25) :: Nil) map { -_ }
// res1: Prob[Int] = Prob(list = List((-3, 0.5), (-5, 0.25), (-9, 0.25)))
本と同様に flatten をまず実装する。
case class Prob[A](list: List[(A, Double)])
trait ProbInstances {
def flatten[B](xs: Prob[Prob[B]]): Prob[B] = {
def multall(innerxs: Prob[B], p: Double) =
innerxs.list map { case (x, r) => (x, p * r) }
Prob((xs.list map { case (innerxs, p) => multall(innerxs, p) }).flatten)
}
implicit val probInstance: Functor[Prob] = new Functor[Prob] {
def map[A, B](fa: Prob[A])(f: A => B): Prob[B] =
Prob(fa.list map { case (x, p) => (f(x), p) })
}
implicit def probShow[A]: Show[Prob[A]] = Show.fromToString
}
case object Prob extends ProbInstances
これでモナドのための準備は整ったはずだ:
import scala.annotation.tailrec
case class Prob[A](list: List[(A, Double)])
trait ProbInstances { self =>
def flatten[B](xs: Prob[Prob[B]]): Prob[B] = {
def multall(innerxs: Prob[B], p: Double) =
innerxs.list map { case (x, r) => (x, p * r) }
Prob((xs.list map { case (innerxs, p) => multall(innerxs, p) }).flatten)
}
implicit val probInstance: Monad[Prob] = new Monad[Prob] {
def pure[A](a: A): Prob[A] = Prob((a, 1.0) :: Nil)
def flatMap[A, B](fa: Prob[A])(f: A => Prob[B]): Prob[B] = self.flatten(map(fa)(f))
override def map[A, B](fa: Prob[A])(f: A => B): Prob[B] =
Prob(fa.list map { case (x, p) => (f(x), p) })
def tailRecM[A, B](a: A)(f: A => Prob[Either[A, B]]): Prob[B] = {
val buf = List.newBuilder[(B, Double)]
@tailrec def go(lists: List[List[(Either[A, B], Double)]]): Unit =
lists match {
case (ab :: abs) :: tail => ab match {
case (Right(b), p) =>
buf += ((b, p))
go(abs :: tail)
case (Left(a), p) =>
go(f(a).list :: abs :: tail)
}
case Nil :: tail => go(tail)
case Nil => ()
}
go(f(a).list :: Nil)
Prob(buf.result)
}
}
implicit def probShow[A]: Show[Prob[A]] = Show.fromToString
}
case object Prob extends ProbInstances
本によるとモナド則は満たしているらしい。Coin の例題も実装してみよう:
sealed trait Coin
object Coin {
case object Heads extends Coin
case object Tails extends Coin
implicit val coinEq: Eq[Coin] = new Eq[Coin] {
def eqv(a1: Coin, a2: Coin): Boolean = a1 == a2
}
def heads: Coin = Heads
def tails: Coin = Tails
}
import Coin.{heads, tails}
def coin: Prob[Coin] = Prob(heads -> 0.5 :: tails -> 0.5 :: Nil)
def loadedCoin: Prob[Coin] = Prob(heads -> 0.1 :: tails -> 0.9 :: Nil)
flipThree の実装はこうなる:
def flipThree: Prob[Boolean] = for {
a <- coin
b <- coin
c <- loadedCoin
} yield { List(a, b, c) forall {_ === tails} }
flipThree
// res4: Prob[Boolean] = Prob(
// list = List(
// (false, 0.025),
// (false, 0.225),
// (false, 0.025),
// (false, 0.225),
// (false, 0.025),
// (false, 0.225),
// (false, 0.025),
// (true, 0.225)
// )
// )
イカサマのコインを 1つ使っても 3回とも裏が出る確率はかなり低いことが分かった。
モナドはフラクタルだ
5日目に綱渡りの例を使って得られた直観は、
>>= を使ったモナディックなチェインはある演算から次の演算へとコンテキストを引き渡すということだった。
中間値に 1つでも None があっただけで、チェイン全体が島流しとなる。
引き渡されるコンテキストはモナドのインスタンスによって異なる。
例えば、7日目にみた State データ型は、>>=
によって状態オブジェクトの明示的な引き渡しを自動化する。
これはモナドを Functor、Apply や Applicative
と比較したときに有用な直観だけどもストーリーとしては全体像を語らない。

モナド (正確には FlatMap) に関するもう1つの直観は、
これらがシェルピンスキーの三角形のようなフラクタルであることだ。
フラクタルの個々の部分が全体の形の自己相似となっている。
例えば、List を例にとる。複数の List の List は、単一のフラットな List として取り扱うことができる。
val xss = List(List(1), List(2, 3), List(4))
// xss: List[List[Int]] = List(List(1), List(2, 3), List(4))
xss.flatten
// res0: List[Int] = List(1, 2, 3, 4)
この flatten 関数は List データ構造の押し潰しを体現する。
型シグネチャで考えると、これは F[F[A]] => F[A] だと言える。
List は ++ に関してモナドを形成する
平坦化を foldLeft を使って再実装することで、より良い理解を得ることができる:
xss.foldLeft(List(): List[Int]) { _ ++ _ }
// res1: List[Int] = List(1, 2, 3, 4)
これによって List は ++ に関してモナドを形成すると言うことができる。
じゃあ、Option は何に関するモナド?
次に、どの演算に関して Option はモナドを形成しているのが考えてみる:
val o1 = Some(None: Option[Int]): Option[Option[Int]]
// o1: Option[Option[Int]] = Some(value = None)
val o2 = Some(Some(1): Option[Int]): Option[Option[Int]]
// o2: Option[Option[Int]] = Some(value = Some(value = 1))
val o3 = None: Option[Option[Int]]
// o3: Option[Option[Int]] = None
foldLeft で書いてみる:
o1.foldLeft(None: Option[Int]) { (_, _)._2 }
// res2: Option[Int] = None
o2.foldLeft(None: Option[Int]) { (_, _)._2 }
// res3: Option[Int] = Some(value = 1)
o3.foldLeft(None: Option[Int]) { (_, _)._2 }
// res4: Option[Int] = None
Option は (_, _)._2 に関してモナドを形成しているみたいだ。
フラクタルとしての State
フラクタルという視点から State データ型に関してもう一度考えてみると、
State の State がやはり State であることは明らかだ。
この特性を利用することで、pop や push といったミニ・プログラムを書いて、
それらを for 内包表記を用いてより大きな State に合成するといったことが可能となる:
def stackManip: State[Stack, Int] = for {
_ <- push(3)
a <- pop
b <- pop
} yield(b)
このような合成は自由モナドでもみた。
つまり、同じモナド・インスタンスの中ではモナディック値は合成することができる。
フラクタルを探しだす
独自のモナドを発見したいと思ったら、フラクタル構造に気をつけるべきだ。
見つけたら flatten 関数 F[F[A]] => F[A] を実装できるか確かめてみよう。
10日目
9日目は、モナディック関数である flatten、 filterM、そして foldM の実装をみた。
次に foldM を使って安全な RPN 計算機を作り、Kleisli 合成をみて、独自のモナドである Prob を作って、フラクタルとの関係についても考えた。
Cats は Zippper に相当するものを提供しないので、昨日の段階で「すごいHaskellたのしく学ぼう」からのネタは終わりで、
今日からは自分でトピックを考えなければいけない。
これまでも出かかってきてたけど、未だ取り扱っていなかった話題としてモナド変換子という概念がある。 幸いなことに、Haskell の良書でオンライン版も公開されている本がもう 1冊あるので、これを参考にしてみる。
モナド変換子
もし標準の
Stateモナドに何らかの方法でエラー処理を追加することができれば理想的だ。 一から手書きで独自のモナドを作るのは当然避けたい。mtlライブラリに入っている標準のモナド同士を組み合わせることはできない。 だけども、このライブラリはモナド変換子というものを提供して、同じことを実現できる。モナド変換子は通常のモナドに似ているが、孤立して使える実体ではなく、 基盤となる別のモナドの振る舞いを変更するものだ。
Dependency injection 再び
6日目 にみた Reader データ型 (Function1) を DI に使うという考えをもう一度見てみよう。
case class User(id: Long, parentId: Long, name: String, email: String)
trait UserRepo {
def get(id: Long): User
def find(name: String): User
}
Jason Arhart さんの
Scrap Your Cake Pattern Boilerplate: Dependency Injection Using the Reader Monad
は Config オブジェクトを作ることで Reader データ型を複数のサービスのサポートに一般化している:
import java.net.URI
trait HttpService {
def get(uri: URI): String
}
trait Config {
def userRepo: UserRepo
def httpService: HttpService
}
これを使うには Config => A 型のミニ・プログラムを作って、それらを合成する。
ここで、Option を使って失敗という概念もエンコードしたいとする。
ReaderT としての Kleisli
昨日見た Kleisli データ型を ReaderT、つまり Reader データ型のモナド変換子版として使って、それを Option
の上に積み上げることができる:
import cats._, cats.data._, cats.syntax.all._
type ReaderTOption[A, B] = Kleisli[Option, A, B]
object ReaderTOption {
def ro[A, B](f: A => Option[B]): ReaderTOption[A, B] = Kleisli(f)
}
Config を変更して httpService をオプショナルにする:
import java.net.URI
case class User(id: Long, parentId: Long, name: String, email: String)
trait UserRepo {
def get(id: Long): Option[User]
def find(name: String): Option[User]
}
trait HttpService {
def get(uri: URI): String
}
trait Config {
def userRepo: UserRepo
def httpService: Option[HttpService]
}
次に、「プリミティブ」なリーダーが ReaderTOption[Config, A] を返すように書き換える:
trait Users {
def getUser(id: Long): ReaderTOption[Config, User] =
ReaderTOption.ro {
case config => config.userRepo.get(id)
}
def findUser(name: String): ReaderTOption[Config, User] =
ReaderTOption.ro {
case config => config.userRepo.find(name)
}
}
trait Https {
def getHttp(uri: URI): ReaderTOption[Config, String] =
ReaderTOption.ro {
case config => config.httpService map {_.get(uri)}
}
}
これらのミニ・プログラムを合成して複合プログラムを書くことができる:
trait Program extends Users with Https {
def userSearch(id: Long): ReaderTOption[Config, String] =
for {
u <- getUser(id)
r <- getHttp(new URI("http://www.google.com/?q=" + u.name))
} yield r
}
object Main extends Program {
def run(config: Config): Option[String] =
userSearch(2).run(config)
}
val dummyConfig: Config = new Config {
val testUsers = List(User(0, 0, "Vito", "vito@example.com"),
User(1, 0, "Michael", "michael@example.com"),
User(2, 0, "Fredo", "fredo@example.com"))
def userRepo: UserRepo = new UserRepo {
def get(id: Long): Option[User] =
testUsers find { _.id === id }
def find(name: String): Option[User] =
testUsers find { _.name === name }
}
def httpService: Option[HttpService] = None
}
// dummyConfig: Config = repl.MdocSession1@3001e384
上の ReaderTOption データ型は、Reader の設定の読み込む能力と、
Option の失敗を表現できる能力を組み合わせたものとなっている。
複数のモナド変換子を積み上げる
RWH:
普通のモナドにモナド変換子を積み上げると、別のモナドになる。 これは組み合わされたモナドの上にさらにモナド変換子を積み上げて、新しいモナドを作ることができる可能性を示唆する。 実際に、これはよく行われていることだ。
状態遷移を表す StateT を ReaderTOption の上に積んでみる。
type StateTReaderTOption[C, S, A] = StateT[({type l[X] = ReaderTOption[C, X]})#l, S, A]
object StateTReaderTOption {
def state[C, S, A](f: S => (S, A)): StateTReaderTOption[C, S, A] =
StateT[({type l[X] = ReaderTOption[C, X]})#l, S, A] {
s: S => Monad[({type l[X] = ReaderTOption[C, X]})#l].pure(f(s))
}
def get[C, S]: StateTReaderTOption[C, S, S] =
state { s => (s, s) }
def put[C, S](s: S): StateTReaderTOption[C, S, Unit] =
state { _ => (s, ()) }
def ro[C, S, A](f: C => Option[A]): StateTReaderTOption[C, S, A] =
StateT[({type l[X] = ReaderTOption[C, X]})#l, S, A] {
s: S =>
ReaderTOption.ro[C, (S, A)]{
c: C => f(c) map {(s, _)}
}
}
}
これは分かりづらいので、分解してみよう。
結局の所 State データ型は S => (S, A) をラッピングするものだから、state のパラメータ名はそれに合わせた。
次に、ReaderTOption のカインドを * -> * (ただ 1つのパラメータを受け取る型コンストラクタ) に変える。
同様に、このデータ型を ReaderTOption として使う方法が必要なので、それは ro に渡される C => Option[A] として表した。
これで Stack を実装することができる。今回は String を使ってみよう。
type Stack = List[String]
{
val pop = StateTReaderTOption.state[Config, Stack, String] {
case x :: xs => (xs, x)
case _ => ???
}
}
pop と push を get と push プリミティブを使って書くこともできる:
import StateTReaderTOption.{get, put}
val pop: StateTReaderTOption[Config, Stack, String] =
for {
s <- get[Config, Stack]
(x :: xs) = s
_ <- put(xs)
} yield x
// pop: StateTReaderTOption[Config, Stack, String] = cats.data.IndexedStateT@b5a4756
def push(x: String): StateTReaderTOption[Config, Stack, Unit] =
for {
xs <- get[Config, Stack]
r <- put(x :: xs)
} yield r
ついでに stackManip も移植する:
def stackManip: StateTReaderTOption[Config, Stack, String] =
for {
_ <- push("Fredo")
a <- pop
b <- pop
} yield(b)
実行してみよう。
stackManip.run(List("Hyman Roth")).run(dummyConfig)
// res3: Option[(Stack, String)] = Some(value = (List(), "Hyman Roth"))
とりあえず State 版と同じ機能までたどりつけた。
次に、Users を StateTReaderTOption.ro を使うように書き換える:
trait Users {
def getUser[S](id: Long): StateTReaderTOption[Config, S, User] =
StateTReaderTOption.ro[Config, S, User] {
case config => config.userRepo.get(id)
}
def findUser[S](name: String): StateTReaderTOption[Config, S, User] =
StateTReaderTOption.ro[Config, S, User] {
case config => config.userRepo.find(name)
}
}
これを使ってリードオンリーの設定を使ったスタックの操作ができるようになった:
trait Program extends Users {
def stackManip: StateTReaderTOption[Config, Stack, Unit] =
for {
u <- getUser(2)
a <- push(u.name)
} yield(a)
}
object Main extends Program {
def run(s: Stack, config: Config): Option[(Stack, Unit)] =
stackManip.run(s).run(config)
}
このプログラムはこのように実行できる:
Main.run(List("Hyman Roth"), dummyConfig)
// res4: Option[(Stack, Unit)] = Some(
// value = (List("Fredo", "Hyman Roth"), ())
// )
これで StateT、ReaderT、それと Option を同時に動かすことができた。
僕が使い方を良く分かってないせいかもしれないが、StateTReaderTOption に関して state や ro
のようなモナド・コンストラクタを書き出すのは頭をひねる難問だった。
プリミティブなモナド値さえ構築できてしまえば、実際の使う側のコード (stackManip などは) 比較的クリーンだと言える。
Cake パターンは確かに回避してるけども、コード中に積み上げられたモナド型である StateTReaderTOption が散らばっている設計になっている。
最終目的として getUser(id: Long) と push などを同時に使いたいというだけの話なら、
8日目に見た自由モナドを使うことで、これらをコマンドとして持つ DSL を構築することも代替案として考えられる。
Future と Either の積み上げ
モナド変換子の用例として度々取り上げられるものに Future データ型と Either の積み上げがある。
日本語で書かれたブログ記事として吉田さん (@xuwei_k) の
Scala で Future と Either を組み合わせたときに綺麗に書く方法というものがある。
東京の外だとあまり知られていない話だと思うが、吉田さんは書道科専攻で、大学では篆書を書いたり判子を刻って (ほる? 何故か変換できない) いたらしい:
「大学では、はんこを刻ったり、篆書を書いてました」
「えっ?なぜプログラマに???」 pic.twitter.com/DEhqy4ELpF
— Kenji Yoshida (@xuwei_k) October 21, 2013ハンドル名の由来となっている徐渭は明代の書・画・詩・詞・戯曲・散文の士で自由奔放な作風で有名だった。 これは吉田さんの関数型言語という書だ。
それはさておき、Future と Either を積み上げる必要が何故あるのだろうか?
ブログ記事によるとこういう説明になっている:
Future[A]は Scala によく現れる。- future をブロックしたくないため、そこらじゅう
Futureだらけになる。 Futureは非同期であるため、発生したエラーを捕獲する必要がある。FutureはThrowableは処理できるが、それに限られている。- プログラムが複雑になってくると、エラー状態に対して自分で型付けしたくなってくる。
FutureとEitherを組み合わせるには?
ここからが準備段階となる:
case class User(id: Long, name: String)
// In actual code, probably more than 2 errors
sealed trait Error
object Error {
final case class UserNotFound(userId: Long) extends Error
final case class ConnectionError(message: String) extends Error
}
object UserRepo {
def followers(userId: Long): Either[Error, List[User]] = ???
}
import UserRepo.followers
user がいて、twitter のようにフォローできて、「フォローしてる」「フォローされてる」という関係を保持するアプリを作るとします。
とりあえず今あるのは、followers という、指定された userId の follower 一覧を取ってくるメソッドです。 さて、このメソッドだけがあったときに 「あるユーザー同士が、相互フォローの関係かどうか?」 を取得するメソッドはどう書けばよいでしょうか?
答えも載っているので、そのまま REPL に書き出してみる。UserId 型だけは Long に変えた。
def isFriends0(user1: Long, user2: Long): Either[Error, Boolean] =
for {
a <- followers(user1).right
b <- followers(user2).right
} yield a.exists(_.id == user2) && b.exists(_.id == user1)
次に、データベース・アクセスか何かを非同期にするために followers が Future を返すようにする:
import scala.concurrent.{ Future, ExecutionContext }
object UserRepo {
def followers(userId: Long): Future[Either[Error, List[User]]] = ???
}
import UserRepo.followers
さてそうしたときに、isFriendsメソッドは、どのように書き換えればいいでしょうか?さて、これもすぐに正解だしてしまいます。 ただ、一応2パターンくらい出しておきましょう
def isFriends1(user1: Long, user2: Long)
(implicit ec: ExecutionContext): Future[Either[Error, Boolean]] =
for {
a <- followers(user1)
b <- followers(user2)
} yield for {
x <- a.right
y <- b.right
} yield x.exists(_.id == user2) && y.exists(_.id == user1)
次のがこれ:
def isFriends2(user1: Long, user2: Long)
(implicit ec: ExecutionContext): Future[Either[Error, Boolean]] =
followers(user1) flatMap {
case Right(a) =>
followers(user2) map {
case Right(b) =>
Right(a.exists(_.id == user2) && b.exists(_.id == user1))
case Left(e) =>
Left(e)
}
case Left(e) =>
Future.successful(Left(e))
}
これらの2つのバージョンの違いは何だろうか?
正常系の場合の動作は同じですが、
followers(user1)がエラーだった場合の動作が異なります。上記の
for式を2回使ってるisFriends1のほうでは、followers(user1)がエラーでも、followers(user2)の呼び出しは必ず実行されます。一方、
isFriends2のほうは、followers(user1)の呼び出しがエラーだと、followers(user2)は実行されません。
どちらにせよ、両方の関数も元のものに比べると入り組んだものとなった。
しかも増えた部分のコードは紋切型 (ボイラープレート) な型合わせをしているのがほとんどだ。
Future[Either[Error, A]] が出てくる全ての関数をこのように書き換えるのは想像したくない。
EitherT データ型
Either のモナド変換子版である EitherT データ型というものがある。
/**
* Transformer for `Either`, allowing the effect of an arbitrary type constructor `F` to be combined with the
* fail-fast effect of `Either`.
*
* `EitherT[F, A, B]` wraps a value of type `F[Either[A, B]]`. An `F[C]` can be lifted in to `EitherT[F, A, C]` via `EitherT.right`,
* and lifted in to a `EitherT[F, C, B]` via `EitherT.left`.
*/
case class EitherT[F[_], A, B](value: F[Either[A, B]]) {
....
}
UserRepo.followers を仮実装してみると、こうなった:
import cats._, cats.data._, cats.syntax.all._
object UserRepo {
def followers(userId: Long)
(implicit ec: ExecutionContext): EitherT[Future, Error, List[User]] =
userId match {
case 0L =>
EitherT.right(Future { List(User(1, "Michael")) })
case 1L =>
EitherT.right(Future { List(User(0, "Vito")) })
case x =>
println("not found")
EitherT.left(Future.successful { Error.UserNotFound(x) })
}
}
import UserRepo.followers
isFriends0 の書き換えをもう一度やってみる。
def isFriends3(user1: Long, user2: Long)
(implicit ec: ExecutionContext): EitherT[Future, Error, Boolean] =
for{
a <- followers(user1)
b <- followers(user2)
} yield a.exists(_.id == user2) && b.exists(_.id == user1)
素晴らしくないだろうか? 型シグネチャを変えて、あと ExecutionContext を受け取るようしたこと以外は、
isFriends3 は isFriends0 と同一のものだ。
実際に使ってみよう。
{
implicit val ec = scala.concurrent.ExecutionContext.global
import scala.concurrent.Await
import scala.concurrent.duration._
Await.result(isFriends3(0, 1).value, 1 second)
}
// res2: Either[Error, Boolean] = Right(value = true)
最初のユーザが見つからない場合は、EitherT はショートするようになっている。
{
implicit val ec = scala.concurrent.ExecutionContext.global
import scala.concurrent.Await
import scala.concurrent.duration._
Await.result(isFriends3(2, 3).value, 1 second)
}
// not found
// res3: Either[Error, Boolean] = Left(value = UserNotFound(userId = 2L))
"not found" は一回しか表示されなかった。
StateTReaderTOption の例と違って、この XorT は様々な場面で活躍しそうな雰囲気だ。
今日はこれまで。
11日目
10日目はモナド変換子という考えを、まず
Kliesli を ReaderT として使って、
次に、Future と Either の積み上げを例にみた。
ジェネリシティ
大局的に見ると、関数型プログラミングは色々なものの抽象化だと考えることができる。 Jeremy Gibbons さんの 2006年の本 Datatype-Generic Programming を流し読みしていると、まとめ的なものが見つかった。
以下は拙訳。
ジェネリック・プログラミングとは、安全性を犠牲にせずにプログラミング言語をより柔軟にすることだ。
値によるジェネリシティ
全てのプログラマが最初に習うことの一つで、最も重要なテクニックは値をパラメータ化することだ。
def triangle4: Unit = {
println("*")
println("**")
println("***")
println("****")
}
4 を抽象化して、パラメータとして追い出すことができる:
def triangle(side: Int): Unit = {
(1 to side) foreach { row =>
(1 to row) foreach { col =>
println("*")
}
}
}
型によるジェネリシティ
List[A] は、要素の型という別の型によってパラメータ化されている
多相的なデータ型 (polymorphic datatype) だ。
これはパラメトリックな多相性 (parametric polymorphism) を可能とする。
def head[A](xs: List[A]): A = xs(0)
上の関数は全てのプロパー型に対して動作する。
関数によるジェネリシティ
高階なプログラムは別のプログラムによりパラメータ化されている。
例えば、foldLeft を使って 2つのリストの追加である append を書くことができる:
def append[A](list: List[A], ys: List[A]): List[A] =
list.foldLeft(ys) { (acc, x) => x :: acc }
append(List(1, 2, 3), List(4, 5, 6))
// res0: List[Int] = List(3, 2, 1, 4, 5, 6)
数を足し合わせるのにも使うことができる:
def sum(list: List[Int]): Int =
list.foldLeft(0) { _ + _ }
構造によるジェネリシティ
Scala Collection のようなコレクション・ライブラリによって体現化される「ジェネリック・プログラミング」がこれだ。 C++ の Standard Template Library の場合は、パラメトリックなデータ型はコンテナとよばれ、 input iterator や forward iterator といったイテレータによって様々な抽象化が提供される。
型クラスという概念もここに当てはまる。
trait Read[A] {
def reads(s: String): Option[A]
}
object Read extends ReadInstances {
def read[A](f: String => Option[A]): Read[A] = new Read[A] {
def reads(s: String): Option[A] = f(s)
}
def apply[A: Read]: Read[A] = implicitly[Read[A]]
}
trait ReadInstances {
implicit lazy val stringRead: Read[String] =
Read.read[String] { Some(_) }
implicit lazy val intRead: Read[Int] =
Read.read[Int] { s =>
try {
Some(s.toInt)
} catch {
case e: NumberFormatException => None
}
}
}
Read[Int].reads("1")
// res1: Option[Int] = Some(value = 1)
型クラスは、型クラス・コントラクトとよばれる型が満たさなければいけない要請を表す。
また、型クラスのインスタンスを定義することで、それらの要請を提供する型を列挙することができる。
Read[A] における A は全称的 (universal) ではないため、
これはアドホック多相性を可能とする。
性質によるジェネリシティ
Scala Collection ライブラリの中では、型が列挙する演算よりも込み入った概念が約束されていることがある。
演算のシグネチャの他にも、 これらの演算が満たす法則や、演算の計算量や空間量に対する漸近的複雑度など、機能以外の特性などがある。
法則を持つ型クラスもここに当てはまる。例えば、Monoid[A] にはモノイド則がある。
それぞれのインスタンスに対して、これらの法則を満たしているかプロパティ・ベース・テストのツールなどを使って検証する必要がある。
ステージによるジェネリシティ
様々な種類のメタプログラミングは、別のプログラムを構築したり操作するプログラムの開発だと考えることができる。 これにはコード生成やマクロも含む。
形によるジェネリシティ
ここに多相的なデータ型である二分木があるとする:
sealed trait Btree[A]
object Btree {
case class Tip[A](a: A) extends Btree[A]
case class Bin[A](left: Btree[A], right: Btree[A]) extends Btree[A]
}
次に、似たようなプログラムを抽象化するために foldB を書いてみる:
def foldB[A, B](tree: Btree[A], b: (B, B) => B)(t: A => B): B =
tree match {
case Btree.Tip(a) => t(a)
case Btree.Bin(xs, ys) => b(foldB(xs, b)(t), foldB(ys, b)(t))
}
次の目標は foldB と foldLeft を抽象化することだ。
これらの 2つの畳み込み演算で異なるのは、それらが作用するデータ型の形 (shape) であって、 それがプログラムそのものの形を変えている。 ここで求めれるパラメータ化の対象はこの形、つまりデータ型やそれらの (
ListやTree) といったコンストラクタをパラメータ化する必要がある。 これをデータ型ジェネリシティ (datatype genericity) とよぶ。
例えば、fold は以下のように表現できるらしい。
import cats._, cats.data._, cats.syntax.all._
trait Fix[F[_,_], A]
def cata[S[_,_]: Bifunctor, A, B](t: Fix[S, A])(f: S[A, B] => B): B = ???
上の例では、S はデータ型の形を表す。
形を抽象化することで、パラメトリックにデータ型ジェネリックなプログラムを書くことができる。
これについては後ほど。
その振る舞いにおいて何らかの方法で形を利用するプログラムはアドホックなデータ型ジェネリックとよぶ。 pretty printer やシリアライザが典型的な例だ。
この例に当てはまりそうなのは Scala Pickling だ。 Pickling はよくある型には予め pickler を提供して、 マクロを使って異なる形に対して pickler のインスタンスを導出している。
この方法のデータ型ジェネリシティは polytypism、 構造的多相性、typecase など様々な名前でよばれ、 Generic Haskell チームが「ジェネリック・プログラミング」と言うときもこの意味だ。….
我々は、パラメトリックなデータ型ジェネリシティこそが「最高基準」であると考え、 講義ノートでも今後は可能な限りパラメトリックなデータ型ジェネリシティに焦点を置く。
Scala 界隈だと、shapeless が形の抽象化に焦点を置いているだろう。
Bifunctor を用いたデータ型ジェネリック・プログラミング
Datatype-Generic Programming の 3.6節「データ型ジェネリシティ」をみてみよう。 Gibbons さんはこれをオリガミ・プログラミングと命名しようとしたみたいだけど、 名前として流行っている気配が無いのでここではデータ型ジェネリック・プログラミングと呼ぶことにする。
既に述べたように、データ構造はプログラム構造を規定する。 そのため、決め手となる形を抽象化して、異なる形のプログラムの共通部分だけのこすというのは理にかなっている。
ListやTreeといったデータ型に共通しているのはそれらが再帰的、つまりFixであることだ。
data Fix s a = In {out :: s a (Fix s a)}
以下は
Fixを異なる形に用いた例だ: リスト、既に見たラベルを内部に持つ二分木、そしてラベルを外部に持つ二分木だ。
data ListF a b = NilF | ConsF a b
type List a = Fix ListF a
data TreeF a b = EmptyF | NodeF a b b
type Tree a = Fix TreeF a
data BtreeF a b = TipF a | BinF b b
type Btree a = Fix BtreeF a
8日目の Why free monads matter
からこれは実は Free データ型であることが分かっているけども、
Functor などに関する意味が異なるので、一から実装してみる:
sealed abstract class Fix[S[_], A] extends Serializable {
def out: S[Fix[S, A]]
}
object Fix {
case class In[S[_], A](out: S[Fix[S, A]]) extends Fix[S, A]
}
Free に倣って、S[_] を左側に、A を右側に置く。
List をまず実装してみる。
sealed trait ListF[+Next, +A]
object ListF {
case class NilF() extends ListF[Nothing, Nothing]
case class ConsF[A, Next](a: A, n: Next) extends ListF[Next, A]
}
type GenericList[A] = Fix[ListF[+*, A], A]
object GenericList {
def nil[A]: GenericList[A] = Fix.In[ListF[+*, A], A](ListF.NilF())
def cons[A](a: A, xs: GenericList[A]): GenericList[A] =
Fix.In[ListF[+*, A], A](ListF.ConsF(a, xs))
}
import GenericList.{ cons, nil }
このように使うことができる:
cons(1, nil)
// res0: GenericList[Int] = In(out = ConsF(a = 1, n = In(out = NilF())))
ここまでは自由モナドで見たのと似ている。
Bifunctor
全ての二項型コンストラクタが不動点化できるとは限らず、 パラメータが反変 (contravariant) な位置 (ソース側) だと問題となる。 全ての要素を「探しだす」ことができる bimap 演算をサポートする (共変な) 双函手 (bifunctor) だとうまくいくことが分かっている。
Cats はこれを Bifunctor とよんでいる:
/**
* A typeclass of types which give rise to two independent, covariant
* functors.
*/
trait Bifunctor[F[_, _]] extends Serializable { self =>
/**
* The quintessential method of the Bifunctor trait, it applies a
* function to each "side" of the bifunctor.
*/
def bimap[A, B, C, D](fab: F[A, B])(f: A => C, g: B => D): F[C, D]
....
}
これが、GenericList の Bifunctor インスタンスだ。
import cats._, cats.data._, cats.syntax.all._
implicit val listFBifunctor: Bifunctor[ListF] = new Bifunctor[ListF] {
def bimap[S1, A1, S2, A2](fab: ListF[S1, A1])(f: S1 => S2, g: A1 => A2): ListF[S2, A2] =
fab match {
case ListF.NilF() => ListF.NilF()
case ListF.ConsF(a, next) => ListF.ConsF(g(a), f(next))
}
}
// listFBifunctor: Bifunctor[ListF] = repl.MdocSession1@2735bff6
Bifunctor からの map の導出
Bifunctorクラスは、様々な再帰パターンをデータ型ジェネリックなプログラムとして表すのに十分な柔軟性を持っていることがわかった。
まず、bimap を使って map を実装する。
object DGP {
def map[F[_, _]: Bifunctor, A1, A2](fa: Fix[F[*, A1], A1])(f: A1 => A2): Fix[F[*, A2], A2] =
Fix.In[F[*, A2], A2](Bifunctor[F].bimap(fa.out)(map(_)(f), f))
}
DGP.map(cons(1, nil)) { _ + 1 }
// res1: Fix[ListF[α4, Int], Int] = In(
// out = ConsF(a = 2, n = In(out = NilF()))
// )
上の map の定義は GenericList から独立しているもので、
Bifunctor と Fix によって抽象化されている。
別の見方をすると、Bifunctor と Fix から Functor をただでもらえると言える。
trait FixInstances {
implicit def fixFunctor[F[_, _]: Bifunctor]: Functor[Lambda[L => Fix[F[*, L], L]]] =
new Functor[Lambda[L => Fix[F[*, L], L]]] {
def map[A1, A2](fa: Fix[F[*, A1], A1])(f: A1 => A2): Fix[F[*, A2], A2] =
Fix.In[F[*, A2], A2](Bifunctor[F].bimap(fa.out)(map(_)(f), f))
}
}
{
val instances = new FixInstances {}
import instances._
import cats.syntax.functor._
cons(1, nil) map { _ + 1 }
}
// res2: GenericList[Int] = In(out = ConsF(a = 2, n = In(out = NilF())))
激しい量の型ラムダだけども、DB.map から Functor インスタンスへと翻訳しただけだというのは明らかだと思う。
Bifunctor からの fold の導出
fold も実装できる。これは、catamorphism から cata とも呼ばれる。
object DGP {
// catamorphism
def fold[F[_, _]: Bifunctor, A1, A2](fa: Fix[F[*, A1], A1])(f: F[A2, A1] => A2): A2 =
{
val g = (fa1: F[Fix[F[*, A1], A1], A1]) =>
Bifunctor[F].leftMap(fa1) { (fold(_)(f)) }
f(g(fa.out))
}
}
DGP.fold[ListF, Int, Int](cons(2, cons(1, nil))) {
case ListF.NilF() => 0
case ListF.ConsF(x, n) => x + n
}
// res4: Int = 3
Bifunctor からの unfold の導出
unfold演算は、ある値からデータ構造を育てるのに使う。 正確には、これはfold演算の双対だ。
unfold は anamorphism から ana とも呼ばれる。
object DGP {
// catamorphism
def fold[F[_, _]: Bifunctor, A1, A2](fa: Fix[F[*, A1], A1])(f: F[A2, A1] => A2): A2 =
{
val g = (fa1: F[Fix[F[*, A1], A1], A1]) =>
Bifunctor[F].leftMap(fa1) { (fold(_)(f)) }
f(g(fa.out))
}
// anamorphism
def unfold[F[_, _]: Bifunctor, A1, A2](x: A2)(f: A2 => F[A2, A1]): Fix[F[*, A1], A1] =
Fix.In[F[*, A1], A1](Bifunctor[F].leftMap(f(x))(unfold[F, A1, A2](_)(f)))
}
数をカウントダウンしてリストを構築してみる:
def pred(n: Int): GenericList[Int] =
DGP.unfold[ListF, Int, Int](n) {
case 0 => ListF.NilF()
case n => ListF.ConsF(n, n - 1)
}
pred(4)
// res6: GenericList[Int] = In(
// out = ConsF(
// a = 4,
// n = In(
// out = ConsF(
// a = 3,
// n = In(
// out = ConsF(a = 2, n = In(out = ConsF(a = 1, n = In(out = NilF()))))
// )
// )
// )
// )
// )
他にもいくつか導出できるみたいだ。
Tree
データ型ジェネリック・プログラミングの肝は形の抽象化だ。
他のデータ型も定義してみよう。例えば、これは二分木の Tree だ:
sealed trait TreeF[+Next, +A]
object TreeF {
case class EmptyF() extends TreeF[Nothing, Nothing]
case class NodeF[Next, A](a: A, left: Next, right: Next) extends TreeF[Next, A]
}
type Tree[A] = Fix[TreeF[?, A], A]
object Tree {
def empty[A]: Tree[A] =
Fix.In[TreeF[+?, A], A](TreeF.EmptyF())
def node[A, Next](a: A, left: Tree[A], right: Tree[A]): Tree[A] =
Fix.In[TreeF[+?, A], A](TreeF.NodeF(a, left, right))
}
木はこのように作る:
import Tree.{empty,node}
node(2, node(1, empty, empty), empty)
// res7: Tree[Int] = In(
// out = NodeF(
// a = 2,
// left = In(
// out = NodeF(a = 1, left = In(out = EmptyF()), right = In(out = EmptyF()))
// ),
// right = In(out = EmptyF())
// )
// )
あとは Bifunctor のインスタンスだけを定義すればいいはずだ:
implicit val treeFBifunctor: Bifunctor[TreeF] = new Bifunctor[TreeF] {
def bimap[A, B, C, D](fab: TreeF[A, B])(f: A => C, g: B => D): TreeF[C, D] =
fab match {
case TreeF.EmptyF() => TreeF.EmptyF()
case TreeF.NodeF(a, left, right) =>
TreeF.NodeF(g(a), f(left), f(right))
}
}
// treeFBifunctor: Bifunctor[TreeF] = repl.MdocSession7@467e46cb
まず、Functor を試してみる:
{
val instances = new FixInstances {}
import instances._
import cats.syntax.functor._
node(2, node(1, empty, empty), empty) map { _ + 1 }
}
// res8: Tree[Int] = In(
// out = NodeF(
// a = 3,
// left = In(
// out = NodeF(a = 2, left = In(out = EmptyF()), right = In(out = EmptyF()))
// ),
// right = In(out = EmptyF())
// )
// )
うまくいった。次に、畳込み。
def sum(tree: Tree[Int]): Int =
DGP.fold[TreeF, Int, Int](tree) {
case TreeF.EmptyF() => 0
case TreeF.NodeF(a, l, r) => a + l + r
}
sum(node(2, node(1, empty, empty), empty))
// res9: Int = 3
fold もできた。
以下は grow という関数で、これはリストから二分探索木を生成する。
def grow[A: PartialOrder](xs: List[A]): Tree[A] =
DGP.unfold[TreeF, A, List[A]](xs) {
case Nil => TreeF.EmptyF()
case x :: xs =>
import cats.syntax.partialOrder._
TreeF.NodeF(x, xs filter {_ <= x}, xs filter {_ > x})
}
grow(List(3, 1, 4, 2))
// res10: Tree[Int] = In(
// out = NodeF(
// a = 3,
// left = In(
// out = NodeF(
// a = 1,
// left = In(out = EmptyF()),
// right = In(
// out = NodeF(
// a = 2,
// left = In(out = EmptyF()),
// right = In(out = EmptyF())
// )
// )
// )
// ),
// right = In(
// out = NodeF(a = 4, left = In(out = EmptyF()), right = In(out = EmptyF()))
// )
// )
// )
unfold もうまくいったみたいだ。
Scala での DGP に関する詳細は、Oliveira さんと Gibbons さん自身が ここでみた考えや他の概念を Scala に翻訳した Scala for Generic Programmers (2008) とその改定版である Scala for Generic Programmers (2010) を出している。
オリガミ・パターン
次に、Gibbons さんはデザイン・パターンは 「それらの主流なプログラミング言語が表現性の欠けている証拠」だと主張している。 そして、それらのパターンを高階データ型ジェネリックなプログラミングで置き換えることに船舵を切っている。
Const データ型
Datatype-Generic Programming の第5章は 「Iterator パターンの本質」(The Essence of the Iterator pattern) と呼ばれていて、 Gibbons さんと Oliveira さんが 2006年に書いた論文と同じ題名だ。 現在公開されているバージョンの The Essence of the Iterator Pattern は 2009年のものだ。DGP の流れをくんだものとしてこの論文を読むと、その文脈が分かるようになると思う。
この論文の冒頭に出てくる例を Java に翻訳してみた。
public static <E> int loop(Collection<E> coll) {
int n = 0;
for (E elem: coll) {
n = n + 1;
doSomething(elem);
}
return n;
}
EIP:
この loop メソッドや、これに似た反復には、 要素の投射 (mapping)、 そして同時にそれらの要素から得られる何かの累積 (accumulating) という2つの側面があって、両方とも捕捉する必要があることを強調したい。
論文の前半は関数型の反復とアプリカティブ・スタイルに関するリビューとなっている。 アプリカティブ・ファンクターに関しては、3種類のアプリカティブがあるらしい:
- Monadic applicative functors
- Naperian applicative functors
- Monoidal applicative functors
全てのモナドがアプリカティブであることは何回か話した。 Naperian applicative functor は固定された形のデータ構造を zip するものだ。
アプリカティブファンクターは McBride さんと Paterson さんによって idiom と名付けられたため、本人たちがアプリカティブ・ファンクターに改名したにもかかわらず Gibbons さんは論文中で idiomatic と applicative の両方の用語を同じ意味で使っている。
Const データ型を用いた monoidal applicative functors
非モナドな、2つ目の種類のアプリカティブ・ファンクターとして モノイダルな対象を持つ定数ファンクターが挙げられる。
全ての Monoid からアプリカティブ・ファンクターを導出することができる。
pure には empty を使って、ap には |+| を使う。
Const データ型は Cats でも Const と呼ばれている:
/**
* [[Const]] is a phantom type, it does not contain a value of its second type parameter `B`
* [[Const]] can be seen as a type level version of `Function.const[A, B]: A => B => A`
*/
final case class Const[A, B](getConst: A) {
/**
* changes the type of the second type parameter
*/
def retag[C]: Const[A, C] =
this.asInstanceOf[Const[A, C]]
....
}
上のコードの型パラメータ A は値を表すが、
B は Functor の型合わせのみに使われる phantom 型だ。
import cats._, cats.data._, cats.syntax.all._
Const(1) map { (_: String) + "!" }
// res0: Const[Int, String] = Const(getConst = 1)
A が Semigroup を形成するとき、Apply を導き出すことができ、
A が Monoid を形成するとき、Applicative を導き出すことができる。
このアプリカティブ・ファンクター間での計算は何らかの結果を累積する。 整数と加算のモノイドの場合は、カウントや和となる…
Const(2).retag[String => String] ap Const(1).retag[String]
// res1: Const[Int, String] = Const(getConst = 3)
アプリカティブ・ファンクターの組み合わせ
EIP:
モナド同様に、アプリカティブ・ファンクターは積 (product) に関して閉じているため、 2つの独立したアプリカティブな効果を積という 1つのものに融合することができ。
Cats はファンクターの積を全く持っていないみたいだ。
ファンクターの積
(ここで書いた実装は #388 で Cats に取り込まれ、後日 Tuple2K となった。)
/**
* [[Tuple2K]] is a product to two independent functor values.
*
* See: [[https://www.cs.ox.ac.uk/jeremy.gibbons/publications/iterator.pdf The Essence of the Iterator Pattern]]
*/
final case class Tuple2K[F[_], G[_], A](first: F[A], second: G[A]) {
/**
* Modify the context `G` of `second` using transformation `f`.
*/
def mapK[H[_]](f: G ~> H): Tuple2K[F, H, A] =
Tuple2K(first, f(second))
}
まずは Functor の積から始める:
private[data] sealed abstract class Tuple2KInstances8 {
implicit def catsDataFunctorForTuple2K[F[_], G[_]](implicit FF: Functor[F], GG: Functor[G]): Functor[λ[α => Tuple2K[F, G, α]]] = new Tuple2KFunctor[F, G] {
def F: Functor[F] = FF
def G: Functor[G] = GG
}
}
private[data] sealed trait Tuple2KFunctor[F[_], G[_]] extends Functor[λ[α => Tuple2K[F, G, α]]] {
def F: Functor[F]
def G: Functor[G]
override def map[A, B](fa: Tuple2K[F, G, A])(f: A => B): Tuple2K[F, G, B] = Tuple2K(F.map(fa.first)(f), G.map(fa.second)(f))
}
使ってみる:
import cats._, cats.data._, cats.syntax.all._
val x = Tuple2K(List(1), 1.some)
// x: Tuple2K[List, Option, Int] = Tuple2K(
// first = List(1),
// second = Some(value = 1)
// )
Functor[Lambda[X => Tuple2K[List, Option, X]]].map(x) { _ + 1 }
// res0: Tuple2K[List[A], Option, Int] = Tuple2K(
// first = List(2),
// second = Some(value = 2)
// )
まず、ペアのようなデータ型 Tuple2K を定義して、型クラスインスタンスの積を表す。
両方に関数 f を渡すことで、簡単に Tuple2K[F, G] に関する Functor を形成することができる
(ただし F、G ともに Functor)。
動作を確かめるために x を写像して、1 を加算してみる。
使用する側のコードをもっときれいにすることができると思うけど、
今の所はこれで良しとする。
Apply ファンクターの積
次は Apply:
private[data] sealed abstract class Tuple2KInstances6 extends Tuple2KInstances7 {
implicit def catsDataApplyForTuple2K[F[_], G[_]](implicit FF: Apply[F], GG: Apply[G]): Apply[λ[α => Tuple2K[F, G, α]]] = new Tuple2KApply[F, G] {
def F: Apply[F] = FF
def G: Apply[G] = GG
}
}
private[data] sealed trait Tuple2KApply[F[_], G[_]] extends Apply[λ[α => Tuple2K[F, G, α]]] with Tuple2KFunctor[F, G] {
def F: Apply[F]
def G: Apply[G]
....
}
これが用例:
{
val x = Tuple2K(List(1), (Some(1): Option[Int]))
val f = Tuple2K(List((_: Int) + 1), (Some((_: Int) * 3): Option[Int => Int]))
Apply[Lambda[X => Tuple2K[List, Option, X]]].ap(f)(x)
}
// res1: Tuple2K[List[A], Option, Int] = Tuple2K(
// first = List(2),
// second = Some(value = 3)
// )
Apply の積は左右で別の関数を渡している。
アプリカティブ・ファンクターの積
最後に、Applicative の積が実装できるようになった:
private[data] sealed abstract class Tuple2KInstances5 extends Tuple2KInstances6 {
implicit def catsDataApplicativeForTuple2K[F[_], G[_]](implicit FF: Applicative[F], GG: Applicative[G]): Applicative[λ[α => Tuple2K[F, G, α]]] = new Tuple2KApplicative[F, G] {
def F: Applicative[F] = FF
def G: Applicative[G] = GG
}
}
private[data] sealed trait Tuple2KApplicative[F[_], G[_]] extends Applicative[λ[α => Tuple2K[F, G, α]]] with Tuple2KApply[F, G] {
def F: Applicative[F]
def G: Applicative[G]
def pure[A](a: A): Tuple2K[F, G, A] = Tuple2K(F.pure(a), G.pure(a))
}
簡単な用例:
Applicative[Lambda[X => Tuple2K[List, Option, X]]].pure(1)
// res2: Tuple2K[List[A], Option, Int] = Tuple2K(
// first = List(1),
// second = Some(value = 1)
// )
pure(1) を呼び出すことで Tuple2K(List(1), Some(1)) を生成することができた。
Applicative の合成
モナド一般では成り立たないが、アプリカティブ・ファンクターは合成に関しても閉じている。 そのため、逐次的に依存したアプリカティブな効果は、合成として融合することができる。
幸いなことに Cats は Applicative の合成は元から入っている。
型クラスインスタンスに compose メソッドが入っている:
@typeclass trait Applicative[F[_]] extends Apply[F] { self =>
/**
* `pure` lifts any value into the Applicative Functor
*
* Applicative[Option].pure(10) = Some(10)
*/
def pure[A](x: A): F[A]
/**
* Two sequentially dependent Applicatives can be composed.
*
* The composition of Applicatives `F` and `G`, `F[G[x]]`, is also an Applicative
*
* Applicative[Option].compose[List].pure(10) = Some(List(10))
*/
def compose[G[_]](implicit GG : Applicative[G]): Applicative[λ[α => F[G[α]]]] =
new CompositeApplicative[F,G] {
implicit def F: Applicative[F] = self
implicit def G: Applicative[G] = GG
}
....
}
使ってみよう。
Applicative[List].compose[Option].pure(1)
// res3: List[Option[Int]] = List(Some(value = 1))
断然使い勝手が良い。
アプリカティブ関数の積
Gibbons さんは、ここでアプリカティブ関数を合成する演算子も紹介しているのだけど、
何故かその点は忘れられることが多い気がする。
アプリカティブ関数とは、A => F[B] の形を取る関数で F が Applicative を形成するものを言う。
Kleisli 合成に似ているが、より良いものだ。
その理由を説明する。
Kliesli 合成は andThen を使って A => F[B] と B => F[C] を合成することができるが、
F は一定であることに注目してほしい。
一方、AppFunc は A => F[B] と B => G[C] を合成することができる。
/**
* [[Func]] is a function `A => F[B]`.
*
* See: [[https://www.cs.ox.ac.uk/jeremy.gibbons/publications/iterator.pdf The Essence of the Iterator Pattern]]
*/
sealed abstract class Func[F[_], A, B] { self =>
def run: A => F[B]
def map[C](f: B => C)(implicit FF: Functor[F]): Func[F, A, C] =
Func.func(a => FF.map(self.run(a))(f))
}
object Func extends FuncInstances {
/** function `A => F[B]. */
def func[F[_], A, B](run0: A => F[B]): Func[F, A, B] =
new Func[F, A, B] {
def run: A => F[B] = run0
}
/** applicative function. */
def appFunc[F[_], A, B](run0: A => F[B])(implicit FF: Applicative[F]): AppFunc[F, A, B] =
new AppFunc[F, A, B] {
def F: Applicative[F] = FF
def run: A => F[B] = run0
}
}
....
/**
* An implementation of [[Func]] that's specialized to [[Applicative]].
*/
sealed abstract class AppFunc[F[_], A, B] extends Func[F, A, B] { self =>
def F: Applicative[F]
def product[G[_]](g: AppFunc[G, A, B]): AppFunc[Lambda[X => Prod[F, G, X]], A, B] =
{
implicit val FF: Applicative[F] = self.F
implicit val GG: Applicative[G] = g.F
Func.appFunc[Lambda[X => Prod[F, G, X]], A, B]{
a: A => Prod(self.run(a), g.run(a))
}
}
....
}
使ってみる:
{
val f = Func.appFunc { x: Int => List(x.toString + "!") }
val g = Func.appFunc { x: Int => (Some(x.toString + "?"): Option[String]) }
val h = f product g
h.run(1)
}
// res4: Tuple2K[List, Option[A], String] = Tuple2K(
// first = List("1!"),
// second = Some(value = "1?")
// )
2つのアプリカティブ・ファンクターが並んで実行されているのが分かると思う。
アプリカティブ関数の合成
これが andThen と compose:
def compose[G[_], C](g: AppFunc[G, C, A]): AppFunc[Lambda[X => G[F[X]]], C, B] =
{
implicit val FF: Applicative[F] = self.F
implicit val GG: Applicative[G] = g.F
implicit val GGFF: Applicative[Lambda[X => G[F[X]]]] = GG.compose(FF)
Func.appFunc[Lambda[X => G[F[X]]], C, B]({
c: C => GG.map(g.run(c))(self.run)
})
}
def andThen[G[_], C](g: AppFunc[G, B, C]): AppFunc[Lambda[X => F[G[X]]], A, C] =
g.compose(self)
{
val f = Func.appFunc { x: Int => List(x.toString + "!") }
val g = Func.appFunc { x: String => (Some(x + "?"): Option[String]) }
val h = f andThen g
h.run(1)
}
// res5: Nested[List, Option[A], String] = Nested(
// value = List(Some(value = "1!?"))
// )
EIP:
これらの 2つの演算子はアプリカティブ計算を2つの異なる方法で組み合わせる。 これらをそれぞれ並行合成、逐次合成と呼ぶ。
アプリカティブ計算の組み合わせは Applicative の全てに適用できる抽象的な概念だ。続きはまた後で。
12日目
11日目は、Jeremy Gibbons さんの
Datatype-Generic Programming を読み始めて、
Fix と Bifunctor の巧妙な使い方をみた。
次に「Iterator パターンの本質」(The Essence of the Iterator Pattern) に進み、
Cats が Const を使って Int のようなモノイダル・アプリカティブを表していること、
アプリカティブ関数を合成する方法を欠いていることが分かった。
F[A] と G[A] のペアを表すデータ型である Tuple2K の実装を始め、
アプリカティブ関数を表す AppFunc も実装した。
#388
Traverse
The Essence of the Iterator Pattern:
McBride と Paterson がアプリカティブ計算の動機として例に挙げた 3つの例のうち、 2つ (モナディックな作用のリストの sequence と、行列の転置) は traversal と呼ばれる一般スキームの例だ。 これは、
mapのようにデータ構造内の要素の反復することを伴うが、 ただし、ある特定の関数適用をアプリカティブに解釈する。これは Traversable なデータ構造という型クラスとして表現される。
Cats では、この型クラスは Traverse と呼ばれる:
@typeclass trait Traverse[F[_]] extends Functor[F] with Foldable[F] { self =>
/**
* given a function which returns a G effect, thread this effect
* through the running of this function on all the values in F,
* returning an F[A] in a G context
*/
def traverse[G[_]: Applicative, A, B](fa: F[A])(f: A => G[B]): G[F[B]]
/**
* thread all the G effects through the F structure to invert the
* structure from F[G[_]] to G[F[_]]
*/
def sequence[G[_]: Applicative, A](fga: F[G[A]]): G[F[A]] =
traverse(fga)(ga => ga)
....
}
f が A => G[B] という形を取ることに注目してほしい。
m が恒等アプリカティブ・ファンクターであるとき、 traversal はリストのファンクター的な
mapと一致する (ラッパーを無視すると)。
Cats に恒等アプリカティブ・ファンクターは以下のように定義されている:
type Id[A] = A
implicit val Id: Bimonad[Id] =
new Bimonad[Id] {
def pure[A](a: A): A = a
def extract[A](a: A): A = a
def flatMap[A, B](a: A)(f: A => B): B = f(a)
def coflatMap[A, B](a: A)(f: A => B): B = f(a)
override def map[A, B](fa: A)(f: A => B): B = f(fa)
override def ap[A, B](fa: A)(ff: A => B): B = ff(fa)
override def flatten[A](ffa: A): A = ffa
override def map2[A, B, Z](fa: A, fb: B)(f: (A, B) => Z): Z = f(fa, fb)
override def lift[A, B](f: A => B): A => B = f
override def imap[A, B](fa: A)(f: A => B)(fi: B => A): B = f(fa)
}
Id を使って、List(1, 2, 3) を走査 (traverse) してみる。
import cats._, cats.data._, cats.syntax.all._
List(1, 2, 3) traverse[Id, Int] { (x: Int) => x + 1 }
// res0: Id[List[Int]] = List(2, 3, 4)
モナディックなアプリカティブ・ファンクターの場合、traversal はモナディックな map に特化し、同じ用例となる。 traversal はモナディックな map を少し一般化したものだと考えることができる。
List を使って試してみる:
List(1, 2, 3) traverse { (x: Int) => (Some(x + 1): Option[Int]) }
// res1: Option[List[Int]] = Some(value = List(2, 3, 4))
List(1, 2, 3) traverse { (x: Int) => None }
// res2: Option[List[Nothing]] = None
Naperian なアプリカティブ・ファンクターの場合は、traversal は結果を転置する。
これはパス。
モノイダルなアプリカティブ・ファンクターの場合は、traversal は値を累積する。
reduce関数は各要素に値を割り当てる関数を受け取って、累積する。
def reduce[A, B, F[_]](fa: F[A])(f: A => B)
(implicit FF: Traverse[F], BB: Monoid[B]): B =
{
val g: A => Const[B, Unit] = { (a: A) => Const((f(a))) }
val x = FF.traverse[Const[B, *], A, Unit](fa)(g)
x.getConst
}
これはこのように使う:
reduce(List('a', 'b', 'c')) { c: Char => c.toInt }
// res3: Int = 294
部分的ユニフィケーション (Scala 2.13 ではデフォルト、Scala 2.12 では -Ypartial-unification) のおかげで、traverse は型推論を行うことができる:
def reduce[A, B, F[_]](fa: F[A])(f: A => B)
(implicit FF: Traverse[F], BB: Monoid[B]): B =
{
val x = fa traverse { (a: A) => Const[B, Unit]((f(a))) }
x.getConst
}
これに関してはまた後で。
sequence 関数
Applicative と Traverse は McBride さんと Paterson さんによって
Applicative programming with effects の中でセットで言及されている。
この背景として、数ヶ月前 (2015年3月) まで、Control.Monad パッケージの
sequence 関数は以下のように定義されていた:
-- | Evaluate each action in the sequence from left to right,
-- and collect the results.
sequence :: Monad m => [m a] -> m [a]
これを Scala に翻訳すると、このようになる:
def sequence[G[_]: Monad, A](gas: List[G[A]]): G[List[A]]
これはモナディック値のリストを受け取って、リストのモナディック値を返す。
これだけでも十分便利そうだが、このように List 決め打ちの関数が出てきたら、
何か良い型クラスで置換できないかを疑ってみるべきだ。
McBride さんと Paterson さんは、まず sequence 関数の
Monad を Applicative に置換して、dist として一般化した:
def dist[G[_]: Applicative, A](gas: List[G[A]]): G[List[A]]
次に、dist が map と一緒に呼ばれることが多いことに気付いたので、
アプリカティブ関数をパラメータとして追加して、これを traverse と呼んだ:
def traverse[G[_]: Applicative, A, B](as: List[A])(f: A => G[B]): G[List[B]]
最後に、このシグネチャを型クラスとして一般化したものが Traversible 型クラスと呼ばれるものとなった:
@typeclass trait Traverse[F[_]] extends Functor[F] with Foldable[F] { self =>
/**
* given a function which returns a G effect, thread this effect
* through the running of this function on all the values in F,
* returning an F[A] in a G context
*/
def traverse[G[_]: Applicative, A, B](fa: F[A])(f: A => G[B]): G[F[B]]
/**
* thread all the G effects through the F structure to invert the
* structure from F[G[_]] to G[F[_]]
*/
def sequence[G[_]: Applicative, A](fga: F[G[A]]): G[F[A]] =
traverse(fga)(ga => ga)
....
}
そのため、歴史の必然として Traverse はデータ型ジェネリックな sequence 関数を実装する。
言ってみれば traverse に identity を渡しただけなんだけど、
F[G[A]] を G[F[A]] にひっくり返しただけなので、コンセプトとして覚えやすい。
標準ライブラリの Future に入ってるこの関数として見たことがあるかもしれない。
import scala.concurrent.{ Future, ExecutionContext, Await }
import scala.concurrent.duration._
val x = {
implicit val ec = scala.concurrent.ExecutionContext.global
List(Future { 1 }, Future { 2 }).sequence
}
// x: Future[List[Int]] = Future(Success(List(1, 2)))
Await.result(x, 1 second)
// res5: List[Int] = List(1, 2)
Either の List をまとめて Either にするとか便利かもしれない。
List(Right(1): Either[String, Int]).sequence
// res6: Either[String, List[Int]] = Right(value = List(1))
List(Right(1): Either[String, Int], Left("boom"): Either[String, Int]).sequence
// res7: Either[String, List[Int]] = Left(value = "boom")
sequenceU を使う必要が無くなったことに注意してほしい。
TraverseFilter
/**
* `TraverseFilter`, also known as `Witherable`, represents list-like structures
* that can essentially have a `traverse` and a `filter` applied as a single
* combined operation (`traverseFilter`).
*
* Based on Haskell's [[https://hackage.haskell.org/package/witherable-0.1.3.3/docs/Data-Witherable.html Data.Witherable]]
*/
@typeclass
trait TraverseFilter[F[_]] extends FunctorFilter[F] {
def traverse: Traverse[F]
final override def functor: Functor[F] = traverse
/**
* A combined [[traverse]] and [[filter]]. Filtering is handled via `Option`
* instead of `Boolean` such that the output type `B` can be different than
* the input type `A`.
*
* Example:
* {{{
* scala> import cats.implicits._
* scala> val m: Map[Int, String] = Map(1 -> "one", 3 -> "three")
* scala> val l: List[Int] = List(1, 2, 3, 4)
* scala> def asString(i: Int): Eval[Option[String]] = Now(m.get(i))
* scala> val result: Eval[List[String]] = l.traverseFilter(asString)
* scala> result.value
* res0: List[String] = List(one, three)
* }}}
*/
def traverseFilter[G[_], A, B](fa: F[A])(f: A => G[Option[B]])(implicit G: Applicative[G]): G[F[B]]
def sequenceFilter[G[_], A](fgoa: F[G[Option[A]]])(implicit G: Applicative[G]): G[F[A]] =
traverseFilter(fgoa)(identity)
def filterA[G[_], A](fa: F[A])(f: A => G[Boolean])(implicit G: Applicative[G]): G[F[A]] =
traverseFilter(fa)(a => G.map(f(a))(if (_) Some(a) else None))
def traverseEither[G[_], A, B, E](
fa: F[A]
)(f: A => G[Either[E, B]])(g: (A, E) => G[Unit])(implicit G: Monad[G]): G[F[B]] =
traverseFilter(fa)(a =>
G.flatMap(f(a)) {
case Left(e) => G.as(g(a, e), Option.empty[B])
case Right(b) => G.pure(Some(b))
}
)
override def mapFilter[A, B](fa: F[A])(f: A => Option[B]): F[B] =
traverseFilter[Id, A, B](fa)(f)
/**
* Removes duplicate elements from a list, keeping only the first occurrence.
*/
def ordDistinct[A](fa: F[A])(implicit O: Order[A]): F[A] = {
implicit val ord: Ordering[A] = O.toOrdering
traverseFilter[State[TreeSet[A], *], A, A](fa)(a =>
State(alreadyIn => if (alreadyIn(a)) (alreadyIn, None) else (alreadyIn + a, Some(a)))
)
.run(TreeSet.empty)
.value
._2
}
/**
* Removes duplicate elements from a list, keeping only the first occurrence.
* This is usually faster than ordDistinct, especially for things that have a slow comparion (like String).
*/
def hashDistinct[A](fa: F[A])(implicit H: Hash[A]): F[A] =
traverseFilter[State[HashSet[A], *], A, A](fa)(a =>
State(alreadyIn => if (alreadyIn(a)) (alreadyIn, None) else (alreadyIn + a, Some(a)))
)
.run(HashSet.empty)
.value
._2
}
filterA
filterA は filterM をより一般化 (もしくは弱く) したバージョンで、Monad[G] の代わりに Applicative[G] を要求する。
以下のように使うことができる:
import cats._, cats.syntax.all._
List(1, 2, 3) filterA { x => List(true, false) }
// res0: List[List[Int]] = List(
// List(1, 2, 3),
// List(1, 2),
// List(1, 3),
// List(1),
// List(2, 3),
// List(2),
// List(3),
// List()
// )
Vector(1, 2, 3) filterA { x => Vector(true, false) }
// res1: Vector[Vector[Int]] = Vector(
// Vector(1, 2, 3),
// Vector(1, 2),
// Vector(1, 3),
// Vector(1),
// Vector(2, 3),
// Vector(2),
// Vector(3),
// Vector()
// )
部分的ユニフィケーションを用いた型推論の強制
EIP:
ここではいくつかのデータ型とそれに関連した強要関数 (coercion function)、
Id、unId、Const、unConstが出てくる。 読みやすくするために、これらの強要に共通する記法を導入する。
Scala の場合は implicit と型推論だけで結構いける。 だけど、型クラスを駆使していると Scala の型推論の弱点にも出くわすことがある。 中でも頻繁に遭遇するのは部分適用されたパラメータ型を推論できないという問題で、 SI-2712 として知られている。
これは Miles Sabin さんによって scala#5102 において、”-Ypartial-unification” フラグとして修正された。Explaining Miles’s Magic も参照してほしい。
以下は Daniel さんが用いた例だ:
def foo[F[_], A](fa: F[A]): String = fa.toString
foo { x: Int => x * 2 }
// res0: String = "<function1>"
上の例は以前はコンパイルしなかった。
コンパイルしない理由は
Function1が 2つのパラメータを受け取るのに対して、F[_]は 1つしかパラメータを取らないからだ。
-Ypartial-unification によってコンパイルするようになるが、コンパイラは型コンストラクタが左から右へと部分的に適用可能だという前提で推測を行うことに注意する必要がある。つまり、これは右バイアスのかかった Either のようなデータ型に恩恵があるが、左バイアスのかかったデータ型を使っていると間違った結果が得られる可能性がある。
2019年に Scala 2.13.0 がリリースされ、これは部分的ユニフィケーションがデフォルトで使えるようになった。
形とコンテンツ
EIP:
要素の収集に関してパラメトリックに多相であることの他に、 このジェネリックな
traverse演算はもう 2つの次元によってパラメータ化されている: traverse されるデータ型と、traversal が解釈されるアプリカティブ・ファンクターだ。 後者をモノイドとしてのリストに特化すると、ジェネリックなcontents演算が得られる。
Cats を用いて実装するとこうなる:
import cats._, cats.data._, cats.syntax.all._
def contents[F[_], A](fa: F[A])(implicit FF: Traverse[F]): Const[List[A], F[Unit]] =
{
val contentsBody: A => Const[List[A], Unit] = { (a: A) => Const(List(a)) }
FF.traverse(fa)(contentsBody)
}
これで Traverse をサポートする任意のデータ型から List を得られるようになった。
contents(Vector(1, 2, 3)).getConst
// res0: List[Int] = List(1, 2, 3)
これが逆順になっているのは果たして正しいのか、ちょっと定かではない。
分解の片方は、単純な写像 (map)、つまり恒等アプリカティブ・ファンクターによって解釈される traversal から得ることができる。
恒等アプリカティブ・ファンクターとは Id[_] のことだというのは既にみた通り。
def shape[F[_], A](fa: F[A])(implicit FF: Traverse[F]): Id[F[Unit]] =
{
val shapeBody: A => Id[Unit] = { (a: A) => () }
FF.traverse(fa)(shapeBody)
}
Vector(1, 2, 3) の形はこうなる:
shape(Vector(1, 2, 3))
// res1: Id[Vector[Unit]] = Vector((), (), ())
EIP:
この traversal のペアは、ここで取り上げている反復の 2つの側面、 すなわち写像 (mapping) と累積 (accumulation) を体現するものとなっている。
次に、EIP はアプリカティブ合成を説明するために shape と contents を以下のように組み合わせている:
def decompose[F[_], A](fa: F[A])(implicit FF: Traverse[F]) =
Tuple2K[Const[List[A], *], Id, F[Unit]](contents(fa), shape(fa))
val d = decompose(Vector(1, 2, 3))
// d: Tuple2K[Const[List[Int], β0], Id, Vector[Unit]] = Tuple2K(
// first = Const(getConst = List(1, 2, 3)),
// second = Vector((), (), ())
// )
d.first
// res2: Const[List[Int], Vector[Unit]] = Const(getConst = List(1, 2, 3))
d.second
// res3: Id[Vector[Unit]] = Vector((), (), ())
問題は traverse が 2回走っていることだ。
これら2つの走査 (traversal) を 1つに融合 (fuse) させることはできないだろうか? アプリカティブ・ファンクターの積は正にそのためにある。
これを AppFunc で書いてみよう。
import cats.data.Func.appFunc
def contentsBody[A]: AppFunc[Const[List[A], *], A, Unit] =
appFunc[Const[List[A], *], A, Unit] { (a: A) => Const(List(a)) }
def shapeBody[A]: AppFunc[Id, A, Unit] =
appFunc { (a: A) => ((): Id[Unit]) }
def decompose[F[_], A](fa: F[A])(implicit FF: Traverse[F]) =
(contentsBody[A] product shapeBody[A]).traverse(fa)
val d = decompose(Vector(1, 2, 3))
// d: Tuple2K[Const[List[Int], β1], Id[A], Vector[Unit]] = Tuple2K(
// first = Const(getConst = List(1, 2, 3)),
// second = Vector((), (), ())
// )
d.first
// res5: Const[List[Int], Vector[Unit]] = Const(getConst = List(1, 2, 3))
d.second
// res6: Id[Vector[Unit]] = Vector((), (), ())
decompose の戻り値の型が少しごちゃごちゃしてきたが、AppFunc によって推論されている:
Tuple2K[Const[List[Int], β1], Id[A], Vector[Unit]].
Applicative wordcount
EIP 6節、「アプリカティブ・ファンクターを用いたモジュラー・プログラミング」まで飛ばす。
EIP:
アプリカティブ・ファンクターには他にもモナドに勝る利点があって、 それは複雑な反復をよりシンプルなものからモジュラーに開発できることにある。 ….
Unix でよく使われる wordcount ユーティリティである
wcを例にこれを説明しよう。 `wc` はテキストファイルの文字数、語句数、行数を計算する。
この例は完全にアプリカティブ関数の合成を使って翻訳することができるけども、 この機能は現在私家版のブランチのみで公開されている。 (PR #388 は審査中)
アプリカティブなモジュラー反復
import cats._, cats.data._, cats.syntax.all._
import Func.appFunc
wcプログラムの文字数のカウント部分は「モノイドとしてのInt」のアプリカティブ・ファンクターを累積した結果となる:
以下は Int をモノイダル・アプリカティブとして使うための型エイリアスだ:
type Count[A] = Const[Int, A]
上のコードでは、A は最後まで使われないファントム型なので、Unit に決め打ちしてしまう:
def liftInt(i: Int): Count[Unit] = Const(i)
def count[A](a: A): Count[Unit] = liftInt(1)
この反復の本体は全ての要素に対して 1 を返す:
lazy val countChar: AppFunc[Count, Char, Unit] = appFunc(count)
この AppFunc を使うには、traverse を List[Char] と共に呼び出す。
これは Hamlet から僕が見つけてきた引用だ:
lazy val text = ("Faith, I must leave thee, love, and shortly too.\n" +
"My operant powers their functions leave to do.\n").toList
countChar traverse text
// res0: Count[List[Unit]] = Const(getConst = 96)
うまくいった。
行数のカウント (実際には改行文字のカウントなので、最終行に改行が無いと、それは無視される) も同様だ。 違いは使う数字が違うだけで、それぞれ改行文字ならば 1、それ以外は 0 を返すようにする。
def testIf(b: Boolean): Int = if (b) 1 else 0
lazy val countLine: AppFunc[Count, Char, Unit] =
appFunc { (c: Char) => liftInt(testIf(c === '\n')) }
これも、使うには traverse を呼び出す:
countLine traverse text
// res1: Count[List[Unit]] = Const(getConst = 2)
語句のカウントは、状態が関わってくるため少しトリッキーだ。 ここでは、現在語句内にいるかどうかを表す
Boolean値の状態を使ったStateモナドを使って、 次にそれをカウントするためのアプリカティブ・ファンクターに合成する。
def isSpace(c: Char): Boolean = (c === ' ' || c === '\n' || c === '\t')
lazy val countWord =
appFunc { (c: Char) =>
import cats.data.State.{ get, set }
for {
x <- get[Boolean]
y = !isSpace(c)
_ <- set(y)
} yield testIf(y && !x)
} andThen appFunc(liftInt)
AppFunc を走査するとこれは State データ型が返ってくる:
val x = countWord traverse text
// x: Nested[IndexedStateT[Eval, Boolean, Boolean, A], Count[A], List[Unit]] = Nested(
// value = cats.data.IndexedStateT@63327bc9
// )
この状態機械を初期値 false で実行すると結果が返ってくる:
x.value.runA(false).value
// res2: Count[List[Unit]] = Const(getConst = 17)
17 words だ。
shape と content でやったように、アプリカティブ関数を組み合わせることで走査を 1つに融合 (fuse) できる。
lazy val countAll = countWord
.product(countLine)
.product(countChar)
val allResults = countAll traverse text
// allResults: Tuple2K[Tuple2K[Nested[IndexedStateT[Eval, Boolean, Boolean, A], Count[A], γ3], Count[A], α], Count[A], List[Unit]] = Tuple2K(
// first = Tuple2K(
// first = Nested(value = cats.data.IndexedStateT@211781c8),
// second = Const(getConst = 2)
// ),
// second = Const(getConst = 96)
// )
val charCount = allResults.second
// charCount: Count[List[Unit]] = Const(getConst = 96)
val lineCount = allResults.first.second
// lineCount: Count[List[Unit]] = Const(getConst = 2)
val wordCountState = allResults.first.first
// wordCountState: Nested[IndexedStateT[Eval, Boolean, Boolean, A], Count[A], List[Unit]] = Nested(
// value = cats.data.IndexedStateT@211781c8
// )
val wordCount = wordCountState.value.runA(false).value
// wordCount: Count[List[Unit]] = Const(getConst = 17)
EIP:
アプリカティブ・ファンクターはより豊かな合成演算子を持つため、 多くの場合モナド変換子をリプレースすることができる。 また、アプリカティブはモナド以外の計算も合成できるという利点もある。
今日はここまで。
13日目
12日目は「Iterator パターンの本質」(The Essence of the Iterator Pattern) の続きで、
Traverse、形とコンテンツ、そして applicative wordcount の例題をみた。
Id データ型
EIP を読んでる途中でちらっと Id というものが出てきたけど、面白い道具なので、ちょっとみてみよう。
別名 Identiy、恒等射 (Identity functor)、恒等モナド (Identity monad) など文脈によって色んな名前で出てくる。
このデータ型の定義は非常にシンプルなものだ:
type Id[A] = A
scaladoc と型クラスのインスタンスと一緒だとこうなっている:
/**
* Identity, encoded as `type Id[A] = A`, a convenient alias to make
* identity instances well-kinded.
*
* The identity monad can be seen as the ambient monad that encodes
* the effect of having no effect. It is ambient in the sense that
* plain pure values are values of `Id`.
*
* For instance, the [[cats.Functor]] instance for `[[cats.Id]]`
* allows us to apply a function `A => B` to an `Id[A]` and get an
* `Id[B]`. However, an `Id[A]` is the same as `A`, so all we're doing
* is applying a pure function of type `A => B` to a pure value of
* type `A` to get a pure value of type `B`. That is, the instance
* encodes pure unary function application.
*/
type Id[A] = A
implicit val catsInstancesForId
: Bimonad[Id] with CommutativeMonad[Id] with Comonad[Id] with NonEmptyTraverse[Id] with Distributive[Id] =
new Bimonad[Id] with CommutativeMonad[Id] with Comonad[Id] with NonEmptyTraverse[Id] with Distributive[Id] {
def pure[A](a: A): A = a
def extract[A](a: A): A = a
def flatMap[A, B](a: A)(f: A => B): B = f(a)
def coflatMap[A, B](a: A)(f: A => B): B = f(a)
@tailrec def tailRecM[A, B](a: A)(f: A => Either[A, B]): B =
f(a) match {
case Left(a1) => tailRecM(a1)(f)
case Right(b) => b
}
override def distribute[F[_], A, B](fa: F[A])(f: A => B)(implicit F: Functor[F]): Id[F[B]] = F.map(fa)(f)
override def map[A, B](fa: A)(f: A => B): B = f(fa)
override def ap[A, B](ff: A => B)(fa: A): B = ff(fa)
override def flatten[A](ffa: A): A = ffa
override def map2[A, B, Z](fa: A, fb: B)(f: (A, B) => Z): Z = f(fa, fb)
override def lift[A, B](f: A => B): A => B = f
override def imap[A, B](fa: A)(f: A => B)(fi: B => A): B = f(fa)
def foldLeft[A, B](a: A, b: B)(f: (B, A) => B) = f(b, a)
def foldRight[A, B](a: A, lb: Eval[B])(f: (A, Eval[B]) => Eval[B]): Eval[B] =
f(a, lb)
def nonEmptyTraverse[G[_], A, B](a: A)(f: A => G[B])(implicit G: Apply[G]): G[B] =
f(a)
override def foldMap[A, B](fa: Id[A])(f: A => B)(implicit B: Monoid[B]): B = f(fa)
override def reduce[A](fa: Id[A])(implicit A: Semigroup[A]): A =
fa
def reduceLeftTo[A, B](fa: Id[A])(f: A => B)(g: (B, A) => B): B =
f(fa)
override def reduceLeft[A](fa: Id[A])(f: (A, A) => A): A =
fa
override def reduceLeftToOption[A, B](fa: Id[A])(f: A => B)(g: (B, A) => B): Option[B] =
Some(f(fa))
override def reduceRight[A](fa: Id[A])(f: (A, Eval[A]) => Eval[A]): Eval[A] =
Now(fa)
def reduceRightTo[A, B](fa: Id[A])(f: A => B)(g: (A, Eval[B]) => Eval[B]): Eval[B] =
Now(f(fa))
override def reduceRightToOption[A, B](fa: Id[A])(f: A => B)(g: (A, Eval[B]) => Eval[B]): Eval[Option[B]] =
Now(Some(f(fa)))
override def reduceMap[A, B](fa: Id[A])(f: A => B)(implicit B: Semigroup[B]): B = f(fa)
override def size[A](fa: Id[A]): Long = 1L
override def get[A](fa: Id[A])(idx: Long): Option[A] =
if (idx == 0L) Some(fa) else None
override def isEmpty[A](fa: Id[A]): Boolean = false
}
Id の値はこのように作成する:
import cats._, cats.syntax.all._
val one: Id[Int] = 1
// one: Id[Int] = 1
Functor としての Id
Id の Functor インスタンスは関数の適用と同じだ:
Functor[Id].map(one) { _ + 1 }
// res0: Id[Int] = 2
Apply としての Id
Apply の ap メソッドは Id[A => B] を受け取るが、実際にはただの A => B なので、これも関数適用として実装されている:
Apply[Id].ap({ _ + 1 }: Id[Int => Int])(one)
// res1: Id[Int] = 2
FlatMap としての Id
FlatMap の flatMap メソッドは A => Id[B] も同様。これも関数適用として実装されている:
FlatMap[Id].flatMap(one) { _ + 1 }
// res2: Id[Int] = 2
Id ってなんで嬉しいの?
一見 Id はあんまり便利そうじゃない。ヒントは定義の上にあった Scaladoc にある「恒等インスタンスのカインドを整えるための便利エイリアス」。つまり、なんらかの型 A を F[A] に持ち上げる必要があって、そのときに Id は作用を一切導入せずに使うことができる。あとでその例もみてみる。
Eval データ型
Cats には、Eval という評価を制御するデータ型がある。
sealed abstract class Eval[+A] extends Serializable { self =>
/**
* Evaluate the computation and return an A value.
*
* For lazy instances (Later, Always), any necessary computation
* will be performed at this point. For eager instances (Now), a
* value will be immediately returned.
*/
def value: A
/**
* Ensure that the result of the computation (if any) will be
* memoized.
*
* Practically, this means that when called on an Always[A] a
* Later[A] with an equivalent computation will be returned.
*/
def memoize: Eval[A]
}
Eval 値を作成するにはいくつかの方法がある:
object Eval extends EvalInstances {
/**
* Construct an eager Eval[A] value (i.e. Now[A]).
*/
def now[A](a: A): Eval[A] = Now(a)
/**
* Construct a lazy Eval[A] value with caching (i.e. Later[A]).
*/
def later[A](a: => A): Eval[A] = new Later(a _)
/**
* Construct a lazy Eval[A] value without caching (i.e. Always[A]).
*/
def always[A](a: => A): Eval[A] = new Always(a _)
/**
* Defer a computation which produces an Eval[A] value.
*
* This is useful when you want to delay execution of an expression
* which produces an Eval[A] value. Like .flatMap, it is stack-safe.
*/
def defer[A](a: => Eval[A]): Eval[A] =
new Eval.Call[A](a _) {}
/**
* Static Eval instances for some common values.
*
* These can be useful in cases where the same values may be needed
* many times.
*/
val Unit: Eval[Unit] = Now(())
val True: Eval[Boolean] = Now(true)
val False: Eval[Boolean] = Now(false)
val Zero: Eval[Int] = Now(0)
val One: Eval[Int] = Now(1)
....
}
Eval.later
最も便利なのは、Eval.later で、これは名前渡しのパラメータを lazy val で捕獲している。
import cats._, cats.data._, cats.syntax.all._
var g: Int = 0
// g: Int = 0
val x = Eval.later {
g = g + 1
g
}
// x: Eval[Int] = cats.Later@1db44b96
g = 2
x.value
// res1: Int = 3
x.value
// res2: Int = 3
value はキャッシュされているため、2回目の評価は走らない。
Eval.now
Eval.now は即座に評価され結果はフィールドにて捕獲されるため、これも 2回目の評価は走らない。
val y = Eval.now {
g = g + 1
g
}
// y: Eval[Int] = Now(value = 4)
y.value
// res3: Int = 4
y.value
// res4: Int = 4
Eval.always
Eval.always はキャッシュしない。
val z = Eval.always {
g = g + 1
g
}
// z: Eval[Int] = cats.Always@2d0e17d4
z.value
// res5: Int = 5
z.value
// res6: Int = 6
スタックセーフな遅延演算
Eval の便利な機能は内部でトランポリンを使った map と flatMap により、スタックセーフな遅延演算をサポートすることだ。つまりスタックオーバーフローを回避できる。
また、Eval[A] を返す計算を遅延させるために Eval.defer というものもある。例えば、List の foldRight はそれを使って実装されている:
def foldRight[A, B](fa: List[A], lb: Eval[B])(f: (A, Eval[B]) => Eval[B]): Eval[B] = {
def loop(as: List[A]): Eval[B] =
as match {
case Nil => lb
case h :: t => f(h, Eval.defer(loop(t)))
}
Eval.defer(loop(fa))
}
まずはわざとスタックを溢れさせてみよう:
scala> :paste
object OddEven0 {
def odd(n: Int): String = even(n - 1)
def even(n: Int): String = if (n <= 0) "done" else odd(n - 1)
}
// Exiting paste mode, now interpreting.
defined object OddEven0
scala> OddEven0.even(200000)
java.lang.StackOverflowError
at OddEven0$.even(<console>:15)
at OddEven0$.odd(<console>:14)
at OddEven0$.even(<console>:15)
at OddEven0$.odd(<console>:14)
at OddEven0$.even(<console>:15)
....
安全版を書いてみるとこうなった:
object OddEven1 {
def odd(n: Int): Eval[String] = Eval.defer {even(n - 1)}
def even(n: Int): Eval[String] =
Eval.now { n <= 0 } flatMap {
case true => Eval.now {"done"}
case _ => Eval.defer { odd(n - 1) }
}
}
OddEven1.even(200000).value
// res7: String = "done"
初期の Cats のバージョンだと上のコードでもスタックオーバーフローが発生していたが、David Gregory さんが #769 で修正してくれたので、このままで動作するようになったみたいだ。
抽象的な Future
特に大規模なアプリケーションを構築するという文脈でモナドの強力な応用例として、たまに言及されているブログ記事として抽象的な Future (The Abstract Future) がある。これはもともと Precog 社の開発チームからのブログに 2012年11月27日に Kris Nuttycombe (@nuttycom) さんが投稿したものだ。
Precog 社ではこの Future を多用しており、直接使ったり、Akka のアクターフレームワーク上に実装されたサブシステムと合成可能な方法で会話するための方法として使ったりしている。おそらく Future は今あるツールの中で非同期プログラミングにおける複雑さを抑えこむのに最も有用なものだと言えるだろう。そのため、僕らのコードベースの早期のバージョンの API は Future を直接露出させたものが多かった。 ….
これが何を意味するかというと、DatasetModule インターフェイスを使っているコンシューマの視点から見ると、Future の側面のうち依存しているのは、静的に型検査された方法で複数の演算を順序付けるという能力だけだ。つまり Future の非同期に関連したさまざまな意味論ではなく、この順序付けが型によって提供される情報のうち実際に使われているものだと言える。そのため、自然と以下の一般化を行うことができる。
ここでは吉田さんと似た例を用いることにする。
import cats._, cats.data._, cats.syntax.all._
case class User(id: Long, name: String)
// In actual code, probably more than 2 errors
sealed trait Error
object Error {
final case class UserNotFound(userId: Long) extends Error
final case class ConnectionError(message: String) extends Error
}
trait UserRepos[F[_]] {
implicit def F: Monad[F]
def userRepo: UserRepo
trait UserRepo {
def followers(userId: Long): F[List[User]]
}
}
Future を使った UserRepos
UserRepos をまず Future を使って実装してみる。
import scala.concurrent.{ Future, ExecutionContext, Await }
import scala.concurrent.duration.Duration
class UserRepos0(implicit ec: ExecutionContext) extends UserRepos[Future] {
override val F = implicitly[Monad[Future]]
override val userRepo: UserRepo = new UserRepo0 {}
trait UserRepo0 extends UserRepo {
def followers(userId: Long): Future[List[User]] = Future.successful { Nil }
}
}
このようにして使う:
{
val service = new UserRepos0()(ExecutionContext.global)
service.userRepo.followers(1L)
}
// res0: Future[List[User]] = Future(Success(List()))
これで非同期な計算結果が得られた。テストのときは同期な値がほしいとする。
Id を使った UserRepos
テスト時には僕たちの計算が非同期で実行されるという事実はおそらく心配したくない。最終的に正しい結果が取得できさえすればいいからだ。 ….
ほとんどの場合は、僕たちはテストには恒等モナドを使う。例えば、先程出てきた読み込み、ソート、take、reduce を組み合わせた機能をテストしたいとする。テストフレームワークはどのモナドを使っているかを一切考えずに済む。
ここが Id データ型の出番だ。
class TestUserRepos extends UserRepos[Id] {
override val F = implicitly[Monad[Id]]
override val userRepo: UserRepo = new UserRepo0 {}
trait UserRepo0 extends UserRepo {
def followers(userId: Long): List[User] =
userId match {
case 0L => List(User(1, "Michael"))
case 1L => List(User(0, "Vito"))
case x => sys.error("not found")
}
}
}
このようにして使う:
val testRepo = new TestUserRepos {}
// testRepo: TestUserRepos = repl.MdocSession3@16945084
val ys = testRepo.userRepo.followers(1L)
// ys: Id[List[User]] = List(User(id = 0L, name = "Vito"))
抽象におけるコード
フォロワーの型コンストラクタを抽象化できたところで、10日目にも書いた相互フォローしているかどうかをチェックする isFriends を書いてみよう。
trait UserServices0[F[_]] { this: UserRepos[F] =>
def userService: UserService = new UserService
class UserService {
def isFriends(user1: Long, user2: Long): F[Boolean] =
F.flatMap(userRepo.followers(user1)) { a =>
F.map(userRepo.followers(user2)) { b =>
a.exists(_.id == user2) && b.exists(_.id == user1)
}
}
}
}
このようにして使う:
{
val testService = new TestUserRepos with UserServices0[Id] {}
testService.userService.isFriends(0L, 1L)
}
// res1: Id[Boolean] = true
これは F[] が Monad を形成するということ以外は一切何も知らずに isFriends が実装できることを示している。
F を抽象的に保ったままで中置記法の flatMap と map を使えればさらに良かったと思う。 FlatMapOps(fa) を手動で作ってみたけども、これは実行時に abstract method error になった。6日目に実装した actM マクロはうまく使えるみたいだ:
trait UserServices[F[_]] { this: UserRepos[F] =>
def userService: UserService = new UserService
class UserService {
import example.MonadSyntax._
def isFriends(user1: Long, user2: Long): F[Boolean] =
actM[F, Boolean] {
val a = userRepo.followers(user1).next
val b = userRepo.followers(user2).next
a.exists(_.id == user2) && b.exists(_.id == user1)
}
}
}
{
val testService = new TestUserRepos with UserServices[Id] {}
testService.userService.isFriends(0L, 1L)
}
// res2: Id[Boolean] = true
EitherT を用いた UserRepos
これは EitherT を使って Future にカスタムエラー型を乗せたものとも使うことができる。
class UserRepos1(implicit ec: ExecutionContext) extends UserRepos[EitherT[Future, Error, *]] {
override val F = implicitly[Monad[EitherT[Future, Error, *]]]
override val userRepo: UserRepo = new UserRepo1 {}
trait UserRepo1 extends UserRepo {
def followers(userId: Long): EitherT[Future, Error, List[User]] =
userId match {
case 0L => EitherT.right(Future { List(User(1, "Michael")) })
case 1L => EitherT.right(Future { List(User(0, "Vito")) })
case x =>
EitherT.left(Future.successful { Error.UserNotFound(x) })
}
}
}
このようにして使う:
{
import scala.concurrent.duration._
val service = {
import ExecutionContext.Implicits._
new UserRepos1 with UserServices[EitherT[Future, Error, *]] {}
}
Await.result(service.userService.isFriends(0L, 1L).value, 1 second)
}
// res3: Either[Error, Boolean] = Right(value = true)
3つのバージョンのサービスとも UserServices trait は一切変更せずに再利用できたことに注目してほしい。
今日はここまで。
14 日目
13 日目は、Id データ型、Eval データ型、「抽象的な Future」を紹介した。
SemigroupK
4日目に出てきた Semigroup は関数型プログラミングの定番で、色んな所に出てくる。
import cats._, cats.syntax.all._
List(1, 2, 3) |+| List(4, 5, 6)
// res0: List[Int] = List(1, 2, 3, 4, 5, 6)
"one" |+| "two"
// res1: String = "onetwo"
似たもので SemigroupK という型コンストラクタ F[_] のための型クラスがある。
@typeclass trait SemigroupK[F[_]] { self =>
/**
* Combine two F[A] values.
*/
@simulacrum.op("<+>", alias = true)
def combineK[A](x: F[A], y: F[A]): F[A]
/**
* Given a type A, create a concrete Semigroup[F[A]].
*/
def algebra[A]: Semigroup[F[A]] =
new Semigroup[F[A]] {
def combine(x: F[A], y: F[A]): F[A] = self.combineK(x, y)
}
}
これは combineK 演算子とシンボルを使ったエイリアスである <+> をを可能とする。使ってみる。
List(1, 2, 3) <+> List(4, 5, 6)
// res2: List[Int] = List(1, 2, 3, 4, 5, 6)
Semigroup と違って、SemigroupK は F[_] の型パラメータが何であっても動作する。
SemigroupK としての Option
Option[A] は型パラメータ A が Semigroup である時に限って Option[A] も Semigroup を形成する。そこで Semigroup を形成しないデータ型を定義して邪魔してみよう:
case class Foo(x: String)
これはうまくいかない:
Foo("x").some |+| Foo("y").some
// error: value |+| is not a member of Option[repl.MdocSession.App.Foo]
// Foo("x").some |+| Foo("y").some
// ^^^^^^^^^^^^^^^^^
だけど、これは大丈夫:
Foo("x").some <+> Foo("y").some
// res4: Option[Foo] = Some(value = Foo(x = "x"))
この 2つの型クラスの振る舞いは微妙に異なるので注意が必要だ。
1.some |+| 2.some
// res5: Option[Int] = Some(value = 3)
1.some <+> 2.some
// res6: Option[Int] = Some(value = 1)
Semigroup は Option の中身の値もつなげるが、SemigroupK の方は最初の選択する。
SemigroupK 則
trait SemigroupKLaws[F[_]] {
implicit def F: SemigroupK[F]
def semigroupKAssociative[A](a: F[A], b: F[A], c: F[A]): IsEq[F[A]] =
F.combineK(F.combineK(a, b), c) <-> F.combineK(a, F.combineK(b, c))
}
MonoidK
MonoidK もある。
@typeclass trait MonoidK[F[_]] extends SemigroupK[F] { self =>
/**
* Given a type A, create an "empty" F[A] value.
*/
def empty[A]: F[A]
/**
* Given a type A, create a concrete Monoid[F[A]].
*/
override def algebra[A]: Monoid[F[A]] =
new Monoid[F[A]] {
def empty: F[A] = self.empty
def combine(x: F[A], y: F[A]): F[A] = self.combineK(x, y)
}
....
}
これはコントラクトに empty[A] 関数を追加する。
ここでの空の値の概念は combineK に対する左右単位元として定義される。
combine と combineK の振る舞いが異なるため、Monoid[F[A]].empty と MonoidK[F].empty[A] も異なる値を取り得る。
import cats._, cats.syntax.all._
Monoid[Option[Int]].empty
// res0: Option[Int] = None
MonoidK[Option].empty[Int]
// res1: Option[Int] = None
Option[Int] に関しては、両方とも None みたいだ。
MonoidK 則
trait MonoidKLaws[F[_]] extends SemigroupKLaws[F] {
override implicit def F: MonoidK[F]
def monoidKLeftIdentity[A](a: F[A]): IsEq[F[A]] =
F.combineK(F.empty, a) <-> a
def monoidKRightIdentity[A](a: F[A]): IsEq[F[A]] =
F.combineK(a, F.empty) <-> a
}
Alternative
Alternative という Applicative と MonoidK を組み合わせた型クラスがある:
@typeclass trait Alternative[F[_]] extends Applicative[F] with MonoidK[F] { self =>
....
}
Alternative そのものは新しいメソッドや演算子を導入しない。
これは Monad 上に filter などを追加する MonadPlus を弱くした (なのでかっこいい) Applicative 版だと考えることができる。
Applicative スタイルについては3日目を参照。
Alternative 則
trait AlternativeLaws[F[_]] extends ApplicativeLaws[F] with MonoidKLaws[F] {
implicit override def F: Alternative[F]
implicit def algebra[A]: Monoid[F[A]] = F.algebra[A]
def alternativeRightAbsorption[A, B](ff: F[A => B]): IsEq[F[B]] =
(ff ap F.empty[A]) <-> F.empty[B]
def alternativeLeftDistributivity[A, B](fa: F[A], fa2: F[A], f: A => B): IsEq[F[B]] =
((fa |+| fa2) map f) <-> ((fa map f) |+| (fa2 map f))
def alternativeRightDistributivity[A, B](fa: F[A], ff: F[A => B], fg: F[A => B]): IsEq[F[B]] =
((ff |+| fg) ap fa) <-> ((ff ap fa) |+| (fg ap fa))
}
最後の法則に関しては、それが不必要では無いかという未回答なままの質問が吉田さんから出ている。
オオカミ、ヤギ、キャベツ
Justin Le (@mstk) さんが 2013年に書いた 「オオカミ、ヤギ、キャベツ: List MonadPlus とロジックパズル」 を Alternative で実装してみよう。
Wolf, Goat, Cabbage: Solving simple logic problems in #haskell using the List MonadPlus :) http://t.co/YkKi6EQdDy
— Justin Le (@mstk) December 26, 2013
ある農家の人が持ち物のオオカミ、ヤギ、キャベツを連れて川を渡ろうとしている。ところが、ボートには自分以外もう一つのものしか運ぶことができない。オオカミとヤギを放ったらかしにすると、ヤギが食べられてしまう。ヤギとキャベツを放ったらかしにすると、キャベツが食べられてしまう。損害が無いように持ち物を川の向こうまで渡らせるにはどうすればいいだろうか?
import cats._, cats.syntax.all._
sealed trait Character
case object Farmer extends Character
case object Wolf extends Character
case object Goat extends Character
case object Cabbage extends Character
case class Move(x: Character)
case class Plan(moves: List[Move])
sealed trait Position
case object West extends Position
case object East extends Position
implicit lazy val moveShow = Show.show[Move](_ match {
case Move(Farmer) => "F"
case Move(Wolf) => "W"
case Move(Goat) => "G"
case Move(Cabbage) => "C"
})
makeNMoves0
n 回の動きはこのように表現できる。
val possibleMoves = List(Farmer, Wolf, Goat, Cabbage) map {Move(_)}
// possibleMoves: List[Move] = List(
// Move(x = Farmer),
// Move(x = Wolf),
// Move(x = Goat),
// Move(x = Cabbage)
// )
def makeMove0(ps: List[List[Move]]): List[List[Move]] =
(ps , possibleMoves) mapN { (p, m) => List(m) <+> p }
def makeNMoves0(n: Int): List[List[Move]] =
n match {
case 0 => Nil
case 1 => makeMove0(List(Nil))
case n => makeMove0(makeNMoves0(n - 1))
}
テストしてみる:
makeNMoves0(1)
// res0: List[List[Move]] = List(
// List(Move(x = Farmer)),
// List(Move(x = Wolf)),
// List(Move(x = Goat)),
// List(Move(x = Cabbage))
// )
makeNMoves0(2)
// res1: List[List[Move]] = List(
// List(Move(x = Farmer), Move(x = Farmer)),
// List(Move(x = Wolf), Move(x = Farmer)),
// List(Move(x = Goat), Move(x = Farmer)),
// List(Move(x = Cabbage), Move(x = Farmer)),
// List(Move(x = Farmer), Move(x = Wolf)),
// List(Move(x = Wolf), Move(x = Wolf)),
// List(Move(x = Goat), Move(x = Wolf)),
// List(Move(x = Cabbage), Move(x = Wolf)),
// List(Move(x = Farmer), Move(x = Goat)),
// List(Move(x = Wolf), Move(x = Goat)),
// List(Move(x = Goat), Move(x = Goat)),
// List(Move(x = Cabbage), Move(x = Goat)),
// List(Move(x = Farmer), Move(x = Cabbage)),
// List(Move(x = Wolf), Move(x = Cabbage)),
// List(Move(x = Goat), Move(x = Cabbage)),
// List(Move(x = Cabbage), Move(x = Cabbage))
// )
isSolution
ヘルパー関数の
isSolution :: Plan -> Boolを定義してみよう。 基本的にh,全てのキャラクターの位置がEastであることをチェックする。
Alternative にあるものだけで filter を定義できる:
def filterA[F[_]: Alternative, A](fa: F[A])(cond: A => Boolean): F[A] =
{
var acc = Alternative[F].empty[A]
Alternative[F].map(fa) { x =>
if (cond(x)) acc = Alternative[F].combineK(acc, Alternative[F].pure(x))
else ()
}
acc
}
def positionOf(p: List[Move], c: Character): Position =
{
def positionFromCount(n: Int): Position = {
if (n % 2 == 0) West
else East
}
c match {
case Farmer => positionFromCount(p.size)
case x => positionFromCount(filterA(p)(_ == Move(c)).size)
}
}
val p = List(Move(Goat), Move(Farmer), Move(Wolf), Move(Goat))
// p: List[Move] = List(
// Move(x = Goat),
// Move(x = Farmer),
// Move(x = Wolf),
// Move(x = Goat)
// )
positionOf(p, Farmer)
// res2: Position = West
positionOf(p, Wolf)
// res3: Position = East
全ての位置が East であるかは以下のようにチェックできる:
def isSolution(p: List[Move]) =
{
val pos = (List(p), possibleMoves) mapN { (p, m) => positionOf(p, m.x) }
(filterA(pos)(_ == West)).isEmpty
}
makeMove
合法な動きとはどういうことだろう? とりあえず、農家の人が川の同じ岸にいる必要がある。
def moveLegal(p: List[Move], m: Move): Boolean =
positionOf(p, Farmer) == positionOf(p, m.x)
moveLegal(p, Move(Wolf))
// res4: Boolean = false
誰も何も食べなければ、計画は安全だと言える。つまり、オオカミとヤギ、もしくはヤギとキャベツが同じ岸にいる場合は農家の人も一緒にいる必要がある。
def safePlan(p: List[Move]): Boolean =
{
val posGoat = positionOf(p, Goat)
val posFarmer = positionOf(p, Farmer)
val safeGoat = posGoat != positionOf(p, Wolf)
val safeCabbage = positionOf(p, Cabbage) != posGoat
(posFarmer == posGoat) || (safeGoat && safeCabbage)
}
これらの関数を使って makeMove を再実装できる:
def makeMove(ps: List[List[Move]]): List[List[Move]] =
(ps, possibleMoves) mapN { (p, m) =>
if (!moveLegal(p, m)) Nil
else if (!safePlan(List(m) <+> p)) Nil
else List(m) <+> p
}
def makeNMoves(n: Int): List[List[Move]] =
n match {
case 0 => Nil
case 1 => makeMove(List(Nil))
case n => makeMove(makeNMoves(n - 1))
}
def findSolution(n: Int): Unit =
filterA(makeNMoves(n))(isSolution) map { p =>
println(p map {_.show})
}
パズルを解いてみる:
findSolution(6)
findSolution(7)
// List(G, F, C, G, W, F, G)
// List(G, F, W, G, C, F, G)
findSolution(8)
// List(G, F, C, G, W, F, G)
// List(G, F, W, G, C, F, G)
// List(G, F, C, G, W, F, G)
// List(G, F, W, G, C, F, G)
// List(G, F, C, G, W, F, G)
// List(G, F, W, G, C, F, G)
うまくいった。今日はここまで。
15日目
Cats の基礎となっている Monoid や Functor などの概念が圏論に由来することは周知のとおりだ。少し圏論を勉強してみて、その知識を Cats の理解を深めるの役立てられるか試してみよう。
圏論の初歩
僕が見た限りで最も取っ付きやすい圏論の本は Lawvere と Schanuel 共著の Conceptual Mathematics: A First Introduction to Categories 第二版だ。この本は普通の教科書のように書かれた Article という部分と Session と呼ばれる質疑や議論を含めた授業を書き取ったような解説の部分を混ぜた構成になっている。
Article の部分でも他の本と比べて基本的な概念に多くのページをさいて丁寧に解説しているので、独習者向けだと思う。
集合、射、射の合成
Conceptual Mathematics (以下 Lawvere) の和訳が無いみたいなので、僕の勝手訳になる。訳語の選択などを含め @9_ties の2013年 圏論勉強会 資料を参考にした。この場を借りてお礼します:
「圏」(category) の正確な定義を与える前に、有限集合と射という圏の一例にまず慣れ親しむべきだ。 この圏の対象 (object) は有限集合 (finite set) 別名 collection だ。 … 恐らくこのような有限集合の表記法を見たことがあるだろう:
{ John, Mary, Sam }
これは Scala だと 2通りの方法で表現できると思う。まずは a: Set[Person] という値を使った方法:
sealed trait Person {}
case object John extends Person {}
case object Mary extends Person {}
case object Sam extends Person {}
val a: Set[Person] = Set[Person](John, Mary, Sam)
// a: Set[Person] = Set(John, Mary, Sam)
もう一つの考え方は、Person という型そのものが Set を使わなくても既に有限集合となっていると考えることだ。注意: Lawvere では map という用語を使っているけども、Mac Lane や他の本に合わせて本稿では arrow を英語での用語として採用する。
この圏の射 (arrow) f は以下の3つから構成される
- 集合 A。これは射のドメイン (domain) と呼ばれる。
- 集合 B。これは射のコドメイン (codomain) と呼ばれる。
- ドメイン内のそれぞれの要素 (element, 元とも言う) a に対してコドメイン内の元 b を割り当てるルール。この b は f ∘ a (または f(a)) と表記され、「f マル a」と読む。
(射の他にも 「矢」、「写像」(map)、「函数」(function)、「変換」(transformation)、「作用素」(operator)、morphism などの言葉が使われることもある。)
好みの朝食の射を実装してみよう。
sealed trait Breakfast {}
case object Eggs extends Breakfast {}
case object Oatmeal extends Breakfast {}
case object Toast extends Breakfast {}
case object Coffee extends Breakfast {}
lazy val favoriteBreakfast: Person => Breakfast = {
case John => Eggs
case Mary => Coffee
case Sam => Coffee
}
この圏の「対象」は Set[Person] か Person であるのに対して、「射」の favoriteBreakfast は型が Person である値を受け取ることに注意してほしい。以下がこの射の内部図式 (internal diagram) だ。
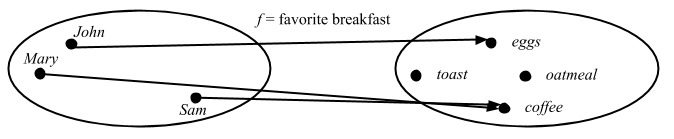
大切なのは、ドメイン内のそれぞれの黒丸から正確に一本の矢印が出ていて、その矢印がコドメイン内の何らかの黒丸に届いていることだ。
射が Function1[A, B] よりも一般的なものだということは分かるが、この圏の場合はこれで十分なので良しとする。これが favoritePerson の実装となる:
lazy val favoritePerson: Person => Person = {
case John => Mary
case Mary => John
case Sam => Mary
}
ドメインとコドメインが同一の対象の射を自己準同型射 (endomorphism) と呼ぶ。
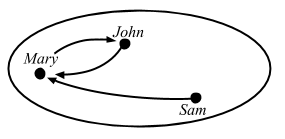
ドメインとコドメインが同一の集合 A で、かつ A 内の全ての a において f(a) = a であるものを恒等射 (identity arrow) と言う。
「A の恒等射」は 1A と表記する。
恒等射は射であるため、集合そのものというよりは集合の要素にはたらく。そのため、scala.Predef.identity を使うことができる。
identity(John)
// res0: John.type = John
上の 3つの内部図式に対応した外部図式 (external diagram) を見てみよう。

この図式を見て再び思うのは有限集合という圏においては、「対象」は Person や Breakfast のような型に対応して、射は Person => Person のような関数に対応するということだ。外部図式は Person => Person というような型レベルでのシグネチャに似ている。
圏の概念の最後の基礎部品で、圏の変化を全て担っているのが射の合成 (composition of maps) だ。これによって 2つの射を組み合わせて 3つ目の射を得ることができる。
Scala なら scala.Function1 の andThen か compose を使うことができる。
lazy val favoritePersonsBreakfast = favoriteBreakfast compose favoritePerson
これが内部図式だ:
そして外部図式:
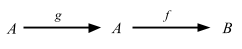
射を合成すると外部図式はこうなる:
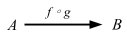
’f ∘ g’ は「f マル g」、または「f と g の合成射」と読む。
圏のデータは以下の4部品から構成される:
- 対象 (objects): A, B, C, …
- 射 (arrows): f: A => B
- 恒等射 (identity arrows): 1A: A => A
- 射の合成
これらのデータは以下の法則を満たさなければいけない:
単位元律 (The identity laws):
- If 1A: A => A, g: A => B, then g ∘ 1A = g
- If f: A => B, 1B: B => B, then 1A ∘ f = f
結合律 (The associative law):
- If f: A => B, g: B => C, h: C => D, then h ∘ (g ∘ f) = (h ∘ g) ∘ f
点
Lawvere:
単集合 (singleton) という非常に便利な集合あって、これは唯一の要素 (element; 元とも) のみを持つ。これを例えば
{me}という風に固定して、この集合を 1 と呼ぶ。
定義: ある集合の点 (point) は、1 => X という射だ。
(もし A が既に親しみのある集合なら、A から X への射を X の 「A-要素」という。そのため、「1-要素」は点となる。) 点は射であるため、他の射と合成して再び点を得ることができる。
誤解していることを恐れずに言えば、Lawvere は要素という概念を射の特殊なケースとして再定義しているように思える。単集合 (singleton) の別名に unit set というものがあって、Scala では (): Unit となる。つまり、値は Unit => X の糖衣構文だと言っているのに類似している。
lazy val johnPoint: Unit => Person = { case () => John }
lazy val johnFav = favoriteBreakfast compose johnPoint
johnFav(())
// res1: Breakfast = Eggs
関数型プログラミングをサポートする言語における第一級関数は、関数を値として扱うことで高階関数を可能とする。圏論は逆方向に統一して値を関数として扱っている。
Session 2 と 3 は Article I の復習を含むため、本を持っている人は是非読んでほしい。
Arrow
これまで見たように、射 (arrow もしくは morphism) はドメインとコドメイン間の写像だ。関数っぽい振る舞いをするものの抽象概念だと考えることもできる。
Cats では Function1[A, B]、 Kleisli[F[_], A, B]、 Cokleisli[F[_], A, B] などに対して Arrow のインスタンスが用意されている。
以下が Arrow の型クラスコントラクトだ:
package cats
package arrow
import cats.functor.Strong
import simulacrum.typeclass
@typeclass trait Arrow[F[_, _]] extends Split[F] with Strong[F] with Category[F] { self =>
/**
* Lift a function into the context of an Arrow
*/
def lift[A, B](f: A => B): F[A, B]
....
}
Category
以下は Category の型クラスコントラクトだ:
package cats
package arrow
import simulacrum.typeclass
/**
* Must obey the laws defined in cats.laws.CategoryLaws.
*/
@typeclass trait Category[F[_, _]] extends Compose[F] { self =>
def id[A]: F[A, A]
....
}
Compose
以下は Compose の型クラスコントラクトだ:
package cats
package arrow
import simulacrum.typeclass
/**
* Must obey the laws defined in cats.laws.ComposeLaws.
*/
@typeclass trait Compose[F[_, _]] { self =>
@simulacrum.op("<<<", alias = true)
def compose[A, B, C](f: F[B, C], g: F[A, B]): F[A, C]
@simulacrum.op(">>>", alias = true)
def andThen[A, B, C](f: F[A, B], g: F[B, C]): F[A, C] =
compose(g, f)
....
}
これは <<< と >>> という2つの演算子を可能とする。
import cats._, cats.data._, cats.syntax.all._
lazy val f = (_:Int) + 1
lazy val g = (_:Int) * 100
(f >>> g)(2)
// res0: Int = 300
(f <<< g)(2)
// res1: Int = 201
Strong
Haskell の Arrow tutorial を読んでみる:
first と second は既存の arrow より新たな arrow を作る。それらは、与えられた引数の1番目もしくは2番目の要素に対して変換を行う。その実際の定義は特定の arrow に依存する。
以下は Cats の Strong だ:
package cats
package functor
import simulacrum.typeclass
/**
* Must obey the laws defined in cats.laws.StrongLaws.
*/
@typeclass trait Strong[F[_, _]] extends Profunctor[F] {
/**
* Create a new `F` that takes two inputs, but only modifies the first input
*/
def first[A, B, C](fa: F[A, B]): F[(A, C), (B, C)]
/**
* Create a new `F` that takes two inputs, but only modifies the second input
*/
def second[A, B, C](fa: F[A, B]): F[(C, A), (C, B)]
}
これは first[C] と second[C] というメソッドを可能とする。
lazy val f_first = f.first[Int]
f_first((1, 1))
// res2: (Int, Int) = (2, 1)
lazy val f_second = f.second[Int]
f_second((1, 1))
// res3: (Int, Int) = (1, 2)
ここで f は 1を加算する関数であるため、f_first と f_second が何をやっているかは明らかだと思う。
Split
(***)は 2つの射を値のペアに対して (1つの射はペアの最初の項で、もう 1つの射はペアの 2つめの項で) 実行することで 1つの新しいに射へと組み合わせる。
Cats ではこれは split と呼ばれる。
package cats
package arrow
import simulacrum.typeclass
@typeclass trait Split[F[_, _]] extends Compose[F] { self =>
/**
* Create a new `F` that splits its input between `f` and `g`
* and combines the output of each.
*/
def split[A, B, C, D](f: F[A, B], g: F[C, D]): F[(A, C), (B, D)]
}
これは split 演算子として使うことができる:
(f split g)((1, 1))
// res4: (Int, Int) = (2, 100)
同型射
Lawvere:
定義: ある射 f: A => B に対して g ∘ f = 1A と f ∘ g = 1B の両方を満たす射 g: B => A が存在するとき、f を同型射 (isomorphism) または可逆な射 (invertible arrow) であるという。 また、1つでも同型射 f: A => B が存在するとき、2つの対象 A と B は同型 (isomorphic) であるという。
残念ながら Cats には同型射を表すデータ型が無いため、自前で定義する必要がある。
import cats._, cats.data._, cats.syntax.all._, cats.arrow.Arrow
object Isomorphisms {
trait Isomorphism[Arrow[_, _], A, B] { self =>
def to: Arrow[A, B]
def from: Arrow[B, A]
}
type IsoSet[A, B] = Isomorphism[Function1, A, B]
type <=>[A, B] = IsoSet[A, B]
}
import Isomorphisms._
Family から Relic への同型射は以下のように定義できる。
sealed trait Family {}
case object Mother extends Family {}
case object Father extends Family {}
case object Child extends Family {}
sealed trait Relic {}
case object Feather extends Relic {}
case object Stone extends Relic {}
case object Flower extends Relic {}
lazy val isoFamilyRelic = new (Family <=> Relic) {
val to: Family => Relic = {
case Mother => Feather
case Father => Stone
case Child => Flower
}
val from: Relic => Family = {
case Feather => Mother
case Stone => Father
case Flower => Child
}
}
射の等価性
これをテストするためには、まず2つの関数を比較するテストを実装することができる。2つの射は 3つの材料が同一である場合に等価であると言える。
- ドメイン A
- コドメイン B
- f ∘ a を割り当てるルール
ScalaCheck だとこう書ける:
scala> import org.scalacheck.{Prop, Arbitrary, Gen}
import org.scalacheck.{Prop, Arbitrary, Gen}
scala> import cats._, cats.data._, cats.implicits._
import cats._
import cats.data._
import cats.implicits._
scala> def func1EqualsProp[A, B](f: A => B, g: A => B)
(implicit ev1: Eq[B], ev2: Arbitrary[A]): Prop =
Prop.forAll { a: A =>
f(a) === g(a)
}
func1EqualsProp: [A, B](f: A => B, g: A => B)(implicit ev1: cats.Eq[B], implicit ev2: org.scalacheck.Arbitrary[A])org.scalacheck.Prop
scala> val p1 = func1EqualsProp((_: Int) + 2, 1 + (_: Int))
p1: org.scalacheck.Prop = Prop
scala> p1.check
! Falsified after 0 passed tests.
> ARG_0: 0
scala> val p2 = func1EqualsProp((_: Int) + 2, 2 + (_: Int))
p2: org.scalacheck.Prop = Prop
scala> p2.check
+ OK, passed 100 tests.
同型射のテスト
scala> :paste
implicit val familyEqual = Eq.fromUniversalEquals[Family]
implicit val relicEqual = Eq.fromUniversalEquals[Relic]
implicit val arbFamily: Arbitrary[Family] = Arbitrary {
Gen.oneOf(Mother, Father, Child)
}
implicit val arbRelic: Arbitrary[Relic] = Arbitrary {
Gen.oneOf(Feather, Stone, Flower)
}
// Exiting paste mode, now interpreting.
familyEqual: cats.kernel.Eq[Family] = cats.kernel.Eq$$anon$116@99f2e3d
relicEqual: cats.kernel.Eq[Relic] = cats.kernel.Eq$$anon$116@159bd786
arbFamily: org.scalacheck.Arbitrary[Family] = org.scalacheck.ArbitraryLowPriority$$anon$1@799b3915
arbRelic: org.scalacheck.Arbitrary[Relic] = org.scalacheck.ArbitraryLowPriority$$anon$1@36c230c0
scala> func1EqualsProp(isoFamilyRelic.from compose isoFamilyRelic.to, identity[Family] _).check
+ OK, passed 100 tests.
scala> func1EqualsProp(isoFamilyRelic.to compose isoFamilyRelic.from, identity[Relic] _).check
+ OK, passed 100 tests.
テストはうまくいったみたいだ。今日はここまで。
16日目
15日目は Lawvere と Schanuel の『Conceptual Mathematics: A First Introduction to Categories』を使って圏論の基本となる概念をみてきた。この本は、基本的な概念の説明に具体例を使って多くのページを割いているので「圏」という概念の入門には向いてると思う。ただ、より高度な概念に進もうとしたときには、周りくどく感じてしまう。
Awodey の『Category Theory』
今日からは Steve Awodey氏の Category Theory に変えることにする。これは @9_ties さんの 2013年 圏論勉強会でも使われたものだ。この本も数学者じゃない人向けに書かれているけども、もう少し速いペースで進むし、抽象的思考に重点を置いている。
定義や定理が圏論的な概念のみに基づいていて、対象や射に関する追加の情報によらないとき、それらは抽象的 (abstract) であるという。抽象的な概念の利点は、即座にそれが全ての圏に適用できることだ。
定義 1.3 任意の圏 C において、ある射 f: A => B に対して以下の条件を満たす g: B => A が C 内にあるとき、その射は同型射 (isomorphism) であるという:
g ∘ f = 1A かつ f ∘ g = 1B。
この定義は圏論的な概念しか用いないため、Awodey は抽象的概念の一例として挙げている。
Milewski の 『Category Theory for Programmers』
もう一つ副読本としてお勧めしたいのは Bartosz Milewski (@bartoszmilewski) さんがオンラインで執筆中の Category Theory for Programmers という本だ。
Sets
抽象的に行く前に具象圏をいくつか紹介する。昨日は一つの圏の話しかしてこなかったので、これは役に立つことだと思う。
集合と全域関数 (total function) の圏は太字で Sets と表記する。
Scala では、大雑把に言うとこれは Int => String というように型と関数によってエンコードできる。
だけど、プログラミング言語はボトム型 (Nothing)、例外、停止しない (non-terminating) コードなどを許容するので、このエンコーディングが正しいのかという哲学的な議論があるらしい。便宜上、本稿ではこの問題を無視して Sets をエンコードできるふりをする。
Setsfin
全ての有限集合とその間の全域関数を Setsfin という。今まで見てきた圏がこれだ。
Pos
Awodey は和訳が見つからなかったので勝手訳になる:
数学でよく見るものに構造的集合 (structured set)、つまり集合に何らかの「構造」を追加したものと、それを「保存する」関数の圏というものがある。(構造と保存の定義は独自に与えられる)
半順序集合 (partially ordered set)、または略して poset と呼ばれる集合 A は、全ての a, b, c ∈ A に対して以下の条件が成り立つ二項関係 a ≤A b を持つ:
- 反射律 (reflexivity): a ≤A a
- 推移律 (transitivity): もし a ≤A b かつ b ≤A c ならば a ≤A c
- 反対称律 (antisymmetry): もし a ≤A b かつ b ≤A a ならば a = b
poset A から poset B への射は単調 (monotone) な関数 m: A => B で、これは全ての a, a’ ∈ A に対して以下が成り立つという意味だ:
- a ≤A a’ のとき m(a) ≤A m(a’)
関数が単調 (monotone) であるかぎり対象は圏の中にとどまるため、「構造」が保存されると言える。poset と単調関数の圏は Pos と表記される。Awodey は poset が好きなので、これを理解しておくのは重要。
poset の例としては Int 型があり、≤ として PartialOrder 型クラスで定義されているように整数の比較である <= を使う。
別の例として、case class LString(value: String) を考えてみる。≤ としては value の文字列の長さを比較に使う。
scala> :paste
// Entering paste mode (ctrl-D to finish)
case class LString(value: String)
val f: Int => LString = (x: Int) => LString(if (x < 0) "" else x.toString)
// Exiting paste mode, now interpreting.
defined class LString
f: Int => LString = <function1>
scala> f(0)
res0: LString = LString(0)
scala> f(10)
res1: LString = LString(10)
上の f は、f(0) ≤ f(10) および a <= a' を満たす任意の Int において f(a) ≤ f(a') であるため、単調である。
有限圏
Awodey:
もちろん、圏の対象は集合である必要は無い。以下は非常に簡単な例だ:
- 圏 1 は以下のようにみえる:
これは、1つの対象とその (図では省かれている) 恒等射を持つ。- 圏 2 は以下のようにみえる:
これは、2つの対象、それらの恒等射、そして対象の間にただ 1つの射を持つ。- 圏 3 は以下のようにみえる:
これは、3つの対象、それらの恒等射、第1の対象から第2の対象へのただ 1つの射、第2の対象から第2の対象へのただ 1つの射、そして第1の対象から第3の対象へのただ 1つの射 (前の 2つの射の合成) を持つ。- 圏 0 は以下のようにみえる:
これは、一切の対象や射を持たない。
これらの圏は直接はあんまり使い道が無いけども、圏とは何かという考えるにあたって頭を柔らかくするのと、他の概念へのつなぎとして訳に立つと思う。
Cat
Awodey:
定義 1.2. 函手 (functor)
F: C => D
は、圏 C と圏 D の間で以下の条件が成り立つように対象を対象に、また射を射に転写する:
- F(f: A => B) = F(f): F(A) => F(B)
- F(1A) = 1F(A)
- F(g ∘ f) = F(g) ∘ F(f)
つまり、F はドメインとコドメイン、恒等射、および射の合成を保存する。
ついにきた。函手 (functor) は 2つの圏の間の射だ。以下が外部図式となる:
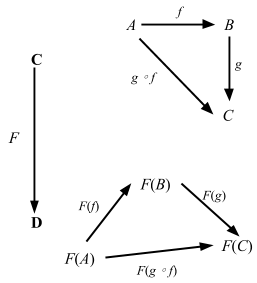
F(A)、 F(B)、 F(C) の位置が歪んでいるのは意図的なものだ。F は上の図を少し歪ませているけども、射の合成関係は保存している。
この圏と函手の圏は Cat と表記される。
ここで表記規則をおさらいしておこう。
大文字、斜体の A、B、C は対象を表す (Sets において、これらは Int や String に対応する)。
一方、大文字、太字の C と D は圏を表す。圏は、これまでに見てきた List[A] を含み色んな種類のものでありうる。つまり、函手 F: C => D はただの関数ではなく、2つの圏の間の射だということに注意してほしい。
そういう意味では、プログラマが「Functor」と言った場合は、C 側が Sets に決め打ちされた非常に限定された種類の函手を指しているといえる。
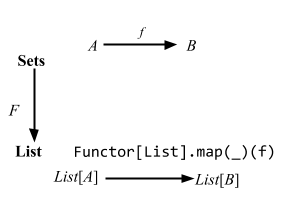
圏としてのモノイド
Awodey:
モノイド (単位元を持つ半群とも呼ばれる) は、集合 M で、二項演算 ·: M × M => M と特定の「単位元」(unit) u ∈ M を持ち、任意の x, y, z ∈ M に対して以下の条件を満たすもの:
- x · (y · z) = (x · y) · z
- u · x = x = x · u
同義として、モノイドは唯一つの対象を持つ圏である。その圏の射はモノイドの要素だ。特に恒等射は単位元 u である。射の合成はモノイドの二項演算 m · n だ。
モノイドが Cats でどうエンコードされるかは 4日目の Monoid) をみてほしい。
trait Monoid[@sp(Int, Long, Float, Double) A] extends Any with Semigroup[A] {
def empty: A
....
}
trait Semigroup[@sp(Int, Long, Float, Double) A] extends Any with Serializable {
def combine(x: A, y: A): A
....
}
Int と 0 の加算は以下のように書ける:
scala> 10 |+| Monoid[Int].empty
res26: Int = 10
このモノイドがただ一つの対象を持つ圏という考え方は「何を言っているんだ」と前は思ったものだけど、単集合を見ているので今なら理解できる気がする。
ここで注意してほしいのは、上の (Int, +) モノイドにおいては、射は文字通り 0、1、2 などであって関数ではないということだ。
Mon
モノイドに関連する圏がもう一つある。 モノイドとモノイドの構造を保存した関数の圏は Mon と表記される。このような構造を保存する射は準同型写像 (homomorphism) と呼ばれる。
モノイド M からモノイド N への準同型写像は、関数 h: M => N で全ての m, n ∈ M について以下の条件を満たすも
- h(m ·M n) = h(m) ·N h(n)
- h(uM) = uN
それぞれのモノイドは圏なので、モノイド準同型写像 (monoid homomorphism) は函手 (functor) の特殊形だと言える。
Grp
Awodey:
定義 1.4 群 (group) G は、モノイドのうち全ての要素 g に対して逆射 (inverse) g-1 を持つもの。つまり、G は唯一つの対象を持つ圏で、全ての射が同型射となっている。
cats.kernel.Monoid の型クラスコントラクトはこうなっている:
/**
* A group is a monoid where each element has an inverse.
*/
trait Group[@sp(Int, Long, Float, Double) A] extends Any with Monoid[A] {
/**
* Find the inverse of `a`.
*
* `combine(a, inverse(a))` = `combine(inverse(a), a)` = `empty`.
*/
def inverse(a: A): A
}
syntax がインポートされていてば、これは inverse メソッドを可能とする:
import cats._, cats.syntax.all._
1.inverse
// res0: Int = -1
assert((1 |+| 1.inverse) === Monoid[Int].empty)
群 (group) と群の準同型写像 (group homomorphism、群の構造を保存する関数) の圏は Grp と表記される。
忘却函手
準同型写像という用語が何回か出てきたが、構造を保存しない関数を考えることもできる。 全ての群 G はモノイドでもあるので、f: G => M という G から逆射の能力を失わせて中のモノイドだけを返す関数を考えることができる。さらに、群とモノイドは両方とも圏であるので、f は函手であると言える。
これを Grp 全体に広げて、F: Grp => Mon という函手を考えることができる。このような構造を失わせるような函手を忘却函手 (forgetful functor) という。Scala でこれを考えると、A: Group から始めて、何らかの方法で戻り値を A: Monoid にダウングレードさせる感じだろうか。
今日はここまで。
17 日目
16日目は、Awodey氏の「Category Theory」をたよりにいくつかの具象圏をみてみた。
これで抽象構造について話すことができる。定義や定理が圏論的な概念のみに基づいていて、対象や射に関する追加の情報によらないとき、それらは抽象的 (abstract) であるという。同型射の定義はその一例だ:
定義 1.3 任意の圏 C において、ある射 f: A => B に対して以下の条件を満たす g: B => A が C 内にあるとき、その射は同型射 (isomorphism) であるという:
g ∘ f = 1A かつ f ∘ g = 1B。
今後この同型射も道具箱に取り込んで、他の概念を探索する。
始対象と終対象
ある定義が圏論的な概念 (対象と射) のみに依存すると、よく「図式 abc が与えられたとき、別の図式 xyz が可換となる (commute) ような唯一の x が存在する」という形式になる。この場合の可換性とは、全ての射が正しく合成できるといった意味だ。このような定義は普遍性 (universal property) または普遍写像性 (universal mapping property) と呼ばれ、英語だと長いので UMP と略される。
集合論から来る概念もあるけども、抽象的な性質からより強力なものになっている。Sets の空集合と唯一つだけの要素を持つ集合を抽象化することを考えてみる。
定義 2.9 任意の圏 C において、
- 始対象 (initial) 0 は、任意の対象 C に対して以下を満たす一意の射を持つ

- 終対象 (terminal) 1 は、任意の対象 C に対して以下を満たす一意の射を持つ

この2つの図式はシンプルに見えすぎて逆に分かりづらいが、UMP の形になっていることに注意してほしい。最初のものは、この図式が与えられ 0 が存在するとき、0 => C は一意であると言っている。
同型を除いて一意
普遍写像性一般に言えることとして、一意と言った場合にこの要件は同型を除く (unique up to isomorphism) ということだ。考え方を変えると、もし対象 A と B が同型ならば「何らかの意味で等しい」ということでもある。これを記号化して A ≅ B と表記する。
命題 2.10 全ての始対象 (終対象) は同型を除いて一意である
証明。もし仮に C と C’ が両方とも同じ圏内の任意の始対象 (終対象) であるならば、そこには一意の同型射 C => C’ が存在する。0 と 0’ がある圏 C の始対象であるとする。以下の図式により、0 と 0’ が一意に同型であることは明らか:
同型射の定義は g ∘ f = 1A かつ f ∘ g = 1B なので、確かにこれで合ってる。
始対象の例
抽象構造の面白いのは、別の圏において一見異なる形で表れることだ。
Sets 圏において、空集合は始対象であり、任意の単集合 {x} は終対象だ。
Sets は型とその間の関数によってエンコードできることを思い出してほしい。Scala で空の型と言えば Nothing ということになるかもしれない。つまり、Nothing から A に対して、ただ1つの関数しか得られないということだ。Milewski氏によると、Haskell には absurd という関数がある。実装してみるとこういうふうになるかもしれない:
def absurd[A]: Nothing => A = { case _ => ??? }
absurd[Int]
// res0: Function1[Nothing, Int] = <function1>
この関数のドメインには値が無いので、本文は絶対に実行されないはずだ。
poset では、対象は最小の要素を持つとき始対象で、最大の要素を持つ場合に終対象となる。
poset では ≤ の構造を保存しなければいけないので、何となく分かる気がする。
終対象の例
単集合は、型に 1つの値しかないことを意味する。Scala だと、Unit がその一例となる。一般的な A から Unit に対する関数は唯一の実装となる:
def unit[A](a: A): Unit = ()
unit(1)
これにより Unit は、Sets圏における終対象となるが、Scala では object と書くだけでいくらでもシングルトン型を定義できる:
case object Single
def single[A](a: A): Single.type = Single
single("test")
// res2: Single.type = Single
上に書いてあるとおり、poset では最大の要素を持つ場合に終対象となる。
積
まずは集合の積を考える。集合 A と B があるとき、A と B のデカルト積は順序対 (ordered pairs) の集合となる
A × B = {(a, b)| a ∈ A, b ∈ B}
2つの座標射影 (coordinate projection) があって:
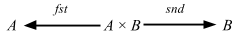
これは以下の条件を満たす:
- fst ∘ (a, b) = a
- snd ∘ (a, b) = b
この積という考えは case class やタプルの基底 trait である scala.Product にも関連する。
任意の要素 c ∈ A × B に対して、c = (fst ∘ c, snd ∘ c) ということができる。
15日目に出てきたが、明示的に単集合 1 を導入することで要素という概念を一般化できる。
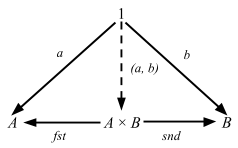
これをすこしきれいに直すと、積の圏論的な定義を得ることができる:
定義 2.15. 任意の圏 C において、対象 A と B の積の図式は対象 P と射 p1 と p2 から構成され
以下の UMP を満たす:この形となる任意の図式があるとき
次の図式
が可換となる (つまり、x1 = p1 u かつ x2 = p2 u が成立する) 一意の射 u: X => P が存在する。
「一意の射」と出てきたら UMP だなと見当がつく。
積の一意性
Sets に立ち返ると、型A と型B があるとき、(A, B) を返す一意の関数があると言っているだけだ。しかし、これが全ての圏に当てはまるかどう証明すればいいだろう? 使って良いのはアルファベットと矢印だけだ。
命題 2.17 積は同型を除いて一意である。
P と Q が対象 A と B の積であるとする。
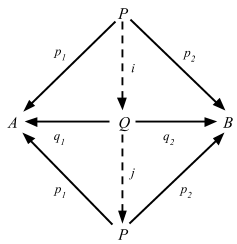
- P は積であるため、p1 = q1 ∘ i かつ p2 = q2 ∘ i を満たす一意の i: P => Q が存在する。
- Q は積であるため、q1 = p1 ∘ j かつ q2 = p2 ∘ j を満たす一意の j: Q => P が存在する。
- i と j を合成することで 1P = j ∘ i が得られる。
- 同様にして 1Q = i ∘ j。
- i は同型射、P ≅ Q である。∎
全ての積は同型であるため、一つを取って A × B と表記する。また、射 u: X => A × B は ⟨x1, x2⟩ と表記する。
双対性
逆圏
双対性に入る前に、既存の圏から別の圏を生成するということを話しておく必要がある。ここで注意してほしいのは、今まで取り扱ってきた対象ではなくて圏の話をしているということで、これは対象と射の両方を含む。
任意の圏 C の逆圏 (opposite category、また dual「双対圏」とも) Cop は、C と同じ対象を持つが、Cop 内の射は C では f: D => C である。つまり、Cop は C の射を形式的に逆向きにしたものだ。
双対性原理
この考えをさらに進めて、圏論内の任意の文 Σ の以下を置換して「双対文」Σ* を得ることができる。
- f ∘ g の代わりに g ∘ f
- コドメインの代わりにドメイン
- ドメインの代わりにコドメイン
意味論的にどれが f で g なのかに重要性は無いため、Σ が圏論のみに基づいているかぎり双対文も成り立つ。そのため、ある概念についての任意の証明はその双対に対しても成り立つ。これは双対性原理 (duality principle) と呼ばれる。
別の見方をすると、もし Σ が全ての圏 C について成り立つとした場合、Cop でも成り立つことになる。そのため、Σ* は (Cop)op、つまり C でも成り立つことになる。
始対象と終対象の定義をもう一度見てみよう:
定義 2.9 任意の圏 C において、
- 始対象 (initial) 0 は、任意の対象 C に対して以下を満たす一意の射を持つ
0 => C- 終対象 (terminal) 1 は、任意の対象 C に対して以下を満たす一意の射を持つ
C => 1
これはお互いの双対となっているため、圏 C での始対象は逆圏 Cop での終対象となる。
ここで「全ての始対象は同型を除いて一意である」という命題の定義を思い出してほしい。

上の図式内の全ての射の方向を逆転すると、終対象に関する証明が得られる。
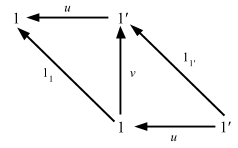
これは結構すごい。
余積
双対としてよく知られているものに、積の双対である余積 (coproduct、「直和」とも) がある。双対を表すのに英語では頭に “co-” を、日本語だと「余」を付ける。
以下に積の定義を再掲する:
定義 2.15. 任意の圏 C において、対象 A と B の積の図式は対象 P と射 p1 と p2 から構成され
以下の UMP を満たす:この形となる任意の図式があるとき
次の図式
が可換となる (つまり、x1 = p1 u かつ x2 = p2 u が成立する) 一意の射 u: X => P が存在する。
矢印をひっくり返すと余積図式が得られる:
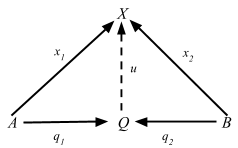
余積は同型を除いて一意なので、余積は A + B、u: A + B => X の射は [f, g] と表記することができる。
「余射影」の i1: A => A + B と i2: B => A + B は、単射 (“injective”) ではなくても「単射」 (“injection”) という。
「埋め込み」(embedding) ともいうみたいだ。積が scala.Product などでエンコードされる直積型に関係したように、余積は直和型 (sum type, disjoint union type) と関連する。
代数的データ型
A + B をエンコードする最初の方法は sealed trait と case class を使う方法だ。
sealed trait XList[A]
object XList {
case class XNil[A]() extends XList[A]
case class XCons[A](head: A, rest: XList[A]) extends XList[A]
}
XList.XCons(1, XList.XNil[Int])
// res0: XList.XCons[Int] = XCons(head = 1, rest = XNil())
余積としての Either データ型
目をすくめて見ると Either を直和型だと考えることもできる。Either の型エイリアスとして |: を定義する:
type |:[+A1, +A2] = Either[A1, A2]
Scala は型コンストラクタに中置記法を使えるので、Either[String, Int] の代わりに String |: Int と書けるようになった。
val x: String |: Int = Right(1)
// x: String |: Int = Right(value = 1)
ここまでは普通の Scala 機能しか使っていない。Cats は単射 i1: A => A + B と i2: B => A + B を表す cats.Injection という型クラスを提供する。これを使うと Left と Right を気にせずに coproduct を作ることができる。
import cats._, cats.data._, cats.syntax.all._
val a = Inject[String, String |: Int].inj("a")
// a: String |: Int = Left(value = "a")
val one = Inject[Int, String |: Int].inj(1)
// one: String |: Int = Right(value = 1)
値を再取得するには prj を呼ぶ:
Inject[String, String |: Int].prj(a)
// res1: Option[String] = Some(value = "a")
Inject[String, String |: Int].prj(one)
// res2: Option[String] = None
apply と unapply を使って書くときれいに見える:
lazy val StringInj = Inject[String, String |: Int]
lazy val IntInj = Inject[Int, String |: Int]
val b = StringInj("b")
// b: String |: Int = Left(value = "b")
val two = IntInj(2)
// two: String |: Int = Right(value = 2)
two match {
case StringInj(x) => x
case IntInj(x) => x.show + "!"
}
// res3: String = "2!"
|: にコロンを入れた理由は右結合にするためで、3つ以上の型を使うときに便利だからだ:
val three = Inject[Int, String |: Int |: Boolean].inj(3)
// three: String |: Int |: Boolean = Right(value = Left(value = 3))
見ての通り、戻り値の型は String |: (Int |: Boolean) となった。
Curry-Howard エンコーディング
関連して Miles Sabin (@milessabin) さんの Unboxed union types in Scala via the Curry-Howard isomorphism も興味深い。
Shapeless.Coproduct
Shapeless の Coproducts and discriminated unions も参考になる。
EitherK データ型
Cats には EitherK[F[_], G[_], A] というデータ型があって、これは型コンストラクタにおける Either だ。
Data types à la carte で、Wouter Swierstra (@wouterswierstra) さんがこれを使っていわゆる Expression Problem と呼ばれているものを解決できると解説している。
今日はここまで。
18日目
17日目は、Awodey氏の「Category Theory」をたよりに始対象と終対象、積、双対性といった抽象構造をみた。

エフェクトシステム
Lazy Functional State Threads において John Launchbury さんと Simon Peyton-Jones さん曰く::
Based on earlier work on monads, we present a way of securely encapsulating stateful computations that manipulate multiple, named, mutable objects, in the context of a non-strict purely-functional language.
Scala には var があるので、可変性をカプセル化するのは一見すると無意味に思えるかもしれないが、stateful な計算を抽象化すると役に立つこともある。並列に実行される計算など特殊な状況下では、状態が共有されないかもしくは慎重に共有されているかどうかが正誤を分ける
Cats のエコシステムでは Cats Effect と Monix の両者がエフェクトシステムを提供する。State Threads を流しつつ Cats Effect をみていこう。
Cats Effect sbt セットアップ
val catsEffectVersion = "3.0.2"
val http4sVersion = "1.0.0-M21"
val catsEffect = "org.typelevel" %% "cats-effect" % catsEffectVersion
val http4sBlazeClient = "org.http4s" %% "http4s-blaze-client" % http4sVersion
val http4sCirce = "org.http4s" %% "http4s-circe" % http4sVersion
Ref
LFST:
What is a “state”? Part of every state is a finite mapping from reference to values. … A reference can be thought of as the name of (or address of) a variable, an updatable location in the state capable of holding a value.
Ref は Cats Effect の IO モナドのコンテキストの内部で使われる、スレッドセーフな可変変数だ。
Ref 曰く:
Ref は、そのコンテンツの安全な並列アクセスと変更を提供するが、同期機能は持たない。
trait RefSource[F[_], A] {
/**
* Obtains the current value.
*
* Since `Ref` is always guaranteed to have a value, the returned action
* completes immediately after being bound.
*/
def get: F[A]
}
trait RefSink[F[_], A] {
/**
* Sets the current value to `a`.
*
* The returned action completes after the reference has been successfully set.
*
* Satisfies:
* `r.set(fa) *> r.get == fa`
*/
def set(a: A): F[Unit]
}
abstract class Ref[F[_], A] extends RefSource[F, A] with RefSink[F, A] {
/**
* Modifies the current value using the supplied update function. If another modification
* occurs between the time the current value is read and subsequently updated, the modification
* is retried using the new value. Hence, `f` may be invoked multiple times.
*
* Satisfies:
* `r.update(_ => a) == r.set(a)`
*/
def update(f: A => A): F[Unit]
def modify[B](f: A => (A, B)): F[B]
....
}
このように使うことができる:
import cats._, cats.syntax.all._
import cats.effect.{ IO, Ref }
def e1: IO[Ref[IO, Int]] = for {
r <- Ref[IO].of(0)
_ <- r.update(_ + 1)
} yield r
def e2: IO[Int] = for {
r <- e1
x <- r.get
} yield x
{
import cats.effect.unsafe.implicits._
e2.unsafeRunSync()
}
// res0: Int = 1
e1 は 0 で初期化した新しい Ref を作成して、1 を加算して変更する。e2 は e1 と合成して、内部値を取得する。最後に、エフェクトを実行するために unsafeRunSync() を呼ぶ。
IO データ型
Launchbury と SPJ が State Thread を用いたように、Cats Effect はライトウェイトなスレッド的概念であるファイバーと呼ばれるものを使ってエフェクトをモデル化する。
sealed abstract class IO[+A] private () extends IOPlatform[A] {
def flatMap[B](f: A => IO[B]): IO[B] = IO.FlatMap(this, f)
....
// from IOPlatform
final def unsafeRunSync()(implicit runtime: unsafe.IORuntime): A
}
object IO extends IOCompanionPlatform with IOLowPriorityImplicits {
/**
* Suspends a synchronous side effect in `IO`.
*
* Alias for `IO.delay(body)`.
*/
def apply[A](thunk: => A): IO[A] = Delay(() => thunk)
def delay[A](thunk: => A): IO[A] = apply(thunk)
def async[A](k: (Either[Throwable, A] => Unit) => IO[Option[IO[Unit]]]): IO[A] =
asyncForIO.async(k)
def async_[A](k: (Either[Throwable, A] => Unit) => Unit): IO[A] =
asyncForIO.async_(k)
def canceled: IO[Unit] = Canceled
def cede: IO[Unit] = Cede
def sleep(delay: FiniteDuration): IO[Unit] =
Sleep(delay)
def race[A, B](left: IO[A], right: IO[B]): IO[Either[A, B]] =
asyncForIO.race(left, right)
def readLine: IO[String] =
Console[IO].readLine
def print[A](a: A)(implicit S: Show[A] = Show.fromToString[A]): IO[Unit] =
Console[IO].print(a)
def println[A](a: A)(implicit S: Show[A] = Show.fromToString[A]): IO[Unit] =
Console[IO].println(a)
def blocking[A](thunk: => A): IO[A] =
Blocking(TypeBlocking, () => thunk)
def interruptible[A](many: Boolean)(thunk: => A): IO[A] =
Blocking(if (many) TypeInterruptibleMany else TypeInterruptibleOnce, () => thunk)
def suspend[A](hint: Sync.Type)(thunk: => A): IO[A] =
if (hint eq TypeDelay)
apply(thunk)
else
Blocking(hint, () => thunk)
....
}
Hello world
以下は Cats Effect IO を用いた hello world のプログラムだ。
package example
import cats._, cats.syntax.all._
import cats.effect.IO
object Hello extends App {
val program = for {
_ <- IO.print("What's your name? ")
x <- IO.readLine
_ <- IO.println(s"Hello, $x")
} yield ()
}
実行するとこのようになる:
> run
[info] running example.Hello
[success] Total time: 1 s, completed Apr 11, 2021 12:51:44 PM
何も起こらなかったはずだ。標準ライブラリの scala.concurrent.Future + 普通の ExecutionContext と違って、IO データ型は停止状態のエフェクトを表し、明示的に実行するまで実行されない。
以下のように走らせることができる:
package example
import cats._, cats.syntax.all._
import cats.effect.IO
object Hello extends App {
val program = for {
_ <- IO.print("What's your name? ")
x <- IO.readLine
_ <- IO.println(s"Hello, $x")
} yield ()
import cats.effect.unsafe.implicits.global
program.unsafeRunSync()
}
これで副作用が見えるようになった:
sbt:herding-cats> run
[info] running example.Hello
What's your name? eugene
Hello, eugene
[success] Total time: 4 s, completed Apr 11, 2021 1:00:19 PM
実際のプログラムを書くときは IOApp というより良いプログラムハーネスがあるので、それを使う:
import cats._, cats.syntax.all._
import cats.effect.{ ExitCode, IO, IOApp }
object Hello extends IOApp {
override def run(args: List[String]): IO[ExitCode] =
program.as(ExitCode.Success)
lazy val program = for {
_ <- IO.print("What's your name? ")
x <- IO.readLine
_ <- IO.println(s"Hello, $x")
} yield ()
}
これらの例は IO データ型がモナディックに合成可能であることを例示するが、実行は逐次的だ。
Pizza app
もう少し IO の何が嬉しいのかを示すために、http4s client を使ったピザアプリを考える。
import cats._, cats.syntax.all._
import cats.effect.IO
import org.http4s.client.Client
def withHttpClient[A](f: Client[IO] => IO[A]): IO[A] = {
import java.util.concurrent.Executors
import scala.concurrent.ExecutionContext
import org.http4s.client.blaze.BlazeClientBuilder
val threadPool = Executors.newFixedThreadPool(5)
val httpEc = ExecutionContext.fromExecutor(threadPool)
BlazeClientBuilder[IO](httpEc).resource.use(f)
}
def search(httpClient: Client[IO], q: String): IO[String] = {
import io.circe.Json
import org.http4s.Uri
import org.http4s.circe._
val baseUri = Uri.unsafeFromString("https://api.duckduckgo.com/")
val target = baseUri
.withQueryParam("q", q + " pizza")
.withQueryParam("format", "json")
httpClient.expect[Json](target) map { json =>
json.findAllByKey("Abstract").headOption.flatMap(_.asString).getOrElse("")
}
}
{
import cats.effect.unsafe.implicits.global
val program = withHttpClient { httpClient =>
search(httpClient, "New York")
}
program.unsafeRunSync()
}
// res0: String = "New York\u2013style pizza is pizza made with a characteristically large hand-tossed thin crust, often sold in wide slices to go. The crust is thick and crisp only along its edge, yet soft, thin, and pliable enough beneath its toppings to be folded in half to eat. Traditional toppings are simply tomato sauce and shredded mozzarella cheese. This style evolved in the U.S. from the pizza that originated in New York City in the early 1900s, itself derived from the Neapolitan-style pizza made in Italy. Today it is the dominant style eaten in the New York Metropolitan Area states of New York, and New Jersey and variously popular throughout the United States. Regional variations exist throughout the Northeast and elsewhere in the U.S."
これは Duck Duck Go API に New York スタイルのピザのクエリをする。ネットワーク IO によるレイテンシーを低下させるために、並列呼び出しをしたい:
{
import cats.effect.unsafe.implicits.global
val program = withHttpClient { httpClient =>
val xs = List("New York", "Neapolitan", "Sicilian", "Chicago", "Detroit", "London")
xs.parTraverse(search(httpClient, _))
}
program.unsafeRunSync()
}
// res1: List[String] = List(
// "New York\u2013style pizza is pizza made with a characteristically large hand-tossed thin crust, often sold in wide slices to go. The crust is thick and crisp only along its edge, yet soft, thin, and pliable enough beneath its toppings to be folded in half to eat. Traditional toppings are simply tomato sauce and shredded mozzarella cheese. This style evolved in the U.S. from the pizza that originated in New York City in the early 1900s, itself derived from the Neapolitan-style pizza made in Italy. Today it is the dominant style eaten in the New York Metropolitan Area states of New York, and New Jersey and variously popular throughout the United States. Regional variations exist throughout the Northeast and elsewhere in the U.S.",
// "Neapolitan pizza also known as Naples-style pizza, is a style of pizza made with tomatoes and mozzarella cheese. It must be made with either San Marzano tomatoes or Pomodorino del Piennolo del Vesuvio, which grow on the volcanic plains to the south of Mount Vesuvius, and Mozzarella di Bufala Campana, a protected designation of origin cheese made with the milk from water buffalo raised in the marshlands of Campania and Lazio in a semi-wild state, or \"Mozzarella STG\", a cow's milk mozzarella. Neapolitan pizza is a Traditional Speciality Guaranteed product in Europe, and the art of its making is included on UNESCO's list of intangible cultural heritage. This style of pizza gave rise to the New York-style pizza that was first made by Italian immigrants to the United States in the early 20th century.",
// "Sicilian pizza is pizza prepared in a manner that originated in Sicily, Italy. Sicilian pizza is also known as sfincione or focaccia with toppings. This type of pizza became a popular dish in western Sicily by the mid-19th century and was the type of pizza usually consumed in Sicily until the 1860s. The version with tomatoes was not available prior to the 17th century. It eventually reached North America in a slightly altered form, with thicker crust and a rectangular shape. Traditional Sicilian pizza is often thick crusted and rectangular, but can also be round and similar to the Neapolitan pizza. It is often topped with onions, anchovies, tomatoes, herbs and strong cheese such as caciocavallo and toma. Other versions do not include cheese. The Sicilian methods of making pizza are linked to local culture and country traditions, so there are differences in preparing pizza among the Sicilian regions of Palermo, Catania, Siracusa and Messina.",
// "Chicago-style pizza is pizza prepared according to several different styles developed in Chicago. The most famous is the deep-dish pizza. The pan in which it is baked gives the pizza its characteristically high edge which provides ample space for large amounts of cheese and a chunky tomato sauce. Chicago-style pizza may be prepared in deep-dish style and as a stuffed pizza.",
// "Detroit-style pizza is a rectangular pizza with a thick crust that is crispy and chewy. It is traditionally topped with tomato sauce and Wisconsin brick cheese that goes all the way to the edges. This style of pizza is often baked in rectangular steel trays designed for use as automotive drip pans or to hold small industrial parts in factories. The style was developed during the mid-twentieth century in Detroit before spreading to other parts of the United States in the 2010s. The dish is one of Detroit's iconic local foods.",
// ""
// )
.parTraverse(...) は内部でファイバーを作成して IO のアクションを並列実行する。並列な IO ができたところで、Ref を使ってみてスレッド安全性を試してみよう。
import cats.effect.Ref
def appendCharCount(httpClient: Client[IO], q: String, ref: Ref[IO, List[(String, Int)]]): IO[Unit] =
for {
s <- search(httpClient, q)
_ <- ref.update(((q, s.size)) :: _)
} yield ()
{
import cats.effect.unsafe.implicits.global
val program = withHttpClient { httpClient =>
val xs = List("New York", "Neapolitan", "Sicilian", "Chicago", "Detroit", "London")
for {
r <- Ref[IO].of(Nil: List[(String, Int)])
_ <- xs.parTraverse(appendCharCount(httpClient, _, r))
x <- r.get
} yield x
}
program.unsafeRunSync().reverse
}
// res2: List[(String, Int)] = List(
// ("Sicilian", 954),
// ("London", 0),
// ("Neapolitan", 806),
// ("Chicago", 376),
// ("New York", 731),
// ("Detroit", 530)
// )
ここでは、IO エフェクトの逐次合成と並列合成の両方を組み合わせている。
ApplicativeError
Scala にはエラー状態を表す方法が複数ある。Cats は、エラーの発生とエラーからのリカバリーを表す ApplicativeError という型クラスを提供する。
trait ApplicativeError[F[_], E] extends Applicative[F] {
def raiseError[A](e: E): F[A]
def handleErrorWith[A](fa: F[A])(f: E => F[A]): F[A]
def recover[A](fa: F[A])(pf: PartialFunction[E, A]): F[A] =
handleErrorWith(fa)(e => (pf.andThen(pure(_))).applyOrElse(e, raiseError[A](_)))
def recoverWith[A](fa: F[A])(pf: PartialFunction[E, F[A]]): F[A] =
handleErrorWith(fa)(e => pf.applyOrElse(e, raiseError))
}
ApplicativeError としての Either
import cats._, cats.syntax.all._
{
val F = ApplicativeError[Either[String, *], String]
F.raiseError("boom")
}
// res0: Either[String, Nothing] = Left(value = "boom")
{
val F = ApplicativeError[Either[String, *], String]
val e = F.raiseError("boom")
F.recover(e) {
case "boom" => 1
}
}
// res1: Either[String, Int] = Right(value = 1)
エラー型の Throwable とハッピーな状態の型 A が入れ替わる try-catch と違って、ApplicativeError は E も A もデータとして保持しなければいけないことに注目してほしい。
ApplicativeError としての scala.util.Try
import scala.util.Try
{
val F = ApplicativeError[Try, Throwable]
F.raiseError(new RuntimeException("boom"))
}
// res2: Try[Nothing] = Failure(exception = java.lang.RuntimeException: boom)
{
val F = ApplicativeError[Try, Throwable]
val e = F.raiseError(new RuntimeException("boom"))
F.recover(e) {
case _: Throwable => 1
}
}
// res3: Try[Int] = Success(value = 1)
ApplicativeError としての IO
IO はファイバー内で走る必要があるので、scala.util.Try と Future のようにエラー状態を捕捉することができる。
import cats.effect.IO
{
val F = ApplicativeError[IO, Throwable]
F.raiseError(new RuntimeException("boom"))
}
// res4: IO[Nothing] = Error(t = java.lang.RuntimeException: boom)
{
val F = ApplicativeError[IO, Throwable]
val e = F.raiseError(new RuntimeException("boom"))
val io: IO[Int] = F.recover(e) {
case _: Throwable => 1
}
}
MonadCancel
Cats Effect の興味深いところは、それが Ref や IO などのデータ型を提供するライブラリであることと同時に、それは関数型エフェクトは何を意味するのかという型クラスを提供するライブラリでもあることだ。
MonadCancel は基盤となる型クラスで、MonadError (ApplicativeError のモナド版) を拡張し、キャンセル、マスキング (キャンセルの抑制)、ファイナライズをサポートする。関数型的な try-catch-finally だと考えることができる。
trait MonadCancel[F[_], E] extends MonadError[F, E] {
def rootCancelScope: CancelScope
def forceR[A, B](fa: F[A])(fb: F[B]): F[B]
def uncancelable[A](body: Poll[F] => F[A]): F[A]
def canceled: F[Unit]
def onCancel[A](fa: F[A], fin: F[Unit]): F[A]
def bracket[A, B](acquire: F[A])(use: A => F[B])(release: A => F[Unit]): F[B] =
bracketCase(acquire)(use)((a, _) => release(a))
def bracketCase[A, B](acquire: F[A])(use: A => F[B])(
release: (A, Outcome[F, E, B]) => F[Unit]): F[B] =
bracketFull(_ => acquire)(use)(release)
def bracketFull[A, B](acquire: Poll[F] => F[A])(use: A => F[B])(
release: (A, Outcome[F, E, B]) => F[Unit]): F[B]
}
MonadCancel としての IO
MonadCancelの非常にユニークな点は、自己キャンセルできることだ。
import cats._, cats.syntax.all._
import cats.effect.IO
lazy val program = IO.canceled >> IO.println("nope")
scala> {
import cats.effect.unsafe.implicits.global
program.unsafeRunSync()
}
java.util.concurrent.CancellationException: Main fiber was canceled
at cats.effect.IO.$anonfun$unsafeRunAsync$1(IO.scala:640)
at cats.effect.IO.$anonfun$unsafeRunFiber$2(IO.scala:702)
at scala.runtime.java8.JFunction0$mcV$sp.apply(JFunction0$mcV$sp.scala:18)
at cats.effect.kernel.Outcome.fold(Outcome.scala:37)
at cats.effect.kernel.Outcome.fold$(Outcome.scala:35)
at cats.effect.kernel.Outcome$Canceled.fold(Outcome.scala:181)
at cats.effect.IO.$anonfun$unsafeRunFiber$1(IO.scala:708)
at cats.effect.IO.$anonfun$unsafeRunFiber$1$adapted(IO.scala:698)
at cats.effect.CallbackStack.apply(CallbackStack.scala:45)
at cats.effect.IOFiber.done(IOFiber.scala:894)
at cats.effect.IOFiber.asyncCancel(IOFiber.scala:941)
at cats.effect.IOFiber.runLoop(IOFiber.scala:458)
at cats.effect.IOFiber.execR(IOFiber.scala:1117)
at cats.effect.IOFiber.run(IOFiber.scala:125)
at cats.effect.unsafe.WorkerThread.run(WorkerThread.scala:358)
もう少し落ち着いたバージョン:
{
import cats.effect.unsafe.implicits.global
program.unsafeRunAndForget()
}
いずれにせよ、エフェクトはキャンセルされ、"nope" というアクションは起きなかった。
キャンセルという概念そのものも IO データ型の中にスクリプト化されていることに注目してほしい。これは、Monix の Task が、CancelableFuture に対して行われ、いわゆる「世界の最後」の後に起こるのと対照的だ。
F.uncancelable
タイミング的に突然キャンセルされると不便なこともあるので、MonadCancel は uncancelable リージョンを提供し、このように使うことができる:
lazy val program2 = IO.uncancelable { _ =>
IO.canceled >> IO.println("important")
}
scala> {
import cats.effect.unsafe.implicits.global
program2.unsafeRunSync()
}
important
IO.uncancelable { ... } 内部では、キャンセルは無視される。再びキャンセルを有効にするためには渡された poll 関数を使う:
lazy val program3 = IO.uncancelable { poll =>
poll(IO.canceled) >> IO.println("nope again")
}
scala> {
import cats.effect.unsafe.implicits.global
program3.unsafeRunSync()
}
java.util.concurrent.CancellationException: Main fiber was canceled
....
IO.uncancelable { ... } リージョンは低レベルAPI で直接使うことは少ないと思う。
bracket
リソース安全なコード書くためには、キャンセルと例外の両方の対応をする必要がある。
import cats.effect.MonadCancel
lazy val program4 = MonadCancel[IO].bracket(IO.pure(0))(x =>
IO.raiseError(new RuntimeException("boom")))(_ =>
IO.println("cleanup"))
scala> {
import cats.effect.unsafe.implicits.global
program4.unsafeRunSync()
}
cleanup
java.lang.RuntimeException: boom
....
MonadCancel[IO].bracket を使うことで、cleanup コードが走ることが保証される。
今日はここまで。
19 日目
18日目には John Launchbury さんと Simon Peyton-Jones さんの Lazy Functional State Threads を少し見ながらエフェクトシステムの一例として Cats Effect を見始めた。
とりあえず IO データ型が逐次的にも並列的にも合成することができるプログラムを記述できることが分かった。
FunctionK
Cats は 2つの型コンストラクタ F1[_] と F2[_] を型パラメータとして受け取り、全ての A において F1[A] の全ての値を F2[A] に変換することができることを表す FunctionK を提供する。
trait FunctionK[F[_], G[_]] extends Serializable { self =>
/**
* Applies this functor transformation from `F` to `G`
*/
def apply[A](fa: F[A]): G[A]
def compose[E[_]](f: FunctionK[E, F]): FunctionK[E, G] =
new FunctionK[E, G] { def apply[A](fa: E[A]): G[A] = self(f(fa)) }
def andThen[H[_]](f: FunctionK[G, H]): FunctionK[F, H] =
f.compose(self)
def or[H[_]](h: FunctionK[H, G]): FunctionK[EitherK[F, H, *], G] =
new FunctionK[EitherK[F, H, *], G] { def apply[A](fa: EitherK[F, H, A]): G[A] = fa.fold(self, h) }
....
}
シンボルを使って FunctionK[F1, F2] は F1 ~> F2 と表記される:
import cats._, cats.syntax.all._
lazy val first: List ~> Option = ???
F[_] のことをファンクター (函手) と呼ぶことが多いので、FunctionK も中二病的に「自然変換」と呼ばれることがあるが、FunctionK ぐらいの名前のほうが実態に即していると思う。
最初の要素を返す List ~> Option を実装してみよう。
val first: List ~> Option = new (List ~> Option) {
def apply[A](fa: List[A]): Option[A] = fa.headOption
}
// first: List ~> Option = repl.MdocSession1@27f549c
first(List("a", "b", "c"))
// res1: Option[String] = Some(value = "a")
少し冗長に見える。このようなコードをどれだけ頻繁に書くかにもよるが、普通の関数が以下のように短く書けるように簡易記法があると嬉しい:
import scala.util.chaining._
List("a", "b", "c").pipe(_.headOption)
// res2: Option[String] = Some(value = "a")
kind projector が提供する「多相ラムダ書き換え」(polymorphic lambda rewrite) λ を使うとこう書ける:
val first = λ[List ~> Option](_.headOption)
// first: AnyRef with List ~> Option = repl.MdocSession2@73fd8cf6
first(List("a", "b", "c"))
// res4: Option[String] = Some(value = "a")
Higher-Rank Polymorphism in Scala
2010年の7月に Rúnar (@runarorama) さんが Higher-Rank Polymorphism in Scala というブログ記事を書いてランク2多相性を解説した。吉田さんが 2012年に Scala での高ランクポリモーフィズムとして和訳している。まずは、通常の (ランク1) 多相関数をみてみる:
def pureList[A](a: A): List[A] = List(a)
これはどの A に対しても動く:
pureList(1)
// res5: List[Int] = List(1)
pureList("a")
// res6: List[String] = List("a")
Rúnar さんが 2010年に指摘したのは、Scala にはこれにに対するファーストクラス概念が無いということだ。
この関数を別の関数の引数にしたいとします。ランク1多相では、これは不可能です
def usePolyFunc[A, B](f: A => List[A], b: B, s: String): (List[B], List[String]) =
(f(b), f(s))
// error: type mismatch;
// found : b.type (with underlying type B)
// required: A
// (f(b), f(s))
// ^
// error: type mismatch;
// found : s.type (with underlying type String)
// required: A
// (f(b), f(s))
// ^
これは Launchbury さんと SPJ が 1994年に State Threads で Haskell ができないと指摘したのと同じことだ:
runST :: ∀a. (∀s. ST s a) -> a
This is not a Hindley-Milner type, because the quantifiers are not all at the top level; it is an example of rank-2 polymorphism.
Rúnar さんに戻ると:
BとStringはAではないので、これは型エラーになります。つまり、型Aは[A, B]のBに固定されてしまいます。 私達が本当に欲しいのは、引数に対して多相的な関数です。もし仮に Scala にランクN型があるとすれば以下のようになるでしょう
def usePolyFunc[B](f: (A => List[A]) forAll { A }, b: B, s: String): (List[B], List[String]) =
(f(b), f(s))
ランク2多相な関数をあらわすために、
applyメソッドに型引数をとる新しい trait をつくります。
trait ~>[F[_], G[_]] {
def apply[A](a: F[A]): G[A]
}
これは FunctionK と同じ、正確には FunctionK は ~> だと言うべきだろうか。次に巧みな技で Rúnar さんは Id データ型を使って A を F[_] へと持ち上げている:
identity functor から List functor の自然変換 (natural transformation) によって、(最初に例に出した)リストにある要素を加える関数をあらわすことができるようになりました:
val pureList: Id ~> List = λ[Id ~> List](List(_))
// pureList: Id ~> List = repl.MdocSession3@444e9bf4
def usePolyFunc[B](f: Id ~> List, b: B, s: String): (List[B], List[String]) =
(f(b), f(s))
usePolyFunc(pureList, 1, "x")
// res9: (List[Int], List[String]) = (List(1), List("x"))
できた。これで頑張って多相関数を別の関数に渡せるようになった。一時期ランク2型多相が一部で大人気だった気がするが、これは State Threads やその他の後続の論文にてリソースに対する型安全なアクセスを保証する基礎だと喧伝されていたからじゃないだろうか。
MonadCancel での FunctionK
MonadCancel をもう一度見てみると、FunctionK が隠れている:
trait MonadCancel[F[_], E] extends MonadError[F, E] {
def rootCancelScope: CancelScope
def forceR[A, B](fa: F[A])(fb: F[B]): F[B]
def uncancelable[B](body: Poll[F] => F[B]): F[B]
....
}
上の Poll[F] というのは実は、F ~> F の型エイリアスだからだ:
trait Poll[F[_]] extends (F ~> F)
つまり、全ての A に対して、F[A] は F[A] を返す。
import cats.effect.IO
lazy val program = IO.uncancelable { poll =>
poll(IO.canceled) >> IO.println("nope again")
}
上のような状況で IO は全ての A において動く関数を僕たちに渡す必要があるが、Rúnar さんの解説によってランク1多相だとそれが不可能なことが分かったはずだ。例えば仮に以下のような定義だとする:
def uncancelable[A, B](body: F[A] => F[A] => F[B]): F[B]
これは poll(...) が 1回呼び出される場合なら何とかなるかもしれないが、IO.uncancelable { ... } 内からは poll(...) は複数回呼んでもいいはずだ:
lazy val program2: IO[Int] = IO.uncancelable { poll =>
poll(IO.println("a")) >> poll(IO.pure("b")) >> poll(IO.pure(1))
}
なので、poll(...) は実際には ∀A. IO[A] => IO[A]、つまり IO ~> IO だ。
Resource データ型
Rúnar さんは Higher-Rank Polymorphism in Scala を以下のように締めくくった:
これ (ランク2多相) を使えば、Lightweight Monadic Regions で説明されている SIO monad のような、静的に保証された安全なリソースへのアクセスができるだろうか。
Cats Effect は Resource データ型を提供し、これは Oleg Kiselyov さんと Chung-chieh Shan さんの Lightweight Monadic Regions みたいに使えるかもしれない。18日目に見た MonadCancel をデータ型としてエンコードしたものだ。
Resourceを構築する最も簡易な方法はResource.makeで、最も簡易にリソースを使う方法はResource#useだ。任意のアクションをResource.evalを使って持ち上げることもできる:
object Resource {
def make[F[_], A](acquire: F[A])(release: A => F[Unit]): Resource[F, A]
def eval[F[_], A](fa: F[A]): Resource[F, A]
def fromAutoCloseable[F[_], A <: AutoCloseable](acquire: F[A])(
implicit F: Sync[F]): Resource[F, A] =
Resource.make(acquire)(autoCloseable => F.blocking(autoCloseable.close()))
}
sealed abstract class Resource[F[_], +A] {
def use[B](f: A => F[B]): F[B]
}
実践に基づいた具体例を見ていこう:
- 読み込み用に 2つのファイルを開き、ただし、片方を設定ファイルとする。
- 設定ファイルから出力用ファイル名 (ログファイルなど) を読む。
- 出力用ファイルを開いて、読み込みファイルの内容を交互に書き出す。
- 設定ファイルを閉じる。
- 別の読み込み用のファイルの残りの内容を出力用ファイルに書き出す。
以下はテキストファイルの最初の行を読み込むプログラムだ:
import cats._, cats.syntax.all._
import cats.effect.{ IO, MonadCancel, Resource }
import java.io.{ BufferedReader, BufferedWriter }
import java.nio.charset.StandardCharsets
import java.nio.file.{ Files, Path, Paths }
def bufferedReader(path: Path): Resource[IO, BufferedReader] =
Resource.fromAutoCloseable(IO.blocking {
Files.newBufferedReader(path, StandardCharsets.UTF_8)
})
.onFinalize { IO.println("closed " + path) }
lazy val program: IO[String] = {
val r0 = bufferedReader(Paths.get("docs/19/00.md"))
r0 use { reader0 =>
IO.blocking { reader0.readLine }
}
}
scala> {
import cats.effect.unsafe.implicits._
program.unsafeRunSync()
}
closed docs/19/00.md
val res0: String = ---
以下は、テキストをファイルに書き込むプログラムだ:
def bufferedWriter(path: Path): Resource[IO, BufferedWriter] =
Resource.fromAutoCloseable(IO.blocking {
Files.newBufferedWriter(path, StandardCharsets.UTF_8)
})
.onFinalize { IO.println("closed " + path) }
lazy val program2: IO[Unit] = {
val w0 = bufferedWriter(Paths.get("/tmp/Resource.txt"))
w0 use { writer0 =>
IO.blocking { writer0.write("test\n") }
}
}
{
import cats.effect.unsafe.implicits._
program2.unsafeRunSync()
}
これは /tmp/Resource.txt という名前のテキストファイルを作成した。ここまではリソース管理的には些細なことしかしていない。Oleg さんと Chung-chieh Shan さんが提示した問題文は、ログファイルの名前は設定ファイルから読み出すが、ログファイルの方が設定ファイルのライフサイクルよりも長生きする必要があるのでより複雑だ。
def inner(input0: BufferedReader, config: BufferedReader): IO[(BufferedWriter, IO[Unit])] = for {
fname <- IO.blocking { config.readLine }
w0 = bufferedWriter(Paths.get(fname))
// do the unsafe allocated
p <- w0.allocated
(writer0, releaseWriter0) = p
_ <- IO.blocking { writer0.write(fname + "\n") }
- <-
(for {
l0 <- IO.blocking { input0.readLine }
_ <- IO.blocking { writer0.write(l0 + "\n") }
l1 <- IO.blocking { config.readLine }
_ <- IO.blocking { writer0.write(l1 + "\n") }
} yield ()).whileM_(IO.blocking { input0.ready && config.ready })
} yield (writer0, releaseWriter0)
lazy val program3: IO[Unit] = {
val r0 = bufferedReader(Paths.get("docs/19/00.md"))
r0 use { input0 =>
MonadCancel[IO].bracket({
val r1 = bufferedReader(Paths.get("src/main/resources/a.conf"))
r1 use { config => inner(input0, config) }
})({ case (writer0, _) =>
(for {
l0 <- IO.blocking { input0.readLine }
_ <- IO.blocking { writer0.write(l0 + "\n") }
} yield ()).whileM_(IO.blocking { input0.ready })
})({
case (_, releaseWriter0) => releaseWriter0
})
}
}
ログファイルを閉じるのを避けるために Resource#allocated メソッドを使って、その代わりに後で絶対に閉じられることが保証されるように MonadCancel[IO].bracket を使った。走らせるとこのようになる:
scala> {
import cats.effect.unsafe.implicits._
program3.unsafeRunSync()
}
closed src/main/resources/a.conf
closed /tmp/zip_test.txt
closed docs/19/00.md
設定ファイルが最初に閉じられているのが分かる。
少しズルをして例題を実装することができたが、Resource の柔軟性を示すことができたと思う。
モナドとしての Resource
program3 は少しややこしくなったが、複数のリソースをまとめて取得して、まとめて解放したい場合がほとんどだと思う。
lazy val program4: IO[String] = (
for {
r0 <- bufferedReader(Paths.get("docs/19/00.md"))
r1 <- bufferedReader(Paths.get("src/main/resources/a.conf"))
w1 <- bufferedWriter(Paths.get("/tmp/zip_test.txt"))
} yield (r0, r1, w1)
).use { case (intput0, config, writer0) =>
IO.blocking { intput0.readLine }
}
{
import cats.effect.unsafe.implicits._
program4.unsafeRunSync()
}
// res1: String = "---"
上の例では、複数のリソースがもモナディックに組み合わされて、use されている。
Resource のキャンセル対応
use 中でもリソースがちゃんとキャンセル対応できるのかを確かめるために、. を永遠と表示するデモアプリを作って Ctrl-C でキャンセルさせてみよう:
import cats._, cats.syntax.all._
import cats.effect.{ ExitCode, IO, IOApp, Resource }
import java.io.{ BufferedReader, BufferedWriter }
import java.nio.charset.StandardCharsets
import java.nio.file.{ Files, Path, Paths }
object Hello extends IOApp {
def bufferedReader(path: Path): Resource[IO, BufferedReader] =
Resource.fromAutoCloseable(IO.blocking {
Files.newBufferedReader(path, StandardCharsets.UTF_8)
})
.onFinalize { IO.println("closed " + path) }
override def run(args: List[String]): IO[ExitCode] =
program.as(ExitCode.Success)
lazy val program: IO[String] = (
for {
r0 <- bufferedReader(Paths.get("docs/19/00.md"))
r1 <- bufferedReader(Paths.get("src/main/resources/a.conf"))
} yield (r0, r1)
).use { case (intput0, config) =>
IO.print(".").foreverM
}
}
アプリを実行した結果こうなった:
$ java -jar target/scala-2.13/herding-cats-assembly-0.1.0-SNAPSHOT.jar
..................................................................................................................................................................................................................................................................................................................................................................................................................................................................................^C............................................................................................................................................................................................................................................closed src/main/resources/a.conf
closed docs/19/00.md
リソースがちゃんと閉じられているのが分かる。よくできました。
これは use { ... } 中に起こっているので、Resource が MonadCancel を形成するというのはちょっと違うことに注意してほしい。use の定義を見ると理解が深まるかもしれない:
/**
* Allocates a resource and supplies it to the given function.
* The resource is released as soon as the resulting `F[B]` is
* completed, whether normally or as a raised error.
*
* @param f the function to apply to the allocated resource
* @return the result of applying [F] to
*/
def use[B](f: A => F[B])(implicit F: MonadCancel[F, Throwable]): F[B] =
fold(f, identity)
この場合、Ctrl-C は IO が処理していて、use { ... } は f が失敗したときでもリソースが解放されることを保証しているんだと思う。
モナドトランスフォーマーとしての Ref
Ref や Resource といったデータ型は何か変わっている事がある:
abstract class Ref[F[_], A] extends RefSource[F, A] with RefSink[F, A] {
/**
* Modifies the current value using the supplied update function. If another modification
* occurs between the time the current value is read and subsequently updated, the modification
* is retried using the new value. Hence, `f` may be invoked multiple times.
*
* Satisfies:
* `r.update(_ => a) == r.set(a)`
*/
def update(f: A => A): F[Unit]
def modify[B](f: A => (A, B)): F[B]
....
}
Option などが受け取るような型パラメータ A の他に、Ref は F[_] でパラメータ化されている。
scala> :k -v cats.effect.Ref
cats.effect.Ref's kind is X[F[A1],A2]
(* -> *) -> * -> *
This is a type constructor that takes type constructor(s): a higher-kinded type.
これらはエフェクト型 F を受け取るモナドトランスフォーマーだと言える。SyncIO といった別の F を渡すことも可能だ:
import cats._, cats.syntax.all._
import cats.effect.{ IO, Ref, SyncIO }
lazy val program: SyncIO[Int] = for {
r <- Ref[SyncIO].of(0)
x <- r.get
} yield x
モナドトランスフォーマーとしての Resource
ということはリソースも F[_] を使ってパラメトリックにすることができる:
import cats.effect.{ IO, MonadCancel, Resource, Sync }
import java.io.BufferedReader
import java.nio.charset.{ Charset, StandardCharsets }
import java.nio.file.{ Files, Path, Paths }
def bufferedReader[F[_]: Sync](path: Path, charset: Charset): Resource[F, BufferedReader] =
Resource.fromAutoCloseable(Sync[F].blocking {
Files.newBufferedReader(path, charset)
})
lazy val r0: Resource[SyncIO, BufferedReader] = bufferedReader[SyncIO](Paths.get("/tmp/foo"), StandardCharsets.UTF_8)
モナドトランスフォーマーのほとんどは FunctionK を受け取る mapK(...) というメソッドがあって、別の G[_] へと変換することができる。1つのエフェクト型から別のエフェクト型への ~> を定義できれば、リソースも変換することができる。これはかなり衝撃的だ:
lazy val toIO = λ[SyncIO ~> IO](si => IO.blocking { si.unsafeRunSync() })
lazy val r1: Resource[IO, BufferedReader] = r0.mapK(toIO)
今日はここまで。