圏としてのモノイド 

Awodey:

モノイド (単位元を持つ半群とも呼ばれる) は、集合 M で、二項演算 ·: M × M => M と特定の「単位元」(unit) u ∈ M を持ち、任意の x, y, z ∈ M に対して以下の条件を満たすもの:

• x · (y · z) = (x · y) · z
• u · x = x = x · u

同義として、モノイドは唯一つの対象を持つ圏である。その圏の射はモノイドの要素だ。特に恒等射は単位元 u である。射の合成はモノイドの二項演算 m · n だ。

モノイドが Cats でどうエンコードされるかは 4日目の Monoid) をみてほしい。

trait Monoid[@sp(Int, Long, Float, Double) A] extends Any with Semigroup[A] {
  def empty: A

  ....
}

trait Semigroup[@sp(Int, Long, Float, Double) A] extends Any with Serializable {
  def combine(x: A, y: A): A

  ....
}

Int と 0 の加算は以下のように書ける:

scala> 10 |+| Monoid[Int].empty
res26: Int = 10

このモノイドがただ一つの対象を持つ圏という考え方は「何を言っているんだ」と前は思ったものだけど、単集合を見ているので今なら理解できる気がする。

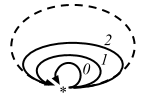
ここで注意してほしいのは、上の (Int, +) モノイドにおいては、射は文字通り 0、1、2 などであって関数ではないということだ。

Mon 

モノイドに関連する圏がもう一つある。 モノイドとモノイドの構造を保存した関数の圏は Mon と表記される。このような構造を保存する射は準同型写像 (homomorphism) と呼ばれる。

モノイド M からモノイド N への準同型写像は、関数 h: M => N で全ての m, n ∈ M について以下の条件を満たすも

• h(m ·_M n) = h(m) ·_N h(n)
• h(u_M) = u_N

それぞれのモノイドは圏なので、モノイド準同型写像 (monoid homomorphism) は函手 (functor) の特殊形だと言える。