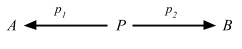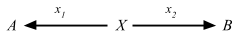Products
Let us begin by considering products of sets. Given sets A and B, the cartesian product of A and B is the set of ordered pairs
A × B = {(a, b)| a ∈ A, b ∈ B}
There are two coordinate projections:
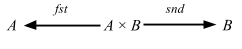
with:
- fst ∘ (a, b) = a
- snd ∘ (a, b) = b
This notion of product relates to scala.Product, which is the base trait for all tuples and case classes.
For any element in c ∈ A × B, we have c = (fst ∘ c, snd ∘ c)
Using the same trick as yesterday, we can introduce the singleton explicitly:
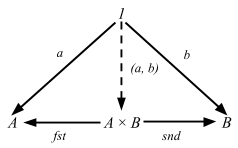
The (external) diagram captures what we stated in the above. If we replace 1-elements by generalized elements, we get the categorical definition.
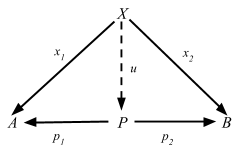
Definition 2.15. In any category C, a product diagram for the objects A and B consists of an object P and arrows p1 and p2
satisfying the following UMP:Given any diagram of the form
there exists a unique u: X => P, making the diagram
commute, that is, such that x1 = p1 u and x2 = p2 u.
Because this is universal, this applies to any category.
Uniqueness of products
UMP also suggests that all products of A and B are unique up to isomorphism.
Proposition 2.17 Products are unique up to isomorphism.
Suppose we have P and Q that are products of objects A and B.
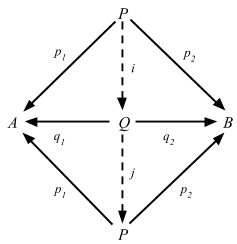
- Because P is a product, there is a unique i: P => Q such that p1 = q1 ∘ i and p2 = q2 ∘ i
- Because Q is a product, there is a unique j: Q => P such that q1 = p1 ∘ j and q2 = p2 ∘ j
- By composing j and i we get 1P = j ∘ i
- Similarly, we can also get 1Q = i ∘ j
- Thus i is an isomorphism, and P ≅ Q ∎
Since all products are isometric, we can just denote one as A × B, and the arrow u: X => A × B is denoted as ⟨x1, x2⟩.
Examples
We saw that in Sets, cartesian product is a product.
Let P be a poset and consider a product of elements p, q ∈ P. We must have projections
- p × q ≤ p
- p × q ≤ q
and if for any element x, x ≤ p, and x ≤ q
then we need
- x ≤ p × q
In this case, p × q becomes greatest lower bound.