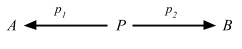Hom-sets
We need to pick up some of the fundamentals that I skipped over.
Large, small, and locally small
Definition 1.11. A category C is called small if both the collection C0 of objects of C and the collection C1 of arrows of C are sets. Otherwise, C is called large.
For example, all finite categories are clearly small, as is the category Setsfin of finite sets and functions.
Cat is actually a category of all small categories, so Cat doesn’t contain itself.
Definition 1.12. A category C is called locally small if for all objects X, Y in C, the collection HomC(X, Y) = { f ∈ C1 | f: X = Y } is a set (called a hom-set)
Hom-sets
A Hom-set Hom(A, B) is a set of arrows between objects A and B. Hom-sets are useful because we can use it to inspect (look into the elements) an object using just arrows.
Putting any arrow f: A => B in C into Hom(X, A) would create a function:
- Hom(X, f): Hom(X, A) => Hom(X, B)
- case x => (f ∘ x: X => A => B)
Thus, Hom(X, f) = f ∘ _.
By using the singleton trick in Sets, we can exploit A ≅ HomSets(1, A). If we generalize this we can think of Hom(X, A) as a set of generalized elements from X.
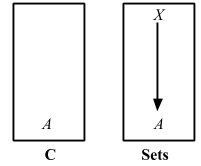
We can then create a functor out of this by replacing A with _
Hom(X, _): C => Sets.
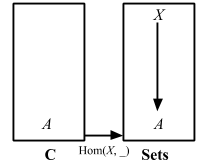
This functor is called the representable functor, or covariant hom-functor.
Thinking in Hom-set
For any object P, a pair of arrows p1: P => A and p2: P => B determine an element (p1, p2) of the set
Hom(P, A) × Hom(P, B).
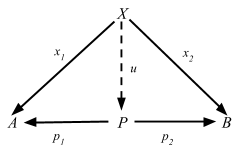
We see that given x: X => P we can derive x1 and x2 by composing with p1 and p2 respectively. Because compositions are functions in Hom sets, we could express the above as a function too:
ϑX = (Hom(X, p1), Hom(X, p2)): Hom(X, P) => Hom(X, A) × Hom(X, B)
where ϑX(x) = (x1, x2)
That’s a cursive theta, by the way.
Proposition 2.20. A diagram of the form
is a product for A and B iff for every object X, the canonical function ϑX given in (2.1) is an isomorphism,
ϑX: Hom(X, P) ≅ Hom(P, A) × Hom(P, B).
This is pretty interesting because we just replaced a diagram with an isomorphic equation.