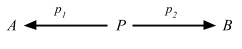Hom 集合 

飛ばした概念もあるので、少し前に戻る。

大きい圏、小さい圏、局所的に小さい圏 

定義 1.11. 任意の圏 C において、C の対象の集まり C₀ と、C の射の集まり C₁ が集合であるとき、小さい圏という。その他の場合は、C は大きいという。

例えば、全ての有限圏は明らかに小さいが、有限集合と関数の圏である Sets_fin も小さい。

Cat は、実は全ての小さい圏の圏であるため、Cat は自身を含まない。

定義 1.12. 任意の圏 C は、C の全ての対象 X と Y について、Hom_C(X, Y) = { f ∈ C₁ | f: X = Y } という集まりが集合であるとき、局所的に小さいといい、これを hom集合という。

Hom集合 

Hom集合 (Hom-set) は Hom(A, B) と表記され、対象 A と B の射の集合だ。Hom集合は対象を射だけを使って検査 (要素を見ること) することができるため、役に立つ。

C の任意の射 f: A => B を Hom(X, A) に入れると関数が得られる:

• Hom(X, f): Hom(X, A) => Hom(X, B)
• case x => (f ∘ x: X => A => B)

つまり、Hom(X, f) = f ∘ _ となる。

Sets 圏で単集合のトリックを使うことで、A ≅ Hom_Sets(1, A) であることを利用できる。これを一般化すると、Hom(X, A) は、X から見た generalized element の集合だと考えることができる。

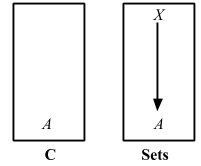
A を _ で置換することで函手を作ることができる
> Hom(X, _): C => Sets.

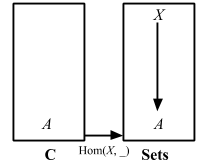
この函手は representable functor または共変Hom函手と呼ばれる。

Hom集合で考える 

任意の対象 P について、射のペア p₁: P => A と p₂: P => B によって集合
Hom(P, A) × Hom(P, B)
の要素 (p₁, p₂) を決定することができる。

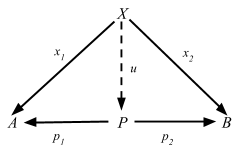
上の図式によって、x: X => P が与えられれば、それを p₁ と p₂ に合成することによって、それぞれ x₁ と x₂ が得られることが分かる。射の合成は Hom集合では関数であるため、これも関数として書くことができる:

ϑ_X = (Hom(X, p₁), Hom(X, p₂)): Hom(X, P) => Hom(X, A) × Hom(X, B)
ただし ϑ_X(x) = (x₁, x₂)

命題 2.20. 以下の形式の図式

は、全ての対象 X に関して、(2.1) で与えられるカノニカル関数 ϑ_X が同型
ϑ_X: Hom(X, P) ≅ Hom(P, A) × Hom(P, B)
であり、その時に限り、A と B の積である。

これは図式を同型等式で入れ替えることができたという意味で興味深い。