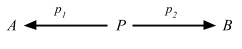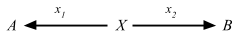積
まずは集合の積を考える。集合 A と B があるとき、A と B のデカルト積は順序対 (ordered pairs) の集合となる
A × B = {(a, b)| a ∈ A, b ∈ B}
2つの座標射影 (coordinate projection) があって
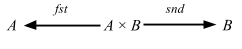
これは以下の条件を満たす:
- fst ∘ (a, b) = a
- snd ∘ (a, b) = b
この積という考えは case class やタプルの基底 trait である scala.Product にも関連する。
任意の要素 c ∈ A × B に対して、c = (fst ∘ c, snd ∘ c) ということができる。
昨日と同じトリックを使って、明示的に単集合を導入する:
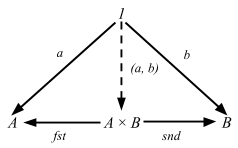
この(外部)図式は上の条件を捕捉している。ここで 1-要素を一般化すると圏論的定義が得られる。
定義 2.15. 任意の圏 C において、対象 A と B の積の図式は対象 P と射 p1 と p2 から構成され
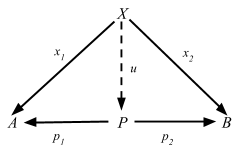
以下の UMP を満たす:この形となる任意の図式があるとき
次の図式
が可換となる (つまり、x1 = p1 u かつ x2 = p2 u が成立する) 一意の射 u: X => P が存在する。
この定義は普遍であるため、任意の圏に適用することができる。
積の一意性
普遍性は A と B の積の全てが同型を除いて一意であることも示唆する。
命題 2.17 積は同型を除いて一意である。
P と Q が対象 A と B の積であるとする。
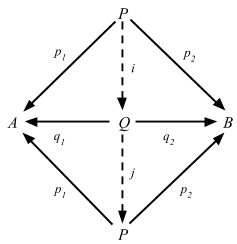
- P は積であるため、p1 = q1 ∘ i かつ p2 = q2 ∘ i を満たす一意の i: P => Q が存在する。
- Q は積であるため、q1 = p1 ∘ j かつ q2 = p2 ∘ j を満たす一意の j: Q => P が存在する。
- i と j を合成することで 1P = j ∘ i が得られる。
- 同様にして 1Q = i ∘ j。
- i は同型射、P ≅ Q である。∎
全ての積は同型であるため、一つを取って A × B と表記する。また、射 u: X => A × B は ⟨x1, x2⟩ と表記する。
例
Sets 圏ではデカルト積が積となることは紹介した。
P が poset だとして、要素 p, q ∈ P の積を考える。以下のような射影が必要なる
- p × q ≤ p
- p × q ≤ q
そして任意の要素 x で x ≤ p かつ x ≤ q であるものに対しては
- x ≤ p × q
を満たす必要がある。
この場合 p × q は最大下限 (greatest lower bound) となる。