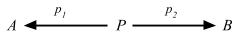Coproducts
One of the well known dual concepts is coproduct, which is the dual of product. Prefixing with “co-” is the convention to name duals.
Here’s the definition of products again:
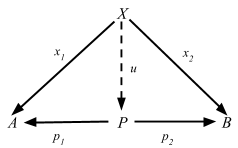
Definition 2.15. In any category C, a product diagram for the objects A and B consists of an object P and arrows p1 and p2
satisfying the following UMP:Given any diagram of the form
there exists a unique u: X => P, making the diagram
commute, that is, such that x1 = p1 u and x2 = p2 u.
Flip the arrows around, and we get a coproduct diagram:
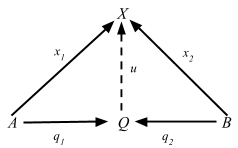
Since coproducts are unique up to isomorphism, we can denote the coproduct as A + B, and [f, g] for the arrow u: A + B => X.
The “coprojections” i1: A => A + B and i2: B => A + B are usually called injections, even though they need not be “injective” in any sense.
Similar to the way products related to product type encoded as scala.Product, coproducts relate to the notion of sum type, or union type, like this:
data TrafficLight = Red | Yellow | Green
Unboxed union types
Using case class and sealed traits as encoding for this doesn’t work well in some cases like if I wanted a union of Int and String. An interesting read on this topic is Miles Sabin (@milessabin)’s Unboxed union types in Scala via the Curry-Howard isomorphism.
Everyone’s seen De Morgan’s law:
!(A || B) <=> (!A && !B)
Since Scala has conjunction via A with B, Miles discovered that we can get disjunction if we can encode negation. This is ported to Scalaz under scalaz.UnionTypes:
trait UnionTypes {
type ![A] = A => Nothing
type !![A] = ![![A]]
trait Disj { self =>
type D
type t[S] = Disj {
type D = self.D with ![S]
}
}
type t[T] = {
type t[S] = (Disj { type D = ![T] })#t[S]
}
type or[T <: Disj] = ![T#D]
type Contains[S, T <: Disj] = !![S] <:< or[T]
type ∈[S, T <: Disj] = Contains[S, T]
sealed trait Union[T] {
val value: Any
}
}
object UnionTypes extends UnionTypes
Let’s try implementing Miles’s size example:
scala> import UnionTypes._
import UnionTypes._
scala> type StringOrInt = t[String]#t[Int]
defined type alias StringOrInt
scala> implicitly[Int ∈ StringOrInt]
res0: scalaz.UnionTypes.∈[Int,StringOrInt] = <function1>
scala> implicitly[Byte ∈ StringOrInt]
<console>:18: error: Cannot prove that Byte <:< StringOrInt.
implicitly[Byte ∈ StringOrInt]
^
scala> def size[A](a: A)(implicit ev: A ∈ StringOrInt): Int = a match {
case i: Int => i
case s: String => s.length
}
size: [A](a: A)(implicit ev: scalaz.UnionTypes.∈[A,StringOrInt])Int
scala> size(23)
res2: Int = 23
scala> size("foo")
res3: Int = 3
\/
Scalaz also has \/, which could be thought of as a form of sum type. The symbolic name \/ kind of makes sense since ∨ means the logical disjunction. This was covered in day 7: \/. We can rewrite the size example as follows:
scala> def size(a: String \/ Int): Int = a match {
case \/-(i) => i
case -\/(s) => s.length
}
size: (a: scalaz.\/[String,Int])Int
scala> size(23.right[String])
res15: Int = 23
scala> size("foo".left[Int])
res16: Int = 3
Coproduct and Inject
There is actually Coproduct in Scalaz, which is like an Either on type constructor:
final case class Coproduct[F[_], G[_], A](run: F[A] \/ G[A]) {
...
}
object Coproduct extends CoproductInstances with CoproductFunctions
trait CoproductFunctions {
def leftc[F[_], G[_], A](x: F[A]): Coproduct[F, G, A] =
Coproduct(-\/(x))
def rightc[F[_], G[_], A](x: G[A]): Coproduct[F, G, A] =
Coproduct(\/-(x))
...
}
In Data types à la carte Wouter Swierstra (@wouterswierstra) describes how this could be used to solve the so-called Expression Problem:
The goal is to define a data type by cases, where one can add new cases to the data type and new functions over the data type, without recompiling existing code, and while retaining static type safety.
The automatic injections described in this paper was contributed to Scalaz in #502 by @ethul. An example of how this could be used is available in his typeclass-inject’s README.
Individual expressions construct Free[F, Int] where F is the coproduct of all three algebras.