Natural Transformation 

I think we now have enough ammunition on our hands to tackle naturality. Let’s skip to the middle of the book, section 7.4.

A natural transformation is a morphism of functors. That is right: for fix categories C and D, we can regard the functors C => D as the object of a new category, and the arrows between these objects are what we are going to call natural transformations.

There are some interesting blog posts around natural transformation in Scala:

• Higher-Rank Polymorphism in Scala, Rúnar (@runarorama) July 2, 2010
• Type-Level Programming in Scala, Part 7: Natural transformation literals, Mark Harrah (@harrah) October 26, 2010
• First-class polymorphic function values in shapeless (2 of 3) — Natural Transformations in Scala, Miles Sabin (@milessabin) May 10, 2012

Mark presents a simple example of why we might want a natural transformation:

We run into problems when we proceed to natural transformations. We are not able to define a function that maps an Option[T] to List[T] for every T, for example. If this is not obvious, try to define toList so that the following compiles:

val toList = ...

val a: List[Int] = toList(Some(3))
assert(List(3) == a)

val b: List[Boolean] = toList(Some(true))
assert(List(true) == b)

In order to define a natural transformation M ~> N (here, M=Option, N=List), we have to create an anonymous class because Scala doesn’t have literals for quantified functions.

Scalaz ports this. Let’s see NaturalTransformation:

/** A universally quantified function, usually written as `F ~> G`,
  * for symmetry with `A => B`.
  * ....
  */
trait NaturalTransformation[-F[_], +G[_]] {
  self =>
  def apply[A](fa: F[A]): G[A]

  ....
}

The aliases are available in the package object for scalaz namespace:

  /** A [[scalaz.NaturalTransformation]][F, G]. */
  type ~>[-F[_], +G[_]] = NaturalTransformation[F, G]
  /** A [[scalaz.NaturalTransformation]][G, F]. */
  type <~[+F[_], -G[_]] = NaturalTransformation[G, F]

Let’s try defining toList:

scala> val toList = new (Option ~> List) {
         def apply[T](opt: Option[T]): List[T] =
           opt.toList
       }
toList: scalaz.~>[Option,List] = 1@2fdb237

scala> toList(3.some)
res17: List[Int] = List(3)

scala> toList(true.some)
res18: List[Boolean] = List(true)

If we compare the terms with category theory, in Scalaz the type constructors like List and Option support Functors which maps between two categories.

trait Functor[F[_]] extends InvariantFunctor[F] { self =>
  ////

  /** Lift `f` into `F` and apply to `F[A]`. */
  def map[A, B](fa: F[A])(f: A => B): F[B]
  ...
}

This is a much contrained representation of a functor compared to more general C => D, but it’s a functor if we think of the type constructors as categories.

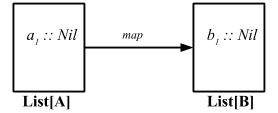
Since NaturalTransformation (~>) works at type constructor (first-order kinded type) level, it is an arrow between the functors (or a family of arrows between the categories).

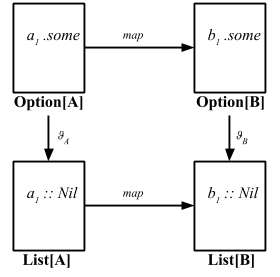
We’ll continue from here later.