learning Scalaz 

How many programming languages have been called Lisp in sheep’s clothing? Java brought in GC to familiar C++ like grammar. Although there have been other languages with GC, in 1996 it felt like a big deal because it promised to become a viable alternative to C++. Eventually, people got used to not having to manage memory by hand. JavaScript and Ruby both have been called Lisp in sheep’s clothing for their first-class functions and block syntax. The homoiconic nature of S-expression still makes Lisp-like languages interesting as it fits well to macros.

Recently languages are borrowing concepts from newer breed of functional languages. Type inference and pattern matching I am guessing goes back to ML. Eventually people will come to expect these features too. Given that Lisp came out in 1958 and ML in 1973, it seems to take decades for good ideas to catch on. For those cold decades, these languages were probably considered heretical or worse “not serious.”

I’m not saying Scalaz is going to be the next big thing. I don’t even know about it yet. But one thing for sure is that guys using it are serious about solving their problems. Or just as pedantic as the rest of the Scala community using pattern matching. Given that Haskell came out in 1990, the witch hunt may last a while, but I am going to keep an open mind.

Links 

• Older learning Scalaz based on Scalaz 7.0
• learning-scalaz.pdf

day 0 

I never set out to do a ”(you can) learn Scalaz in X days.” day 1 was written on Auguest 31, 2012 while Scalaz 7 was in milestone 7. Then day 2 was written the next day, and so on. It’s a web log of ”(me) learning Scalaz.” As such, it’s terse and minimal. Some of the days, I spent more time reading the book and trying code than writing the post.

Before we dive into the details, today I’m going to try a prequel to ease you in. Feel free to skip this part and come back later.

Intro to Scalaz 

There have been several Scalaz intros, but the best I’ve seen is Scalaz talk by Nick Partridge given at Melbourne Scala Users Group on March 22, 2010:

Scalaz talk is up - http://bit.ly/c2eTVR Lots of code showing how/why the library exists

— Nick Partridge (@nkpart) March 28, 2010

I’m going to borrow some material from it.

Scalaz consists of three parts:

1. New datatypes (Validation, NonEmptyList, etc)
2. Extensions to standard classes (OptionOps, ListOps, etc)
3. Implementation of every single general functions you need (ad-hoc polymorphism, traits + implicits)

What is polymorphism? 

Parametric polymorphism 

Nick says:

In this function head, it takes a list of A’s, and returns an A. And it doesn’t matter what the A is: It could be Ints, Strings, Oranges, Cars, whatever. Any A would work, and the function is defined for every A that there can be.

scala> def head[A](xs: List[A]): A = xs(0)
head: [A](xs: List[A])A

scala> head(1 :: 2 :: Nil)
res0: Int = 1

scala> case class Car(make: String)
defined class Car

scala> head(Car("Civic") :: Car("CR-V") :: Nil)
res1: Car = Car(Civic)

Haskell wiki says:

Parametric polymorphism refers to when the type of a value contains one or more (unconstrained) type variables, so that the value may adopt any type that results from substituting those variables with concrete types.

Subtype polymorphism 

Let’s think of a function plus that can add two values of type A:

scala> def plus[A](a1: A, a2: A): A = ???
plus: [A](a1: A, a2: A)A

Depending on the type A, we need to provide different definition for what it means to add them. One way to achieve this is through subtyping.

scala> trait Plus[A] {
         def plus(a2: A): A
       }
defined trait Plus

scala> def plus[A <: Plus[A]](a1: A, a2: A): A = a1.plus(a2)
plus: [A <: Plus[A]](a1: A, a2: A)A

We can at least provide different definitions of plus for A. But, this is not flexible since trait Plus needs to be mixed in at the time of defining the datatype. So it can’t work for Int and String.

Ad-hoc polymorphism 

The third approach in Scala is to provide an implicit conversion or implicit parameters for the trait.

scala> trait Plus[A] {
         def plus(a1: A, a2: A): A
       }
defined trait Plus

scala> def plus[A: Plus](a1: A, a2: A): A = implicitly[Plus[A]].plus(a1, a2)
plus: [A](a1: A, a2: A)(implicit evidence$1: Plus[A])A

This is truely ad-hoc in the sense that

1. we can provide separate function definitions for different types of A
2. we can provide function definitions to types (like Int) without access to its source code
3. the function definitions can be enabled or disabled in different scopes

The last point makes Scala’s ad-hoc polymorphism more powerful than that of Haskell. More on this topic can be found at Debasish Ghosh @debasishg’s Scala Implicits : Type Classes Here I Come.

Let’s look into plus function in more detail.

sum function 

Nick demonstrates an example of ad-hoc polymorphism by gradually making sum function more general, starting from a simple function that adds up a list of Ints:

scala> def sum(xs: List[Int]): Int = xs.foldLeft(0) { _ + _ }
sum: (xs: List[Int])Int

scala> sum(List(1, 2, 3, 4))
res3: Int = 10

Monoid 

If we try to generalize a little bit. I’m going to pull out a thing called Monoid. … It’s a type for which there exists a function mappend, which produces another type in the same set; and also a function that produces a zero.

scala> object IntMonoid {
         def mappend(a: Int, b: Int): Int = a + b
         def mzero: Int = 0
       }
defined module IntMonoid

If we pull that in, it sort of generalizes what’s going on here:

scala> def sum(xs: List[Int]): Int = xs.foldLeft(IntMonoid.mzero)(IntMonoid.mappend)
sum: (xs: List[Int])Int

scala> sum(List(1, 2, 3, 4))
res5: Int = 10

Now we’ll abstract on the type about Monoid, so we can define Monoid for any type A. So now IntMonoid is a monoid on Int:

scala> trait Monoid[A] {
         def mappend(a1: A, a2: A): A
         def mzero: A
       }
defined trait Monoid

scala> object IntMonoid extends Monoid[Int] {
         def mappend(a: Int, b: Int): Int = a + b
         def mzero: Int = 0
       }
defined module IntMonoid

What we can do is that sum take a List of Int and a monoid on Int to sum it:

scala> def sum(xs: List[Int], m: Monoid[Int]): Int = xs.foldLeft(m.mzero)(m.mappend)
sum: (xs: List[Int], m: Monoid[Int])Int

scala> sum(List(1, 2, 3, 4), IntMonoid)
res7: Int = 10

We are not using anything to do with Int here, so we can replace all Int with a general type:

scala> def sum[A](xs: List[A], m: Monoid[A]): A = xs.foldLeft(m.mzero)(m.mappend)
sum: [A](xs: List[A], m: Monoid[A])A

scala> sum(List(1, 2, 3, 4), IntMonoid)
res8: Int = 10

The final change we have to take is to make the Monoid implicit so we don’t have to specify it each time.

scala> def sum[A](xs: List[A])(implicit m: Monoid[A]): A = xs.foldLeft(m.mzero)(m.mappend)
sum: [A](xs: List[A])(implicit m: Monoid[A])A

scala> implicit val intMonoid = IntMonoid
intMonoid: IntMonoid.type = IntMonoid$@3387dfac

scala> sum(List(1, 2, 3, 4))
res9: Int = 10

Nick didn’t do this, but the implicit parameter is often written as a context bound:

scala> def sum[A: Monoid](xs: List[A]): A = {
         val m = implicitly[Monoid[A]]
         xs.foldLeft(m.mzero)(m.mappend)
       }
sum: [A](xs: List[A])(implicit evidence$1: Monoid[A])A

scala> sum(List(1, 2, 3, 4))
res10: Int = 10

Our sum function is pretty general now, appending any monoid in a list. We can test that by writing another Monoid for String. I’m also going to package these up in an object called Monoid. The reason for that is Scala’s implicit resolution rules: When it needs an implicit parameter of some type, it’ll look for anything in scope. It’ll include the companion object of the type that you’re looking for.

scala> :paste
// Entering paste mode (ctrl-D to finish)

trait Monoid[A] {
  def mappend(a1: A, a2: A): A
  def mzero: A
}
object Monoid {
  implicit val IntMonoid: Monoid[Int] = new Monoid[Int] {
    def mappend(a: Int, b: Int): Int = a + b
    def mzero: Int = 0
  }
  implicit val StringMonoid: Monoid[String] = new Monoid[String] {
    def mappend(a: String, b: String): String = a + b
    def mzero: String = ""
  }
}
def sum[A: Monoid](xs: List[A]): A = {
  val m = implicitly[Monoid[A]]
  xs.foldLeft(m.mzero)(m.mappend)
}

// Exiting paste mode, now interpreting.

defined trait Monoid
defined module Monoid
sum: [A](xs: List[A])(implicit evidence$1: Monoid[A])A

scala> sum(List("a", "b", "c"))
res12: String = abc

You can still provide different monoid directly to the function. We could provide an instance of monoid for Int using multiplications.

scala> val multiMonoid: Monoid[Int] = new Monoid[Int] {
         def mappend(a: Int, b: Int): Int = a * b
         def mzero: Int = 1
       }
multiMonoid: Monoid[Int] = $anon$1@48655fb6

scala> sum(List(1, 2, 3, 4))(multiMonoid)
res14: Int = 24

FoldLeft 

What we wanted was a function that generalized on List. … So we want to generalize on foldLeft operation.

scala> object FoldLeftList {
         def foldLeft[A, B](xs: List[A], b: B, f: (B, A) => B) = xs.foldLeft(b)(f)
       }
defined module FoldLeftList

scala> def sum[A: Monoid](xs: List[A]): A = {
         val m = implicitly[Monoid[A]]
         FoldLeftList.foldLeft(xs, m.mzero, m.mappend)
       }
sum: [A](xs: List[A])(implicit evidence$1: Monoid[A])A

scala> sum(List(1, 2, 3, 4))
res15: Int = 10

scala> sum(List("a", "b", "c"))
res16: String = abc

scala> sum(List(1, 2, 3, 4))(multiMonoid)
res17: Int = 24

Now we can apply the same abstraction to pull out FoldLeft typeclass.

scala> :paste
// Entering paste mode (ctrl-D to finish)

trait FoldLeft[F[_]] {
  def foldLeft[A, B](xs: F[A], b: B, f: (B, A) => B): B
}
object FoldLeft {
  implicit val FoldLeftList: FoldLeft[List] = new FoldLeft[List] {
    def foldLeft[A, B](xs: List[A], b: B, f: (B, A) => B) = xs.foldLeft(b)(f)
  }
}

def sum[M[_]: FoldLeft, A: Monoid](xs: M[A]): A = {
  val m = implicitly[Monoid[A]]
  val fl = implicitly[FoldLeft[M]]
  fl.foldLeft(xs, m.mzero, m.mappend)
}

// Exiting paste mode, now interpreting.

warning: there were 2 feature warnings; re-run with -feature for details
defined trait FoldLeft
defined module FoldLeft
sum: [M[_], A](xs: M[A])(implicit evidence$1: FoldLeft[M], implicit evidence$2: Monoid[A])A

scala> sum(List(1, 2, 3, 4))
res20: Int = 10

scala> sum(List("a", "b", "c"))
res21: String = abc

Both Int and List are now pulled out of sum.

Typeclasses in Scalaz 

In the above example, the traits Monoid and FoldLeft correspond to Haskell’s typeclass. Scalaz provides many typeclasses.

All this is broken down into just the pieces you need. So, it’s a bit like ultimate ducktyping because you define in your function definition that this is what you need and nothing more.

Method injection (enrich my library) 

If we were to write a function that sums two types using the Monoid, we need to call it like this.

scala> def plus[A: Monoid](a: A, b: A): A = implicitly[Monoid[A]].mappend(a, b)
plus: [A](a: A, b: A)(implicit evidence$1: Monoid[A])A

scala> plus(3, 4)
res25: Int = 7

We would like to provide an operator. But we don’t want to enrich just one type, but enrich all types that has an instance for Monoid. Let me do this in Scalaz 7 style.

scala> trait MonoidOp[A] {
         val F: Monoid[A]
         val value: A
         def |+|(a2: A) = F.mappend(value, a2)
       }
defined trait MonoidOp

scala> implicit def toMonoidOp[A: Monoid](a: A): MonoidOp[A] = new MonoidOp[A] {
         val F = implicitly[Monoid[A]]
         val value = a
       }
toMonoidOp: [A](a: A)(implicit evidence$1: Monoid[A])MonoidOp[A]

scala> 3 |+| 4
res26: Int = 7

scala> "a" |+| "b"
res28: String = ab

We were able to inject |+| to both Int and String with just one definition.

Standard type syntax 

Using the same technique, Scalaz also provides method injections for standard library types like Option and Boolean:

scala> 1.some | 2
res0: Int = 1

scala> Some(1).getOrElse(2)
res1: Int = 1

scala> (1 > 10)? 1 | 2
res3: Int = 2

scala> if (1 > 10) 1 else 2
res4: Int = 2

I hope you could get some feel on where Scalaz is coming from.

day 1 

typeclasses 101 

Learn You a Haskell for Great Good says:

A typeclass is a sort of interface that defines some behavior. If a type is a part of a typeclass, that means that it supports and implements the behavior the typeclass describes.

Scalaz says:

It provides purely functional data structures to complement those from the Scala standard library. It defines a set of foundational type classes (e.g. Functor, Monad) and corresponding instances for a large number of data structures.

Let’s see if I can learn Scalaz by learning me a Haskell.

sbt 

Here’s build.sbt to test Scalaz 7.1.0:

scalaVersion := "2.11.2"

val scalazVersion = "7.1.0"

libraryDependencies ++= Seq(
  "org.scalaz" %% "scalaz-core" % scalazVersion,
  "org.scalaz" %% "scalaz-effect" % scalazVersion,
  "org.scalaz" %% "scalaz-typelevel" % scalazVersion,
  "org.scalaz" %% "scalaz-scalacheck-binding" % scalazVersion % "test"
)

scalacOptions += "-feature"

initialCommands in console := "import scalaz._, Scalaz._"

All you have to do now is open the REPL using sbt 0.13.0:

$ sbt console
...
[info] downloading http://repo1.maven.org/maven2/org/scalaz/scalaz-core_2.10/7.0.5/scalaz-core_2.10-7.0.5.jar ...
import scalaz._
import Scalaz._
Welcome to Scala version 2.10.3 (Java HotSpot(TM) 64-Bit Server VM, Java 1.6.0_51).
Type in expressions to have them evaluated.
Type :help for more information.

scala>

There’s also API docs generated for Scalaz 7.1.0.

Equal 

LYAHFGG:

Eq is used for types that support equality testing. The functions its members implement are == and /=.

Scalaz equivalent for the Eq typeclass is called Equal:

scala> 1 === 1
res0: Boolean = true

scala> 1 === "foo"
<console>:14: error: could not find implicit value for parameter F0: scalaz.Equal[Object]
              1 === "foo"
              ^

scala> 1 == "foo"
<console>:14: warning: comparing values of types Int and String using `==' will always yield false
              1 == "foo"
                ^
res2: Boolean = false

scala> 1.some =/= 2.some
res3: Boolean = true

scala> 1 assert_=== 2
java.lang.RuntimeException: 1 ≠ 2

Instead of the standard ==, Equal enables ===, =/=, and assert_=== syntax by declaring equal method. The main difference is that === would fail compilation if you tried to compare Int and String.

Note: I originally had /== instead of =/=, but Eiríkr Åsheim pointed out to me:

@eed3si9n hey, was reading your scalaz tutorials. you should encourage people to use =/= and not /== since the latter has bad precedence.

— Eiríkr Åsheim (@d6) September 6, 2012

Normally comparison operators like != have lower higher precedence than &&, all letters, etc. Due to special precedence rule /== is recognized as an assignment operator because it ends with = and does not start with =, which drops to the bottom of the precedence:

scala> 1 != 2 && false
res4: Boolean = false

scala> 1 /== 2 && false
<console>:14: error: value && is not a member of Int
              1 /== 2 && false
                      ^

scala> 1 =/= 2 && false
res6: Boolean = false

Order 

LYAHFGG:

Ord is for types that have an ordering. Ord covers all the standard comparing functions such as >, <, >= and <=.

Scalaz equivalent for the Ord typeclass is Order:

scala> 1 > 2.0
res8: Boolean = false

scala> 1 gt 2.0
<console>:14: error: could not find implicit value for parameter F0: scalaz.Order[Any]
              1 gt 2.0
              ^

scala> 1.0 ?|? 2.0
res10: scalaz.Ordering = LT

scala> 1.0 max 2.0
res11: Double = 2.0

Order enables ?|? syntax which returns Ordering: LT, GT, and EQ. It also enables lt, gt, lte, gte, min, and max operators by declaring order method. Similar to Equal, comparing Int and Doubl fails compilation.

Show 

LYAHFGG:

Members of Show can be presented as strings.

Scalaz equivalent for the Show typeclass is Show:

scala> 3.show
res14: scalaz.Cord = 3

scala> 3.shows
res15: String = 3

scala> "hello".println
"hello"

Cord apparently is a purely functional data structure for potentially long Strings.

Read 

LYAHFGG:

Read is sort of the opposite typeclass of Show. The read function takes a string and returns a type which is a member of Read.

I could not find Scalaz equivalent for this typeclass.

Enum 

LYAHFGG:

Enum members are sequentially ordered types — they can be enumerated. The main advantage of the Enum typeclass is that we can use its types in list ranges. They also have defined successors and predecessors, which you can get with the succ and pred functions.

Scalaz equivalent for the Enum typeclass is Enum:

scala> 'a' to 'e'
res30: scala.collection.immutable.NumericRange.Inclusive[Char] = NumericRange(a, b, c, d, e)

scala> 'a' |-> 'e'
res31: List[Char] = List(a, b, c, d, e)

scala> 3 |=> 5
res32: scalaz.EphemeralStream[Int] = scalaz.EphemeralStreamFunctions$$anon$4@6a61c7b6

scala> 'B'.succ
res33: Char = C

Instead of the standard to, Enum enables |-> that returns a List by declaring pred and succ method on top of Order typeclass. There are a bunch of other operations it enables like -+-, ---, from, fromStep, pred, predx, succ, succx, |-->, |->, |==>, and |=>. It seems like these are all about stepping forward or backward, and returning ranges.

Bounded 

Bounded members have an upper and a lower bound.

Scalaz equivalent for Bounded seems to be Enum as well.

scala> implicitly[Enum[Char]].min
res43: Option[Char] = Some(?)

scala> implicitly[Enum[Char]].max
res44: Option[Char] = Some( )

scala> implicitly[Enum[Double]].max
res45: Option[Double] = Some(1.7976931348623157E308)

scala> implicitly[Enum[Int]].min
res46: Option[Int] = Some(-2147483648)

scala> implicitly[Enum[(Boolean, Int, Char)]].max
<console>:14: error: could not find implicit value for parameter e: scalaz.Enum[(Boolean, Int, Char)]
              implicitly[Enum[(Boolean, Int, Char)]].max
                        ^

Enum typeclass instance returns Option[T] for max values.

Num 

Num is a numeric typeclass. Its members have the property of being able to act like numbers.

I did not find Scalaz equivalent for Num, Floating, and Integral.

typeclasses 102 

I am now going to skip over to Chapter 8 Making Our Own Types and Typeclasses (Chapter 7 if you have the book) since the chapters in between are mostly about Haskell syntax.

A traffic light data type 

data TrafficLight = Red | Yellow | Green

In Scala this would be:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait TrafficLight
case object Red extends TrafficLight
case object Yellow extends TrafficLight
case object Green extends TrafficLight

Now let’s define an instance for Equal.

scala> implicit val TrafficLightEqual: Equal[TrafficLight] = Equal.equal(_ == _)
TrafficLightEqual: scalaz.Equal[TrafficLight] = scalaz.Equal$$anon$7@2457733b

Can I use it?

scala> Red === Yellow
<console>:18: error: could not find implicit value for parameter F0: scalaz.Equal[Product with Serializable with TrafficLight]
              Red === Yellow

So apparently Equal[TrafficLight] doesn’t get picked up because Equal has nonvariant subtyping: Equal[F]. If I turned TrafficLight to a case class then Red and Yellow would have the same type, but then I lose the tight pattern matching from sealed #fail.

scala> :paste
// Entering paste mode (ctrl-D to finish)

case class TrafficLight(name: String)
val red = TrafficLight("red")
val yellow = TrafficLight("yellow")
val green = TrafficLight("green")
implicit val TrafficLightEqual: Equal[TrafficLight] = Equal.equal(_ == _)
red === yellow

// Exiting paste mode, now interpreting.

defined class TrafficLight
red: TrafficLight = TrafficLight(red)
yellow: TrafficLight = TrafficLight(yellow)
green: TrafficLight = TrafficLight(green)
TrafficLightEqual: scalaz.Equal[TrafficLight] = scalaz.Equal$$anon$7@42988fee
res3: Boolean = false

a Yes-No typeclass 

Let’s see if we can make our own truthy value typeclass in the style of Scalaz. Except I am going to add my twist to it for the naming convention. Scalaz calls three or four different things using the name of the typeclass like Show, show, and show, which is a bit confusing.

I like to prefix the typeclass name with Can borrowing from CanBuildFrom, and name its method as verb + s, borrowing from sjson/sbinary. Since yesno doesn’t make much sense, let’s call ours truthy. Eventual goal is to get 1.truthy to return true. The downside is that the extra s gets appended if we want to use typeclass instances as functions like CanTruthy[Int].truthys(1).

scala> :paste
// Entering paste mode (ctrl-D to finish)

trait CanTruthy[A] { self =>
  /** @return true, if `a` is truthy. */
  def truthys(a: A): Boolean
}
object CanTruthy {
  def apply[A](implicit ev: CanTruthy[A]): CanTruthy[A] = ev
  def truthys[A](f: A => Boolean): CanTruthy[A] = new CanTruthy[A] {
    def truthys(a: A): Boolean = f(a)
  }
}
trait CanTruthyOps[A] {
  def self: A
  implicit def F: CanTruthy[A]
  final def truthy: Boolean = F.truthys(self)
}
object ToCanIsTruthyOps {
  implicit def toCanIsTruthyOps[A](v: A)(implicit ev: CanTruthy[A]) =
    new CanTruthyOps[A] {
      def self = v
      implicit def F: CanTruthy[A] = ev
    }
}

// Exiting paste mode, now interpreting.

defined trait CanTruthy
defined module CanTruthy
defined trait CanTruthyOps
defined module ToCanIsTruthyOps

scala> import ToCanIsTruthyOps._
import ToCanIsTruthyOps._

Here’s how we can define typeclass instances for Int:

scala> implicit val intCanTruthy: CanTruthy[Int] = CanTruthy.truthys({
         case 0 => false
         case _ => true
       })
intCanTruthy: CanTruthy[Int] = CanTruthy$$anon$1@71780051

scala> 10.truthy
res6: Boolean = true

Next is for List[A]:

scala> implicit def listCanTruthy[A]: CanTruthy[List[A]] = CanTruthy.truthys({
         case Nil => false
         case _   => true  
       })
listCanTruthy: [A]=> CanTruthy[List[A]]

scala> List("foo").truthy
res7: Boolean = true

scala> Nil.truthy
<console>:23: error: could not find implicit value for parameter ev: CanTruthy[scala.collection.immutable.Nil.type]
              Nil.truthy

It looks like we need to treat Nil specially because of the nonvariance.

scala> implicit val nilCanTruthy: CanTruthy[scala.collection.immutable.Nil.type] = CanTruthy.truthys(_ => false)
nilCanTruthy: CanTruthy[collection.immutable.Nil.type] = CanTruthy$$anon$1@1e5f0fd7

scala> Nil.truthy
res8: Boolean = false

And for Boolean using identity:

scala> implicit val booleanCanTruthy: CanTruthy[Boolean] = CanTruthy.truthys(identity)
booleanCanTruthy: CanTruthy[Boolean] = CanTruthy$$anon$1@334b4cb

scala> false.truthy
res11: Boolean = false

Using CanTruthy typeclass, let’s define truthyIf like LYAHFGG:

Now let’s make a function that mimics the if statement, but that works with YesNo values.

To delay the evaluation of the passed arguments, we can use pass-by-name:

scala> :paste
// Entering paste mode (ctrl-D to finish)

def truthyIf[A: CanTruthy, B, C](cond: A)(ifyes: => B)(ifno: => C) =
  if (cond.truthy) ifyes
  else ifno

// Exiting paste mode, now interpreting.

truthyIf: [A, B, C](cond: A)(ifyes: => B)(ifno: => C)(implicit evidence$1: CanTruthy[A])Any

Here’s how we can use it:

scala> truthyIf (Nil) {"YEAH!"} {"NO!"}
res12: Any = NO!

scala> truthyIf (2 :: 3 :: 4 :: Nil) {"YEAH!"} {"NO!"}
res13: Any = YEAH!

scala> truthyIf (true) {"YEAH!"} {"NO!"}
res14: Any = YEAH!

We’ll pick it from here later.

day 2 

Yesterday we reviewed a few basic typeclasses from Scalaz like Equal by using Learn You a Haskell for Great Good as the guide. We also created our own CanTruthy typeclass.

Functor 

LYAHFGG:

And now, we’re going to take a look at the Functor typeclass, which is basically for things that can be mapped over.

Like the book let’s look how it’s implemented:

trait Functor[F[_]]  { self =>
  /** Lift `f` into `F` and apply to `F[A]`. */
  def map[A, B](fa: F[A])(f: A => B): F[B]

  ...
}

Here are the injected operators it enables:

trait FunctorOps[F[_],A] extends Ops[F[A]] {
  implicit def F: Functor[F]
  ////
  import Leibniz.===

  final def map[B](f: A => B): F[B] = F.map(self)(f)

  ...
}

So this defines map method, which accepts a function A => B and returns F[B]. We are quite familiar with map method for collections:

scala> List(1, 2, 3) map {_ + 1}
res15: List[Int] = List(2, 3, 4)

Scalaz defines Functor instances for Tuples.

scala> (1, 2, 3) map {_ + 1}
res28: (Int, Int, Int) = (1,2,4)

Note that the operation is only applied to the last value in the Tuple, (see scalaz group discussion).

Function as Functors 

Scalaz also defines Functor instance for Function1.

scala> ((x: Int) => x + 1) map {_ * 7}
res30: Int => Int = <function1>

scala> res30(3)
res31: Int = 28

This is interesting. Basically map gives us a way to compose functions, except the order is in reverse from f compose g. No wonder Scalaz provides ∘ as an alias of map. Another way of looking at Function1 is that it’s an infinite map from the domain to the range. Now let’s skip the input and output stuff and go to Functors, Applicative Functors and Monoids.

How are functions functors? …

What does the type fmap :: (a -> b) -> (r -> a) -> (r -> b) for this instance tell us? Well, we see that it takes a function from a to b and a function from r to a and returns a function from r to b. Does this remind you of anything? Yes! Function composition!

Oh man, LYAHFGG came to the same conclusion as I did about the function composition. But wait..

ghci> fmap (*3) (+100) 1
303
ghci> (*3) . (+100) $ 1  
303

In Haskell, the fmap seems to be working as the same order as f compose g. Let’s check in Scala using the same numbers:

scala> (((_: Int) * 3) map {_ + 100}) (1)
res40: Int = 103

Something is not right. Let’s compare the declaration of fmap and Scalaz’s map operator:

fmap :: (a -> b) -> f a -> f b

and here’s Scalaz:

final def map[B](f: A => B): F[B] = F.map(self)(f)

So the order is completely different. Since map here’s an injected method of F[A], the data structure to be mapped over comes first, then the function comes next. Let’s see List:

ghci> fmap (*3) [1, 2, 3]
[3,6,9]

and

scala> List(1, 2, 3) map {3*}
res41: List[Int] = List(3, 6, 9)

The order is reversed here too.

[We can think of fmap as] a function that takes a function and returns a new function that’s just like the old one, only it takes a functor as a parameter and returns a functor as the result. It takes an a -> b function and returns a function f a -> f b. This is called lifting a function.

ghci> :t fmap (*2)  
fmap (*2) :: (Num a, Functor f) => f a -> f a  
ghci> :t fmap (replicate 3)  
fmap (replicate 3) :: (Functor f) => f a -> f [a]  

Are we going to miss out on this lifting goodness? There are several neat functions under Functor typeclass. One of them is called lift:

scala> Functor[List].lift {(_: Int) * 2}
res45: List[Int] => List[Int] = <function1>

scala> res45(List(3))
res47: List[Int] = List(6)

Functor also enables some operators that overrides the values in the data structure like >|, as, fpair, strengthL, strengthR, and void:

scala> List(1, 2, 3) >| "x"
res47: List[String] = List(x, x, x)

scala> List(1, 2, 3) as "x"
res48: List[String] = List(x, x, x)

scala> List(1, 2, 3).fpair
res49: List[(Int, Int)] = List((1,1), (2,2), (3,3))

scala> List(1, 2, 3).strengthL("x")
res50: List[(String, Int)] = List((x,1), (x,2), (x,3))

scala> List(1, 2, 3).strengthR("x")
res51: List[(Int, String)] = List((1,x), (2,x), (3,x))

scala> List(1, 2, 3).void
res52: List[Unit] = List((), (), ())

Applicative 

LYAHFGG:

So far, when we were mapping functions over functors, we usually mapped functions that take only one parameter. But what happens when we map a function like *, which takes two parameters, over a functor?

scala> List(1, 2, 3, 4) map {(_: Int) * (_:Int)}
<console>:14: error: type mismatch;
 found   : (Int, Int) => Int
 required: Int => ?
              List(1, 2, 3, 4) map {(_: Int) * (_:Int)}
                                             ^

Oops. We have to curry this:

scala> List(1, 2, 3, 4) map {(_: Int) * (_:Int)}.curried
res11: List[Int => Int] = List(<function1>, <function1>, <function1>, <function1>)

scala> res11 map {_(9)}
res12: List[Int] = List(9, 18, 27, 36)

LYAHFGG:

Meet the Applicative typeclass. It lies in the Control.Applicative module and it defines two methods, pure and <*>.

Let’s see the contract for Scalaz’s Applicative:

trait Applicative[F[_]] extends Apply[F] { self =>
  def point[A](a: => A): F[A]

  /** alias for `point` */
  def pure[A](a: => A): F[A] = point(a)

  ...
}

So Applicative extends another typeclass Apply, and introduces point and its alias pure.

LYAHFGG:

pure should take a value of any type and return an applicative value with that value inside it. … A better way of thinking about pure would be to say that it takes a value and puts it in some sort of default (or pure) context—a minimal context that still yields that value.

Scalaz likes the name point instead of pure, and it seems like it’s basically a constructor that takes value A and returns F[A]. It doesn’t introduce an operator, but it introduces point method and its symbolic alias η to all data types.

scala> 1.point[List]
res14: List[Int] = List(1)

scala> 1.point[Option]
res15: Option[Int] = Some(1)

scala> 1.point[Option] map {_ + 2}
res16: Option[Int] = Some(3)

scala> 1.point[List] map {_ + 2}
res17: List[Int] = List(3)

I can’t really express it in words yet, but there’s something cool about the fact that constructor is abstracted out.

Apply 

LYAHFGG:

You can think of <*> as a sort of a beefed-up fmap. Whereas fmap takes a function and a functor and applies the function inside the functor value, <*> takes a functor that has a function in it and another functor and extracts that function from the first functor and then maps it over the second one.

trait Apply[F[_]] extends Functor[F] { self =>
  def ap[A,B](fa: => F[A])(f: => F[A => B]): F[B]
}

Using ap, Apply enables <*>, *>, and <* operator.

scala>  9.some <*> {(_: Int) + 3}.some
res20: Option[Int] = Some(12)

As expected.

*> and <* are variations that returns only the rhs or lhs.

scala> 1.some <* 2.some
res35: Option[Int] = Some(1)

scala> none <* 2.some
res36: Option[Nothing] = None

scala> 1.some *> 2.some
res38: Option[Int] = Some(2)

scala> none *> 2.some
res39: Option[Int] = None

Option as Apply 

We can use <*>:

scala> 9.some <*> {(_: Int) + 3}.some
res57: Option[Int] = Some(12)

scala> 3.some <*> { 9.some <*> {(_: Int) + (_: Int)}.curried.some }
res58: Option[Int] = Some(12)

Applicative Style 

Another thing I found in 7.0.0-M3 is a new notation that extracts values from containers and apply them to a single function:

scala> ^(3.some, 5.some) {_ + _}
res59: Option[Int] = Some(8)

scala> ^(3.some, none[Int]) {_ + _}
res60: Option[Int] = None

This is actually useful because for one-function case, we no longer need to put it into the container. I am guessing that this is why Scalaz 7 does not introduce any operator from Applicative itself. Whatever the case, it seems like we no longer need Pointed or <$>.

The new ^(f1, f2) {...} style is not without the problem though. It doesn’t seem to handle Applicatives that takes two type parameters like Function1, Writer, and Validation. There’s another way called Applicative Builder, which apparently was the way it worked in Scalaz 6, got deprecated in M3, but will be vindicated again because of ^(f1, f2) {...}’s issues.

Here’s how it looks:

scala> (3.some |@| 5.some) {_ + _}
res18: Option[Int] = Some(8)

We will use |@| style for now.

Lists as Apply 

LYAHFGG:

Lists (actually the list type constructor, []) are applicative functors. What a surprise!

Let’s see if we can use <*> and |@|:

scala> List(1, 2, 3) <*> List((_: Int) * 0, (_: Int) + 100, (x: Int) => x * x)
res61: List[Int] = List(0, 0, 0, 101, 102, 103, 1, 4, 9)

scala> List(3, 4) <*> { List(1, 2) <*> List({(_: Int) + (_: Int)}.curried, {(_: Int) * (_: Int)}.curried) }
res62: List[Int] = List(4, 5, 5, 6, 3, 4, 6, 8)

scala> (List("ha", "heh", "hmm") |@| List("?", "!", ".")) {_ + _}
res63: List[String] = List(ha?, ha!, ha., heh?, heh!, heh., hmm?, hmm!, hmm.)

Zip Lists 

LYAHFGG:

However, [(+3),(*2)] <*> [1,2] could also work in such a way that the first function in the left list gets applied to the first value in the right one, the second function gets applied to the second value, and so on. That would result in a list with two values, namely [4,4]. You could look at it as [1 + 3, 2 * 2].

This can be done in Scalaz, but not easily.

scala> streamZipApplicative.ap(Tags.Zip(Stream(1, 2))) (Tags.Zip(Stream({(_: Int) + 3}, {(_: Int) * 2})))
res32: scala.collection.immutable.Stream[Int] with Object{type Tag = scalaz.Tags.Zip} = Stream(4, ?)

scala> res32.toList
res33: List[Int] = List(4, 4)

We’ll see more examples of tagged type tomorrow.

Useful functions for Applicatives 

LYAHFGG:

Control.Applicative defines a function that’s called liftA2, which has a type of

liftA2 :: (Applicative f) => (a -> b -> c) -> f a -> f b -> f c .

There’s Apply[F].lift2:

scala> Apply[Option].lift2((_: Int) :: (_: List[Int]))
res66: (Option[Int], Option[List[Int]]) => Option[List[Int]] = <function2>

scala> res66(3.some, List(4).some)
res67: Option[List[Int]] = Some(List(3, 4))

LYAHFGG:

Let’s try implementing a function that takes a list of applicatives and returns an applicative that has a list as its result value. We’ll call it sequenceA.

sequenceA :: (Applicative f) => [f a] -> f [a]  
sequenceA [] = pure []  
sequenceA (x:xs) = (:) <$> x <*> sequenceA xs  

Let’s try implementing this in Scalaz!

scala> def sequenceA[F[_]: Applicative, A](list: List[F[A]]): F[List[A]] = list match {
         case Nil     => (Nil: List[A]).point[F]
         case x :: xs => (x |@| sequenceA(xs)) {_ :: _} 
       }
sequenceA: [F[_], A](list: List[F[A]])(implicit evidence$1: scalaz.Applicative[F])F[List[A]]

Let’s test it:

scala> sequenceA(List(1.some, 2.some))
res82: Option[List[Int]] = Some(List(1, 2))

scala> sequenceA(List(3.some, none, 1.some))
res85: Option[List[Int]] = None

scala> sequenceA(List(List(1, 2, 3), List(4, 5, 6)))
res86: List[List[Int]] = List(List(1, 4), List(1, 5), List(1, 6), List(2, 4), List(2, 5), List(2, 6), List(3, 4), List(3, 5), List(3, 6))

We got the right answers. What’s interesting here is that we did end up needing Pointed after all, and sequenceA is generic in typeclassy way.

For Function1 with Int fixed example, we have to unfortunately invoke a dark magic.

scala> type Function1Int[A] = ({type l[A]=Function1[Int, A]})#l[A]
defined type alias Function1Int

scala> sequenceA(List((_: Int) + 3, (_: Int) + 2, (_: Int) + 1): List[Function1Int[Int]])
res1: Int => List[Int] = <function1>

scala> res1(3)
res2: List[Int] = List(6, 5, 4)

It took us a while, but I am glad we got this far. We’ll pick it up from here later.

day 3 

Yesterday we started with Functor, which adds map operator, and ended with polymorphic sequenceA function that uses Pointed[F].point and Applicative ^(f1, f2) {_ :: _} syntax.

Kinds and some type-foo 

One section I should’ve covered yesterday from Making Our Own Types and Typeclasses but didn’t is about kinds and types. I thought it wouldn’t matter much to understand Scalaz, but it does, so we need to have the talk.

Learn You a Haskell For Great Good says:

Types are little labels that values carry so that we can reason about the values. But types have their own little labels, called kinds. A kind is more or less the type of a type. … What are kinds and what are they good for? Well, let’s examine the kind of a type by using the :k command in GHCI.

I did not find :k command for Scala REPL in Scala 2.10, so I wrote one: kind.scala. With George Leontiev (@folone), who sent in scala/scala#2340, and others’ help :kind command is now part of Scala 2.11. Let’s try using it:

scala> :k Int
scala.Int's kind is A

scala> :k -v Int
scala.Int's kind is A
*
This is a proper type.

scala> :k -v Option
scala.Option's kind is F[+A]
* -(+)-> *
This is a type constructor: a 1st-order-kinded type.

scala> :k -v Either
scala.util.Either's kind is F[+A1,+A2]
* -(+)-> * -(+)-> *
This is a type constructor: a 1st-order-kinded type.

scala> :k -v Equal
scalaz.Equal's kind is F[A]
* -> *
This is a type constructor: a 1st-order-kinded type.

scala> :k -v Functor
scalaz.Functor's kind is X[F[A]]
(* -> *) -> *
This is a type constructor that takes type constructor(s): a higher-kinded type.

From the top. Int and every other types that you can make a value out of is called a proper type and denoted with a symbol * (read “type”). This is analogous to value 1 at value-level. Using Scala’s type variable notation this could be written as A.

A first-order value, or a value constructor like (_: Int) + 3, is normally called a function. Similarly, a first-order-kinded type is a type that accepts other types to create a proper type. This is normally called a type constructor. Option, Either, and Equal are all first-order-kinded. To denote that these accept other types, we use curried notation like * -> * and * -> * -> *. Note, Option[Int] is *; Option is * -> *. Using Scala’s type variable notation they could be written as F[+A] and F[+A1,+A2].

A higher-order value like (f: Int => Int, list: List[Int]) => list map {f}, a function that accepts other functions is normally called higher-order function. Similarly, a higher-kinded type is a type constructor that accepts other type constructors. It probably should be called a higher-kinded type constructor but the name is not used. These are denoted as (* -> *) -> *. Using Scala’s type variable notation this could be written as X[F[A]].

In case of Scalaz 7.1, Equal and others have the kind F[A] while Functor and all its derivatives have the kind X[F[A]]. Scala encodes (or complects) the notion of type class using type constructor, and the terminology tend get jumbled up. For example, the data structure List forms a functor, in the sense that an instance Functor[List] can be derived for List. Since there should be only one instance for List, we can say that List is a functor. See the following discussion for more on “is-a”:

In FP, "is-a" means "an instance can be derived from." @jimduey #CPL14 It's a provable relationship, not reliant on LSP.

— Jessica Kerr (@jessitron) February 25, 2014

Since List is F[+A], it’s easy to remember that F relates to a functor. Except, the typeclass definition Functor needs to wrap F[A] around, so its kind is X[F[A]]. To add to the confusion, the fact that Scala can treat type constructor as a first class variable was novel enough, that the compiler calls first-order kinded type as “higher-kinded type”:

scala> trait Test {
         type F[_]
       }
<console>:14: warning: higher-kinded type should be enabled
by making the implicit value scala.language.higherKinds visible.
This can be achieved by adding the import clause 'import scala.language.higherKinds'
or by setting the compiler option -language:higherKinds.
See the Scala docs for value scala.language.higherKinds for a discussion
why the feature should be explicitly enabled.
         type F[_]
              ^

You normally don’t have to worry about this if you are using injected operators like:

scala> List(1, 2, 3).shows
res11: String = [1,2,3]

But if you want to use Show[A].shows, you have to know it’s Show[List[Int]], not Show[List]. Similarly, if you want to lift a function, you need to know that it’s Functor[F] (F is for Functor):

scala> Functor[List[Int]].lift((_: Int) + 2)
<console>:14: error: List[Int] takes no type parameters, expected: one
              Functor[List[Int]].lift((_: Int) + 2)
                      ^

scala> Functor[List].lift((_: Int) + 2)
res13: List[Int] => List[Int] = <function1>

In the cheat sheet I started I originally had type parameters for Equal written as Equal[F], which is the same as Scalaz 7’s source code. Adam Rosien pointed out to me that it should be Equal[A].

@eed3si9n love the scalaz cheat sheet start, but using the type param F usually means Functor, what about A instead?

— Adam Rosien (@arosien) September 1, 2012

Now it makes sense why!

Tagged type 

If you have the book Learn You a Haskell for Great Good you get to start a new chapter: Monoids. For the website, it’s still Functors, Applicative Functors and Monoids.

LYAHFGG:

The newtype keyword in Haskell is made exactly for these cases when we want to just take one type and wrap it in something to present it as another type.

This is a language-level feature in Haskell, so one would think we can’t port it over to Scala. About an year ago (September 2011) Miles Sabin (@milessabin) wrote a gist and called it Tagged and Jason Zaugg (@retronym) added @@ type alias.

type Tagged[U] = { type Tag = U }
type @@[T, U] = T with Tagged[U]

Eric Torreborre (@etorreborre) wrote Practical uses for Unboxed Tagged Types and Tim Perrett wrote Unboxed new types within Scalaz7 if you want to read up on it.

Suppose we want a way to express mass using kilogram, because kg is the international standard of unit. Normally we would pass in Double and call it a day, but we can’t distinguish that from other Double values. Can we use case class for this?

case class KiloGram(value: Double)

Although it does adds type safety, it’s not fun to use because we have to call x.value every time we need to extract the value out of it. Tagged type to the rescue.

scala> sealed trait KiloGram
defined trait KiloGram

scala> def KiloGram[A](a: A): A @@ KiloGram = Tag[A, KiloGram](a)
KiloGram: [A](a: A)scalaz.@@[A,KiloGram]

scala> val mass = KiloGram(20.0)
mass: scalaz.@@[Double,KiloGram] = 20.0

scala> 2 * Tag.unwrap(mass) // this doesn't work on REPL
res2: Double = 40.0

scala> 2 * Tag.unwrap(mass)
<console>:17: error: wrong number of type parameters for method unwrap$mDc$sp: [T](a: Object{type Tag = T; type Self = Double})Double
              2 * Tag.unwrap(mass)
                      ^

scala> 2 * scalaz.Tag.unsubst[Double, Id, KiloGram](mass)
res2: Double = 40.0

Note: As of scalaz 7.1 we need to explicitly unwrap tags. Previously we could just do 2 * mass. Due to a problem on REPL SI-8871, Tag.unwrap doesn’t work, so I had to use Tag.unsubst. Just to be clear, A @@ KiloGram is an infix notation of scalaz.@@[A, KiloGram]. We can now define a function that calculates relativistic energy.

scala> sealed trait JoulePerKiloGram
defined trait JoulePerKiloGram

scala> def JoulePerKiloGram[A](a: A): A @@ JoulePerKiloGram = Tag[A, JoulePerKiloGram](a)
JoulePerKiloGram: [A](a: A)scalaz.@@[A,JoulePerKiloGram]

scala> def energyR(m: Double @@ KiloGram): Double @@ JoulePerKiloGram =
         JoulePerKiloGram(299792458.0 * 299792458.0 * Tag.unsubst[Double, Id, KiloGram](m))
energyR: (m: scalaz.@@[Double,KiloGram])scalaz.@@[Double,JoulePerKiloGram]

scala> energyR(mass)
res4: scalaz.@@[Double,JoulePerKiloGram] = 1.79751035747363533E18

scala> energyR(10.0)
<console>:18: error: type mismatch;
 found   : Double(10.0)
 required: scalaz.@@[Double,KiloGram]
    (which expands to)  AnyRef{type Tag = KiloGram; type Self = Double}
              energyR(10.0)
                      ^

As you can see, passing in plain Double to energyR fails at compile-time. This sounds exactly like newtype except it’s even better because we can define Int @@ KiloGram if we want.

About those Monoids 

LYAHFGG:

It seems that both * together with 1 and ++ along with [] share some common properties: - The function takes two parameters. - The parameters and the returned value have the same type. - There exists such a value that doesn’t change other values when used with the binary function.

Let’s check it out in Scala:

scala> 4 * 1
res16: Int = 4

scala> 1 * 9
res17: Int = 9

scala> List(1, 2, 3) ++ Nil
res18: List[Int] = List(1, 2, 3)

scala> Nil ++ List(0.5, 2.5)
res19: List[Double] = List(0.5, 2.5)

Looks right.

LYAHFGG:

It doesn’t matter if we do (3 * 4) * 5 or 3 * (4 * 5). Either way, the result is 60. The same goes for ++. … We call this property associativity. * is associative, and so is ++, but -, for example, is not.

Let’s check this too:

scala> (3 * 2) * (8 * 5) assert_=== 3 * (2 * (8 * 5))

scala> List("la") ++ (List("di") ++ List("da")) assert_=== (List("la") ++ List("di")) ++ List("da")

No error means, they are equal. Apparently this is what monoid is.

Monoid 

LYAHFGG:

A monoid is when you have an associative binary function and a value which acts as an identity with respect to that function.

Let’s see the typeclass contract for Monoid in Scalaz:

trait Monoid[A] extends Semigroup[A] { self =>
  ////
  /** The identity element for `append`. */
  def zero: A

  ...
}

Semigroup 

Looks like Monoid extends Semigroup so let’s look at its typeclass.

trait Semigroup[A]  { self =>
  def append(a1: A, a2: => A): A
  ...
}

Here are the operators:

trait SemigroupOps[A] extends Ops[A] {
  final def |+|(other: => A): A = A.append(self, other)
  final def mappend(other: => A): A = A.append(self, other)
  final def ⊹(other: => A): A = A.append(self, other)
}

It introduces mappend operator with symbolic alias |+| and ⊹.

LYAHFGG:

We have mappend, which, as you’ve probably guessed, is the binary function. It takes two values of the same type and returns a value of that type as well.

LYAHFGG also warns that just because it’s named mappend it does not mean it’s appending something, like in the case of *. Let’s try using this.

scala> List(1, 2, 3) mappend List(4, 5, 6)
res23: List[Int] = List(1, 2, 3, 4, 5, 6)

scala> "one" mappend "two"
res25: String = onetwo

I think the idiomatic Scalaz way is to use |+|:

scala> List(1, 2, 3) |+| List(4, 5, 6)
res26: List[Int] = List(1, 2, 3, 4, 5, 6)

scala> "one" |+| "two"
res27: String = onetwo

This looks more concise.

Back to Monoid 

trait Monoid[A] extends Semigroup[A] { self =>
  ////
  /** The identity element for `append`. */
  def zero: A

  ...
}

LYAHFGG:

mempty represents the identity value for a particular monoid.

Scalaz calls this zero instead.

scala> Monoid[List[Int]].zero
res15: List[Int] = List()

scala> Monoid[String].zero
res16: String = ""

Tags.Multiplication 

LYAHFGG:

So now that there are two equally valid ways for numbers (addition and multiplication) to be monoids, which way do choose? Well, we don’t have to.

This is where Scalaz 7.1 uses tagged type. The built-in tags are Tags. There are 8 tags for Monoids and 1 named Zip for Applicative. (Is this the Zip List I couldn’t find yesterday?)

scala> Tags.Multiplication(10) |+| Monoid[Int @@ Tags.Multiplication].zero
res21: scalaz.@@[Int,scalaz.Tags.Multiplication] = 10

Nice! So we can multiply numbers using |+|. For addition, we use plain Int.

scala> 10 |+| Monoid[Int].zero
res22: Int = 10

Tags.Disjunction and Tags.Conjunction 

LYAHFGG:

Another type which can act like a monoid in two distinct but equally valid ways is Bool. The first way is to have the or function || act as the binary function along with False as the identity value. … The other way for Bool to be an instance of Monoid is to kind of do the opposite: have && be the binary function and then make True the identity value.

In Scalaz 7 these are called Boolean @@ Tags.Disjunction and Boolean @@ Tags.Conjunction respectively.

scala> Tags.Disjunction(true) |+| Tags.Disjunction(false)
res28: scalaz.@@[Boolean,scalaz.Tags.Disjunction] = true

scala> Monoid[Boolean @@ Tags.Disjunction].zero |+| Tags.Disjunction(true)
res29: scalaz.@@[Boolean,scalaz.Tags.Disjunction] = true

scala> Monoid[Boolean @@ Tags.Disjunction].zero |+| Monoid[Boolean @@ Tags.Disjunction].zero
res30: scalaz.@@[Boolean,scalaz.Tags.Disjunction] = false

scala> Monoid[Boolean @@ Tags.Conjunction].zero |+| Tags.Conjunction(true)
res31: scalaz.@@[Boolean,scalaz.Tags.Conjunction] = true

scala> Monoid[Boolean @@ Tags.Conjunction].zero |+| Tags.Conjunction(false)
res32: scalaz.@@[Boolean,scalaz.Tags.Conjunction] = false

Ordering as Monoid 

LYAHFGG:

With Ordering, we have to look a bit harder to recognize a monoid, but it turns out that its Monoid instance is just as intuitive as the ones we’ve met so far and also quite useful.

Sounds odd, but let’s check it out.

scala> Ordering.LT |+| Ordering.GT
<console>:14: error: value |+| is not a member of object scalaz.Ordering.LT
              Ordering.LT |+| Ordering.GT
                          ^

scala> (Ordering.LT: Ordering) |+| (Ordering.GT: Ordering)
res42: scalaz.Ordering = LT

scala> (Ordering.GT: Ordering) |+| (Ordering.LT: Ordering)
res43: scalaz.Ordering = GT

scala> Monoid[Ordering].zero |+| (Ordering.LT: Ordering)
res44: scalaz.Ordering = LT

scala> Monoid[Ordering].zero |+| (Ordering.GT: Ordering)
res45: scalaz.Ordering = GT

LYAHFGG:

OK, so how is this monoid useful? Let’s say you were writing a function that takes two strings, compares their lengths, and returns an Ordering. But if the strings are of the same length, then instead of returning EQ right away, we want to compare them alphabetically.

Because the left comparison is kept unless it’s Ordering.EQ we can use this to compose two levels of comparisons. Let’s try implementing lengthCompare using Scalaz:

scala> def lengthCompare(lhs: String, rhs: String): Ordering =
         (lhs.length ?|? rhs.length) |+| (lhs ?|? rhs)
lengthCompare: (lhs: String, rhs: String)scalaz.Ordering

scala> lengthCompare("zen", "ants")
res46: scalaz.Ordering = LT

scala> lengthCompare("zen", "ant")
res47: scalaz.Ordering = GT

It works. “zen” is LT compared to “ants” because it’s shorter.

We still have more Monoids, but let’s call it a day. We’ll pick it up from here later.

day 4 

Yesterday we reviewed kinds and types, explored Tagged type, and started looking at Semigroup and Monoid as a way of abstracting binary operations over various types.

Also a comment from Jason Zaugg:

This might be a good point to pause and discuss the laws by which a well behaved type class instance must abide.

I’ve been skipping all the sections in Learn You a Haskell for Great Good about the laws and we got pulled over.

Functor Laws 

LYAHFGG:

All functors are expected to exhibit certain kinds of functor-like properties and behaviors. … The first functor law states that if we map the id function over a functor, the functor that we get back should be the same as the original functor.

In other words,

scala> List(1, 2, 3) map {identity} assert_=== List(1, 2, 3)

The second law says that composing two functions and then mapping the resulting function over a functor should be the same as first mapping one function over the functor and then mapping the other one.

In other words,

scala> (List(1, 2, 3) map {{(_: Int) * 3} map {(_: Int) + 1}}) assert_=== (List(1, 2, 3) map {(_: Int) * 3} map {(_: Int) + 1})

These are laws the implementer of the functors must abide, and not something the compiler can check for you. Scalaz 7+ ships with FunctorLaw traits that describes this in code:

trait FunctorLaw {
  /** The identity function, lifted, is a no-op. */
  def identity[A](fa: F[A])(implicit FA: Equal[F[A]]): Boolean = FA.equal(map(fa)(x => x), fa)

  /**
   * A series of maps may be freely rewritten as a single map on a
   * composed function.
   */
  def associative[A, B, C](fa: F[A], f1: A => B, f2: B => C)(implicit FC: Equal[F[C]]): Boolean = FC.equal(map(map(fa)(f1))(f2), map(fa)(f2 compose f1))
}

Not only that, it ships with ScalaCheck bindings to test these properties using arbitrary values. Here’s the build.sbt to check from REPL:

scalaVersion := "2.11.2"

val scalazVersion = "7.1.0"

libraryDependencies ++= Seq(
  "org.scalaz" %% "scalaz-core" % scalazVersion,
  "org.scalaz" %% "scalaz-effect" % scalazVersion,
  "org.scalaz" %% "scalaz-typelevel" % scalazVersion,
  "org.scalaz" %% "scalaz-scalacheck-binding" % scalazVersion % "test"
)

scalacOptions += "-feature"

initialCommands in console := "import scalaz._, Scalaz._"

initialCommands in console in Test := "import scalaz._, Scalaz._, scalacheck.ScalazProperties._, scalacheck.ScalazArbitrary._,scalacheck.ScalaCheckBinding._"

Instead of the usual sbt console, run sbt test:console:

$ sbt test:console
[info] Starting scala interpreter...
[info]
import scalaz._
import Scalaz._
import scalacheck.ScalazProperties._
import scalacheck.ScalazArbitrary._
import scalacheck.ScalaCheckBinding._
Welcome to Scala version 2.10.3 (Java HotSpot(TM) 64-Bit Server VM, Java 1.6.0_45).
Type in expressions to have them evaluated.
Type :help for more information.

scala>

Here’s how you test if List meets the functor laws:

scala> functor.laws[List].check
+ functor.identity: OK, passed 100 tests.
+ functor.associative: OK, passed 100 tests.

Breaking the law 

Following the book, let’s try breaking the law.

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait COption[+A] {}
case class CSome[A](counter: Int, a: A) extends COption[A]
case object CNone extends COption[Nothing]

implicit def coptionEqual[A]: Equal[COption[A]] = Equal.equalA
implicit val coptionFunctor = new Functor[COption] {
  def map[A, B](fa: COption[A])(f: A => B): COption[B] = fa match {
    case CNone => CNone
    case CSome(c, a) => CSome(c + 1, f(a))
  }
}

// Exiting paste mode, now interpreting.

defined trait COption
defined class CSome
defined module CNone
coptionEqual: [A]=> scalaz.Equal[COption[A]]
coptionFunctor: scalaz.Functor[COption] = $anon$1@42538425

scala> (CSome(0, "ho"): COption[String]) map {(_: String) + "ha"}
res4: COption[String] = CSome(1,hoha)

scala> (CSome(0, "ho"): COption[String]) map {identity}
res5: COption[String] = CSome(1,ho)

It’s breaking the first law. Let’s see if we can catch this.

scala> functor.laws[COption].check
<console>:26: error: could not find implicit value for parameter af: org.scalacheck.Arbitrary[COption[Int]]
              functor.laws[COption].check
                          ^

So now we have to supply “arbitrary” COption[A] implicitly:

scala> import org.scalacheck.{Gen, Arbitrary}
import org.scalacheck.{Gen, Arbitrary}

scala> implicit def COptionArbiterary[A](implicit a: Arbitrary[A]): Arbitrary[COption[A]] =
         a map { a => (CSome(0, a): COption[A]) }
COptionArbiterary: [A](implicit a: org.scalacheck.Arbitrary[A])org.scalacheck.Arbitrary[COption[A]]

This is pretty cool. ScalaCheck on its own does not ship map method, but Scalaz injected it as a Functor[Arbitrary]! Not much of an arbitrary COption, but I don’t know enough ScalaCheck, so this will have to do.

scala> functor.laws[COption].check
! functor.identity: Falsified after 0 passed tests.
> ARG_0: CSome(0,-170856004)
! functor.associative: Falsified after 0 passed tests.
> ARG_0: CSome(0,1)
> ARG_1: <function1>
> ARG_2: <function1>

And the test fails as expected.

Applicative Laws 

Here are the laws for Applicative:

  trait ApplicativeLaw extends FunctorLaw {
    def identityAp[A](fa: F[A])(implicit FA: Equal[F[A]]): Boolean =
      FA.equal(ap(fa)(point((a: A) => a)), fa)

    def composition[A, B, C](fbc: F[B => C], fab: F[A => B], fa: F[A])(implicit FC: Equal[F[C]]) =
      FC.equal(ap(ap(fa)(fab))(fbc), ap(fa)(ap(fab)(ap(fbc)(point((bc: B => C) => (ab: A => B) => bc compose ab)))))

    def homomorphism[A, B](ab: A => B, a: A)(implicit FB: Equal[F[B]]): Boolean =
      FB.equal(ap(point(a))(point(ab)), point(ab(a)))

    def interchange[A, B](f: F[A => B], a: A)(implicit FB: Equal[F[B]]): Boolean =
      FB.equal(ap(point(a))(f), ap(f)(point((f: A => B) => f(a))))
  }

LYAHFGG is skipping the details on this, so I am skipping too.

Semigroup Laws 

Here are the Semigroup Laws:

  /**
   * A semigroup in type F must satisfy two laws:
    *
    *  - '''closure''': `∀ a, b in F, append(a, b)` is also in `F`. This is enforced by the type system.
    *  - '''associativity''': `∀ a, b, c` in `F`, the equation `append(append(a, b), c) = append(a, append(b , c))` holds.
   */
  trait SemigroupLaw {
    def associative(f1: F, f2: F, f3: F)(implicit F: Equal[F]): Boolean =
      F.equal(append(f1, append(f2, f3)), append(append(f1, f2), f3))
  }

Remember, 1 * (2 * 3) and (1 * 2) * 3 must hold, which is called associative.

scala> semigroup.laws[Int @@ Tags.Multiplication].check
+ semigroup.associative: OK, passed 100 tests.

Monoid Laws 

Here are the Monoid Laws:

  /**
   * Monoid instances must satisfy [[scalaz.Semigroup.SemigroupLaw]] and 2 additional laws:
   *
   *  - '''left identity''': `forall a. append(zero, a) == a`
   *  - '''right identity''' : `forall a. append(a, zero) == a`
   */
  trait MonoidLaw extends SemigroupLaw {
    def leftIdentity(a: F)(implicit F: Equal[F]) = F.equal(a, append(zero, a))
    def rightIdentity(a: F)(implicit F: Equal[F]) = F.equal(a, append(a, zero))
  }

This law is simple. I can |+| (mappend) identity value to either left hand side or right hand side. For multiplication:

scala> 1 * 2 assert_=== 2

scala> 2 * 1 assert_=== 2

Using Scalaz:

scala> (Monoid[Int @@ Tags.Multiplication].zero |+| Tags.Multiplication(2): Int) assert_=== 2

scala> (Tags.Multiplication(2) |+| Monoid[Int @@ Tags.Multiplication].zero: Int) assert_=== 2

scala> monoid.laws[Int @@ Tags.Multiplication].check
+ monoid.semigroup.associative: OK, passed 100 tests.
+ monoid.left identity: OK, passed 100 tests.
+ monoid.right identity: OK, passed 100 tests.

Option as Monoid 

LYAHFGG:

One way is to treat Maybe a as a monoid only if its type parameter a is a monoid as well and then implement mappend in such a way that it uses the mappend operation of the values that are wrapped with Just.

Let’s see if this is how Scalaz does it. See std/Option.scala:

  implicit def optionMonoid[A: Semigroup]: Monoid[Option[A]] = new Monoid[Option[A]] {
    def append(f1: Option[A], f2: => Option[A]) = (f1, f2) match {
      case (Some(a1), Some(a2)) => Some(Semigroup[A].append(a1, a2))
      case (Some(a1), None)     => f1
      case (None, Some(a2))     => f2
      case (None, None)         => None
    }

    def zero: Option[A] = None
  }

The implementation is nice and simple. Context bound A: Semigroup says that A must support |+|. The rest is pattern matching. Doing exactly what the book says.

scala> (none: Option[String]) |+| "andy".some
res23: Option[String] = Some(andy)

scala> (Ordering.LT: Ordering).some |+| none
res25: Option[scalaz.Ordering] = Some(LT)

It works.

LYAHFGG:

But if we don’t know if the contents are monoids, we can’t use mappend between them, so what are we to do? Well, one thing we can do is to just discard the second value and keep the first one. For this, the First a type exists.

Haskell is using newtype to implement First type constructor. Scalaz 7 does it using mightly Tagged type:

scala> Tags.First('a'.some) |+| Tags.First('b'.some)
res26: scalaz.@@[Option[Char],scalaz.Tags.First] = Some(a)

scala> Tags.First(none: Option[Char]) |+| Tags.First('b'.some)
res27: scalaz.@@[Option[Char],scalaz.Tags.First] = Some(b)

scala> Tags.First('a'.some) |+| Tags.First(none: Option[Char])
res28: scalaz.@@[Option[Char],scalaz.Tags.First] = Some(a)

LYAHFGG:

If we want a monoid on Maybe a such that the second parameter is kept if both parameters of mappend are Just values, Data.Monoid provides a the Last a type.

This is Tags.Last:

scala> Tags.Last('a'.some) |+| Tags.Last('b'.some)
res29: scalaz.@@[Option[Char],scalaz.Tags.Last] = Some(b)

scala> Tags.Last(none: Option[Char]) |+| Tags.Last('b'.some)
res30: scalaz.@@[Option[Char],scalaz.Tags.Last] = Some(b)

scala> Tags.Last('a'.some) |+| Tags.Last(none: Option[Char])
res31: scalaz.@@[Option[Char],scalaz.Tags.Last] = Some(a)

Foldable 

LYAHFGG:

Because there are so many data structures that work nicely with folds, the Foldable type class was introduced. Much like Functor is for things that can be mapped over, Foldable is for things that can be folded up!

The equivalent in Scalaz is also called Foldable. Let’s see the typeclass contract:

trait Foldable[F[_]] { self =>
  /** Map each element of the structure to a [[scalaz.Monoid]], and combine the results. */
  def foldMap[A,B](fa: F[A])(f: A => B)(implicit F: Monoid[B]): B

  /**Right-associative fold of a structure. */
  def foldRight[A, B](fa: F[A], z: => B)(f: (A, => B) => B): B

  ...
}

Here are the operators:

/** Wraps a value `self` and provides methods related to `Foldable` */
trait FoldableOps[F[_],A] extends Ops[F[A]] {
  implicit def F: Foldable[F]
  ////
  final def foldMap[B: Monoid](f: A => B = (a: A) => a): B = F.foldMap(self)(f)
  final def foldRight[B](z: => B)(f: (A, => B) => B): B = F.foldRight(self, z)(f)
  final def foldLeft[B](z: B)(f: (B, A) => B): B = F.foldLeft(self, z)(f)
  final def foldRightM[G[_], B](z: => B)(f: (A, => B) => G[B])(implicit M: Monad[G]): G[B] = F.foldRightM(self, z)(f)
  final def foldLeftM[G[_], B](z: B)(f: (B, A) => G[B])(implicit M: Monad[G]): G[B] = F.foldLeftM(self, z)(f)
  final def foldr[B](z: => B)(f: A => (=> B) => B): B = F.foldr(self, z)(f)
  final def foldl[B](z: B)(f: B => A => B): B = F.foldl(self, z)(f)
  final def foldrM[G[_], B](z: => B)(f: A => ( => B) => G[B])(implicit M: Monad[G]): G[B] = F.foldrM(self, z)(f)
  final def foldlM[G[_], B](z: B)(f: B => A => G[B])(implicit M: Monad[G]): G[B] = F.foldlM(self, z)(f)
  final def foldr1(f: (A, => A) => A): Option[A] = F.foldr1(self)(f)
  final def foldl1(f: (A, A) => A): Option[A] = F.foldl1(self)(f)
  final def sumr(implicit A: Monoid[A]): A = F.foldRight(self, A.zero)(A.append)
  final def suml(implicit A: Monoid[A]): A = F.foldLeft(self, A.zero)(A.append(_, _))
  final def toList: List[A] = F.toList(self)
  final def toIndexedSeq: IndexedSeq[A] = F.toIndexedSeq(self)
  final def toSet: Set[A] = F.toSet(self)
  final def toStream: Stream[A] = F.toStream(self)
  final def all(p: A => Boolean): Boolean = F.all(self)(p)
  final def ∀(p: A => Boolean): Boolean = F.all(self)(p)
  final def allM[G[_]: Monad](p: A => G[Boolean]): G[Boolean] = F.allM(self)(p)
  final def anyM[G[_]: Monad](p: A => G[Boolean]): G[Boolean] = F.anyM(self)(p)
  final def any(p: A => Boolean): Boolean = F.any(self)(p)
  final def ∃(p: A => Boolean): Boolean = F.any(self)(p)
  final def count: Int = F.count(self)
  final def maximum(implicit A: Order[A]): Option[A] = F.maximum(self)
  final def minimum(implicit A: Order[A]): Option[A] = F.minimum(self)
  final def longDigits(implicit d: A <:< Digit): Long = F.longDigits(self)
  final def empty: Boolean = F.empty(self)
  final def element(a: A)(implicit A: Equal[A]): Boolean = F.element(self, a)
  final def splitWith(p: A => Boolean): List[List[A]] = F.splitWith(self)(p)
  final def selectSplit(p: A => Boolean): List[List[A]] = F.selectSplit(self)(p)
  final def collapse[X[_]](implicit A: ApplicativePlus[X]): X[A] = F.collapse(self)
  final def concatenate(implicit A: Monoid[A]): A = F.fold(self)
  final def traverse_[M[_]:Applicative](f: A => M[Unit]): M[Unit] = F.traverse_(self)(f)

  ////
}

That was impressive. Looks almost like the collection libraries, except it’s taking advantage of typeclasses like Order. Let’s try folding:

scala> List(1, 2, 3).foldRight (1) {_ * _}
res49: Int = 6

scala> 9.some.foldLeft(2) {_ + _}
res50: Int = 11

These are already in the standard library. Let’s try the foldMap operator. Monoid[A] gives us zero and |+|, so that’s enough information to fold things over. Since we can’t assume that Foldable contains a monoid we need a function to change from A => B where [B: Monoid]:

scala> List(1, 2, 3) foldMap {identity}
res53: Int = 6

scala> List(true, false, true, true) foldMap {Tags.Disjunction.apply}
res56: scalaz.@@[Boolean,scalaz.Tags.Disjunction] = true

This surely beats writing Tags.Disjunction(true) for each of them and connecting them with |+|.

We will pick it up from here later. I’ll be out on a business trip, it might slow down.

day 5 

On day 4 we reviewed typeclass laws like Functor laws and used ScalaCheck to validate on arbitrary examples of a typeclass. We also looked at three different ways of using Option as Monoid, and looked at Foldable that can foldMap etc.

A fist full of Monads 

We get to start a new chapter today on Learn You a Haskell for Great Good.

Monads are a natural extension applicative functors, and they provide a solution to the following problem: If we have a value with context, m a, how do we apply it to a function that takes a normal a and returns a value with a context.

The equivalent is called Monad in Scalaz. Here’s the typeclass contract:

trait Monad[F[_]] extends Applicative[F] with Bind[F] { self =>
  ////
}

It extends Applicative and Bind. So let’s look at Bind.

Bind 

Here’s Bind’s contract:

trait Bind[F[_]] extends Apply[F] { self =>
  /** Equivalent to `join(map(fa)(f))`. */
  def bind[A, B](fa: F[A])(f: A => F[B]): F[B]
}

And here are the operators:

/** Wraps a value `self` and provides methods related to `Bind` */
trait BindOps[F[_],A] extends Ops[F[A]] {
  implicit def F: Bind[F]
  ////
  import Liskov.<~<

  def flatMap[B](f: A => F[B]) = F.bind(self)(f)
  def >>=[B](f: A => F[B]) = F.bind(self)(f)
  def ∗[B](f: A => F[B]) = F.bind(self)(f)
  def join[B](implicit ev: A <~< F[B]): F[B] = F.bind(self)(ev(_))
  def μ[B](implicit ev: A <~< F[B]): F[B] = F.bind(self)(ev(_))
  def >>[B](b: F[B]): F[B] = F.bind(self)(_ => b)
  def ifM[B](ifTrue: => F[B], ifFalse: => F[B])(implicit ev: A <~< Boolean): F[B] = {
    val value: F[Boolean] = Liskov.co[F, A, Boolean](ev)(self)
    F.ifM(value, ifTrue, ifFalse)
  }
  ////
}

It introduces flatMap operator and its symbolic aliases >>= and ∗. We’ll worry about the other operators later. We are use to flapMap from the standard library:

scala> 3.some flatMap { x => (x + 1).some }
res2: Option[Int] = Some(4)

scala> (none: Option[Int]) flatMap { x => (x + 1).some }
res3: Option[Int] = None

Monad 

Back to Monad:

trait Monad[F[_]] extends Applicative[F] with Bind[F] { self =>
  ////
}

Unlike Haskell, Monad[F[_]] exntends Applicative[F[_]] so there’s no return vs pure issues. They both use point.

scala> Monad[Option].point("WHAT")
res5: Option[String] = Some(WHAT)

scala> 9.some flatMap { x => Monad[Option].point(x * 10) }
res6: Option[Int] = Some(90)

scala> (none: Option[Int]) flatMap { x => Monad[Option].point(x * 10) }
res7: Option[Int] = None

Walk the line 

LYAHFGG:

Let’s say that [Pierre] keeps his balance if the number of birds on the left side of the pole and on the right side of the pole is within three. So if there’s one bird on the right side and four birds on the left side, he’s okay. But if a fifth bird lands on the left side, then he loses his balance and takes a dive.

Now let’s try implementing Pole example from the book.

scala> type Birds = Int
defined type alias Birds

scala> case class Pole(left: Birds, right: Birds)
defined class Pole

I don’t think it’s common to alias Int like this in Scala, but we’ll go with the flow. I am going to turn Pole into a case class so I can implement landLeft and landRight as methods:

scala> case class Pole(left: Birds, right: Birds) {
         def landLeft(n: Birds): Pole = copy(left = left + n)
         def landRight(n: Birds): Pole = copy(right = right + n)
       }
defined class Pole

I think it looks better with some OO:

scala> Pole(0, 0).landLeft(2)
res10: Pole = Pole(2,0)

scala> Pole(1, 2).landRight(1)
res11: Pole = Pole(1,3)

scala> Pole(1, 2).landRight(-1)
res12: Pole = Pole(1,1)

We can chain these too:

scala> Pole(0, 0).landLeft(1).landRight(1).landLeft(2)
res13: Pole = Pole(3,1)

scala> Pole(0, 0).landLeft(1).landRight(4).landLeft(-1).landRight(-2)
res15: Pole = Pole(0,2)

As the book says, an intermediate value have failed but the calculation kept going. Now let’s introduce failures as Option[Pole]:

scala> case class Pole(left: Birds, right: Birds) {
         def landLeft(n: Birds): Option[Pole] =
           if (math.abs((left + n) - right) < 4) copy(left = left + n).some
           else none
         def landRight(n: Birds): Option[Pole] =
           if (math.abs(left - (right + n)) < 4) copy(right = right + n).some
           else none
       }
defined class Pole


scala> Pole(0, 0).landLeft(2)
res16: Option[Pole] = Some(Pole(2,0))

scala> Pole(0, 3).landLeft(10)
res17: Option[Pole] = None

Let’s try the chaining using flatMap:

scala> Pole(0, 0).landRight(1) flatMap {_.landLeft(2)}
res18: Option[Pole] = Some(Pole(2,1))

scala> (none: Option[Pole]) flatMap {_.landLeft(2)}
res19: Option[Pole] = None

scala> Monad[Option].point(Pole(0, 0)) flatMap {_.landRight(2)} flatMap {_.landLeft(2)} flatMap {_.landRight(2)}
res21: Option[Pole] = Some(Pole(2,4))

Note the use of Monad[Option].point(...) here to start the initial value in Option context. We can also try the >>= alias to make it look more monadic:

scala> Monad[Option].point(Pole(0, 0)) >>= {_.landRight(2)} >>= {_.landLeft(2)} >>= {_.landRight(2)}
res22: Option[Pole] = Some(Pole(2,4))

Let’s see if monadic chaining simulates the pole balancing better:

scala> Monad[Option].point(Pole(0, 0)) >>= {_.landLeft(1)} >>= {_.landRight(4)} >>= {_.landLeft(-1)} >>= {_.landRight(-2)}
res23: Option[Pole] = None

It works.

Banana on wire 

LYAHFGG:

We may also devise a function that ignores the current number of birds on the balancing pole and just makes Pierre slip and fall. We can call it banana.

Here’s the banana that always fails:

scala> case class Pole(left: Birds, right: Birds) {
         def landLeft(n: Birds): Option[Pole] =
           if (math.abs((left + n) - right) < 4) copy(left = left + n).some
           else none
         def landRight(n: Birds): Option[Pole] =
           if (math.abs(left - (right + n)) < 4) copy(right = right + n).some
           else none
         def banana: Option[Pole] = none
       }
defined class Pole

scala> Monad[Option].point(Pole(0, 0)) >>= {_.landLeft(1)} >>= {_.banana} >>= {_.landRight(1)}
res24: Option[Pole] = None

LYAHFGG:

Instead of making functions that ignore their input and just return a predetermined monadic value, we can use the >> function.

Here’s how >> behaves with Option:

scala> (none: Option[Int]) >> 3.some
res25: Option[Int] = None

scala> 3.some >> 4.some
res26: Option[Int] = Some(4)

scala> 3.some >> (none: Option[Int])
res27: Option[Int] = None

Let’s try replacing banana with >> (none: Option[Pole]):

scala> Monad[Option].point(Pole(0, 0)) >>= {_.landLeft(1)} >> (none: Option[Pole]) >>= {_.landRight(1)}
<console>:26: error: missing parameter type for expanded function ((x$1) => x$1.landLeft(1))
              Monad[Option].point(Pole(0, 0)) >>= {_.landLeft(1)} >> (none: Option[Pole]) >>= {_.landRight(1)}
                                                   ^

The type inference broke down all the sudden. The problem is likely the operator precedence. Programming in Scala says:

The one exception to the precedence rule, alluded to above, concerns assignment operators, which end in an equals character. If an operator ends in an equals character (=), and the operator is not one of the comparison operators <=, >=, ==, or !=, then the precedence of the operator is the same as that of simple assignment (=). That is, it is lower than the precedence of any other operator.

Note: The above description is incomplete. Another exception from the assignment operator rule is if it starts with (=) like ===.

Because >>= (bind) ends in equals character, its precedence is the lowest, which forces ({_.landLeft(1)} >> (none: Option[Pole])) to evaluate first. There are a few unpalatable work arounds. First we can use dot-and-parens like normal method calls:

scala> Monad[Option].point(Pole(0, 0)).>>=({_.landLeft(1)}).>>(none: Option[Pole]).>>=({_.landRight(1)})
res9: Option[Pole] = None

Or recognize the precedence issue and place parens around just the right place:

scala> (Monad[Option].point(Pole(0, 0)) >>= {_.landLeft(1)}) >> (none: Option[Pole]) >>= {_.landRight(1)}
res10: Option[Pole] = None

Both yield the right result. By the way, changing >>= to flatMap is not going to help since >> still has higher precedence.

for syntax 

LYAHFGG:

Monads in Haskell are so useful that they got their own special syntax called do notation.

First, let write the nested lambda:

scala> 3.some >>= { x => "!".some >>= { y => (x.shows + y).some } }
res14: Option[String] = Some(3!)

By using >>=, any part of the calculation can fail:

scala> 3.some >>= { x => (none: Option[String]) >>= { y => (x.shows + y).some } }
res17: Option[String] = None

scala> (none: Option[Int]) >>= { x => "!".some >>= { y => (x.shows + y).some } }
res16: Option[String] = None

scala> 3.some >>= { x => "!".some >>= { y => (none: Option[String]) } }
res18: Option[String] = None

Instead of the do notation in Haskell, Scala has for syntax, which does the same thing:

scala> for {
         x <- 3.some
         y <- "!".some
       } yield (x.shows + y)
res19: Option[String] = Some(3!)

LYAHFGG:

In a do expression, every line that isn’t a let line is a monadic value.

I think this applies true for Scala’s for syntax too.

Pierre returns 

LYAHFGG:

Our tightwalker’s routine can also be expressed with do notation.

scala> def routine: Option[Pole] =
         for {
           start <- Monad[Option].point(Pole(0, 0))
           first <- start.landLeft(2)
           second <- first.landRight(2)
           third <- second.landLeft(1)
         } yield third
routine: Option[Pole]

scala> routine
res20: Option[Pole] = Some(Pole(3,2))

We had to extract third since yield expects Pole not Option[Pole].

LYAHFGG:

If we want to throw the Pierre a banana peel in do notation, we can do the following:

scala> def routine: Option[Pole] =
         for {
           start <- Monad[Option].point(Pole(0, 0))
           first <- start.landLeft(2)
           _ <- (none: Option[Pole])
           second <- first.landRight(2)
           third <- second.landLeft(1)
         } yield third
routine: Option[Pole]

scala> routine
res23: Option[Pole] = None

Pattern matching and failure 

LYAHFGG:

In do notation, when we bind monadic values to names, we can utilize pattern matching, just like in let expressions and function parameters.

scala> def justH: Option[Char] =
         for {
           (x :: xs) <- "hello".toList.some
         } yield x
justH: Option[Char]

scala> justH
res25: Option[Char] = Some(h)

When pattern matching fails in a do expression, the fail function is called. It’s part of the Monad type class and it enables failed pattern matching to result in a failure in the context of the current monad instead of making our program crash.

scala> def wopwop: Option[Char] =
         for {
           (x :: xs) <- "".toList.some
         } yield x
wopwop: Option[Char]

scala> wopwop
res28: Option[Char] = None

The failed pattern matching returns None here. This is an interesting aspect of for syntax that I haven’t thought about, but totally makes sense.

List Monad 

LYAHFGG:

On the other hand, a value like [3,8,9] contains several results, so we can view it as one value that is actually many values at the same time. Using lists as applicative functors showcases this non-determinism nicely.

Let’s look at using List as Applicatives again:

scala> ^(List(1, 2, 3), List(10, 100, 100)) {_ * _}
res29: List[Int] = List(10, 100, 100, 20, 200, 200, 30, 300, 300)

let’s try feeding a non-deterministic value to a function:

scala> List(3, 4, 5) >>= {x => List(x, -x)}
res30: List[Int] = List(3, -3, 4, -4, 5, -5)

So in this monadic view, List context represent mathematical value that could have multiple solutions. Other than that manipulating Lists using for notation is just like plain Scala:

scala> for {
         n <- List(1, 2)
         ch <- List('a', 'b')
       } yield (n, ch)
res33: List[(Int, Char)] = List((1,a), (1,b), (2,a), (2,b))

MonadPlus and the guard function 

Scala’s for notation allows filtering:

scala> for {
         x <- 1 |-> 50 if x.shows contains '7'
       } yield x
res40: List[Int] = List(7, 17, 27, 37, 47)

LYAHFGG:

The MonadPlus type class is for monads that can also act as monoids.

Here’s the typeclass contract for MonadPlus:

trait MonadPlus[F[_]] extends Monad[F] with ApplicativePlus[F] { self =>
  ...
}

Plus, PlusEmpty, and ApplicativePlus 

It extends ApplicativePlus:

trait ApplicativePlus[F[_]] extends Applicative[F] with PlusEmpty[F] { self =>
  ...
}

And that extends PlusEmpty:

trait PlusEmpty[F[_]] extends Plus[F] { self =>
  ////
  def empty[A]: F[A]
}

And that extends Plus:

trait Plus[F[_]]  { self =>
  def plus[A](a: F[A], b: => F[A]): F[A]
}

Similar to Semigroup[A] and Monoid[A], Plus[F[_]] and PlusEmpty[F[_]] requires their instances to implement plus and empty, but at the type constructor ( F[_]) level.

Plus introduces <+> operator to append two containers:

scala> List(1, 2, 3) <+> List(4, 5, 6)
res43: List[Int] = List(1, 2, 3, 4, 5, 6)

MonadPlus again 

MonadPlus introduces filter operation.

scala> (1 |-> 50) filter { x => x.shows contains '7' }
res46: List[Int] = List(7, 17, 27, 37, 47)

A knight’s quest 

LYAHFGG:

Here’s a problem that really lends itself to being solved with non-determinism. Say you have a chess board and only one knight piece on it. We want to find out if the knight can reach a certain position in three moves.

Instead of type aliasing a pair, let’s make this into a case class again:

scala> case class KnightPos(c: Int, r: Int)
defined class KnightPos

Heres the function to calculate all of his next next positions:

scala> case class KnightPos(c: Int, r: Int) {
         def move: List[KnightPos] =
           for {
             KnightPos(c2, r2) <- List(KnightPos(c + 2, r - 1), KnightPos(c + 2, r + 1),
               KnightPos(c - 2, r - 1), KnightPos(c - 2, r + 1),
               KnightPos(c + 1, r - 2), KnightPos(c + 1, r + 2),
               KnightPos(c - 1, r - 2), KnightPos(c - 1, r + 2)) if (
               ((1 |-> 8) contains c2) && ((1 |-> 8) contains r2))
           } yield KnightPos(c2, r2)
       }
defined class KnightPos

scala> KnightPos(6, 2).move
res50: List[KnightPos] = List(KnightPos(8,1), KnightPos(8,3), KnightPos(4,1), KnightPos(4,3), KnightPos(7,4), KnightPos(5,4))

scala> KnightPos(8, 1).move
res51: List[KnightPos] = List(KnightPos(6,2), KnightPos(7,3))

The answers look good. Now we implement chaining this three times:

scala> case class KnightPos(c: Int, r: Int) {
         def move: List[KnightPos] =
           for {
             KnightPos(c2, r2) <- List(KnightPos(c + 2, r - 1), KnightPos(c + 2, r + 1),
             KnightPos(c - 2, r - 1), KnightPos(c - 2, r + 1),
             KnightPos(c + 1, r - 2), KnightPos(c + 1, r + 2),
             KnightPos(c - 1, r - 2), KnightPos(c - 1, r + 2)) if (
             ((1 |-> 8) element c2) && ((1 |-> 8) contains r2))
           } yield KnightPos(c2, r2)
         def in3: List[KnightPos] =
           for {
             first <- move
             second <- first.move
             third <- second.move
           } yield third
         def canReachIn3(end: KnightPos): Boolean = in3 contains end
       }
defined class KnightPos

scala> KnightPos(6, 2) canReachIn3 KnightPos(6, 1)
res56: Boolean = true

scala> KnightPos(6, 2) canReachIn3 KnightPos(7, 3)
res57: Boolean = false

Monad laws 

Left identity 

LYAHFGG:

The first monad law states that if we take a value, put it in a default context with return and then feed it to a function by using >>=, it’s the same as just taking the value and applying the function to it.

To put this in Scala,

// (Monad[F].point(x) flatMap {f}) assert_=== f(x)

scala> (Monad[Option].point(3) >>= { x => (x + 100000).some }) assert_=== 3 |> { x => (x + 100000).some }

Right identity 

The second law states that if we have a monadic value and we use >>= to feed it to return, the result is our original monadic value.

// (m forMap {Monad[F].point(_)}) assert_=== m

scala> ("move on up".some flatMap {Monad[Option].point(_)}) assert_=== "move on up".some

Associativity 

The final monad law says that when we have a chain of monadic function applications with >>=, it shouldn’t matter how they’re nested.

// (m flatMap f) flatMap g assert_=== m flatMap { x => f(x) flatMap {g} }

scala> Monad[Option].point(Pole(0, 0)) >>= {_.landRight(2)} >>= {_.landLeft(2)} >>= {_.landRight(2)}
res76: Option[Pole] = Some(Pole(2,4))

scala> Monad[Option].point(Pole(0, 0)) >>= { x =>
       x.landRight(2) >>= { y =>
       y.landLeft(2) >>= { z =>
       z.landRight(2)
       }}}
res77: Option[Pole] = Some(Pole(2,4))

Scalaz 7 expresses these laws as the following:

  trait MonadLaw extends ApplicativeLaw {
    /** Lifted `point` is a no-op. */
    def rightIdentity[A](a: F[A])(implicit FA: Equal[F[A]]): Boolean = FA.equal(bind(a)(point(_: A)), a)
    /** Lifted `f` applied to pure `a` is just `f(a)`. */
    def leftIdentity[A, B](a: A, f: A => F[B])(implicit FB: Equal[F[B]]): Boolean = FB.equal(bind(point(a))(f), f(a))
    /**
     * As with semigroups, monadic effects only change when their
     * order is changed, not when the order in which they're
     * combined changes.
     */
    def associativeBind[A, B, C](fa: F[A], f: A => F[B], g: B => F[C])(implicit FC: Equal[F[C]]): Boolean =
      FC.equal(bind(bind(fa)(f))(g), bind(fa)((a: A) => bind(f(a))(g)))
  }

Here’s how to check if Option conforms to the Monad laws. Run sbt test:console with build.sbt we used in day 4:

scala> monad.laws[Option].check
+ monad.applicative.functor.identity: OK, passed 100 tests.
+ monad.applicative.functor.associative: OK, passed 100 tests.
+ monad.applicative.identity: OK, passed 100 tests.
+ monad.applicative.composition: OK, passed 100 tests.
+ monad.applicative.homomorphism: OK, passed 100 tests.
+ monad.applicative.interchange: OK, passed 100 tests.
+ monad.right identity: OK, passed 100 tests.
+ monad.left identity: OK, passed 100 tests.
+ monad.associativity: OK, passed 100 tests.

Looking good, Option. We’ll pick it up from here.

day 6 

Yesterday we looked at Monad typeclass, which introduces flatMap. We looked at how monadic chaining can add contexts to values. Because both Option and List already have flatMap in the standard library, it was more about changing the way we see things rather than introducing new code. We also reviewed for syntax as a way of chaining monadic operations.

for syntax again 

There’s a subtle difference in Haskell’s do notation and Scala’s for syntax. Here’s an example of do notation:

foo = do
  x <- Just 3
  y <- Just "!"
  Just (show x ++ y)

Typically one would write return (show x ++ y), but I wrote out Just, so it’s clear that the last line is a monadic value. On the other hand, Scala would look as follows:

scala> def foo = for {
         x <- 3.some
         y <- "!".some
       } yield x.shows + y

Looks almost the same, but in Scala x.shows + y is plain String, and yield forces the value to get in the context. This is great if we have the raw value. But what if there’s a function that returns monadic value?

in3 start = do
  first <- moveKnight start
  second <- moveKnight first
  moveKnight second

We can’t write this in Scala without extract the value from moveKnight second and re-wrapping it using yeild:

def in3: List[KnightPos] = for {
  first <- move
  second <- first.move
  third <- second.move
} yield third

This difference shouldn’t pose much problem in practice, but it’s something to keep in mind.

Writer? I hardly knew her! 

Learn You a Haskell for Great Good says:

Whereas the Maybe monad is for values with an added context of failure, and the list monad is for nondeterministic values, Writer monad is for values that have another value attached that acts as a sort of log value.

Let’s follow the book and implement applyLog function:

scala> def isBigGang(x: Int): (Boolean, String) =
         (x > 9, "Compared gang size to 9.")
isBigGang: (x: Int)(Boolean, String)

scala> implicit class PairOps[A](pair: (A, String)) {
         def applyLog[B](f: A => (B, String)): (B, String) = {
           val (x, log) = pair
           val (y, newlog) = f(x)
           (y, log ++ newlog)
         }
       }
defined class PairOps

scala> (3, "Smallish gang.") applyLog isBigGang
res30: (Boolean, String) = (false,Smallish gang.Compared gang size to 9.)

Since method injection is a common use case for implicits, Scala 2.10 adds a syntax sugar called implicit class to make the promotion from a class to an enriched class easier. Here’s how we can generalize the log to a Monoid:

scala> implicit class PairOps[A, B: Monoid](pair: (A, B)) {
         def applyLog[C](f: A => (C, B)): (C, B) = {
           val (x, log) = pair
           val (y, newlog) = f(x)
           (y, log |+| newlog)
         }
       }
defined class PairOps

scala> (3, "Smallish gang.") applyLog isBigGang
res31: (Boolean, String) = (false,Smallish gang.Compared gang size to 9.)

Writer 

LYAHFGG:

To attach a monoid to a value, we just need to put them together in a tuple. The Writer w a type is just a newtype wrapper for this.

In Scalaz, the equivalent is called Writer:

type Writer[+W, +A] = WriterT[Id, W, A]

Writer[+W, +A] is a type alias for WriterT[Id, W, A].

WriterT 

Here’s the simplified version of WriterT:

sealed trait WriterT[F[+_], +W, +A] { self =>
  val run: F[(W, A)]

  def written(implicit F: Functor[F]): F[W] =
    F.map(run)(_._1)
  def value(implicit F: Functor[F]): F[A] =
    F.map(run)(_._2)
}

It wasn’t immediately obvious to me how a writer is actually created at first, but eventually figured it out:

scala> 3.set("Smallish gang.")
res46: scalaz.Writer[String,Int] = scalaz.WriterTFunctions$$anon$26@477a0c05

The following operators are supported by all data types enabled by import Scalaz._:

trait ToDataOps extends ToIdOps with ToTreeOps with ToWriterOps with ToValidationOps with ToReducerOps with ToKleisliOps

The operator in question is part of WriterOps:

final class WriterOps[A](self: A) {
  def set[W](w: W): Writer[W, A] = WriterT.writer(w -> self)

  def tell: Writer[A, Unit] = WriterT.tell(self)
}

The above methods are injected to all types so we can use them to create Writers:

scala> 3.set("something")
res57: scalaz.Writer[String,Int] = scalaz.WriterTFunctions$$anon$26@159663c3

scala> "something".tell
res58: scalaz.Writer[String,Unit] = scalaz.WriterTFunctions$$anon$26@374de9cf

What if we want to get the identity value like return 3 :: Writer String Int? Monad[F[_]] expects a type constructor with one parameter, but Writer[+W, +A] takes two. There’s a helper type in Scalaz called MonadTell (in scalaz 7.0 it was MonadWriter) to help us out:

scala> MonadTell[Writer, String]
res62: scalaz.MonadTell[scalaz.Writer,String] = scalaz.WriterTInstances$$anon$1@6b8501fa

scala> MonadTell[Writer, String].point(3).run
res64: (String, Int) = ("",3)

Using for syntax with Writer 

LYAHFGG:

Now that we have a Monad instance, we’re free to use do notation for Writer values.

Let’s implement the example in Scala:

scala> def logNumber(x: Int): Writer[List[String], Int] =
         x.set(List("Got number: " + x.shows))
logNumber: (x: Int)scalaz.Writer[List[String],Int]

scala> def multWithLog: Writer[List[String], Int] = for {
         a <- logNumber(3)
         b <- logNumber(5)
       } yield a * b
multWithLog: scalaz.Writer[List[String],Int]

scala> multWithLog run
res67: (List[String], Int) = (List(Got number: 3, Got number: 5),15)

Adding logging to program 

Here’s the gcd example:

scala> :paste
// Entering paste mode (ctrl-D to finish)

def gcd(a: Int, b: Int): Writer[List[String], Int] =
  if (b == 0) for {
      _ <- List("Finished with " + a.shows).tell
    } yield a
  else
    List(a.shows + " mod " + b.shows + " = " + (a % b).shows).tell >>= { _ =>
      gcd(b, a % b)
    }

// Exiting paste mode, now interpreting.

gcd: (a: Int, b: Int)scalaz.Writer[List[String],Int]

scala> gcd(8, 3).run
res71: (List[String], Int) = (List(8 mod 3 = 2, 3 mod 2 = 1, 2 mod 1 = 0, Finished with 1),1)

Inefficient List construction 

LYAHFGG:

When using the Writer monad, you have to be careful which monoid to use, because using lists can sometimes turn out to be very slow. That’s because lists use ++ for mappend and using ++ to add something to the end of a list is slow if that list is really long.

Here’s the table of performance characteristics for major collections. What stands out for immutable collection is Vector since it has effective constant for all operations. Vector is a tree structure with the branching factor of 32, and it’s able to achieve fast updates by structure sharing.

scala> Monoid[Vector[String]]
res73: scalaz.Monoid[Vector[String]] = scalaz.std.IndexedSeqSubInstances$$anon$4@6f82f06f

Here’s the vector version of gcd:

scala> :paste
// Entering paste mode (ctrl-D to finish)

def gcd(a: Int, b: Int): Writer[Vector[String], Int] =
  if (b == 0) for {
      _ <- Vector("Finished with " + a.shows).tell
    } yield a
  else for {
      result <- gcd(b, a % b)
      _ <- Vector(a.shows + " mod " + b.shows + " = " + (a % b).shows).tell
    } yield result

// Exiting paste mode, now interpreting.

gcd: (a: Int, b: Int)scalaz.Writer[Vector[String],Int]

scala> gcd(8, 3).run
res74: (Vector[String], Int) = (Vector(Finished with 1, 2 mod 1 = 0, 3 mod 2 = 1, 8 mod 3 = 2),1)

Comparing performance 

Like the book let’s write a microbenchmark to compare the performance:

def vectorFinalCountDown(x: Int): Writer[Vector[String], Unit] = {
  import annotation.tailrec
  @tailrec def doFinalCountDown(x: Int, w: Writer[Vector[String], Unit]): Writer[Vector[String], Unit] = x match {
    case 0 => w >>= { _ => Vector("0").tell }
    case x => doFinalCountDown(x - 1, w >>= { _ =>
      Vector(x.shows).tell
    })
  }
  val t0 = System.currentTimeMillis
  val r = doFinalCountDown(x, Vector[String]().tell)
  val t1 = System.currentTimeMillis
  r >>= { _ => Vector((t1 - t0).shows + " msec").tell }
}

def listFinalCountDown(x: Int): Writer[List[String], Unit] = {
  import annotation.tailrec
  @tailrec def doFinalCountDown(x: Int, w: Writer[List[String], Unit]): Writer[List[String], Unit] = x match {
    case 0 => w >>= { _ => List("0").tell }
    case x => doFinalCountDown(x - 1, w >>= { _ =>
      List(x.shows).tell
    })
  }
  val t0 = System.currentTimeMillis
  val r = doFinalCountDown(x, List[String]().tell)
  val t1 = System.currentTimeMillis
  r >>= { _ => List((t1 - t0).shows + " msec").tell }
}

We can now run this as follows:

scala> vectorFinalCountDown(10000).run
res18: (Vector[String], Unit) = (Vector(10000, 9999, 9998, 9997, 9996, 9995, 9994, 9993, 9992, 9991, 9990, 9989, 9988, 9987, 9986, 9985, 9984, ...

scala> res18._1.last
res19: String = 1206 msec

scala> listFinalCountDown(10000).run
res20: (List[String], Unit) = (List(10000, 9999, 9998, 9997, 9996, 9995, 9994, 9993, 9992, 9991, 9990, 9989, 9988, 9987, 9986, 9985, 9984, ...
scala> res20._1.last

res21: String = 2050 msec

As you can see List is taking almost double the time.

Reader 

LYAHFGG:

In the chapter about applicatives, we saw that the function type, (->) r is an instance of Functor.

scala> val f = (_: Int) * 5
f: Int => Int = <function1>

scala> val g = (_: Int) + 3
g: Int => Int = <function1>

scala> (g map f)(8)
res22: Int = 55

We’ve also seen that functions are applicative functors. They allow us to operate on the eventual results of functions as if we already had their results.

scala> val f = ({(_: Int) * 2} |@| {(_: Int) + 10}) {_ + _}
warning: there were 1 deprecation warnings; re-run with -deprecation for details
f: Int => Int = <function1>

scala> f(3)
res35: Int = 19

Not only is the function type (->) r a functor and an applicative functor, but it’s also a monad. Just like other monadic values that we’ve met so far, a function can also be considered a value with a context. The context for functions is that that value is not present yet and that we have to apply that function to something in order to get its result value.

Let’s try implementing the example:

scala> val addStuff: Int => Int = for {
         a <- (_: Int) * 2
         b <- (_: Int) + 10
       } yield a + b
addStuff: Int => Int = <function1>

scala> addStuff(3)
res39: Int = 19

Both (*2) and (+10) get applied to the number 3 in this case. return (a+b) does as well, but it ignores it and always presents a+b as the result. For this reason, the function monad is also called the reader monad. All the functions read from a common source.

Essentially, the reader monad lets us pretend the value is already there. I am guessing that this works only for functions that accepts one parameter. Unlike Option and List monads, neither Writer nor reader monad is available in the standard library. And they look pretty useful.

Let’s pick it up from here later.

day 7 

On day 6 we reviewed for syntax and checked out the Writer monad and the reader monad, which is basically using functions as monads.

Applicative Builder 

One thing I snuck in while covering the reader monad is the Applicative builder |@|. On day 2 we introduced ^(f1, f2) {...} style that was introduced in 7.0.0-M3, but that does not seem to work for functions or any type constructor with two parameters.

The discussion on the Scalaz mailing list seems to suggest that |@| will be undeprecated, so that’s the style we will be using, which looks like this:

scala> (3.some |@| 5.some) {_ + _}
res18: Option[Int] = Some(8)

scala> val f = ({(_: Int) * 2} |@| {(_: Int) + 10}) {_ + _}
f: Int => Int = <function1>

Tasteful stateful computations 

Learn You a Haskell for Great Good says:

Haskell features a thing called the state monad, which makes dealing with stateful problems a breeze while still keeping everything nice and pure.

Let’s implement the stack example. This time I am going to translate Haskell into Scala without making it into case class:

scala> type Stack = List[Int]
defined type alias Stack

scala> def pop(stack: Stack): (Int, Stack) = stack match {
         case x :: xs => (x, xs)
       }
pop: (stack: Stack)(Int, Stack)

scala> def push(a: Int, stack: Stack): (Unit, Stack) = ((), a :: stack)
push: (a: Int, stack: Stack)(Unit, Stack)

scala> def stackManip(stack: Stack): (Int, Stack) = {
         val (_, newStack1) = push(3, stack)
         val (a, newStack2) = pop(newStack1)
         pop(newStack2)
       }
stackManip: (stack: Stack)(Int, Stack)

scala> stackManip(List(5, 8, 2, 1))
res0: (Int, Stack) = (5,List(8, 2, 1))

State and StateT 

LYAHFGG:

We’ll say that a stateful computation is a function that takes some state and returns a value along with some new state. That function would have the following type:

s -> (a, s)

The important thing to note is that unlike the general monads we’ve seen, State specifically wraps functions. Let’s look at State’s definition in Scalaz:

  type State[S, +A] = StateT[Id, S, A]

  // important to define here, rather than at the top-level, to avoid Scala 2.9.2 bug
  object State extends StateFunctions {
    def apply[S, A](f: S => (S, A)): State[S, A] = new StateT[Id, S, A] {
      def apply(s: S) = f(s)
    }
  }

As with Writer, State[S, +A] is a type alias of StateT[Id, S, A]. Here’s the simplified version of StateT:

trait StateT[F[+_], S, +A] { self =>
  /** Run and return the final value and state in the context of `F` */
  def apply(initial: S): F[(S, A)]

  /** An alias for `apply` */
  def run(initial: S): F[(S, A)] = apply(initial)

  /** Calls `run` using `Monoid[S].zero` as the initial state */
  def runZero(implicit S: Monoid[S]): F[(S, A)] =
    run(S.zero)
}

We can construct a new state using State singleton:

scala> State[List[Int], Int] { case x :: xs => (xs, x) }
res1: scalaz.State[List[Int],Int] = scalaz.package$State$$anon$1@19f58949

Let’s try implementing the stack using State:

scala> type Stack = List[Int]
defined type alias Stack

scala> val pop = State[Stack, Int] {
         case x :: xs => (xs, x)
       }
pop: scalaz.State[Stack,Int]

scala> def push(a: Int) = State[Stack, Unit] {
         case xs => (a :: xs, ())
       }
push: (a: Int)scalaz.State[Stack,Unit]

scala> def stackManip: State[Stack, Int] = for {
         _ <- push(3)
         a <- pop
         b <- pop
       } yield(b)
stackManip: scalaz.State[Stack,Int]

scala> stackManip(List(5, 8, 2, 1))
res2: (Stack, Int) = (List(8, 2, 1),5)

Using State[List[Int], Int] {...} we were able to abstract out the “extract state, and return value with a state” portion of the code. The powerful part is the fact that we can monadically chain each operations using for syntax without manually passing around the Stack values as demonstrated in stackManip above.

Getting and setting state 

LYAHFGG:

The Control.Monad.State module provides a type class that’s called MonadState and it features two pretty useful functions, namely get and put.

The State object extends StateFunctions trait, which defines a few helper functions:

trait StateFunctions {
  def constantState[S, A](a: A, s: => S): State[S, A] =
    State((_: S) => (s, a))
  def state[S, A](a: A): State[S, A] =
    State((_ : S, a))
  def init[S]: State[S, S] = State(s => (s, s))
  def get[S]: State[S, S] = init
  def gets[S, T](f: S => T): State[S, T] = State(s => (s, f(s)))
  def put[S](s: S): State[S, Unit] = State(_ => (s, ()))
  def modify[S](f: S => S): State[S, Unit] = State(s => {
    val r = f(s);
    (r, ())
  })
  /**
   * Computes the difference between the current and previous values of `a`
   */
  def delta[A](a: A)(implicit A: Group[A]): State[A, A] = State{
    (prevA) =>
      val diff = A.minus(a, prevA)
      (diff, a)
  }
}

These are confusing at first. But remember State monad encapsulates functions that takes a state and returns a pair of a value and a state. So get in the context of state simply means to retreive the state into the value:

  def init[S]: State[S, S] = State(s => (s, s))
  def get[S]: State[S, S] = init

And put in this context means to put some value into the state:

  def put[S](s: S): State[S, Unit] = State(_ => (s, ()))

To illustrate this point, let’s implement stackyStack function.

scala> def stackyStack: State[Stack, Unit] = for {
         stackNow <- get
         r <- if (stackNow === List(1, 2, 3)) put(List(8, 3, 1))
              else put(List(9, 2, 1))
       } yield r
stackyStack: scalaz.State[Stack,Unit]

scala> stackyStack(List(1, 2, 3))
res4: (Stack, Unit) = (List(8, 3, 1),())

We can also implement pop and push in terms of get and put:

scala> val pop: State[Stack, Int] = for {
         s <- get[Stack]
         val (x :: xs) = s
         _ <- put(xs)
       } yield x
pop: scalaz.State[Stack,Int] = scalaz.StateT$$anon$7@40014da3

scala> def push(x: Int): State[Stack, Unit] = for {
         xs <- get[Stack]
         r <- put(x :: xs)
       } yield r
push: (x: Int)scalaz.State[Stack,Unit]

As you can see a monad on its own doesn’t do much (encapsulate a function that returns a tuple), but by chaining them we can remove some boilerplates.

\/ 

LYAHFGG:

The Either e a type on the other hand, allows us to incorporate a context of possible failure to our values while also being able to attach values to the failure, so that they can describe what went wrong or provide some other useful info regarding the failure.

We know Either[A, B] from the standard library, but Scalaz 7 implements its own Either equivalent named \/:

sealed trait \/[+A, +B] {
  ...
  /** Return `true` if this disjunction is left. */
  def isLeft: Boolean =
    this match {
      case -\/(_) => true
      case \/-(_) => false
    }

  /** Return `true` if this disjunction is right. */
  def isRight: Boolean =
    this match {
      case -\/(_) => false
      case \/-(_) => true
    }
  ...
  /** Flip the left/right values in this disjunction. Alias for `unary_~` */
  def swap: (B \/ A) =
    this match {
      case -\/(a) => \/-(a)
      case \/-(b) => -\/(b)
    }
  /** Flip the left/right values in this disjunction. Alias for `swap` */
  def unary_~ : (B \/ A) = swap
  ...
  /** Return the right value of this disjunction or the given default if left. Alias for `|` */
  def getOrElse[BB >: B](x: => BB): BB =
    toOption getOrElse x
  /** Return the right value of this disjunction or the given default if left. Alias for `getOrElse` */
  def |[BB >: B](x: => BB): BB = getOrElse(x)

  /** Return this if it is a right, otherwise, return the given value. Alias for `|||` */
  def orElse[AA >: A, BB >: B](x: => AA \/ BB): AA \/ BB =
    this match {
      case -\/(_) => x
      case \/-(_) => this
    }
  /** Return this if it is a right, otherwise, return the given value. Alias for `orElse` */
  def |||[AA >: A, BB >: B](x: => AA \/ BB): AA \/ BB = orElse(x)
  ...
}

private case class -\/[+A](a: A) extends (A \/ Nothing)
private case class \/-[+B](b: B) extends (Nothing \/ B)

These values are created using right and left method injected to all data types via IdOps:

scala> 1.right[String]
res12: scalaz.\/[String,Int] = \/-(1)

scala> "error".left[Int]
res13: scalaz.\/[String,Int] = -\/(error)

The Either type in Scala standard library is not a monad on its own, which means it does not implement flatMap method with or without Scalaz:

scala> Left[String, Int]("boom") flatMap { x => Right[String, Int](x + 1) }
<console>:8: error: value flatMap is not a member of scala.util.Left[String,Int]
              Left[String, Int]("boom") flatMap { x => Right[String, Int](x + 1) }
                                        ^

You have to call right method to turn it into RightProjection:

scala> Left[String, Int]("boom").right flatMap { x => Right[String, Int](x + 1)}
res15: scala.util.Either[String,Int] = Left(boom)

This is silly since the point of having Either is to report an error on the left. Scalaz’s \/ assumes that you’d mostly want right projection:

scala> "boom".left[Int] >>= { x => (x + 1).right }
res18: scalaz.Unapply[scalaz.Bind,scalaz.\/[String,Int]]{type M[X] = scalaz.\/[String,X]; type A = Int}#M[Int] = -\/(boom)

This is nice. Let’s try using it in for syntax:

scala> for {
         e1 <- "event 1 ok".right
         e2 <- "event 2 failed!".left[String]
         e3 <- "event 3 failed!".left[String]
       } yield (e1 |+| e2 |+| e3)
res24: scalaz.\/[String,String] = -\/(event 2 failed!)

As you can see, the first failure rolls up as the final result. How do we get the value out of \/? First there’s isRight and isLeft method to check which side we are on:

scala> "event 1 ok".right.isRight
res25: Boolean = true

scala> "event 1 ok".right.isLeft
res26: Boolean = false

For right side, we can use getOrElse and its symbolic alias | as follows:

scala> "event 1 ok".right | "something bad"
res27: String = event 1 ok

For left value, we can call swap method or it’s symbolic alias unary_~:

scala> ~"event 2 failed!".left[String] | "something good"
res28: String = event 2 failed!

We can use map to modify the right side value:

scala> "event 1 ok".right map {_ + "!"}
res31: scalaz.\/[Nothing,String] = \/-(event 1 ok!)

To chain on the left side, there’s orElse, which accepts => AA \/ BB where [AA >: A, BB >: B]. The symbolic alias for orElse is |||:

scala> "event 1 failed!".left ||| "retry event 1 ok".right
res32: scalaz.\/[String,String] = \/-(retry event 1 ok)

Validation 

Another data structure that’s compared to Either in Scalaz is Validation:

sealed trait Validation[+E, +A] {
  /** Return `true` if this validation is success. */
  def isSuccess: Boolean = this match {
    case Success(_) => true
    case Failure(_) => false
  }
  /** Return `true` if this validation is failure. */
  def isFailure: Boolean = !isSuccess

  ...
}

final case class Success[E, A](a: A) extends Validation[E, A]
final case class Failure[E, A](e: E) extends Validation[E, A]

At the first glance Validation looks similar to \/. They can even be converted back and forth using validation method and disjunction method.

ValidationOps introduces success[X], successNel[X], failure[X], and failureNel[X] methods to all data types (don’t worry about the Nel thing for now):

scala> "event 1 ok".success[String]
res36: scalaz.Validation[String,String] = Success(event 1 ok)

scala> "event 1 failed!".failure[String]
res38: scalaz.Validation[String,String] = Failure(event 1 failed!)

What’s different about Validation is that it is not a monad, but it’s an applicative functor. Instead of chaining the result from first event to the next, Validation validates all events:

scala> ("event 1 ok".success[String] |@| "event 2 failed!".failure[String] |@| "event 3 failed!".failure[String]) {_ + _ + _}
res44: scalaz.Unapply[scalaz.Apply,scalaz.Validation[String,String]]{type M[X] = scalaz.Validation[String,X]; type A = String}#M[String] = Failure(event 2 failed!event 3 failed!)

It’s a bit difficult to see, but the final result is Failure(event 2 failed!event 3 failed!). Unlike \/ monad which cut the calculation short, Validation keeps going and reports back all failures. This probably would be useful for validating user’s input on an online bacon shop.

The problem, however, is that the error messages are mushed together into one string. Shouldn’t it be something like a list?

NonEmptyList 

This is where NonEmptyList (or Nel for short) comes in:

/** A singly-linked list that is guaranteed to be non-empty. */
sealed trait NonEmptyList[+A] {
  val head: A
  val tail: List[A]
  def <::[AA >: A](b: AA): NonEmptyList[AA] = nel(b, head :: tail)
  ...
}

This is a wrapper trait for plain List that’s guaranteed to be non-empty. Since there’s at least one item in the list, head always works. IdOps adds wrapNel to all data types to create a Nel.

scala> 1.wrapNel
res47: scalaz.NonEmptyList[Int] = NonEmptyList(1)

Now does successNel[X] and failureNel[X] make sense?

scala> "event 1 ok".successNel[String]
res48: scalaz.ValidationNEL[String,String] = Success(event 1 ok)

scala> "event 1 failed!".failureNel[String]
res49: scalaz.ValidationNEL[String,String] = Failure(NonEmptyList(event 1 failed!))

scala> ("event 1 ok".successNel[String] |@| "event 2 failed!".failureNel[String] |@| "event 3 failed!".failureNel[String]) {_ + _ + _}
res50: scalaz.Unapply[scalaz.Apply,scalaz.ValidationNEL[String,String]]{type M[X] = scalaz.ValidationNEL[String,X]; type A = String}#M[String] = Failure(NonEmptyList(event 2 failed!, event 3 failed!))

In Failure, we were able to accumulate all failed messages.

We will pick it up from here later.

day 8 

On day 7 we reviewed Applicative Builder, and looked at State monad, \/ monad, and Validation. Let’s continue on.

Some useful monadic functions 

Learn You a Haskell for Great Good says:

In this section, we’re going to explore a few functions that either operate on monadic values or return monadic values as their results (or both!). Such functions are usually referred to as monadic functions.

In Scalaz Monad extends Applicative, so there’s no question that all monads are functors. This means we can use map or <*> operator.

join method 

LYAHFGG:

It turns out that any nested monadic value can be flattened and that this is actually a property unique to monads. For this, the join function exists.

In Scalaz join (and its symbolic alias μ) is a method introduced by Bind:

trait BindOps[F[_],A] extends Ops[F[A]] {
  ...
  def join[B](implicit ev: A <~< F[B]): F[B] = F.bind(self)(ev(_))
  def μ[B](implicit ev: A <~< F[B]): F[B] = F.bind(self)(ev(_))
  ...
}

Let’s try it out:

scala> (Some(9.some): Option[Option[Int]]).join
res9: Option[Int] = Some(9)

scala> (Some(none): Option[Option[Int]]).join
res10: Option[Int] = None

scala> List(List(1, 2, 3), List(4, 5, 6)).join
res12: List[Int] = List(1, 2, 3, 4, 5, 6)

scala> 9.right[String].right[String].join
res15: scalaz.Unapply[scalaz.Bind,scalaz.\/[String,scalaz.\/[String,Int]]]{type M[X] = scalaz.\/[String,X]; type A = scalaz.\/[String,Int]}#M[Int] = \/-(9)

scala> "boom".left[Int].right[String].join
res16: scalaz.Unapply[scalaz.Bind,scalaz.\/[String,scalaz.\/[String,Int]]]{type M[X] = scalaz.\/[String,X]; type A = scalaz.\/[String,Int]}#M[Int] = -\/(boom)

filterM method 

LYAHFGG:

The filterM function from Control.Monad does just what we want! … The predicate returns a monadic value whose result is a Bool.

In Scalaz filterM is implemented in several places.

trait ListOps[A] extends Ops[List[A]] {
  ...
  final def filterM[M[_] : Monad](p: A => M[Boolean]): M[List[A]] = l.filterM(self)(p)
  ...
}

scala> List(1, 2, 3) filterM { x => List(true, false) }
res19: List[List[Int]] = List(List(1, 2, 3), List(1, 2), List(1, 3), List(1), List(2, 3), List(2), List(3), List())

scala> Vector(1, 2, 3) filterM { x => Vector(true, false) }
res20: scala.collection.immutable.Vector[Vector[Int]] = Vector(Vector(1, 2, 3), Vector(1, 2), Vector(1, 3), Vector(1), Vector(2, 3), Vector(2), Vector(3), Vector())

foldLeftM method 

LYAHFGG:

The monadic counterpart to foldl is foldM.

In Scalaz, this is implemented in Foldable as foldLeftM. There’s also foldRightM too.

scala> def binSmalls(acc: Int, x: Int): Option[Int] = {
         if (x > 9) (none: Option[Int])
         else (acc + x).some
       }
binSmalls: (acc: Int, x: Int)Option[Int]

scala> List(2, 8, 3, 1).foldLeftM(0) {binSmalls}
res25: Option[Int] = Some(14)

scala> List(2, 11, 3, 1).foldLeftM(0) {binSmalls}
res26: Option[Int] = None

Making a safe RPN calculator 

LYAHFGG:

When we were solving the problem of implementing a RPN calculator, we noted that it worked fine as long as the input that it got made sense.

I did not cover that chapter, but the code is here so let’s translate it into Scala:

scala> def foldingFunction(list: List[Double], next: String): List[Double] = (list, next) match {
         case (x :: y :: ys, "*") => (y * x) :: ys
         case (x :: y :: ys, "+") => (y + x) :: ys
         case (x :: y :: ys, "-") => (y - x) :: ys
         case (xs, numString) => numString.toInt :: xs
       }
foldingFunction: (list: List[Double], next: String)List[Double]

scala> def solveRPN(s: String): Double =
         (s.split(' ').toList.foldLeft(Nil: List[Double]) {foldingFunction}).head
solveRPN: (s: String)Double

scala> solveRPN("10 4 3 + 2 * -")
res27: Double = -4.0

Looks like it’s working. The next step is to change the folding function to handle errors gracefully. Scalaz adds parseInt to String which returns Validation[NumberFormatException, Int]. We can call toOption on a validation to turn it into Option[Int] like the book:

scala> "1".parseInt.toOption
res31: Option[Int] = Some(1)

scala> "foo".parseInt.toOption
res32: Option[Int] = None

Here’s the updated folding function:

scala> def foldingFunction(list: List[Double], next: String): Option[List[Double]] = (list, next) match {
         case (x :: y :: ys, "*") => ((y * x) :: ys).point[Option]
         case (x :: y :: ys, "+") => ((y + x) :: ys).point[Option]
         case (x :: y :: ys, "-") => ((y - x) :: ys).point[Option]
         case (xs, numString) => numString.parseInt.toOption map {_ :: xs}
       }
foldingFunction: (list: List[Double], next: String)Option[List[Double]]

scala> foldingFunction(List(3, 2), "*")
res33: Option[List[Double]] = Some(List(6.0))

scala> foldingFunction(Nil, "*")
res34: Option[List[Double]] = None

scala> foldingFunction(Nil, "wawa")
res35: Option[List[Double]] = None

Here’s the updated solveRPN:

scala> def solveRPN(s: String): Option[Double] = for {
         List(x) <- s.split(' ').toList.foldLeftM(Nil: List[Double]) {foldingFunction}
       } yield x
solveRPN: (s: String)Option[Double]

scala> solveRPN("1 2 * 4 +")
res36: Option[Double] = Some(6.0)

scala> solveRPN("1 2 * 4")
res37: Option[Double] = None

scala> solveRPN("1 8 garbage")
res38: Option[Double] = None

Composing monadic functions 

LYAHFGG:

When we were learning about the monad laws, we said that the <=< function is just like composition, only instead of working for normal functions like a -> b, it works for monadic functions like a -> m b.

Looks like I missed this one too.

Kleisli 

In Scalaz there’s a special wrapper for function of type A => M[B] called Kleisli:

sealed trait Kleisli[M[+_], -A, +B] { self =>
  def run(a: A): M[B]
  ...
  /** alias for `andThen` */
  def >=>[C](k: Kleisli[M, B, C])(implicit b: Bind[M]): Kleisli[M, A, C] =  kleisli((a: A) => b.bind(this(a))(k(_)))
  def andThen[C](k: Kleisli[M, B, C])(implicit b: Bind[M]): Kleisli[M, A, C] = this >=> k
  /** alias for `compose` */
  def <=<[C](k: Kleisli[M, C, A])(implicit b: Bind[M]): Kleisli[M, C, B] = k >=> this
  def compose[C](k: Kleisli[M, C, A])(implicit b: Bind[M]): Kleisli[M, C, B] = k >=> this
  ...
}

object Kleisli extends KleisliFunctions with KleisliInstances {
  def apply[M[+_], A, B](f: A => M[B]): Kleisli[M, A, B] = kleisli(f)
}

We can use Kleisli object to construct it:

scala> val f = Kleisli { (x: Int) => (x + 1).some }
f: scalaz.Kleisli[Option,Int,Int] = scalaz.KleisliFunctions$$anon$18@7da2734e

scala> val g = Kleisli { (x: Int) => (x * 100).some }
g: scalaz.Kleisli[Option,Int,Int] = scalaz.KleisliFunctions$$anon$18@49e07991

We can then compose the functions using <=<, which runs rhs first like f compose g:

scala> 4.some >>= (f <=< g)
res59: Option[Int] = Some(401)

There’s also >=>, which runs lhs first like f andThen g:

scala> 4.some >>= (f >=> g)
res60: Option[Int] = Some(500)

Reader again 

As a bonus, Scalaz defines Reader as a special case of Kleisli as follows:

  type ReaderT[F[+_], E, A] = Kleisli[F, E, A]
  type Reader[E, A] = ReaderT[Id, E, A]
  object Reader {
    def apply[E, A](f: E => A): Reader[E, A] = Kleisli[Id, E, A](f)
  }

We can rewrite the reader example from day 6 as follows:

scala> val addStuff: Reader[Int, Int] = for {
         a <- Reader { (_: Int) * 2 }
         b <- Reader { (_: Int) + 10 }
       } yield a + b
addStuff: scalaz.Reader[Int,Int] = scalaz.KleisliFunctions$$anon$18@343bd3ae

scala> addStuff(3)
res76: scalaz.Id.Id[Int] = 19

The fact that we are using function as a monad becomes somewhat clearer here.

Making monads 

LYAHFGG:

In this section, we’re going to look at an example of how a type gets made, identified as a monad and then given the appropriate Monad instance. … What if we wanted to model a non-deterministic value like [3,5,9], but we wanted to express that 3 has a 50% chance of happening and 5 and 9 both have a 25% chance of happening?

Since Scala doesn’t have a built-in rational, let’s just use Double. Here’s the case class:

scala> :paste
// Entering paste mode (ctrl-D to finish)

case class Prob[A](list: List[(A, Double)])

trait ProbInstances {
  implicit def probShow[A]: Show[Prob[A]] = Show.showA
}

case object Prob extends ProbInstances

// Exiting paste mode, now interpreting.

defined class Prob
defined trait ProbInstances
defined module Prob

Is this a functor? Well, the list is a functor, so this should probably be a functor as well, because we just added some stuff to the list.

scala> :paste
// Entering paste mode (ctrl-D to finish)

case class Prob[A](list: List[(A, Double)])

trait ProbInstances {
  implicit val probInstance = new Functor[Prob] {
    def map[A, B](fa: Prob[A])(f: A => B): Prob[B] =
      Prob(fa.list map { case (x, p) => (f(x), p) })
  }
  implicit def probShow[A]: Show[Prob[A]] = Show.showA
}

case object Prob extends ProbInstances

scala> Prob((3, 0.5) :: (5, 0.25) :: (9, 0.25) :: Nil) map {-_} 
res77: Prob[Int] = Prob(List((-3,0.5), (-5,0.25), (-9,0.25)))

Just like the book we are going to implement flatten first.

case class Prob[A](list: List[(A, Double)])

trait ProbInstances {
  def flatten[B](xs: Prob[Prob[B]]): Prob[B] = {
    def multall(innerxs: Prob[B], p: Double) =
      innerxs.list map { case (x, r) => (x, p * r) }
    Prob((xs.list map { case (innerxs, p) => multall(innerxs, p) }).flatten)
  }

  implicit val probInstance = new Functor[Prob] {
    def map[A, B](fa: Prob[A])(f: A => B): Prob[B] =
      Prob(fa.list map { case (x, p) => (f(x), p) })
  }
  implicit def probShow[A]: Show[Prob[A]] = Show.showA
}

case object Prob extends ProbInstances

This should be enough prep work for monad:

scala> :paste
// Entering paste mode (ctrl-D to finish)

case class Prob[A](list: List[(A, Double)])

trait ProbInstances {
  def flatten[B](xs: Prob[Prob[B]]): Prob[B] = {
    def multall(innerxs: Prob[B], p: Double) =
      innerxs.list map { case (x, r) => (x, p * r) }
    Prob((xs.list map { case (innerxs, p) => multall(innerxs, p) }).flatten)
  }

  implicit val probInstance = new Functor[Prob] with Monad[Prob] {
    def point[A](a: => A): Prob[A] = Prob((a, 1.0) :: Nil)
    def bind[A, B](fa: Prob[A])(f: A => Prob[B]): Prob[B] = flatten(map(fa)(f)) 
    override def map[A, B](fa: Prob[A])(f: A => B): Prob[B] =
      Prob(fa.list map { case (x, p) => (f(x), p) })
  }
  implicit def probShow[A]: Show[Prob[A]] = Show.showA
}

case object Prob extends ProbInstances

// Exiting paste mode, now interpreting.

defined class Prob
defined trait ProbInstances
defined module Prob

The book says it satisfies the monad laws. Let’s implement the Coin example:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait Coin
case object Heads extends Coin
case object Tails extends Coin
implicit val coinEqual: Equal[Coin] = Equal.equalA

def coin: Prob[Coin] = Prob(Heads -> 0.5 :: Tails -> 0.5 :: Nil)
def loadedCoin: Prob[Coin] = Prob(Heads -> 0.1 :: Tails -> 0.9 :: Nil)

def flipThree: Prob[Boolean] = for {
  a <- coin
  b <- coin
  c <- loadedCoin
} yield { List(a, b, c) all {_ === Tails} }

// Exiting paste mode, now interpreting.

defined trait Coin
defined module Heads
defined module Tails
coin: Prob[Coin]
loadedCoin: Prob[Coin]
flipThree: Prob[Boolean]

scala> flipThree
res81: Prob[Boolean] = Prob(List((false,0.025), (false,0.225), (false,0.025), (false,0.225), (false,0.025), (false,0.225), (false,0.025), (true,0.225)))

So the probability of having all three coins on Tails even with a loaded coin is pretty low.

We will continue from here later.

day 9 

On day 8 we reviewed monadic functions join, filterM, and foldLeftM, implemented safe RPN calculator, looked at Kleisli to compose monadic functions, and implemented our own monad Prob.

Anyway, let’s see some of the typeclasses that we didn’t have opportunity to cover.

Tree 

Let’s start the final chapter of Learn You a Haskell for Great Good: Zippers:

In this chapter, we’ll see how we can take some data structure and focus on a part of it in a way that makes changing its elements easy and walking around it efficient.

I can see how this could be useful in Scala since equality of case classes are based on its content and not the heap location. This means that even if you just want to identify different nodes under a tree structure if they happen to have the same type and content Scala would treat the same.

Instead of implementing our own tree, let’s use Scalaz’s Tree:

sealed trait Tree[A] {
  /** The label at the root of this tree. */
  def rootLabel: A
  /** The child nodes of this tree. */
  def subForest: Stream[Tree[A]]
}

object Tree extends TreeFunctions with TreeInstances {
  /** Construct a tree node with no children. */
  def apply[A](root: => A): Tree[A] = leaf(root)

  object Node {
    def unapply[A](t: Tree[A]): Option[(A, Stream[Tree[A]])] = Some((t.rootLabel, t.subForest))
  }
}

trait TreeFunctions {
  /** Construct a new Tree node. */
  def node[A](root: => A, forest: => Stream[Tree[A]]): Tree[A] = new Tree[A] {
    lazy val rootLabel = root
    lazy val subForest = forest
    override def toString = "<tree>"
  }
  /** Construct a tree node with no children. */
  def leaf[A](root: => A): Tree[A] = node(root, Stream.empty)
  ...
}

This is a multi-way tree. To create a tree use node and leaf methods injected to all data types:

trait TreeV[A] extends Ops[A] {
  def node(subForest: Tree[A]*): Tree[A] = Tree.node(self, subForest.toStream)

  def leaf: Tree[A] = Tree.leaf(self)
}

Let’s implement freeTree from the book using this:

scala> def freeTree: Tree[Char] =
         'P'.node(
           'O'.node(
             'L'.node('N'.leaf, 'T'.leaf),
             'Y'.node('S'.leaf, 'A'.leaf)),
           'L'.node(
             'W'.node('C'.leaf, 'R'.leaf),
             'A'.node('A'.leaf, 'C'.leaf)))
freeTree: scalaz.Tree[Char]

LYAHFGG:

Notice that W in the tree there? Say we want to change it into a P.

Using Tree.Node extractor, we could implement changeToP as follows:

scala> def changeToP(tree: Tree[Char]): Tree[Char] = tree match {
         case Tree.Node(x, Stream(
           l, Tree.Node(y, Stream(
             Tree.Node(_, Stream(m, n)), r)))) =>
           x.node(l, y.node('P'.node(m, n), r))
       }
changeToP: (tree: scalaz.Tree[Char])scalaz.Tree[Char]

This was a pain to implement. Let’s look at the zipper.

TreeLoc 

LYAHFGG:

With a pair of Tree a and Breadcrumbs a, we have all the information to rebuild the whole tree and we also have a focus on a sub-tree. This scheme also enables us to easily move up, left and right. Such a pair that contains a focused part of a data structure and its surroundings is called a zipper, because moving our focus up and down the data structure resembles the operation of a zipper on a regular pair of pants.

The zipper for Tree in Scalaz is called TreeLoc:

sealed trait TreeLoc[A] {
  import TreeLoc._
  import Tree._

  /** The currently selected node. */
  val tree: Tree[A]
  /** The left siblings of the current node. */
  val lefts: TreeForest[A]
  /** The right siblings of the current node. */
  val rights: TreeForest[A]
  /** The parent contexts of the current node. */
  val parents: Parents[A]
  ...
}

object TreeLoc extends TreeLocFunctions with TreeLocInstances {
  def apply[A](t: Tree[A], l: TreeForest[A], r: TreeForest[A], p: Parents[A]): TreeLoc[A] =
    loc(t, l, r, p)
}

trait TreeLocFunctions {
  type TreeForest[A] = Stream[Tree[A]]
  type Parent[A] = (TreeForest[A], A, TreeForest[A])
  type Parents[A] = Stream[Parent[A]]
}

A zipper data structure represents a hole. We have the current focus represented as tree, but everything else that can construct the entire tree back up is also preserved. To create TreeLoc call loc method on a Tree:

scala> freeTree.loc
res0: scalaz.TreeLoc[Char] = scalaz.TreeLocFunctions$$anon$2@6439ca7b

TreeLoc implements various methods to move the focus around, similar to DOM API:

sealed trait TreeLoc[A] {
  ...
  /** Select the parent of the current node. */
  def parent: Option[TreeLoc[A]] = ...
  /** Select the root node of the tree. */
  def root: TreeLoc[A] = ...
  /** Select the left sibling of the current node. */
  def left: Option[TreeLoc[A]] = ...
  /** Select the right sibling of the current node. */
  def right: Option[TreeLoc[A]] = ...
  /** Select the leftmost child of the current node. */
  def firstChild: Option[TreeLoc[A]] = ...
  /** Select the rightmost child of the current node. */
  def lastChild: Option[TreeLoc[A]] = ...
  /** Select the nth child of the current node. */
  def getChild(n: Int): Option[TreeLoc[A]] = ...
  /** Select the first immediate child of the current node that satisfies the given predicate. */
  def findChild(p: Tree[A] => Boolean): Option[TreeLoc[A]] = ...
  /** Get the label of the current node. */
  def getLabel: A = ...
  ...
}

To move focus to W of freeTree, we can write something like:

scala> freeTree.loc.getChild(2) >>= {_.getChild(1)}
res8: Option[scalaz.TreeLoc[Char]] = Some(scalaz.TreeLocFunctions$$anon$2@417ef051)

scala> freeTree.loc.getChild(2) >>= {_.getChild(1)} >>= {_.getLabel.some}
res9: Option[Char] = Some(W)

Note getChild returns an Option[TreeLoc[A]] so we need to use monadic chaining >>=, which is the same as flatMap. The odd thing is that getChild uses 1-based index! There are various methods to create a new TreeLoc with modification, but useful looking ones are:

  /** Modify the current node with the given function. */
  def modifyTree(f: Tree[A] => Tree[A]): TreeLoc[A] = ...
  /** Modify the label at the current node with the given function. */
  def modifyLabel(f: A => A): TreeLoc[A] = ...
  /** Insert the given node as the last child of the current node and give it focus. */
  def insertDownLast(t: Tree[A]): TreeLoc[A] = ...

So let’s modify the label to 'P':

scala> val newFocus = freeTree.loc.getChild(2) >>= {_.getChild(1)} >>= {_.modifyLabel({_ => 'P'}).some}
newFocus: Option[scalaz.TreeLoc[Char]] = Some(scalaz.TreeLocFunctions$$anon$2@107a26d0)

To reconstruct a new tree from newFocus we just call toTree method:

scala> newFocus.get.toTree
res19: scalaz.Tree[Char] = <tree>

scala> newFocus.get.toTree.draw foreach {_.print}
P|O+- ||  L+- |  ||  |  N+- |  |  ||  |  T`- |  |  ||  Y`- |  |   |  S+-    |  |   |  A`-    |  |L`- |   P+-    ||     C+- |     ||     R`- |     |   A`-    |      A+-       |      C`-

To see check what’s inside the tree there’s draw method on Tree, but it looks odd printed with or without newline.

Zipper 

LYAHFGG:

Zippers can be used with pretty much any data structure, so it’s no surprise that they can be used to focus on sub-lists of lists.

Instead of a list zipper, Scalaz provides a zipper for Stream. Due to Haskell’s laziness, it might actually make sense to think of Scala’s Stream as Haskell’s list. Here’s Zipper:

sealed trait Zipper[+A] {
  val focus: A
  val lefts: Stream[A]
  val rights: Stream[A]
  ...
}

To create a zipper use toZipper or zipperEnd method injected to Stream:

trait StreamOps[A] extends Ops[Stream[A]] {
  final def toZipper: Option[Zipper[A]] = s.toZipper(self)
  final def zipperEnd: Option[Zipper[A]] = s.zipperEnd(self)
  ...
}

Let’s try using it.

scala> Stream(1, 2, 3, 4)
res23: scala.collection.immutable.Stream[Int] = Stream(1, ?)

scala> Stream(1, 2, 3, 4).toZipper
res24: Option[scalaz.Zipper[Int]] = Some(Zipper(<lefts>, 1, <rights>))

As with TreeLoc there are lots of methods on Zipper to move around:

sealed trait Zipper[+A] {
  ...
  /** Possibly moves to next element to the right of focus. */
  def next: Option[Zipper[A]] = ...
  def nextOr[AA >: A](z: => Zipper[AA]): Zipper[AA] = next getOrElse z
  def tryNext: Zipper[A] = nextOr(sys.error("cannot move to next element"))
  /** Possibly moves to the previous element to the left of focus. */
  def previous: Option[Zipper[A]] = ...
  def previousOr[AA >: A](z: => Zipper[AA]): Zipper[AA] = previous getOrElse z
  def tryPrevious: Zipper[A] = previousOr(sys.error("cannot move to previous element"))
  /** Moves focus n elements in the zipper, or None if there is no such element. */
  def move(n: Int): Option[Zipper[A]] = ...
  def findNext(p: A => Boolean): Option[Zipper[A]] = ...
  def findPrevious(p: A => Boolean): Option[Zipper[A]] = ...

  def modify[AA >: A](f: A => AA) = ...
  def toStream: Stream[A] = ...
  ...
}

Here are these functions in action:

scala> Stream(1, 2, 3, 4).toZipper >>= {_.next}
res25: Option[scalaz.Zipper[Int]] = Some(Zipper(<lefts>, 2, <rights>))

scala> Stream(1, 2, 3, 4).toZipper >>= {_.next} >>= {_.next}
res26: Option[scalaz.Zipper[Int]] = Some(Zipper(<lefts>, 3, <rights>))

scala> Stream(1, 2, 3, 4).toZipper >>= {_.next} >>= {_.next} >>= {_.previous}
res27: Option[scalaz.Zipper[Int]] = Some(Zipper(<lefts>, 2, <rights>))

To modify the current focus and bring it back to a Stream, use modify and toStream method:

scala> Stream(1, 2, 3, 4).toZipper >>= {_.next} >>= {_.next} >>= {_.modify {_ => 7}.some}
res31: Option[scalaz.Zipper[Int]] = Some(Zipper(<lefts>, 7, <rights>))

scala> res31.get.toStream.toList
res32: List[Int] = List(1, 2, 7, 4)

We can also write this using for syntax:

scala> for {
         z <- Stream(1, 2, 3, 4).toZipper
         n1 <- z.next
         n2 <- n1.next
       } yield { n2.modify {_ => 7} }
res33: Option[scalaz.Zipper[Int]] = Some(Zipper(<lefts>, 7, <rights>))

More readable, I guess, but it does take up lines so it’s case by case.

This is pretty much the end of Learn You a Haskell for Great Good. It did not cover everything Scalaz has to offer, but I think it was an exellent way of gently getting introduced to the fundamentals. After looking up the corresponding Scalaz types for Haskell types, I am now comfortable enough to find my way around the source code and look things up as I go.

Id 

Using Hoogle we can look up Haskell typeclasses. For example, let’s look at Control.Monad.Identity:

The Identity monad is a monad that does not embody any computational strategy. It simply applies the bound function to its input without any modification. Computationally, there is no reason to use the Identity monad instead of the much simpler act of simply applying functions to their arguments. The purpose of the Identity monad is its fundamental role in the theory of monad transformers. Any monad transformer applied to the Identity monad yields a non-transformer version of that monad.

Here’s the corresponding type in Scalaz:

  /** The strict identity type constructor. Can be thought of as `Tuple1`, but with no
   *  runtime representation.
   */
  type Id[+X] = X

We need to look at monad transformer later, but one thing that’s interesting is that all data types can be Id of the type.

scala> (0: Id[Int])
res39: scalaz.Scalaz.Id[Int] = 0

Scalaz introduces several useful methods via Id:

trait IdOps[A] extends Ops[A] {
  /**Returns `self` if it is non-null, otherwise returns `d`. */
  final def ??(d: => A)(implicit ev: Null <:< A): A =
    if (self == null) d else self
  /**Applies `self` to the provided function */
  final def |>[B](f: A => B): B = f(self)
  final def squared: (A, A) = (self, self)
  def left[B]: (A \/ B) = \/.left(self)
  def right[B]: (B \/ A) = \/.right(self)
  final def wrapNel: NonEmptyList[A] = NonEmptyList(self)
  /** @return the result of pf(value) if defined, otherwise the the Zero element of type B. */
  def matchOrZero[B: Monoid](pf: PartialFunction[A, B]): B = ...
  /** Repeatedly apply `f`, seeded with `self`, checking after each iteration whether the predicate `p` holds. */
  final def doWhile(f: A => A, p: A => Boolean): A = ...
  /** Repeatedly apply `f`, seeded with `self`, checking before each iteration whether the predicate `p` holds. */
  final def whileDo(f: A => A, p: A => Boolean): A = ...
  /** If the provided partial function is defined for `self` run this,
   * otherwise lift `self` into `F` with the provided [[scalaz.Pointed]]. */
  def visit[F[_] : Pointed](p: PartialFunction[A, F[A]]): F[A] = ...
}

|> lets you write the function application at the end of an expression:

scala> 1 + 2 + 3 |> {_.point[List]}
res45: List[Int] = List(6)

scala> 1 + 2 + 3 |> {_ * 6}
res46: Int = 36

visit is also kind of interesting:

scala> 1 visit { case x@(2|3) => List(x * 2) }
res55: List[Int] = List(1)

scala> 2 visit { case x@(2|3) => List(x * 2) }
res56: List[Int] = List(4)

Lawless typeclasses 

Scalaz 7.0 contains several typeclasses that are now deemed lawless by Scalaz project: Length, Index, and Each. Some discussions can be found in #278 What to do about lawless classes? and (presumably) Bug in IndexedSeq Index typeclass. The three will be deprecated in 7.1, and removed in 7.2.

Length 

There’s a typeclass that expresses length. Here’s the typeclass contract of Length:

trait Length[F[_]]  { self =>
  def length[A](fa: F[A]): Int
}

This introduces length method. In Scala standard library it’s introduced by SeqLike, so it could become useful if there were data structure that does not extend SeqLike that has length.

Index 

For random access into a container, there’s Index:

trait Index[F[_]]  { self =>
  def index[A](fa: F[A], i: Int): Option[A]
}

This introduces index and indexOr methods:

trait IndexOps[F[_],A] extends Ops[F[A]] {
  final def index(n: Int): Option[A] = F.index(self, n)
  final def indexOr(default: => A, n: Int): A = F.indexOr(self, default, n)
}

This is similar to List(n) except it returns None for an out-of-range index:

scala> List(1, 2, 3)(3)
java.lang.IndexOutOfBoundsException: 3
        ...

scala> List(1, 2, 3) index 3
res62: Option[Int] = None

Each 

For running side effects along a data structure, there’s Each:

trait Each[F[_]]  { self =>
  def each[A](fa: F[A])(f: A => Unit)
}

This introduces foreach method:

sealed abstract class EachOps[F[_],A] extends Ops[F[A]] {
  final def foreach(f: A => Unit): Unit = F.each(self)(f)
}

Foldable or rolling your own? 

Some of the functionality above can be emulated using Foldable, but as @nuttycom suggested, that would force O(n) time even when the underlying data structure implements constant time for length and index. At that point, we’d be better off rolling our own Length if it’s actually useful to abstract over length.

If inconsistent implementations of these typeclasses were somehow compromising the typesafety I’d understand removing them from the library, but Length and Index sound like a legitimate abstraction of randomly accessible containers like Vector.

Pointed and Copointed 

There actually was another set of typeclasses that was axed earlier: Pointed and Copointed. There were more interesting arguments on them that can be found in Pointed/Copointed and Why not Pointed?:

Pointed has no useful laws and almost all applications people point to for it are actually abuses of ad hoc relationships it happens to have for the instances it does offer.

This actually is an interesting line of argument that I can understand. In other words, if any container can qualify as Pointed, the code using it either is not very useful or it’s likely making specific assumption about the instance.

Tweets to the editor 

@eed3si9n "axiomatic" would be better.

— Miles Sabin (@milessabin) December 29, 2013

@eed3si9n Foldable too (unless it also has a Functor but then nothing past parametricity): https://t.co/Lp0YkUTRD9 - but Reducer has laws!

— Brian McKenna (@puffnfresh) December 29, 2013

day 10 

On day 9 we looked at how to update immutable data structure using TreeLoc for Trees and Zipper for Streams. We also picked up a few typeclasses like Id, Index and Length. Now that we are done with Learn You a Haskell for Great Good, we need to find our own topic.

One concept that I see many times in Scalaz 7 is the monad transformer, so let’s find what that’s all about. Luckily there’s another good Haskell book that I’ve read that’s also available online.

Monad transformers 

Real World Haskell says:

It would be ideal if we could somehow take the standard State monad and add failure handling to it, without resorting to the wholesale construction of custom monads by hand. The standard monads in the mtl library don’t allow us to combine them. Instead, the library provides a set of monad transformers to achieve the same result.

A monad transformer is similar to a regular monad, but it’s not a standalone entity: instead, it modifies the behaviour of an underlying monad.

Reader, yet again 

Let’s translate the Reader monad example into Scala:

scala> def myName(step: String): Reader[String, String] = Reader {step + ", I am " + _}
myName: (step: String)scalaz.Reader[String,String]

scala> def localExample: Reader[String, (String, String, String)] = for {
         a <- myName("First")
         b <- myName("Second") >=> Reader { _ + "dy"}
         c <- myName("Third")  
       } yield (a, b, c)
localExample: scalaz.Reader[String,(String, String, String)]

scala> localExample("Fred")
res0: (String, String, String) = (First, I am Fred,Second, I am Freddy,Third, I am Fred)

The point of Reader monad is to pass in the configuration information once and everyone uses it without explicitly passing it around. See Configuration Without the Bugs and Gymnastics by Tony Morris (@dibblego).

ReaderT 

Here’s an example of stacking ReaderT, monad transformer version of Reader on Option monad.

scala> :paste
// Entering paste mode (ctrl-D to finish)

type ReaderTOption[A, B] = ReaderT[Option, A, B]
object ReaderTOption extends KleisliInstances with KleisliFunctions {
  def apply[A, B](f: A => Option[B]): ReaderTOption[A, B] = kleisli(f)
}

// Exiting paste mode, now interpreting.

Now using ReaderTOption object, we can create a ReaderTOption:

scala> def configure(key: String) = ReaderTOption[Map[String, String], String] {_.get(key)}
configure: (key: String)ReaderTOption[Map[String,String],String]

On day 2 we mentioned about considering Function1 as an infinite map. Here we are doing sort of the opposite by using Map[String, String] as a reader.

scala> def setupConnection = for {
         host <- configure("host")
         user <- configure("user")
         password <- configure("password")
       } yield (host, user, password)
setupConnection: scalaz.Kleisli[Option,Map[String,String],(String, String, String)]

scala> val goodConfig = Map(
         "host" -> "eed3si9n.com",
         "user" -> "sa",
         "password" -> "****"
       )
goodConfig: scala.collection.immutable.Map[String,String] = Map(host -> eed3si9n.com, user -> sa, password -> ****)

scala> setupConnection(goodConfig)
res2: Option[(String, String, String)] = Some((eed3si9n.com,sa,****))

scala> val badConfig = Map(
         "host" -> "example.com",
         "user" -> "sa"
       )
badConfig: scala.collection.immutable.Map[String,String] = Map(host -> example.com, user -> sa)

scala> setupConnection(badConfig)
res3: Option[(String, String, String)] = None

As you can see the above ReaderTOption monad combines Reader’s ability to read from some configuration once, and Option’s ability to express failure.

Stacking multiple monad transformers 

RWH:

When we stack a monad transformer on a normal monad, the result is another monad. This suggests the possibility that we can again stack a monad transformer on top of our combined monad, to give a new monad, and in fact this is a common thing to do.

We can stack StateT to represent state transfer on top of ReaderTOption.

scala> :paste
// Entering paste mode (ctrl-D to finish)

type StateTReaderTOption[C, S, A] = StateT[({type l[X] = ReaderTOption[C, X]})#l, S, A]

object StateTReaderTOption extends StateTInstances with StateTFunctions {
  def apply[C, S, A](f: S => (S, A)) = new StateT[({type l[X] = ReaderTOption[C, X]})#l, S, A] {
    def apply(s: S) = f(s).point[({type l[X] = ReaderTOption[C, X]})#l]
  }
  def get[C, S]: StateTReaderTOption[C, S, S] =
    StateTReaderTOption { s => (s, s) }
  def put[C, S](s: S): StateTReaderTOption[C, S, Unit] =
    StateTReaderTOption { _ => (s, ()) }
}

// Exiting paste mode, now interpreting.

This is a bit confusing. Ultimately the point of State monad is to wrap S => (S, A), so I kept those parameter names. Next, we need to modify the kind of ReaderTOption to * -> * (a type constructor that takes exactly one type as its parameter).

Suppose we want to implement Stack using state like we did in day 7.

scala> type Stack = List[Int]
defined type alias Stack

scala> type Config = Map[String, String]
defined type alias Config

scala> val pop = StateTReaderTOption[Config, Stack, Int] {
         case x :: xs => (xs, x)
       }
pop: scalaz.StateT[[+X]scalaz.Kleisli[Option,Config,X],Stack,Int] = StateTReaderTOption$$anon$1@122313eb

Since I wrote get and put we should be able to write it using for syntax as well:

scala> val pop: StateTReaderTOption[Config, Stack, Int] = {
         import StateTReaderTOption.{get, put}
         for {
           s <- get[Config, Stack]
           val (x :: xs) = s
           _ <- put(xs)
         } yield x
       }
pop: StateTReaderTOption[Config,Stack,Int] = scalaz.StateT$$anon$7@7eb316d2

Here’s push:

scala> def push(x: Int): StateTReaderTOption[Config, Stack, Unit] = {
         import StateTReaderTOption.{get, put}
         for {
           xs <- get[Config, Stack]
           r <- put(x :: xs)
         } yield r
       }
push: (x: Int)StateTReaderTOption[Config,Stack,Unit]

We can also port stackManip:

scala> def stackManip: StateTReaderTOption[Config, Stack, Int] = for {
         _ <- push(3)
         a <- pop
         b <- pop
       } yield(b)
stackManip: StateTReaderTOption[Config,Stack,Int]

Here’s how we run this.

scala> stackManip(List(5, 8, 2, 1))(Map())
res12: Option[(Stack, Int)] = Some((List(8, 2, 1),5))

So far we have the same feature as the State version. Let’s modify configure:

scala> def configure[S](key: String) = new StateTReaderTOption[Config, S, String] {
         def apply(s: S) = ReaderTOption[Config, (S, String)] { config: Config => config.get(key) map {(s, _)} }
       }
configure: [S](key: String)StateTReaderTOption[Config,S,String]

Using this we can now manipulate the stack using read-only configuration:

scala> def stackManip: StateTReaderTOption[Config, Stack, Unit] = for {
         x <- configure("x")
         a <- push(x.toInt)
       } yield(a)

scala> stackManip(List(5, 8, 2, 1))(Map("x" -> "7"))
res21: Option[(Stack, Unit)] = Some((List(7, 5, 8, 2, 1),()))

scala> stackManip(List(5, 8, 2, 1))(Map("y" -> "7"))
res22: Option[(Stack, Unit)] = None

Now we have StateT, ReaderT and Option working all at the same time. Maybe I am not doing it right, but setting this up defining StateTReaderTOption and configure was painful. The usage code (stackManip) looks clean so we might do these things for special occasions like Thanksgiving.

It was rough without LYAHFGG, but we will pick it up from here later.

day 11 

Yesterday we looked at Reader monad as a way of abstracting configuration, and introduced monad transformers.

Darren Hester for openphoto.net

Today, let’s look at lenses. It’s a hot topic many people are talking, and looks like it has clear use case.

Lens 

Seth Tisue (@SethTisue) gave a talk on shapeless lenses at Scalathon this year. I missed the talk, but I am going to borrow his example.

scala> case class Point(x: Double, y: Double)
defined class Point

scala> case class Color(r: Byte, g: Byte, b: Byte)
defined class Color

scala> case class Turtle(
         position: Point,
         heading: Double,
         color: Color)

scala> Turtle(Point(2.0, 3.0), 0.0,
         Color(255.toByte, 255.toByte, 255.toByte))
res0: Turtle = Turtle(Point(2.0,3.0),0.0,Color(-1,-1,-1))

Now without breaking the immutability, we want to move the turtle forward.

scala> case class Turtle(position: Point, heading: Double, color: Color) {
         def forward(dist: Double): Turtle =
           copy(position =
             position.copy(
               x = position.x + dist * math.cos(heading),
               y = position.y + dist * math.sin(heading)
           ))
       }
defined class Turtle

scala> Turtle(Point(2.0, 3.0), 0.0,
         Color(255.toByte, 255.toByte, 255.toByte))
res10: Turtle = Turtle(Point(2.0,3.0),0.0,Color(-1,-1,-1))

scala> res10.forward(10)
res11: Turtle = Turtle(Point(12.0,3.0),0.0,Color(-1,-1,-1))

To update the child data structure, we need to nest copy call. To quote from Seth’s example again:

// imperative
a.b.c.d.e += 1

// functional
a.copy(
  b = a.b.copy(
    c = a.b.c.copy(
      d = a.b.c.d.copy(
        e = a.b.c.d.e + 1
))))

The idea is to get rid of unnecessary copy calls.

Let’s look at Lens in Scalaz7:

  type Lens[A, B] = LensT[Id, A, B]

  object Lens extends LensTFunctions with LensTInstances {
    def apply[A, B](r: A => Store[B, A]): Lens[A, B] =
      lens(r)
  }

Lens is a type alias for LensT[Id, A, B] like many other typeclasses.

LensT 

LensT looks like this:

import StoreT._
import Id._

sealed trait LensT[F[+_], A, B] {
  def run(a: A): F[Store[B, A]]
  def apply(a: A): F[Store[B, A]] = run(a)
  ...
}

object LensT extends LensTFunctions with LensTInstances {
  def apply[F[+_], A, B](r: A => F[Store[B, A]]): LensT[F, A, B] =
    lensT(r)
}

trait LensTFunctions {
  import StoreT._

  def lensT[F[+_], A, B](r: A => F[Store[B, A]]): LensT[F, A, B] = new LensT[F, A, B] {
    def run(a: A): F[Store[B, A]] = r(a)
  }

  def lensgT[F[+_], A, B](set: A => F[B => A], get: A => F[B])(implicit M: Bind[F]): LensT[F, A, B] =
    lensT(a => M(set(a), get(a))(Store(_, _)))
  def lensg[A, B](set: A => B => A, get: A => B): Lens[A, B] =
    lensgT[Id, A, B](set, get)
  def lensu[A, B](set: (A, B) => A, get: A => B): Lens[A, B] =
    lensg(set.curried, get)
  ...
}

Store 

What’s a Store?

  type Store[A, B] = StoreT[Id, A, B]
  // flipped
  type |-->[A, B] = Store[B, A]
  object Store {
    def apply[A, B](f: A => B, a: A): Store[A, B] = StoreT.store(a)(f)
  }

It looks like a wrapper for setter A => B => A and getter A => B.

Using Lens 

Let’s define turtlePosition and pointX:

scala> val turtlePosition = Lens.lensu[Turtle, Point] (
         (a, value) => a.copy(position = value),
         _.position
       )
turtlePosition: scalaz.Lens[Turtle,Point] = scalaz.LensTFunctions$$anon$5@421dc8c8

scala> val pointX = Lens.lensu[Point, Double] (
         (a, value) => a.copy(x = value),
         _.x
       )
pointX: scalaz.Lens[Point,Double] = scalaz.LensTFunctions$$anon$5@30d31cf9

Next we can take advantage of a bunch of operators introduced in Lens. Similar to monadic function composition we saw in Kleisli, LensT implements compose (symbolic alias <=<), and andThen (symbolic alias >=>). I personally think >=> looks cool, so let’s use that to define turtleX:

scala> val turtleX = turtlePosition >=> pointX
turtleX: scalaz.LensT[scalaz.Id.Id,Turtle,Double] = scalaz.LensTFunctions$$anon$5@11b35365

The type makes sense since it’s going form Turtle to Double. Using get method we can get the value:

scala> val t0 = Turtle(Point(2.0, 3.0), 0.0,
                  Color(255.toByte, 255.toByte, 255.toByte))
t0: Turtle = Turtle(Point(2.0,3.0),0.0,Color(-1,-1,-1))

scala> turtleX.get(t0)
res16: scalaz.Id.Id[Double] = 2.0

Success! Setting a new value using set method should return a new Turtle:

scala> turtleX.set(t0, 5.0)
res17: scalaz.Id.Id[Turtle] = Turtle(Point(5.0,3.0),0.0,Color(-1,-1,-1))

This works too. What if I want to get the value, apply it to some function, and set using the result? mod does exactly that:

scala> turtleX.mod(_ + 1.0, t0)
res19: scalaz.Id.Id[Turtle] = Turtle(Point(3.0,3.0),0.0,Color(-1,-1,-1))

There’s a symbolic variation to mod that’s curried called =>=. This generates Turtle => Turtle function:

scala> val incX = turtleX =>= {_ + 1.0}
incX: Turtle => scalaz.Id.Id[Turtle] = <function1>

scala> incX(t0)
res26: scalaz.Id.Id[Turtle] = Turtle(Point(3.0,3.0),0.0,Color(-1,-1,-1))

We are now describing change of internal values upfront and passing in the actual value at the end. Does this remind you of something?

Lens as a State monad 

That sounds like a state transition to me. In fact Lens and State I think are good match since they are sort of emulating imperative programming on top of immutable data structure. Here’s another way of writing incX:

scala> val incX = for {
         x <- turtleX %= {_ + 1.0}
       } yield x
incX: scalaz.StateT[scalaz.Id.Id,Turtle,Double] = scalaz.StateT$$anon$7@38e61ffa

scala> incX(t0)
res28: (Turtle, Double) = (Turtle(Point(3.0,3.0),0.0,Color(-1,-1,-1)),3.0)

%= method takes a function Double => Double and returns a State monad that expresses the change.

Let’s make turtleHeading and turtleY too:

scala> val turtleHeading = Lens.lensu[Turtle, Double] (
         (a, value) => a.copy(heading = value),
         _.heading
       )
turtleHeading: scalaz.Lens[Turtle,Double] = scalaz.LensTFunctions$$anon$5@44fdec57

scala> val pointY = Lens.lensu[Point, Double] (
         (a, value) => a.copy(y = value),
         _.y
       )
pointY: scalaz.Lens[Point,Double] = scalaz.LensTFunctions$$anon$5@ddede8c

scala> val turtleY = turtlePosition >=> pointY

This is no fun because it feels boilerplatey. But, we can now move turtle forward! Instead of general %=, Scalaz even provides sugars like += for Numeric lenses. Here’s what I mean:

scala> def forward(dist: Double) = for {
         heading <- turtleHeading
         x <- turtleX += dist * math.cos(heading)
         y <- turtleY += dist * math.sin(heading)
       } yield (x, y)
forward: (dist: Double)scalaz.StateT[scalaz.Id.Id,Turtle,(Double, Double)]

scala> forward(10.0)(t0)
res31: (Turtle, (Double, Double)) = (Turtle(Point(12.0,3.0),0.0,Color(-1,-1,-1)),(12.0,3.0))

scala> forward(10.0) exec (t0)
res32: scalaz.Id.Id[Turtle] = Turtle(Point(12.0,3.0),0.0,Color(-1,-1,-1))

Now we have implemented forward function without using a single copy(position = ...). It’s nice but we still needed some prep work to get here, so there is some tradeoff. Lens defines a lot more methods, but the above should be a good starter. Let’s see them all again:

sealed trait LensT[F[+_], A, B] {
  def get(a: A)(implicit F: Functor[F]): F[B] =
    F.map(run(a))(_.pos)
  def set(a: A, b: B)(implicit F: Functor[F]): F[A] =
    F.map(run(a))(_.put(b))
  /** Modify the value viewed through the lens */
  def mod(f: B => B, a: A)(implicit F: Functor[F]): F[A] = ...
  def =>=(f: B => B)(implicit F: Functor[F]): A => F[A] =
    mod(f, _)
  /** Modify the portion of the state viewed through the lens and return its new value. */
  def %=(f: B => B)(implicit F: Functor[F]): StateT[F, A, B] =
    mods(f)
  /** Lenses can be composed */
  def compose[C](that: LensT[F, C, A])(implicit F: Bind[F]): LensT[F, C, B] = ...
  /** alias for `compose` */
  def <=<[C](that: LensT[F, C, A])(implicit F: Bind[F]): LensT[F, C, B] = compose(that)
  def andThen[C](that: LensT[F, B, C])(implicit F: Bind[F]): LensT[F, A, C] =
    that compose this
  /** alias for `andThen` */
  def >=>[C](that: LensT[F, B, C])(implicit F: Bind[F]): LensT[F, A, C] = andThen(that)
}

Lens laws 

Seth says:

lens laws are common sense

(0. if I get twice, I get the same answer) 1. if I get, then set it back, nothing changes. 2. if I set, then get, I get what I set. 3. if I set twice then get, I get the second thing I set.

He’s right. These are common sense. Here how Scalaz expresses it in code:

  trait LensLaw {
    def identity(a: A)(implicit A: Equal[A], ev: F[Store[B, A]] =:= Id[Store[B, A]]): Boolean = {
      val c = run(a)
      A.equal(c.put(c.pos), a)
    }
    def retention(a: A, b: B)(implicit B: Equal[B], ev: F[Store[B, A]] =:= Id[Store[B, A]]): Boolean =
      B.equal(run(run(a) put b).pos, b)
    def doubleSet(a: A, b1: B, b2: B)(implicit A: Equal[A], ev: F[Store[B, A]] =:= Id[Store[B, A]]) = {
      val r = run(a)
      A.equal(run(r put b1) put b2, r put b2)
    }
  }

By making arbitrary turtles we can check if our turtleX is ok. We’ll skip it, but make sure you don’t define weird lens that break the law.

Links 

There’s an article by Jordan West titled An Introduction to Lenses in Scalaz, which I kind of skimmed and looks like Scalaz 6.

There’s a video by Edward Kmett’s Lenses: A Functional Imperative presented at the Boston Area Scala Enthusiasts (BASE).

Finally, there’s a compiler plugin by Gerolf Seitz that generates lenses: gseitz/Lensed. The project seems to be at experimental stage, but it does show the potential of macro or compiler generating lenses instead of hand-coding them.

We’ll pick it up from here later.

day 12 

On day 11 we looked at Lens as a way of abstracting access to nested immutable data structure.

reynaldo f. tamayo for openphoto.net

Today, let’s skim some papers. First is Origami programming by Jeremy Gibbons.

Origami programming 

Gibbons says:

In this chapter we will look at folds and unfolds as abstractions. In a precise technical sense, folds and unfolds are the natural patterns of computation over recursive datatypes; unfolds generate data structures and folds consume them.

We’ve covered foldLeft in day 4 using Foldable, but what’s unfold?

The dual of folding is unfolding. The Haskell standard List library defines the function unfoldr for generating lists.

Hoogle lists the following sample:

Prelude Data.List> unfoldr (\b -> if b == 0 then Nothing else Just (b, b-1)) 10
[10,9,8,7,6,5,4,3,2,1]

DList 

There’s a data structure called DList that supports DList.unfoldr. DList, or difference list, is a data structure that supports constant-time appending.

scala> DList.unfoldr(10, { (x: Int) => if (x == 0) none else (x, x - 1).some })
res50: scalaz.DList[Int] = scalaz.DListFunctions$$anon$3@70627153

scala> res50.toList
res51: List[Int] = List(10, 9, 8, 7, 6, 5, 4, 3, 2, 1)

Folds for Streams 

In Scalaz unfold defined in StreamFunctions is introduced by import Scalaz._:

scala> unfold(10) { (x) => if (x == 0) none else (x, x - 1).some }
res36: Stream[Int] = Stream(10, ?)

scala> res36.toList
res37: List[Int] = List(10, 9, 8, 7, 6, 5, 4, 3, 2, 1)

Let’s try implementing the selection sort example from the paper:

scala> def minimumS[A: Order](stream: Stream[A]) = stream match {
         case x #:: xs => xs.foldLeft(x) {_ min _}
       }
minimumS: [A](stream: Stream[A])(implicit evidence$1: scalaz.Order[A])A

scala> def deleteS[A: Equal](y: A, stream: Stream[A]): Stream[A] = (y, stream) match {
         case (_, Stream()) => Stream()
         case (y, x #:: xs) =>
           if (y === x) xs
           else x #:: deleteS(y, xs) 
       }
deleteS: [A](y: A, stream: Stream[A])(implicit evidence$1: scalaz.Equal[A])Stream[A]

scala> def delmin[A: Order](stream: Stream[A]): Option[(A, Stream[A])] = stream match {
         case Stream() => none
         case xs =>
           val y = minimumS(xs)
           (y, deleteS(y, xs)).some
       }
delmin: [A](stream: Stream[A])(implicit evidence$1: scalaz.Order[A])Option[(A, Stream[A])]

scala> def ssort[A: Order](stream: Stream[A]): Stream[A] = unfold(stream){delmin[A]}
ssort: [A](stream: Stream[A])(implicit evidence$1: scalaz.Order[A])Stream[A]

scala> ssort(Stream(1, 3, 4, 2)).toList
res55: List[Int] = List(1, 2, 3, 4)

I guess this is considered origami programming because are using foldLeft and unfold? This paper was written in 2003 as a chapter in The Fun of Programming, but I am not sure if origami programming caught on.

The Essence of the Iterator Pattern 

In 2006 the same author wrote The Essence of the Iterator Pattern. Linked is the revised 2009 version. This paper discusses applicative style by breaking down the GoF Iterator pattern into two aspects: mapping and accumulating.

The first half of the paper reviews functional iterations and applicative style. For applicative functors, it brings up the fact that there are three kinds of applicatives: 1. Monadic applicative functors 2. Naperian applicative functors 3. Monoidal applicative functors

We’ve brought up the fact that all monads are applicatives many times. Naperian applicative functor zips together data structure that are fixed in shape. Also apparently appliactive functors were originally named idiom, so idiomatic in this paper means applicative.

Monoidal applicatives 

Scalaz implements Monoid[m].applicative to turn any monoids into an applicative.

scala> Monoid[Int].applicative.ap2(1, 1)(0)
res99: Int = 2

scala> Monoid[List[Int]].applicative.ap2(List(1), List(1))(Nil)
res100: List[Int] = List(1, 1)

Combining applicative functors 

EIP:

Like monads, applicative functors are closed under products; so two independent idiomatic effects can generally be fused into one, their product.

In Scalaz, product is implemented under Applicative typeclass:

trait Applicative[F[_]] extends Apply[F] with Pointed[F] { self =>
  ...
  /**The product of Applicatives `F` and `G`, `[x](F[x], G[x]])`, is an Applicative */
  def product[G[_]](implicit G0: Applicative[G]): Applicative[({type λ[α] = (F[α], G[α])})#λ] = new ProductApplicative[F, G] {
    implicit def F = self
    implicit def G = G0
  }
  ...
}

Let’s make a product of List and Option.

scala> Applicative[List].product[Option]
res0: scalaz.Applicative[[α](List[α], Option[α])] = scalaz.Applicative$$anon$2@211b3c6a

scala> Applicative[List].product[Option].point(1)
res1: (List[Int], Option[Int]) = (List(1),Some(1))

The product seems to be implemented as a Tuple2. Let’s use Applicative style to append them:

scala> ((List(1), 1.some) |@| (List(1), 1.some)) {_ |+| _}
res2: (List[Int], Option[Int]) = (List(1, 1),Some(2))

scala> ((List(1), 1.success[String]) |@| (List(1), "boom".failure[Int])) {_ |+| _}
res6: (List[Int], scalaz.Validation[String,Int]) = (List(1, 1),Failure(boom))

EIP:

Unlike monads in general, applicative functors are also closed under composition; so two sequentially-dependent idiomatic effects can generally be fused into one, their composition.

This is called compose under Applicative:

trait Applicative[F[_]] extends Apply[F] with Pointed[F] { self =>
...
  /**The composition of Applicatives `F` and `G`, `[x]F[G[x]]`, is an Applicative */
  def compose[G[_]](implicit G0: Applicative[G]): Applicative[({type λ[α] = F[G[α]]})#λ] = new CompositionApplicative[F, G] {
    implicit def F = self
    implicit def G = G0
  }
...
}

Let’s compose List and Option.

scala> Applicative[List].compose[Option]
res7: scalaz.Applicative[[α]List[Option[α]]] = scalaz.Applicative$$anon$1@461800f1

scala> Applicative[List].compose[Option].point(1)
res8: List[Option[Int]] = List(Some(1))

EIP:

The two operators ⊗ and ⊙ allow us to combine idiomatic computations in two different ways; we call them parallel and sequential composition, respectively.

The fact that we can compose applicatives and it remain applicative is neat. I am guessing that this characteristics enables modularity later in this paper.

Idiomatic traversal 

EIP:

Traversal involves iterating over the elements of a data structure, in the style of a map, but interpreting certain function applications idiomatically.

The corresponding typeclass in Scalaz 7 is called Traverse:

trait Traverse[F[_]] extends Functor[F] with Foldable[F] { self =>
  def traverseImpl[G[_]:Applicative,A,B](fa: F[A])(f: A => G[B]): G[F[B]]
}

This introduces traverse operator:

trait TraverseOps[F[_],A] extends Ops[F[A]] {
  final def traverse[G[_], B](f: A => G[B])(implicit G: Applicative[G]): G[F[B]] =
    G.traverse(self)(f)
  ...
}

Here’s how we can use it for List:

scala> List(1, 2, 3) traverse { x => (x > 0) option (x + 1) }
res14: Option[List[Int]] = Some(List(2, 3, 4))

scala> List(1, 2, 0) traverse { x => (x > 0) option (x + 1) }
res15: Option[List[Int]] = None

The option operator is injected to Boolean, which expands (x > 0) option (x + 1) to if (x > 0) Some(x + 1) else None.

EIP:

In the case of a monadic applicative functor, traversal specialises to monadic map, and has the same uses.

It does have have similar feel to flatMap, except now the passed in function returns G[B] where [G: Applicative] instead of requiring List.

EIP:

For a monoidal applicative functor, traversal accumulates values. The function reduce performs that accumulation, given an argument that assigns a value to each element.

scala> Monoid[Int].applicative.traverse(List(1, 2, 3)) {_ + 1}
res73: Int = 9

I wasn’t able to write this as traverse operator.

Shape and contents 

EIP:

In addition to being parametrically polymorphic in the collection elements, the generic traverse operation is parametrised along two further dimensions: the datatype being traversed, and the applicative functor in which the traversal is interpreted. Specialising the latter to lists as a monoid yields a generic contents operation.

scala> def contents[F[_]: Traverse, A](f: F[A]): List[A] =
         Monoid[List[A]].applicative.traverse(f) {List(_)}
contents: [F[_], A](f: F[A])(implicit evidence$1: scalaz.Traverse[F])List[A]

scala> contents(List(1, 2, 3))
res87: List[Int] = List(1, 2, 3)

scala> contents(NonEmptyList(1, 2, 3))
res88: List[Int] = List(1, 2, 3)

scala> val tree: Tree[Char] = 'P'.node('O'.leaf, 'L'.leaf)
tree: scalaz.Tree[Char] = <tree>

scala> contents(tree)
res90: List[Char] = List(P, O, L)

Now we can take any data structure that supports Traverse and turn it into a List. We can also write contents as follows:

scala> def contents[F[_]: Traverse, A](f: F[A]): List[A] =
         f.traverse[({type l[X]=List[A]})#l, A] {List(_)}
contents: [F[_], A](f: F[A])(implicit evidence$1: scalaz.Traverse[F])List[A]

The other half of the decomposition is obtained simply by a map, which is to say, a traversal interpreted in the identity idiom.

The “identity idiom” is the Id monad in Scalaz.

scala> def shape[F[_]: Traverse, A](f: F[A]): F[Unit] =
  f traverse {_ => ((): Id[Unit])}
shape: [F[_], A](f: F[A])(implicit evidence$1: scalaz.Traverse[F])F[Unit]

scala> shape(List(1, 2, 3))
res95: List[Unit] = List((), (), ())

scala> shape(tree).drawTree
res98: String =
"()
|
()+-
|
()`-
"

EIP:

This pair of traversals nicely illustrates the two aspects of iterations that we are focussing on, namely mapping and accumulation.

Let’s also implement decompose function:

scala> def decompose[F[_]: Traverse, A](f: F[A]) = (shape(f), contents(f))
decompose: [F[_], A](f: F[A])(implicit evidence$1: scalaz.Traverse[F])(F[Unit], List[A])

scala> decompose(tree)
res110: (scalaz.Tree[Unit], List[Char]) = (<tree>,List(P, O, L))

This works, but it’s looping the tree structure twice. Remember a product of two applicatives are also an applicative?

scala> def decompose[F[_]: Traverse, A](f: F[A]) =
         Applicative[Id].product[({type l[X]=List[A]})#l].traverse(f) { x => (((): Id[Unit]), List(x)) }
decompose: [F[_], A](f: F[A])(implicit evidence$1: scalaz.Traverse[F])(scalaz.Scalaz.Id[F[Unit]], List[A])

scala> decompose(List(1, 2, 3, 4))
res135: (scalaz.Scalaz.Id[List[Unit]], List[Int]) = (List((), (), (), ()),List(1, 2, 3, 4))

scala> decompose(tree)
res136: (scalaz.Scalaz.Id[scalaz.Tree[Unit]], List[Char]) = (<tree>,List(P, O, L))

Since the above implementation relys on type annotation to get the monoidal applicative functor, I can’t write it as nice as the Haskell example:

decompose = traverse (shapeBody ⊗ contentsBody)

Sequence 

There’s a useful method that Traverse introduces called sequence. The names comes from Haskell’s sequence function, so let’s Hoogle it:

`haskell sequence :: Monad m => [m a] -> m [a]` Evaluate each action in the sequence from left to right, and collect the results.

Here’s sequence method:

  /** Traverse with the identity function */
  final def sequence[G[_], B](implicit ev: A === G[B], G: Applicative[G]): G[F[B]] = {
    val fgb: F[G[B]] = ev.subst[F](self)
    F.sequence(fgb)
  }

Instead of Monad, the requirement is relaxed to Applicative. Here’s how we can use it:

scala> List(1.some, 2.some).sequence
res156: Option[List[Int]] = Some(List(1, 2))

scala> List(1.some, 2.some, none).sequence
res157: Option[List[Int]] = None

This looks cool. And because it’s a Traverse method, it’ll work for other data structures as well:

scala> val validationTree: Tree[Validation[String, Int]] = 1.success[String].node(
         2.success[String].leaf, 3.success[String].leaf)
validationTree: scalaz.Tree[scalaz.Validation[String,Int]] = <tree>

scala> validationTree.sequence[({type l[X]=Validation[String, X]})#l, Int]
res162: scalaz.Validation[String,scalaz.Unapply[scalaz.Traverse,scalaz.Tree[scalaz.Validation[String,Int]]]{type M[X] = scalaz.Tree[X]; type A = scalaz.Validation[String,Int]}#M[Int]] = Success(<tree>)

scala> val failedTree: Tree[Validation[String, Int]] = 1.success[String].node(
         2.success[String].leaf, "boom".failure[Int].leaf)
failedTree: scalaz.Tree[scalaz.Validation[String,Int]] = <tree>

scala> failedTree.sequence[({type l[X]=Validation[String, X]})#l, Int]
res163: scalaz.Validation[String,scalaz.Unapply[scalaz.Traverse,scalaz.Tree[scalaz.Validation[String,Int]]]{type M[X] = scalaz.Tree[X]; type A = scalaz.Validation[String,Int]}#M[Int]] = Failure(boom)

Collection and dispersal 

EIP:

We have found it convenient to consider special cases of effectful traversals, in which the mapping aspect is independent of the accumulation, and vice versa. The first of these traversals accumulates elements effectfully, with an operation of type a → m (), but modifies those elements purely and independently of this accumulation, with a function of type a → b.

This is mimicking the use of for loop with mutable variable accumulating the value outside of the loop. Traverse adds traverseS, which is a specialized version of traverse for State monad. Using that we can write collect as following:

scala> def collect[F[_]: Traverse, A, S, B](t: F[A])(f: A => B)(g: S => S) =
         t.traverseS[S, B] { a => State { (s: S) => (g(s), f(a)) } }
collect: [F[_], A, S, B](t: F[A])(f: A => B)(g: S => S)(implicit evidence$1: scalaz.Traverse[F])scalaz.State[S,scalaz.Unapply[scalaz.Traverse,F[A]]{type M[X] = F[X]; type A = A}#M[B]]

scala> val loop = collect(List(1, 2, 3, 4)) {(_: Int) * 2} {(_: Int) + 1}
loop: scalaz.State[Int,scalaz.Unapply[scalaz.Traverse,List[Int]]{type M[X] = List[X]; type A = Int}#M[Int]] = scalaz.package$State$$anon$1@3926008a

scala> loop(0)
res165: (Int, scalaz.Unapply[scalaz.Traverse,List[Int]]{type M[X] = List[X]; type A = Int}#M[Int]) = (4,List(2, 4, 6, 8))

EIP:

The second kind of traversal modifies elements purely but dependent on the state, with a binary function of type a → b → c, evolving this state independently of the elements, via a computation of type m b.

This is the same as traverseS. Here’s how we can implement label:

scala> def label[F[_]: Traverse, A](f: F[A]): F[Int] =
         (f.traverseS {_ => for {
           n <- get[Int]
           x <- put(n + 1)
         } yield n}) eval 0
label: [F[_], A](f: F[A])(implicit evidence$1: scalaz.Traverse[F])F[Int]

It’s ignoring the content of the data structure, and replacing it with a number starting with 0. Very effecty. Here’s how it looks with List and Tree:

scala> label(List(10, 2, 8))
res176: List[Int] = List(0, 1, 2)

scala> label(tree).drawTree
res177: String =
"0
|
1+-
|
2`-
"

Links 

EIP seems to be a popular paper to cover among Scala fp people.

Eric Torreborre (@etorreborre)’s The Essence of the Iterator Pattern is the most thorough study of the paper. It also covers lots of ground works, so it’s worth digging in.

Debasish Ghosh (@debasishg)’s Iteration in Scala - effectful yet functional is shorter but covering the good part by focusing on Scalaz.

Marc-Daniel Ortega (@patterngazer)’s Where we traverse, accumulate and collect in Scala also covers sequence and collect using Scalaz.

We’ll pick it up from here later.

day 13 (import guide) 

e.e d3si9n

Yesterday we skimmed two papers by Jeremy Gibbons and quickly looked at origami programming and applicative traversal. Instead of reading something, why don’t we focus on using Scalaz today.

implicits review 

Scalaz makes heavy use of implicits. Both as a user and an extender of the library, it’s important to have general idea on where things are coming from. Let’s quickly review Scala’s imports and implicits!

In Scala, imports are used for two purposes: 1. To include names of values and types into the scope. 2. To include implicits into the scope.

Implicits are for 4 purposes that I can think of: 1. To provide typeclass instances. 2. To inject methods and operators. (static monkey patching) 3. To declare type constraints. 4. To retrieve type information from compiler.

Implicits are selected in the following precedence: 1. Values and converters accessible without prefix via local declaration, imports, outer scope, inheritance, and current package object. Inner scope can shadow values when they are named the same. 2. Implicit scope. Values and converters declared in companion objects and package object of the type, its parts, or super types.

import scalaz._ 

Now let’s see what gets imported with import scalaz._.

First, the names. Typeclasses like Equal[A] and Functor[F[_]] are implemented as trait, and are defined under scalaz package. So instead of writing scalaz.Equal[A] we can write Equal[A].

Next, also the names, but type aliases. scalaz’s package object declares most of the major type aliases like @@[T, Tag] and Reader[E, A], which is treated as a specialization of ReaderT transformer. Again, these can also be accessed as scalaz.Reader[E, A] if you want.

Finally, idInstance is defined as typeclass instance of Id[A] for Traverse[F[_]], Monad[F[_]] etc, but it’s not relevant. By virtue of declaring an instance within its package object it will be available, so importing doesn’t add much. Let’s check this:

scala> scalaz.Monad[scalaz.Id.Id]
res1: scalaz.Monad[scalaz.Id.Id] = scalaz.IdInstances$$anon$1@fc98c94

No import needed, which is a good thing. So, the merit of import scalaz._ is for convenience, and it’s optional.

import Scalaz._ 

What then is import Scalaz._ doing? Here’s the definition of Scalaz object:

package scalaz

object Scalaz
  extends StateFunctions        // Functions related to the state monad
  with syntax.ToTypeClassOps    // syntax associated with type classes
  with syntax.ToDataOps         // syntax associated with Scalaz data structures
  with std.AllInstances         // Type class instances for the standard library types
  with std.AllFunctions         // Functions related to standard library types
  with syntax.std.ToAllStdOps   // syntax associated with standard library types
  with IdInstances              // Identity type and instances

This is quite a nice way of organizing the imports. Scalaz object itself doesn’t define anythig and it just mixes in the traits. We are going to look at each traits in detail, but they can also be imported a la carte, dim sum style. Back to the full course.

StateFunctions 

Remember, import brings in names and implicits. First, the names. StateFunctions defines several functions:

package scalaz

trait StateFunctions {
  def constantState[S, A](a: A, s: => S): State[S, A] = ...
  def state[S, A](a: A): State[S, A] = ...
  def init[S]: State[S, S] = ...
  def get[S]: State[S, S] = ...
  def gets[S, T](f: S => T): State[S, T] = ...
  def put[S](s: S): State[S, Unit] = ...
  def modify[S](f: S => S): State[S, Unit] = ...
  def delta[A](a: A)(implicit A: Group[A]): State[A, A] = ...
}

By bringing these functions in we can treat get and put like a global function. Why? This enables DSL we saw on day 7:

for {
  xs <- get[List[Int]]
  _ <- put(xs.tail)
} yield xs.head

std.AllFunctions 

Second, the names again. std.AllFunctions is actually a mixin of traits itself:

package scalaz
package std

trait AllFunctions
  extends ListFunctions
  with OptionFunctions
  with StreamFunctions
  with math.OrderingFunctions
  with StringFunctions

object AllFunctions extends AllFunctions

Each of the above trait bring in various functions into the scope that acts as a global function. For example, ListFunctions bring in intersperse function that puts a given element in ever other position:

scala> intersperse(List(1, 2, 3), 7)
res3: List[Int] = List(1, 7, 2, 7, 3)

It’s ok. Since I personally use injected methods, I don’t have much use to these functions.

IdInstances 

Although it’s named IdInstances, it also defines the type alias Id[A] as follows:

  type Id[+X] = X

That’s it for the names. Imports can bring in implicits, and I said there are four uses for the implicits. We mostly care about the first two: typeclass instances and injected methods and operators.

std.AllInstances 

Thus far, I have been intentionally conflating the concept of typeclass instances and method injection (aka enrich my library). But the fact that List is a Monad and that Monad introduces >>= operator are two different things.

One of the most interesting design of Scalaz 7 is that it rigorously separates the two concepts into “instance” and “syntax.” Even if it makes logical sense to some users, the choice of symbolic operators can often be a point of contention with any libraries. Libraries and tools such as sbt, dispatch, and specs introduce its own DSL, and their effectiveness have been hotly debated. To make the matter complicated, injected methods may conflict with each other when more than one DSLs are used together.

std.AllInstances is a mixin of typeclass instances for built-in (std) data structures:

package scalaz.std

trait AllInstances
  extends AnyValInstances with FunctionInstances with ListInstances with MapInstances
  with OptionInstances with SetInstances with StringInstances with StreamInstances with TupleInstances
  with EitherInstances with PartialFunctionInstances with TypeConstraintInstances
  with scalaz.std.math.BigDecimalInstances with scalaz.std.math.BigInts
  with scalaz.std.math.OrderingInstances
  with scalaz.std.util.parsing.combinator.Parsers
  with scalaz.std.java.util.MapInstances
  with scalaz.std.java.math.BigIntegerInstances
  with scalaz.std.java.util.concurrent.CallableInstances
  with NodeSeqInstances
  // Intentionally omitted: IterableInstances

object AllInstances extends AllInstances

syntax.ToTypeClassOps 

Next are the injected methods and operators. All of them are defined under scalaz.syntax package. syntax.ToTypeClassOps introduces all the injected methods for typeclasses:

package scalaz
package syntax

trait ToTypeClassOps
  extends ToSemigroupOps with ToMonoidOps with ToGroupOps with ToEqualOps with ToLengthOps with ToShowOps
  with ToOrderOps with ToEnumOps with ToMetricSpaceOps with ToPlusEmptyOps with ToEachOps with ToIndexOps
  with ToFunctorOps with ToPointedOps with ToContravariantOps with ToCopointedOps with ToApplyOps
  with ToApplicativeOps with ToBindOps with ToMonadOps with ToCojoinOps with ToComonadOps
  with ToBifoldableOps with ToCozipOps
  with ToPlusOps with ToApplicativePlusOps with ToMonadPlusOps with ToTraverseOps with ToBifunctorOps
  with ToBitraverseOps with ToArrIdOps with ToComposeOps with ToCategoryOps
  with ToArrowOps with ToFoldableOps with ToChoiceOps with ToSplitOps with ToZipOps with ToUnzipOps with ToMonadWriterOps with ToListenableMonadWriterOps

For example, [syntax.ToBindOps] implicitly converts F[A] where [F: Bind] into BindOps[F, A] that implements >>= operator.

syntax.ToDataOps 

syntax.ToDataOps introduces injected methods for data structures defined in Scalaz:

trait ToDataOps extends ToIdOps with ToTreeOps with ToWriterOps with ToValidationOps with ToReducerOps with ToKleisliOps

IdOps methods are injected to all types, and are mostly there for convenience:

package scalaz.syntax

trait IdOps[A] extends Ops[A] {
  final def ??(d: => A)(implicit ev: Null <:< A): A = ...
  final def |>[B](f: A => B): B = ...
  final def squared: (A, A) = ...
  def left[B]: (A \/ B) = ...
  def right[B]: (B \/ A) = ...
  final def wrapNel: NonEmptyList[A] = ...
  def matchOrZero[B: Monoid](pf: PartialFunction[A, B]): B = ...
  final def doWhile(f: A => A, p: A => Boolean): A = ...
  final def whileDo(f: A => A, p: A => Boolean): A = ...
  def visit[F[_] : Pointed](p: PartialFunction[A, F[A]]): F[A] = ...
}

trait ToIdOps {
  implicit def ToIdOps[A](a: A): IdOps[A] = new IdOps[A] {
    def self: A = a
  }
}

Interestingly, ToTreeOps converts all data types to TreeOps[A] injecting two methods:

package scalaz
package syntax

trait TreeOps[A] extends Ops[A] {
  def node(subForest: Tree[A]*): Tree[A] = ...
  def leaf: Tree[A] = ...
}

trait ToTreeOps {
  implicit def ToTreeOps[A](a: A) = new TreeOps[A]{ def self = a }
}

So these are injected methods to create Tree.

scala> 1.node(2.leaf)
res7: scalaz.Tree[Int] = <tree>

The same goes for WriterOps[A], ValidationOps[A], ReducerOps[A], and KleisliIdOps[A]:

scala> 1.set("log1")
res8: scalaz.Writer[String,Int] = scalaz.WriterTFunctions$$anon$26@2375d245

scala> "log2".tell
res9: scalaz.Writer[String,Unit] = scalaz.WriterTFunctions$$anon$26@699289fb

scala> 1.success[String]
res11: scalaz.Validation[String,Int] = Success(1)

scala> "boom".failureNel[Int]
res12: scalaz.ValidationNEL[String,Int] = Failure(NonEmptyList(boom))

So most of the mixins under syntax.ToDataOps introduces methods to all types to create Scalaz data structure.

syntax.std.ToAllStdOps 

Finally, we have syntax.std.ToAllStdOps, which introduces methods and operators to Scala’s standard types.

package scalaz
package syntax
package std

trait ToAllStdOps
  extends ToBooleanOps with ToOptionOps with ToOptionIdOps with ToListOps with ToStreamOps
  with ToFunction2Ops with ToFunction1Ops with ToStringOps with ToTupleOps with ToMapOps with ToEitherOps

This is the fun stuff. BooleanOps introduces shorthands for all sorts of things:

scala> false /\ true
res14: Boolean = false

scala> false \/ true
res15: Boolean = true

scala> true option "foo"
res16: Option[String] = Some(foo)

scala> (1 > 10)? "foo" | "bar"
res17: String = bar

scala> (1 > 10)?? {List("foo")}
res18: List[String] = List()

The option operator is very useful. The ternary operator looks like a shorter notation than if-else.

OptionOps also introduces something similar:

scala> 1.some? "foo" | "bar"
res28: String = foo

scala> 1.some | 2
res30: Int = 1

On the other hand ListOps introduced traditional Monad related things:

scala> List(1, 2) filterM {_ => List(true, false)}
res37: List[List[Int]] = List(List(1, 2), List(1), List(2), List())

a la carte style 

Or, I’d like to call dim sum style, where they bring in a cart load of chinese dishes and you pick what you want.

If for whatever reason if you do not wish to import the entire Scalaz._, you can pick and choose.

typeclass instances and functions 

Typeclass instances are broken down by the data structures. Here’s how to get all typeclass instances for Option:

// fresh REPL
scala> import scalaz.std.option._
import scalaz.std.option._

scala> scalaz.Monad[Option].point(0)
res0: Option[Int] = Some(0)

This also brings in the “global” helper functions related to Option. Scala standard data structures are found under scalaz.std package.

If you just want all instances, here’s how to load them all:

scala> import scalaz.std.AllInstances._
import scalaz.std.AllInstances._

scala> scalaz.Monoid[Int]
res2: scalaz.Monoid[Int] = scalaz.std.AnyValInstances$$anon$3@784e6f7c

Because we have not injected any operators, you would have to work more with helper functions and functions under typeclass instances, which could be exactly what you want.

Scalaz typeclass syntax 

Typeclass syntax are broken down by the typeclass. Here’s how to get injected methods and operators for Monads:

scala> import scalaz.syntax.monad._
import scalaz.syntax.monad._

scala> import scalaz.std.option._
import scalaz.std.option._

scala> 0.point[Option]
res0: Option[Int] = Some(0)

As you can see, not only Monad method was injected but also Pointed methods got in too.

Scalaz data structure syntax like Tree are also available under scalaz.syntax package. Here’s how to load all syntax for both the typeclasses and Scalaz’s data structure:

scala> import scalaz.syntax.all._
import scalaz.syntax.all._

scala> 1.leaf
res0: scalaz.Tree[Int] = <tree>

standard data structure syntax 

Standard data structure syntax are broken down by the data structure. Here’s how to get injected methods and operators for Boolean:

// fresh REPL
scala> import scalaz.syntax.std.boolean._
import scalaz.syntax.std.boolean._

scala> (1 > 10)? "foo" | "bar"
res0: String = bar

To load all the standard data structure syntax in:

// fresh REPL
scala> import scalaz.syntax.std.all._
import scalaz.syntax.std.all._

scala> 1.some | 2
res1: Int = 1

I thought this would be a quick thing, but it turned out to be an entire post. We’ll pick it up from here.

day 14 

bman ojel for openphoto.net

Yesterday we looked at what import scalaz._ and Scalaz._ bring into the scope, and also talked about a la carte style import. Knowing how instances and syntax are organized prepares us for the next step, which is to hack on Scalaz.

mailing list 

Before we start hacking on a project, it’s probably good idea to join its Google Group.

git clone 

$ git clone -b series/7.1.x git://github.com/scalaz/scalaz.git scalaz

The above should clone series/7.1.x branch into ./scalaz directory. Next I edited the .git/config as follows:

[core]
  repositoryformatversion = 0
  filemode = true
  bare = false
  logallrefupdates = true
  ignorecase = true
[remote "upstream"]
  fetch = +refs/heads/*:refs/remotes/origin/*
  url = git://github.com/scalaz/scalaz.git
[branch "series/7.1.x"]
  remote = upstream
  merge = refs/heads/series/7.1.x

This way, scalaz/scalaz is referenced using the name upstream instead of origin. To track the changes, run:

$ git pull --rebase
Current branch series/7.1.x is up to date.

sbt 

Next, launch sbt 0.13.5, set scala version to 2.11.1, switch to core project, and compile:

$ sbt
scalaz> ++ 2.11.1
Setting version to 2.11.1
[info] Set current project to scalaz (in build file:/Users/eed3si9n/work/scalaz/)
scalaz> project core
[info] Set current project to scalaz-core (in build file:/Users/eed3si9n/work/scalaz/)
scalaz-core> compile

This might take a few minutes. Let’s make sure this builds a snapshot version:

scalaz-core> version
[info] 7.0-SNAPSHOT

To try out the locally compiled Scalaz, just get into the REPL as usual using console:

scalaz-core> console
[info] Starting scala interpreter...
[info]
Welcome to Scala version 2.10.1 (Java HotSpot(TM) 64-Bit Server VM, Java 1.6.0_33).
Type in expressions to have them evaluated.
Type :help for more information.

scala> [Ctrl + D to exit]

including Vector 

Let’s address some of the things we’ve noticed in the last few weeks. For example, I think Vector instances should be part of import Scalaz._. This should be easy while my memory is fresh from yesterday’s import review. Let’s make a topic branch topic/vectorinstance:

$ git branch topic/vectorinstance
$ git co topic/vectorinstance
Switched to branch 'topic/vectorinstance'

To confirm that Vector instances and methods are not loaded in by import Scalaz._, let’s check it from sbt console:

$ sbt
scalaz> ++ 2.11.1
scalaz> project core
scalaz-core> console
scala> import scalaz._
import scalaz._

scala> import Scalaz._
import Scalaz._

scala> Vector(1, 2) >>= { x => Vector(x + 1)}
<console>:14: error: could not find implicit value for parameter F0: scalaz.Bind[scala.collection.immutable.Vector]
              Vector(1, 2) >>= { x => Vector(x + 1)}
                    ^

scala> Vector(1, 2) filterM { x => Vector(true, false) }
<console>:14: error: value filterM is not a member of scala.collection.immutable.Vector[Int]
              Vector(1, 2) filterM { x => Vector(true, false) }
                           ^

Failed as expected.

Update std.AllInstances by mixing in VectorInstances:

trait AllInstances
  extends AnyValInstances with FunctionInstances with ListInstances with MapInstances
  with OptionInstances with SetInstances with StringInstances with StreamInstances
  with TupleInstances with VectorInstances
  ...

Update syntax.std.ToAllStdOps and add ToVectorOps:

trait ToAllStdOps
  extends ToBooleanOps with ToOptionOps with ToOptionIdOps with ToListOps with ToStreamOps with ToVectorOps
  ...

That’s it. Let’s try it from REPL.

scala> Vector(1, 2) >>= { x => Vector(x + 1)}
res0: scala.collection.immutable.Vector[Int] = Vector(2, 3)

scala> Vector(1, 2) filterM { x => Vector(true, false) }
res1: scala.collection.immutable.Vector[Vector[Int]] = Vector(Vector(1, 2), Vector(1), Vector(2), Vector())

It works. I didn’t see tests written for these type of things, so we’ll go without one. I committed it as “include VectorInstances and ToVectorOps to import Scalaz._.” Next, fork scalaz project on github.

$ git remote add fork git@github.com:yourname/scalaz.git
$ git push fork topic/vectorinstance
...
 * [new branch]      topic/vectorinstance -> topic/vectorinstance

Send a pull request with some comments, and let’s see what happens. To work on a next feature, we want to rewind back to scalaz-seven branch. For using locally, let’s create a snapshot branch:

snapshot 

$ git co scalaz-seven
Switched to branch 'scalaz-seven'
$ git branch snapshot
$ git co snapshot
$ git merge topic/vectorinstance

We can use this branch as a sandbox to play around with Scalaz.

<*> operator 

Next, I’d really like to roll back <*> operator for Apply back to M2/Haskell behavior. I’ve asked this on the mailing list and the author seems to be ok with rolling back.

$ git co scalaz-seven
Switched to branch 'scalaz-seven'
$ git branch topic/applyops
$ git co topic/applyops
Switched to branch 'topic/applyops'

This one we really should write a test first. Let’s add an example in ApplyTest:

  "<*>" in {
    some(9) <*> some({(_: Int) + 3}) must be_===(some(12))
  }

The specs used in build.scala works for Scala 2.9.2.

$ sbt
scalaz> ++ 2.9.2
Setting version to 2.9.2
scalaz> project tests
scalaz-tests> test-only scalaz.ApplyTest
[error] /Users/eed3si9n/work/scalaz-seven/tests/src/test/scala/scalaz/ApplyTest.scala:38: type mismatch;
[error]  found   : org.specs2.matcher.Matcher[Option[Int]]
[error]  required: org.specs2.matcher.Matcher[Option[(Int, Int => Int)]]
[error]     some(9) <*> some({(_: Int) + 3}) must be_===(some(12))
[error]                                                 ^
[error] one error found
[error] (tests/test:compile) Compilation failed

It didn’t even compile because of ===. Nice.

The <*> is in ApplyOps, so let’s change it back to F.ap:

  final def <*>[B](f: F[A => B]): F[B] = F.ap(self)(f)

Now let’s run the test again:

scalaz-tests> test-only scalaz.ApplyTest
[info] ApplyTest
[info]
[info] + mapN
[info] + apN
[info] + <*>
[info]  
[info] Total for specification ApplyTest
[info] Finished in 5 seconds, 27 ms
[info] 3 examples, 0 failure, 0 error
[info]
[info] Passed: : Total 3, Failed 0, Errors 0, Passed 3, Skipped 0
[success] Total time: 9 s, completed Sep 19, 2012 1:57:29 AM

I am committing this as “roll back <*> as infix of ap” and pushing it out.

$ git push fork topic/applyops
...
 * [new branch]      topic/applyops -> topic/applyops

Send a pull request with some comments. Let’s apply this to our snapshot branch:

$ git co snapshot
$ git merge topic/applyops

So now it has both of the changes we created.

applicative functions 

The changed we made were so far simple fixes. From here starts an experiment. It’s about applicative functions.

The Essence of the Iterator Pattern presents an interesting idea of combining applicative functors. What’s actually going on is not just the combination of applicative functors (m ⊠ n), but the combination of applicative functions:

(⊗)::(Functor m,Functor n) ⇒ (a → m b) → (a → n b) → (a → (m ⊠ n) b)
(f ⊗ g) x = Prod (f x) (g x)

Int is a Monoid, and any Monoid can be treated as an applicative functor, which is called monoidal applicatives. The problem is that when we make that into a function, it’s not distinguishable from Int => Int, but we need Int => [α]Int.

My first idea was to use type tags named Tags.Monoidal, so the idea is to make it:

scala> { (x: Int) => Tags.Monoidal(x + 1) }

This requires all A @@ Tags.Monoidal where [A:Monoid] to be recognized as an applicative. I got stuck on that step.

Next idea was to make Monoidal an alias of Kleisli with the following companion:

  object Monoidal {
    def apply[A: Monoid](f: A => A): Kleisli[({type λ[+α]=A})#λ, A, A] =
      Kleisli[({type λ[+α]=A})#λ, A, A](f)
  }

This let’s me write monoidal functions as follows:

scala> Monoidal { x: Int => x + 1 }
res4: scalaz.Kleisli[[+α]Int,Int,Int] = scalaz.KleisliFunctions$$anon$18@1a0ceb34

But the compiler did not find Applicative automatically from [+α]Int:

scala> List(1, 2, 3) traverseKTrampoline { x => Monoidal { _: Int => x + 1 } }
<console>:14: error: no type parameters for method traverseKTrampoline: (f: Int => scalaz.Kleisli[G,S,B])(implicit evidence$2: scalaz.Applicative[G])scalaz.Kleisli[G,S,List[B]] exist so that it can be applied to arguments (Int => scalaz.Kleisli[[+α]Int,Int,Int])
 --- because ---
argument expression's type is not compatible with formal parameter type;
 found   : Int => scalaz.Kleisli[[+α]Int,Int,Int]
 required: Int => scalaz.Kleisli[?G,?S,?B]

              List(1, 2, 3) traverseKTrampoline { x => Monoidal { _: Int => x + 1 } }
                            ^

Is this the infamous SI-2712? Then I thought, ok I’ll turn this into an actual type:

trait MonoidApplicative[F] extends Applicative[({type λ[α]=F})#λ] { self =>
  implicit def M: Monoid[F]
  def point[A](a: => A) = M.zero
  def ap[A, B](fa: => F)(f: => F) = M.append(f, fa)
  override def map[A, B](fa: F)(f: (A) => B) = fa
}

This does not work because now we have to convert x + 1 into MonoidApplicative.

Next I thought about giving Unapply a shot:

scala> List(1, 2, 3) traverseU {_ + 1}
<console>:14: error: Unable to unapply type `Int` into a type constructor of kind `M[_]` that is classified by the type class `scalaz.Applicative`
1) Check that the type class is defined by compiling `implicitly[scalaz.Applicative[<type constructor>]]`.
2) Review the implicits in object Unapply, which only cover common type 'shapes'
(implicit not found: scalaz.Unapply[scalaz.Applicative, Int])
              List(1, 2, 3) traverseU {_ + 1}
                            ^

This could work. All we have to do is unpack Int as ({type λ[α]=Int})#λ in Unapply:

trait Unapply_3 {
  /** Unpack a value of type `A0` into type `[a]A0`, given a instance of `TC` */
  implicit def unapplyA[TC[_[_]], A0](implicit TC0: TC[({type λ[α] = A0})#λ]): Unapply[TC, A0] {
    type M[X] = A0
    type A = A0
  } = new Unapply[TC, A0] {
    type M[X] = A0
    type A = A0
    def TC = TC0
    def apply(ma: M[A0]) = ma
  }
}

Let’s try:

scala> List(1, 2, 3) traverseU {_ + 1}
res0: Int = 9

This actually worked! Can we combine this?

scala> val f = { (x: Int) => x + 1 }
f: Int => Int = <function1>

scala> val g = { (x: Int) => List(x, 5) }
g: Int => List[Int] = <function1>

scala> val h = f &&& g
h: Int => (Int, List[Int]) = <function1>

scala> List(1, 2, 3) traverseU f
res0: Int = 9

scala> List(1, 2, 3) traverseU g
res1: List[List[Int]] = List(List(1, 2, 3), List(1, 2, 5), List(1, 5, 3), List(1, 5, 5), List(5, 2, 3), List(5, 2, 5), List(5, 5, 3), List(5, 5, 5))

scala> List(1, 2, 3) traverseU h
res2: (Int, List[List[Int]]) = (9,List(List(1, 5), List(2, 5), List(3, 5)))

I am guessing either res1 or res2 is wrong. res1 is what traverse is supposed to return at least from what I checked in Haskell. Because Tuple2 is also an applicative it’s doing something unexpected. I was able to confirm this behavior without my changes, so let’s add a test:

    "traverse int function as monoidal applicative" in {
      val s: Int = List(1, 2, 3) traverseU {_ + 1}
      s must be_===(9)
    }

Let’s run it:

scalaz-tests> test-only scalaz.TraverseTest
[info] list should
[info] + apply effects in order
[info] + traverse through option effect
[info] + traverse int function as monoidal applicative
[info] + not blow the stack
[info] + state traverse agrees with regular traverse
[info] + state traverse does not blow stack
...
[success] Total time: 183 s, completed Sep 19, 2012 8:09:03 AM

Branch out from scalaz-seven and make topic/unapplya branch:

$ git co scalaz-seven
M core/src/main/scala/scalaz/Unapply.scala
M tests/src/test/scala/scalaz/TraverseTest.scala
Switched to branch 'scalaz-seven'
$ git branch topic/unapplya
$ git co topic/unapplya
M core/src/main/scala/scalaz/Unapply.scala
M tests/src/test/scala/scalaz/TraverseTest.scala
Switched to branch 'topic/unapplya'

If all the tests pass, I am committing this as “adds implicit def unapplyA, which unpacks A into [a]A.”

$ git push fork topic/unapplya
...
 * [new branch]      topic/unapplya -> topic/unapplya

Let’s send this as a pull request too. This was fun.

We’ll pick it up from here later.

day 15 

On day 14 we started hacking on Scalaz. First, typeclass instances for Vector was added to import Scalaz._. Next, we rolled back <*> to be infix ap. Finally, we added an implicit converter to unpack A as [α]A, which helps compiler find Applicative[({type λ[α]=Int})#λ].

All three of the pull requests were accepted by the upstream! Here’s how to sync up:

$ git co scalaz-seven
$ git pull --rebase

Let’s take a moment to see some of the typeclasses I was looking.

Rodolfo Cartas for openphoto.net

Arrow 

An arrow is the term used in category theory as an abstract notion of thing that behaves like a function. In Scalaz, these are Function1[A, B], PartialFunction[A, B], Kleisli[F[_], A, B], and CoKleisli[F[_], A, B]. Arrow abstracts them all similar to the way other typeclasses abtracts containers.

Here is the typeclass contract for Arrow:

trait Arrow[=>:[_, _]] extends Category[=>:] { self =>
  def id[A]: A =>: A
  def arr[A, B](f: A => B): A =>: B
  def first[A, B, C](f: (A =>: B)): ((A, C) =>: (B, C))
}

Looks like Arrow[=>:[_, _]] extends Category[=>:].

Category and Compose 

Here’s Category[=>:[_, _]]:

trait Category[=>:[_, _]] extends Compose[=>:] { self =>
  /** The left and right identity over `compose`. */
  def id[A]: A =>: A
}

This extends Compose[=>:]:

trait Compose[=>:[_, _]]  { self =>
  def compose[A, B, C](f: B =>: C, g: A =>: B): (A =>: C)
}

compose function composes two arrows into one. Using compose, Compose introduces the following operators:

trait ComposeOps[F[_, _],A, B] extends Ops[F[A, B]] {
  final def <<<[C](x: F[C, A]): F[C, B] = F.compose(self, x)
  final def >>>[C](x: F[B, C]): F[A, C] = F.compose(x, self)
}

The meaning of >>> and <<< depends on the arrow, but for functions, it’s the same as andThen and compose:

scala> val f = (_:Int) + 1
f: Int => Int = <function1>

scala> val g = (_:Int) * 100
g: Int => Int = <function1>

scala> (f >>> g)(2)
res0: Int = 300

scala> (f <<< g)(2)
res1: Int = 201

Arrow, again 

The type signature of Arrow[=>:[_, _]] looks a bit odd, but this is no different than saying Arrow[M[_, _]]. The neat things about type constructor that takes two type parameters is that we can write =>:[A, B] as A =>: B.

arr function creates an arrow from a normal function, id returns an identity arrow, and first creates a new arrow from an existing arrow by expanding the input and output as pairs.

Using the above functions, arrows introduces the following operators:

trait ArrowOps[F[_, _],A, B] extends Ops[F[A, B]] {
  final def ***[C, D](k: F[C, D]): F[(A, C), (B, D)] = F.splitA(self, k)
  final def &&&[C](k: F[A, C]): F[A, (B, C)] = F.combine(self, k)
  ...
}

Let’s read Haskell’s Arrow tutorial:

(***) combines two arrows into a new arrow by running the two arrows on a pair of values (one arrow on the first item of the pair and one arrow on the second item of the pair).

Here’s an example:

scala> (f *** g)(1, 2)
res3: (Int, Int) = (2,200)

(&&&) combines two arrows into a new arrow by running the two arrows on the same value:

Here’s an example for &&&:

scala> (f &&& g)(2)
res4: (Int, Int) = (3,200)

Arrows I think can be useful if you need to add some context to functions and pairs.

Unapply 

One thing that I’ve been fighting the Scala compiler over is the lack of type inference support across the different kinded types like F[M[_, _]] and F[M[_]], and M[_] and F[M[_]].

For example, an instance of Applicative[M[_]] is (* -> *) -> * (a type constructor that takes another type constructor that that takes exactly one type). It’s known that Int => Int can be treated as an applicative by treating it as Int => A:

scala> Applicative[Function1[Int, Int]]
<console>:14: error: Int => Int takes no type parameters, expected: one
              Applicative[Function1[Int, Int]]
                          ^

scala> Applicative[({type l[A]=Function1[Int, A]})#l]
res14: scalaz.Applicative[[A]Int => A] = scalaz.std.FunctionInstances$$anon$2@56ae78ac

This becomes annoying for M[_,_] like Validation. One of the way Scalaz helps you out is to provide meta-instances of typeclass instance called Unapply.

trait Unapply[TC[_[_]], MA] {
  /** The type constructor */
  type M[_]
  /** The type that `M` was applied to */
  type A
  /** The instance of the type class */
  def TC: TC[M]
  /** Evidence that MA =:= M[A] */
  def apply(ma: MA): M[A]
}

When Scalaz method like traverse requires you to pass in Applicative[M[_]], it instead could ask for Unapply[Applicative, X]. During compile time, Scalac can look through all the implicit converters to see if it can coerce Function1[Int, Int] into M[A] by fixing or adding a parameter and of course using an existing typeclass instance.

scala> implicitly[Unapply[Applicative, Function1[Int, Int]]]
res15: scalaz.Unapply[scalaz.Applicative,Int => Int] = scalaz.Unapply_0$$anon$9@2e86566f

The feature I added yesterday allows type A to be promoted as M[A] by adding a fake type constructor. This let us treat Int as Applicative easier. But because it still requires TC0: TC[({type λ[α] = A0})#λ] implicitly, it does not allow just any type to be promoted as Applicative.

scala> implicitly[Unapply[Applicative, Int]]
res0: scalaz.Unapply[scalaz.Applicative,Int] = scalaz.Unapply_3$$anon$1@5179dc20

scala> implicitly[Unapply[Applicative, Any]]
<console>:14: error: Unable to unapply type `Any` into a type constructor of kind `M[_]` that is classified by the type class `scalaz.Applicative`
1) Check that the type class is defined by compiling `implicitly[scalaz.Applicative[<type constructor>]]`.
2) Review the implicits in object Unapply, which only cover common type 'shapes'
(implicit not found: scalaz.Unapply[scalaz.Applicative, Any])
              implicitly[Unapply[Applicative, Any]]
                        ^

Works. The upshot of all this is that we can now rewrite the following a bit cleaner:

scala> val failedTree: Tree[Validation[String, Int]] = 1.success[String].node(
         2.success[String].leaf, "boom".failure[Int].leaf)
failedTree: scalaz.Tree[scalaz.Validation[String,Int]] = <tree>

scala> failedTree.sequence[({type l[X]=Validation[String, X]})#l, Int]
res2: scalaz.Validation[java.lang.String,scalaz.Tree[Int]] = Failure(boom)

Here’s sequenceU:

scala> failedTree.sequenceU
res3: scalaz.Validation[String,scalaz.Tree[Int]] = Failure(boom)

Boom.

parallel composition 

With the change I made to Unapply monoidal applicative functor now works, but we still could not combine them:

scala> val f = { (x: Int) => x + 1 }
f: Int => Int = <function1>

scala> val g = { (x: Int) => List(x, 5) }
g: Int => List[Int] = <function1>

scala> val h = f &&& g
h: Int => (Int, List[Int]) = <function1>

scala> List(1, 2, 3) traverseU f
res0: Int = 9

scala> List(1, 2, 3) traverseU g
res1: List[List[Int]] = List(List(1, 2, 3), List(1, 2, 5), List(1, 5, 3), List(1, 5, 5), List(5, 2, 3), List(5, 2, 5), List(5, 5, 3), List(5, 5, 5))

scala> List(1, 2, 3) traverseU h
res2: (Int, List[List[Int]]) = (9,List(List(1, 5), List(2, 5), List(3, 5)))

Running f and g is working fine. The problem is the way pair is interpretted by traverseU. If I manually combined f and g, it would look like:

scala> val h = { (x: Int) => (f(x), g(x)) }
h: Int => (Int, List[Int]) = <function1>

And here is Tuple2Functor:

private[scalaz] trait Tuple2Functor[A1] extends Functor[({type f[x] = (A1, x)})#f] {
  override def map[A, B](fa: (A1, A))(f: A => B) =
    (fa._1, f(fa._2))
}

Scalaz does have a concept of product of applicative functors, which is available via product method available on Apply typeclass, however I don’t think it’s available as implicits because it’s using pairs to encode it. At this point I am not sure if Scalaz has a way to implementing product of applicative functions (A => M[B]) as described in EIP:

data (m ⊠ n) a = Prod {pfst ::m a,psnd :: n a}
(⊗)::(Functor m,Functor n) ⇒ (a → m b) → (a → n b) → (a → (m ⊠ n) b)
(f ⊗ g) x = Prod (f x) (g x)

This could also be true for composition too. Let’s branch from scalaz-seven branch:

$ git co scalaz-seven
Already on 'scalaz-seven'
$ git branch topic/appcompose
$ git co topic/appcompose
Switched to branch 'topic/appcompose'

We’ll first store things into an actual type and then worry about making it elegant later.

package scalaz

import Id._

trait XProduct[A, B] {
  def _1: A
  def _2: B
  override def toString: String = "XProduct(" + _1.toString + ", " + _2.toString + ")"
}

trait XProductInstances {
  implicit def productSemigroup[A1, A2](implicit A1: Semigroup[A1], A2: Semigroup[A2]): Semigroup[XProduct[A1, A2]] = new XProductSemigroup[A1, A2] {
    implicit def A1 = A1
    implicit def A2 = A2
  }  
  implicit def productFunctor[F[_], G[_]](implicit F0: Functor[F], G0: Functor[G]): Functor[({type λ[α] = XProduct[F[α], G[α]]})#λ] = new XProductFunctor[F, G] {
    def F = F0
    def G = G0
  }
  implicit def productPointed[F[_], G[_]](implicit F0: Pointed[F], G0: Pointed[G]): Pointed[({type λ[α] = XProduct[F[α], G[α]]})#λ] = new XProductPointed[F, G] {
    def F = F0
    def G = G0
  }
  implicit def productApply[F[_], G[_]](implicit F0: Apply[F], G0: Apply[G]): Apply[({type λ[α] = XProduct[F[α], G[α]]})#λ] = new XProductApply[F, G] {
    def F = F0
    def G = G0
  }
  implicit def productApplicativeFG[F[_], G[_]](implicit F0: Applicative[F], G0: Applicative[G]): Applicative[({type λ[α] = XProduct[F[α], G[α]]})#λ] = new XProductApplicative[F, G] {
    def F = F0
    def G = G0
  }
  implicit def productApplicativeFB[F[_], B](implicit F0: Applicative[F], B0: Applicative[({type λ[α] = B})#λ]): Applicative[({type λ[α] = XProduct[F[α], B]})#λ] = new XProductApplicative[F, ({type λ[α] = B})#λ] {
    def F = F0
    def G = B0
  }
  implicit def productApplicativeAG[A, G[_]](implicit A0: Applicative[({type λ[α] = A})#λ], G0: Applicative[G]): Applicative[({type λ[α] = XProduct[A, G[α]]})#λ] = new XProductApplicative[({type λ[α] = A})#λ, G] {
    def F = A0
    def G = G0
  }
  implicit def productApplicativeAB[A, B](implicit A0: Applicative[({type λ[α] = A})#λ], B0: Applicative[({type λ[α] = B})#λ]): Applicative[({type λ[α] = XProduct[A, B]})#λ] = new XProductApplicative[({type λ[α] = A})#λ, ({type λ[α] = B})#λ] {
    def F = A0
    def G = B0
  }  
}

trait XProductFunctions {
  def product[A, B](a1: A, a2: B): XProduct[A, B] = new XProduct[A, B] {
    def _1 = a1
    def _2 = a2
  }
}

object XProduct extends XProductFunctions with XProductInstances {
  def apply[A, B](a1: A, a2: B): XProduct[A, B] = product(a1, a2)
}
private[scalaz] trait XProductSemigroup[A1, A2] extends Semigroup[XProduct[A1, A2]] {
  implicit def A1: Semigroup[A1]
  implicit def A2: Semigroup[A2]
  def append(f1: XProduct[A1, A2], f2: => XProduct[A1, A2]) = XProduct(
    A1.append(f1._1, f2._1),
    A2.append(f1._2, f2._2)
    )
}
private[scalaz] trait XProductFunctor[F[_], G[_]] extends Functor[({type λ[α] = XProduct[F[α], G[α]]})#λ] {
  implicit def F: Functor[F]
  implicit def G: Functor[G]
  override def map[A, B](fa: XProduct[F[A], G[A]])(f: (A) => B): XProduct[F[B], G[B]] =
    XProduct(F.map(fa._1)(f), G.map(fa._2)(f))
}

private[scalaz] trait XProductPointed[F[_], G[_]] extends Pointed[({type λ[α] = XProduct[F[α], G[α]]})#λ] with XProductFunctor[F, G] {
  implicit def F: Pointed[F]
  implicit def G: Pointed[G]
  def point[A](a: => A): XProduct[F[A], G[A]] = XProduct(F.point(a), G.point(a))
}

private[scalaz] trait XProductApply[F[_], G[_]] extends Apply[({type λ[α] = XProduct[F[α], G[α]]})#λ] with XProductFunctor[F, G] {
  implicit def F: Apply[F]
  implicit def G: Apply[G]
  def ap[A, B](fa: => XProduct[F[A], G[A]])(f: => XProduct[F[A => B], G[A => B]]): XProduct[F[B], G[B]] =
    XProduct(F.ap(fa._1)(f._1), G.ap(fa._2)(f._2))
}

private[scalaz] trait XProductApplicative[F[_], G[_]] extends Applicative[({type λ[α] = XProduct[F[α], G[α]]})#λ] with XProductPointed[F, G] {
  implicit def F: Applicative[F]
  implicit def G: Applicative[G]
  def ap[A, B](fa: => XProduct[F[A], G[A]])(f: => XProduct[F[(A) => B], G[(A) => B]]): XProduct[F[B], G[B]] =
    XProduct(F.ap(fa._1)(f._1), G.ap(fa._2)(f._2))
}

The implementation is mostly ripped from Product.scala, which uses Tuple2. Here’s is the first attempt at using XProduct:

scala> XProduct(1.some, 2.some) map {_ + 1}
<console>:14: error: Unable to unapply type `scalaz.XProduct[Option[Int],Option[Int]]` into a type constructor of kind `M[_]` that is classified by the type class `scalaz.Functor`
1) Check that the type class is defined by compiling `implicitly[scalaz.Functor[<type constructor>]]`.
2) Review the implicits in object Unapply, which only cover common type 'shapes'
(implicit not found: scalaz.Unapply[scalaz.Functor, scalaz.XProduct[Option[Int],Option[Int]]])
              XProduct(1.some, 2.some) map {_ + 1}
                      ^

The error message is actually helpful if you know how to decode it. It’s looking for the Unapply meta-instance. Likely the particular shape is not there. Here’s the new unapply:

  implicit def unapplyMFGA[TC[_[_]], F[_], G[_], M0[_, _], A0](implicit TC0: TC[({type λ[α] = M0[F[α], G[α]]})#λ]): Unapply[TC, M0[F[A0], G[A0]]] {
    type M[X] = M0[F[X], G[X]]
    type A = A0
  } = new Unapply[TC, M0[F[A0], G[A0]]] {
    type M[X] = M0[F[X], G[X]]
    type A = A0
    def TC = TC0
    def apply(ma: M0[F[A0], G[A0]]) = ma
  }

Try again.

scala> XProduct(1.some, 2.some) map {_ + 1}
res0: scalaz.Unapply[scalaz.Functor,scalaz.XProduct[Option[Int],Option[Int]]]{type M[X] = scalaz.XProduct[Option[X],Option[X]]; type A = Int}#M[Int] = XProduct(Some(2), Some(3))

We can use it as normal applicative:

scala> (XProduct(1, 2.some) |@| XProduct(3, none[Int])) {_ |+| (_: XProduct[Int, Option[Int]]) }
res1: scalaz.Unapply[scalaz.Apply,scalaz.XProduct[Int,Option[Int]]]{type M[X] = scalaz.XProduct[Int,Option[Int]]; type A = scalaz.XProduct[Int,Option[Int]]}#M[scalaz.XProduct[Int,Option[Int]]] = XProduct(4, Some(2))

Let’s rewrite word count example from the EIP.

scala> val text = "the cat in the hat\n sat on the mat\n".toList
text: List[Char] = 
List(t, h, e,  , c, a, t,  , i, n,  , t, h, e,  , h, a, t, 
,  , s, a, t,  , o, n,  , t, h, e,  , m, a, t, 
)

scala> def count[A] = (a: A) => 1
count: [A]=> A => Int

scala> val charCount = count[Char]
charCount: Char => Int = <function1>

scala> text traverseU charCount
res10: Int = 35

scala> import scalaz.std.boolean.test
import scalaz.std.boolean.test

scala> val lineCount = (c: Char) => test(c === '\n')
lineCount: Char => Int = <function1>

scala> text traverseU lineCount
res11: Int = 2

scala> val wordCount = (c: Char) => for {
         x <- get[Boolean]
         val y = c =/= ' '
         _ <- put(y)
       } yield test(y /\ !x)
wordCount: Char => scalaz.StateT[scalaz.Id.Id,Int,Int] = <function1>

scala> (text traverseU wordCount) eval false count(_ > 0)
res25: Int = 9

scala> text traverseU { (c: Char) => XProduct(charCount(c), lineCount(c)) }
res26: scalaz.XProduct[Int,Int] = XProduct(35, 2)

Now it’s able to combine applicative functions in parallel. What happens if you use a pair?

scala> text traverseU { (c: Char) => (charCount(c), lineCount(c)) }
res27: (Int, List[Int]) = (35,List(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1))

Ha! However, the problem with Unapply is that it won’t work for more complex structure:

scala> text traverseU { (c: Char) => XProduct(charCount(c), wordCount(c)) }
<console>:19: error: Unable to unapply type `scalaz.XProduct[Int,scalaz.StateT[scalaz.Id.Id,Boolean,Int]]` into a type constructor of kind `M[_]` that is classified by the type class `scalaz.Applicative`
1) Check that the type class is defined by compiling `implicitly[scalaz.Applicative[<type constructor>]]`.
2) Review the implicits in object Unapply, which only cover common type 'shapes'
(implicit not found: scalaz.Unapply[scalaz.Applicative, scalaz.XProduct[Int,scalaz.StateT[scalaz.Id.Id,Boolean,Int]]])
              text traverseU { (c: Char) => XProduct(charCount(c), wordCount(c)) }
                   ^

Once it all works out, it would be cool to have @>>> and @&&& operator on Arrow or Function1 that does the applicative composition as it’s described in EIP.

We’ll cover some other topic later.

day 16 

Yesterday we looked at Arrow as a way of abstracting function-like things and Unapply as a way of providing typeclass meta-instances. We also continued on with the applicative experiment by implementing XProduct that supports parallel compositions.

Memo 

Pure functions don’t imply they are computationally cheap. For example, calculate a list of SHA-1 hash for all permutations of ASCII character string up to 8 characters length. If we don’t count the tab character there are 95 printable characters in ASCII, so let’s round that up to 100. 100 ^ 8 is 10 ^ 16. Even if we could handle 1000 hashing per second, it takes 10 ^ 13 secs, or 316888 years.

Given you have some space in RAM, we could trade some of the expensive calculations for space by caching the result. This is called memoization. Here’s the contract for Memo:

sealed trait Memo[@specialized(Int) K, @specialized(Int, Long, Double) V] {
  def apply(z: K => V): K => V
}

We pass in a potentially expensive function as an input and you get back a function that behaves the same but may cache the result. Under Memo object there are some default implementations of Memo like Memo.mutableHashMapMemo[K, V], Memo.weakHashMapMemo[K, V], and Memo.arrayMemo[V].

In general, we should be careful with any of these optimization techniques. First the overall performance should be profiled to see if it in fact would contribute to time savings, and second space trade-off needs to be analyzed so it doesn’t grow endlessly.

Let’s implement Fibonacci number example from the Memoization tutorial:

scala> val slowFib: Int => Int = {
         case 0 => 0
         case 1 => 1
         case n => slowFib(n - 2) + slowFib(n - 1)
       }
slowFib: Int => Int = <function1>

scala> slowFib(30)
res0: Int = 832040

scala> slowFib(40)
res1: Int = 102334155

scala> slowFib(45)
res2: Int = 1134903170

The slowFib(45) took a while to return. Now the memoized version:

scala> val memoizedFib: Int => Int = Memo.mutableHashMapMemo {
         case 0 => 0
         case 1 => 1
         case n => memoizedFib(n - 2) + memoizedFib(n - 1)
       }
memoizedFib: Int => Int = <function1>

scala> memoizedFib(30)
res12: Int = 832040

scala> memoizedFib(40)
res13: Int = 102334155

scala> memoizedFib(45)
res14: Int = 1134903170

Now these numbers come back instantaneously. The neat thing is that for both creating and using the memoized function, it feels very transparently done. Adam Rosien brings up that point in his Scalaz “For the Rest of Us” talk (video).

functional programming 

What is functional programming? Rúnar Óli defines it as:

programming with functions.

What’s a function?

f: A => B relates every value of type of A to excatly one value of type B and nothing else.

To clarify the “nothing else” part, he introduces the notion of referential transparency as follows:

An expression e is referentially transparent if every occurrence e can be replaced with its value without affecting the observable result of the program.

Using this notion, we can think of functional programming as building up referentially transparent expression tree. Memoization is one way of taking the advantage of referential transparency.

Effect system 

In Lazy Functional State Threads John Launchbury and Simon Peyton-Jones write:

Based on earlier work on monads, we present a way of securely encapsulating stateful computations that manipulate multiple, named, mutable objects, in the context of a non-strict purely-functional language.

Because Scala has var at first it seems like we might not need this, but the concept of encapsulating stateful computation can be useful. Under some circumstances like concurrently running computations, it’s critical that states are either not shared or shared carefully.

ST 

In Scalaz there’s ST monad that corresponds to ST described in the paper. Also see Towards an Effect System in Scala, Part 1: ST Monad by Rúnar for details. Here’s the typeclass contract for ST:

sealed trait ST[S, A] {
  private[effect] def apply(s: World[S]): (World[S], A)
}

This looks similar to State monad, but the difference I think is that the state is mutated in-place, and in return is not observable from outside.

STRef 

LFST:

What, then is a “state”? Part of every state is a finite mapping from reference to values. … A reference can be thought of as the name of (or address of) a variable, an updatable location in the state capable of holding a value.

STRef is a mutable variable that’s used only within the context of ST monad. It’s created using ST.newVar[A], and supports the following operations:

sealed trait STRef[S, A] {
  protected var value: A

  /**Reads the value pointed at by this reference. */
  def read: ST[S, A] = returnST(value)
  /**Modifies the value at this reference with the given function. */
  def mod[B](f: A => A): ST[S, STRef[S, A]] = ...
  /**Associates this reference with the given value. */
  def write(a: => A): ST[S, STRef[S, A]] = ...
  /**Synonym for write*/
  def |=(a: => A): ST[S, STRef[S, A]] = ...
  /**Swap the value at this reference with the value at another. */
  def swap(that: STRef[S, A]): ST[S, Unit] = ...
}

I’m going to use my local version of Scalaz 7:

$ sbt
scalaz> project effect
scalaz-effect> console
[info] Compiling 2 Scala sources to /Users/eed3si9n/work/scalaz-seven/effect/target/scala-2.9.2/classes...
[info] Starting scala interpreter...
[info]

scala> import scalaz._
import scalaz._

scala> import Scalaz._
import Scalaz._

scala> import effect._
import effect._

scala> import ST.{newVar, runST, newArr, returnST}
import ST.{newVar, runST, newArr, returnST}

scala> def e1[S] = for {
         x <- newVar[S](0)
         r <- x mod {_ + 1}
       } yield x
e1: [S]=> scalaz.effect.ST[S,scalaz.effect.STRef[S,Int]]

scala> def e2[S]: ST[S, Int] = for {
         x <- e1[S]
         r <- x.read
       } yield r
e2: [S]=> scalaz.effect.ST[S,Int]

scala> type ForallST[A] = Forall[({type λ[S] = ST[S, A]})#λ]
defined type alias ForallST

scala> runST(new ForallST[Int] { def apply[S] = e2[S] })
res5: Int = 1

On Rúnar’s blog, Paul Chiusano (@pchiusano) asks what you’re probably thinking:

I’m still sort of undecided on the utility of doing this in Scala – just to play devils advocate – if you need to do some local mutation for purposes of implementing an algorithm (like, say, quicksort), just don’t mutate anything passed into your function. Is there much benefit in convincing the compiler you’ve done this properly? I am not sure I care about having compiler help with this.

He comes back to the site 30 min later and answers himself:

If I were writing an imperative quicksort, I would probably copy the input sequence to an array, mutate it in place during the sort, then return some immutable view of the sorted array. With STRef, I can accept an STRef to a mutable array, and avoid making a copy at all. Furthermore, my imperative actions are first class and I can use all the usual combinators for combining them.

This is an interesting point. Because the mutable state is guaranteed not to bleed out, the change to the mutable state can be chained and composed without copying the data around. When you need mutation, many times you need arrays, so there’s an array wrapper called STArray:

sealed trait STArray[S, A] {
  val size: Int
  val z: A
  private val value: Array[A] = Array.fill(size)(z)
  /**Reads the value at the given index. */
  def read(i: Int): ST[S, A] = returnST(value(i))
  /**Writes the given value to the array, at the given offset. */
  def write(i: Int, a: A): ST[S, STArray[S, A]] = ...
  /**Turns a mutable array into an immutable one which is safe to return. */
  def freeze: ST[S, ImmutableArray[A]] = ...
  /**Fill this array from the given association list. */
  def fill[B](f: (A, B) => A, xs: Traversable[(Int, B)]): ST[S, Unit] = ...
  /**Combine the given value with the value at the given index, using the given function. */
  def update[B](f: (A, B) => A, i: Int, v: B) = ...
}

This is created using ST.newArr(size: Int, z: A). Let’s calculate all the prime numbers including or under 1000 using the sieve of Eratosthenes..

Interruption 

I actually found a bug in STArray implementation. Let me fix this up quickly.

$ git pull --rebase
Current branch scalaz-seven is up to date.
$ git branch topic/starrayfix
$ git co topic/starrayfix
Switched to branch 'topic/starrayfix'

Since ST is missing a spec, I’m going to start one to reproduce the bug. This way it would be caught if someone tried to roll back my fix.

package scalaz
package effect

import std.AllInstances._
import ST._

class STTest extends Spec {
  type ForallST[A] = Forall[({type λ[S] = ST[S, A]})#λ]

  "STRef" in {
    def e1[S] = for {
      x <- newVar[S](0)
      r <- x mod {_ + 1}
    } yield x
    def e2[S]: ST[S, Int] = for {
      x <- e1[S]
      r <- x.read
    } yield r
    runST(new ForallST[Int] { def apply[S] = e2[S] }) must be_===(1)
  }

  "STArray" in {
    def e1[S] = for {
      arr <- newArr[S, Boolean](3, true)
      _ <- arr.write(0, false)
      r <- arr.freeze
    } yield r
    runST(new ForallST[ImmutableArray[Boolean]] { def apply[S] = e1[S] }).toList must be_===(
      List(false, true, true))
  }
}

Here’s the result:

[info] STTest
[info]
[info] + STRef
[error] ! STArray
[error]   NullPointerException: null (ArrayBuilder.scala:37)
[error] scala.collection.mutable.ArrayBuilder$.make(ArrayBuilder.scala:37)
[error] scala.Array$.newBuilder(Array.scala:52)
[error] scala.Array$.fill(Array.scala:235)
[error] scalaz.effect.STArray$class.$init$(ST.scala:71)
...

NullPointerException in Scala?! This is coming from the following code in STArray:

sealed trait STArray[S, A] {
  val size: Int
  val z: A
  implicit val manifest: Manifest[A]

  private val value: Array[A] = Array.fill(size)(z)
  ...
}
...
trait STArrayFunctions {
  def stArray[S, A](s: Int, a: A)(implicit m: Manifest[A]): STArray[S, A] = new STArray[S, A] {
    val size = s
    val z = a
    implicit val manifest = m
  }
}

Do you see it? Paulp wrote a FAQ on this. value is initialized using uninitialized size and z. Here’s my fix:

sealed trait STArray[S, A] {
  def size: Int
  def z: A
  implicit def manifest: Manifest[A]

  private lazy val value: Array[A] = Array.fill(size)(z)
  ...
}

Now the test passes. Push it up and send a pull request.

Back to the usual programming 

The sieve of Eratosthenes is a simple algorithm to calculate prime numbers.

scala> import scalaz._, Scalaz._, effect._, ST._
import scalaz._
import Scalaz._
import effect._
import ST._

scala> def mapM[A, S, B](xs: List[A])(f: A => ST[S, B]): ST[S, List[B]] =
         Monad[({type λ[α] = ST[S, α]})#λ].sequence(xs map f)
mapM: [A, S, B](xs: List[A])(f: A => scalaz.effect.ST[S,B])scalaz.effect.ST[S,List[B]]

scala> def sieve[S](n: Int) = for {
         arr <- newArr[S, Boolean](n + 1, true)
         _ <- arr.write(0, false)
         _ <- arr.write(1, false)
         val nsq = (math.sqrt(n.toDouble).toInt + 1)
         _ <- mapM (1 |-> nsq) { i =>
           for {
             x <- arr.read(i)
             _ <-
               if (x) mapM (i * i |--> (i, n)) { j => arr.write(j, false) }
               else returnST[S, List[Boolean]] {Nil}
           } yield ()
         }
         r <- arr.freeze
       } yield r
sieve: [S](n: Int)scalaz.effect.ST[S,scalaz.ImmutableArray[Boolean]]

scala> type ForallST[A] = Forall[({type λ[S] = ST[S, A]})#λ]
defined type alias ForallST

scala> def prime(n: Int) =
         runST(new ForallST[ImmutableArray[Boolean]] { def apply[S] = sieve[S](n) }).toArray.
         zipWithIndex collect { case (true, x) => x }
prime: (n: Int)Array[Int]

scala> prime(1000)
res21: Array[Int] = Array(2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, ...

The result looks ok according this list of first 1000 primes. The most difficult part was wrapping my head around the iteration over STArray. Because we are in the context of ST[S, _], the result of the loop also needs to be an ST monad. If we mapped over a list and wrote into the array that’s going to return List[ST[S, Unit]].

I implemented mapM, which takes a monadic function for ST[S, B] and returns ST[S, List[B]] by inverting the monads. It’s basically like sequence, but I think it’s easier to understand. It’s definitely not pain-free compared to using var, but the ability to pass around the mutable contexts around may be useful.

We’ll pick it from from here later.

day 17 

Yesterday we looked at Memo for caching computation results, and ST as a way of encapsulating mutation. Today we’ll continue into IO.

Daniel Steger for openphoto.net

IO Monad 

Instead of reading the second half of the paper, we can get the gist by reading Towards an Effect System in Scala, Part 2: IO Monad by Rúnar (@runarorama):

While ST gives us guarantees that mutable memory is never shared, it says nothing about reading/writing files, throwing exceptions, opening network sockets, database connections, etc.

Here’s the typeclass contract for ST again:

sealed trait ST[S, A] {
  private[effect] def apply(s: World[S]): (World[S], A)
}

And the following is the typeclass contract of IO:

sealed trait IO[+A] {
  private[effect] def apply(rw: World[RealWorld]): Trampoline[(World[RealWorld], A)]
}

If we ignore the Trampoline part, IO is like ST with state fixed to RealWorld. Similar to ST, we can create IO monads using the functions under IO object. Here’s Hello world.

scala> import scalaz._, Scalaz._, effect._, IO._
import scalaz._
import Scalaz._
import effect._
import IO._

scala> val action1 = for {
         _ <- putStrLn("Hello, world!")
       } yield ()
action1: scalaz.effect.IO[Unit] = scalaz.effect.IOFunctions$$anon$4@149f6f65

scala> action1.unsafePerformIO
Hello, world!

Here are the IO actions under IO:

  /** Reads a character from standard input. */
  def getChar: IO[Char] = ...
  /** Writes a character to standard output. */
  def putChar(c: Char): IO[Unit] = ...
  /** Writes a string to standard output. */
  def putStr(s: String): IO[Unit] = ...
  /** Writes a string to standard output, followed by a newline.*/
  def putStrLn(s: String): IO[Unit] = ...
  /** Reads a line of standard input. */
  def readLn: IO[String] = ...
  /** Write the given value to standard output. */
  def putOut[A](a: A): IO[Unit] = ...
  // Mutable variables in the IO monad
  def newIORef[A](a: => A): IO[IORef[A]] = ...
  /**Throw the given error in the IO monad. */
  def throwIO[A](e: Throwable): IO[A] = ...
  /** An IO action that does nothing. */
  val ioUnit: IO[Unit] = ...
}

We can also make our own action using the apply method under IO object as follows:

scala> val action2 = IO {
         val source = scala.io.Source.fromFile("./README.md")
         source.getLines.toStream
       }
action2: scalaz.effect.IO[scala.collection.immutable.Stream[String]] = scalaz.effect.IOFunctions$$anon$4@bab4387

scala> action2.unsafePerformIO.toList
res57: List[String] = List(# Scalaz, "", Scalaz is a Scala library for functional programming., "", It provides purely functional data structures to complement those from the Scala standard library., ...

TESS2:

Composing these into programs is done monadically. So we can use for-comprehensions. Here’s a program that reads a line of input and prints it out again:

def program: IO[Unit] = for {
  line <- readLn
  _    <- putStrLn(line)
} yield ()

IO[Unit] is an instance of Monoid, so we can re-use the monoid addition function |+|.

Let’s try this out:

scala> (program |+| program).unsafePerformIO
123
123

Enumeration-Based I/O with Iteratees 

There’s another way of handling IOs called Iteratee that is talk of the town. There’s Scalaz Tutorial: Enumeration-Based I/O with Iteratees (EBIOI) by Rúnar on Scalaz 5 implementation, but a whole new Iteratee has been added to Scalaz 7.

I am going to read EBIOI first:

Most programmers have come across the problem of treating an I/O data source (such as a file or a socket) as a data structure. This is a common thing to want to do. … Instead of implementing an interface from which we request Strings by pulling, we’re going to give an implementation of an interface that can receive Strings by pushing. And indeed, this idea is nothing new. This is exactly what we do when we fold a list:

def foldLeft[B](b: B)(f: (B, A) => B): B

Let’s look at Scalaz 7’s interfaces. Here’s Input:

sealed trait Input[E] {
  def fold[Z](empty: => Z, el: (=> E) => Z, eof: => Z): Z
  def apply[Z](empty: => Z, el: (=> E) => Z, eof: => Z) =
    fold(empty, el, eof)
}

And here’s IterateeT:

sealed trait IterateeT[E, F[_], A] {
  def value: F[StepT[E, F, A]]
}
type Iteratee[E, A] = IterateeT[E, Id, A]

object Iteratee
  extends IterateeFunctions
  with IterateeTFunctions
  with EnumeratorTFunctions
  with EnumeratorPFunctions
  with EnumerateeTFunctions
  with StepTFunctions
  with InputFunctions {

  def apply[E, A](s: Step[E, A]): Iteratee[E, A] = iteratee(s)
}

type >@>[E, A] = Iteratee[E, A]

IterateeT seems to be a monad transformer.

EBIOI:

Let’s see how we would use this to process a List. The following function takes a list and an iteratee and feeds the list’s elements to the iteratee.

We can skip this step, because Iteratee object extends EnumeratorTFunctions, which implements enumerate etc:

  def enumerate[E](as: Stream[E]): Enumerator[E] = ...
  def enumList[E, F[_] : Monad](xs: List[E]): EnumeratorT[E, F] = ...
  ...

This returns Enumerator[E], which is defined as follows:

trait EnumeratorT[E, F[_]] { self =>
  def apply[A]: StepT[E, F, A] => IterateeT[E, F, A]
  ...
}
type Enumerator[E] = EnumeratorT[E, Id]

Let’s try implementing the counter example from EBIOI. For that we switch to iteratee project using sbt:

$ sbt
scalaz> project iteratee
scalaz-iteratee> console
[info] Starting scala interpreter...

scala> import scalaz._, Scalaz._, iteratee._, Iteratee._
import scalaz._
import Scalaz._
import iteratee._
import Iteratee._

scala> def counter[E]: Iteratee[E, Int] = {
         def step(acc: Int)(s: Input[E]): Iteratee[E, Int] =
           s(el = e => cont(step(acc + 1)),
             empty = cont(step(acc)),
             eof = done(acc, eofInput[E])
           )
         cont(step(0))
       }
counter: [E]=> scalaz.iteratee.package.Iteratee[E,Int]

scala> (counter[Int] &= enumerate(Stream(1, 2, 3))).run
res0: scalaz.Id.Id[Int] = 3

For common operation like this, Scalaz provides these folding functions under Iteratee object. But because it was written for IterateeT in mind, we need to supply Id monad as a type parameter:

scala> (length[Int, Id] &= enumerate(Stream(1, 2, 3))).run
res1: scalaz.Scalaz.Id[Int] = 3

I’ll just copy the drop and head from IterateeTFunctions:

  /**An iteratee that skips the first n elements of the input **/
  def drop[E, F[_] : Pointed](n: Int): IterateeT[E, F, Unit] = {
    def step(s: Input[E]): IterateeT[E, F, Unit] =
      s(el = _ => drop(n - 1),
        empty = cont(step),
        eof = done((), eofInput[E]))
    if (n == 0) done((), emptyInput[E])
    else cont(step)
  }

  /**An iteratee that consumes the head of the input **/
  def head[E, F[_] : Pointed]: IterateeT[E, F, Option[E]] = {
    def step(s: Input[E]): IterateeT[E, F, Option[E]] =
      s(el = e => done(Some(e), emptyInput[E]),
        empty = cont(step),
        eof = done(None, eofInput[E])
      )
    cont(step)
  }

Composing Iteratees 

EBIOI:

In other words, iteratees compose sequentially.

Here’s drop1keep1 using Scalaz 7:

scala> def drop1Keep1[E]: Iteratee[E, Option[E]] = for {
         _ <- drop[E, Id](1)
         x <- head[E, Id]
       } yield x
drop1Keep1: [E]=> scalaz.iteratee.package.Iteratee[E,Option[E]]

There’s now repeatBuild function that can accumulate to a given monoid, so we can write Stream version of alternates example as follows:

scala> def alternates[E]: Iteratee[E, Stream[E]] =
         repeatBuild[E, Option[E], Stream](drop1Keep1) map {_.flatten}
alternates: [E](n: Int)scalaz.iteratee.package.Iteratee[E,Stream[E]]

scala> (alternates[Int] &= enumerate(Stream.range(1, 15))).run.force
res7: scala.collection.immutable.Stream[Int] = Stream(2, 4, 6, 8, 10, 12, 14)

File Input With Iteratees 

EBIOI:

Using the iteratees to read from file input turns out to be incredibly easy.

To process java.io.Reader Scalaz 7 comes with Iteratee.enumReader[F[_]](r: => java.io.Reader) function. This is when it starts to make sense why Iteratee was implemented as IterateeT because we can just stick IO into it:

scala> import scalaz._, Scalaz._, iteratee._, Iteratee._, effect._
import scalaz._
import Scalaz._
import iteratee._
import Iteratee._
import effect._

scala> import java.io._
import java.io._

scala> enumReader[IO](new BufferedReader(new FileReader("./README.md")))
res0: scalaz.iteratee.EnumeratorT[scalaz.effect.IoExceptionOr[Char],scalaz.effect.IO] = scalaz.iteratee.EnumeratorTFunctions$$anon$14@548ace66

To get the first character, we can run head[Char, IO] as follows:

scala> (head[IoExceptionOr[Char], IO] &= res0).map(_ flatMap {_.toOption}).run.unsafePerformIO
res1: Option[Char] = Some(#)

EBIOI:

We can get the number of lines in two files combined, by composing two enumerations and using our “counter” iteratee from above.

Let’s try this out.

scala> def lengthOfTwoFiles(f1: File, f2: File) = {
         val l1 = length[IoExceptionOr[Char], IO] &= enumReader[IO](new BufferedReader(new FileReader(f1)))
         val l2 = l1 &= enumReader[IO](new BufferedReader(new FileReader(f2)))
         l2.run
       }

scala> lengthOfTwoFiles(new File("./README.md"), new File("./TODO.txt")).unsafePerformIO
res65: Int = 12731

There are some more interesting examples in IterateeUsage.scala:

scala> val readLn = takeWhile[Char, List](_ != '\n') flatMap (ln => drop[Char, Id](1).map(_ => ln))
readLn: scalaz.iteratee.IterateeT[Char,scalaz.Id.Id,List[Char]] = scalaz.iteratee.IterateeTFunctions$$anon$9@560ff23d

scala> (readLn &= enumStream("Iteratees\nare\ncomposable".toStream)).run
res67: scalaz.Id.Id[List[Char]] = List(I, t, e, r, a, t, e, e, s)

scala> (collect[List[Char], List] %= readLn.sequenceI &= enumStream("Iteratees\nare\ncomposable".toStream)).run
res68: scalaz.Id.Id[List[List[Char]]] = List(List(I, t, e, r, a, t, e, e, s), List(a, r, e), List(c, o, m, p, o, s, a, b, l, e))

In the above sequenceI method turns readLn into an EnumerateeT, and %= is able to chain it to an iteratee.

EBIOI:

So what we have here is a uniform and compositional interface for enumerating both pure and effectful data sources.

It might take a while for this one to sink in.

Links 

• Scalaz Tutorial: Enumeration-Based I/O with Iteratees
• Iteratees. This is Josh Suereth (@jsuereth)’s take on Iteratees.
• Enumerator and iteratee from Haskell wiki.

day 18 

On day 17 we looked at IO monad as a way of abstracting side effects, and Iteratees as a way of handling streams. And the series ended.

Func 

I wanted to continue exploring a better way to compose applicative functions, and came up with a wrapper called AppFunc:

val f = AppFuncU { (x: Int) => x + 1 }
val g = AppFuncU { (x: Int) => List(x, 5) }
(f @&&& g) traverse List(1, 2, 3)

After sending this in as a pull request Lars Hupel (@larsr_h) suggested that I generalize the concept using typelevel module, so I expanded it to Func:

/**
 * Represents a function `A => F[B]` where `[F: TC]`.
 */
trait Func[F[_], TC[F[_]] <: Functor[F], A, B] {
  def runA(a: A): F[B]
  implicit def TC: KTypeClass[TC]
  implicit def F: TC[F]
  ...
}

Using this, AppFunc becomes Func with Applicative in the second type parameter. Lars still wants to expand it composition into general HList, but I am optimistic that this will be part of Scalaz 7 eventually.

I’ve updated this post quite a bit based on the guidance by Rúnar. See source in github for older revisions.

Free Monad 

What I want to explore today actually is the Free monad by reading Gabriel Gonzalez’s Why free monads matter:

Let’s try to come up with some sort of abstraction that represents the essence of a syntax tree. … Our toy language will only have three commands:

output b -- prints a "b" to the console
bell     -- rings the computer's bell
done     -- end of execution

So we represent it as a syntax tree where subsequent commands are leaves of prior commands:

data Toy b next =
    Output b next
  | Bell next
  | Done

Here’s Toy translated into Scala as is:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait Toy[+A, +Next]
case class Output[A, Next](a: A, next: Next) extends Toy[A, Next]
case class Bell[Next](next: Next) extends Toy[Nothing, Next]
case class Done() extends Toy[Nothing, Nothing]

// Exiting paste mode, now interpreting.

scala> Output('A', Done())
res0: Output[Char,Done] = Output(A,Done())

scala> Bell(Output('A', Done()))
res1: Bell[Output[Char,Done]] = Bell(Output(A,Done()))

CharToy 

WFMM’s DSL takes the type of output data as one of the type parameters, so it’s able to handle any output types. As demonstrated above as Toy, Scala can do this too. But doing so unnecessarily complicates the demonstration of of Free because of Scala’s handling of partially applied types. So we’ll first hardcode the data type to Char as follows:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait CharToy[+Next]
object CharToy {
  case class CharOutput[Next](a: Char, next: Next) extends CharToy[Next]
  case class CharBell[Next](next: Next) extends CharToy[Next]
  case class CharDone() extends CharToy[Nothing]

  def output[Next](a: Char, next: Next): CharToy[Next] = CharOutput(a, next)
  def bell[Next](next: Next): CharToy[Next] = CharBell(next)
  def done: CharToy[Nothing] = CharDone()
}

// Exiting paste mode, now interpreting.

scala> import CharToy._
import CharToy._

scala> output('A', done)
res0: CharToy[CharToy[Nothing]] = CharOutput(A,CharDone())

scala> bell(output('A', done))
res1: CharToy[CharToy[CharToy[Nothing]]] = CharBell(CharOutput(A,CharDone()))

I’ve added helper functions lowercase output, bell, and done to unify the types to CharToy.

Fix 

WFMM:

but unfortunately this doesn’t work because every time I want to add a command, it changes the type.

Let’s define Fix:

scala> :paste
// Entering paste mode (ctrl-D to finish)

case class Fix[F[_]](f: F[Fix[F]])
object Fix {
  def fix(toy: CharToy[Fix[CharToy]]) = Fix[CharToy](toy)
}

// Exiting paste mode, now interpreting.

scala> import Fix._
import Fix._

scala> fix(output('A', fix(done)))
res4: Fix[CharToy] = Fix(CharOutput(A,Fix(CharDone())))

scala> fix(bell(fix(output('A', fix(done)))))
res5: Fix[CharToy] = Fix(CharBell(Fix(CharOutput(A,Fix(CharDone())))))

Again, fix is provided so that the type inference works.

FixE 

We are also going to try to implement FixE, which adds exception to this. Since throw and catch are reserverd, I am renaming them to throwy and catchy:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait FixE[F[_], E]
object FixE {
  case class Fix[F[_], E](f: F[FixE[F, E]]) extends FixE[F, E]
  case class Throwy[F[_], E](e: E) extends FixE[F, E]

  def fix[E](toy: CharToy[FixE[CharToy, E]]): FixE[CharToy, E] =
  　　Fix[CharToy, E](toy)
  def throwy[F[_], E](e: E): FixE[F, E] = Throwy(e)
  def catchy[F[_]: Functor, E1, E2](ex: => FixE[F, E1])
  　　(f: E1 => FixE[F, E2]): FixE[F, E2] = ex match {
    case Fix(x)    => Fix[F, E2](Functor[F].map(x) {catchy(_)(f)})
    case Throwy(e) => f(e)
  }
}

// Exiting paste mode, now interpreting.

We can only use this if Toy b is a functor, so we muddle around until we find something that type-checks (and satisfies the Functor laws).

Let’s define Functor for CharToy:

scala> implicit val charToyFunctor: Functor[CharToy] = new Functor[CharToy] {
         def map[A, B](fa: CharToy[A])(f: A => B): CharToy[B] = fa match {
           case o: CharOutput[A] => CharOutput(o.a, f(o.next))
           case b: CharBell[A]   => CharBell(f(b.next))
           case CharDone()       => CharDone()
         }
       }
charToyFunctor: scalaz.Functor[CharToy] = $anon$1@7bc135fe

Here’s the sample usage:

scala> :paste
// Entering paste mode (ctrl-D to finish)

import FixE._
case class IncompleteException()
def subroutine = fix[IncompleteException](
  output('A',
    throwy[CharToy, IncompleteException](IncompleteException())))
def program = catchy[CharToy, IncompleteException, Nothing](subroutine) { _ =>
  fix[Nothing](bell(fix[Nothing](done)))
}

The fact that we need to supply type parameters everywhere is a bit unfortunate.

Free monads part 1 

WFMM:

our FixE already exists, too, and it’s called the Free monad:

data Free f r = Free (f (Free f r)) | Pure r

As the name suggests, it is automatically a monad (if f is a functor):

instance (Functor f) => Monad (Free f) where
    return = Pure
    (Free x) >>= f = Free (fmap (>>= f) x)
    (Pure r) >>= f = f r

The return was our Throw, and (>>=) was our catch.

The corresponding structure in Scalaz is called Free:

sealed abstract class Free[S[+_], +A](implicit S: Functor[S]) {
  final def map[B](f: A => B): Free[S, B] =
    flatMap(a => Return(f(a)))

  final def flatMap[B](f: A => Free[S, B]): Free[S, B] = this match {
    case Gosub(a, g) => Gosub(a, (x: Any) => Gosub(g(x), f))
    case a           => Gosub(a, f)
  }
  ...
}

object Free extends FreeInstances {
  /** Return from the computation with the given value. */
  case class Return[S[+_]: Functor, +A](a: A) extends Free[S, A]

  /** Suspend the computation with the given suspension. */
  case class Suspend[S[+_]: Functor, +A](a: S[Free[S, A]]) extends Free[S, A]

  /** Call a subroutine and continue with the given function. */
  case class Gosub[S[+_]: Functor, A, +B](a: Free[S, A],
                                          f: A => Free[S, B]) extends Free[S, B]
}

trait FreeInstances {
  implicit def freeMonad[S[+_]:Functor]: Monad[({type f[x] = Free[S, x]})#f] =
    new Monad[({type f[x] = Free[S, x]})#f] {
      def point[A](a: => A) = Return(a)
      override def map[A, B](fa: Free[S, A])(f: A => B) = fa map f
      def bind[A, B](a: Free[S, A])(f: A => Free[S, B]) = a flatMap f
    }
}

In Scalaz version, Free constructor is called Free.Suspend and Pure is called Free.Return. Let’s re-implement CharToy commands based on Free:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait CharToy[+Next]
object CharToy {
  case class CharOutput[Next](a: Char, next: Next) extends CharToy[Next]
  case class CharBell[Next](next: Next) extends CharToy[Next]
  case class CharDone() extends CharToy[Nothing]

  implicit val charToyFunctor: Functor[CharToy] = new Functor[CharToy] {
    def map[A, B](fa: CharToy[A])(f: A => B): CharToy[B] = fa match {
        case o: CharOutput[A] => CharOutput(o.a, f(o.next))
        case b: CharBell[A]   => CharBell(f(b.next))
        case CharDone()       => CharDone()
      }
    }

  def output(a: Char): Free[CharToy, Unit] =
    Free.Suspend(CharOutput(a, Free.Return[CharToy, Unit](())))
  def bell: Free[CharToy, Unit] =
    Free.Suspend(CharBell(Free.Return[CharToy, Unit](())))
  def done: Free[CharToy, Unit] = Free.Suspend(CharDone())
}

// Exiting paste mode, now interpreting.

defined trait CharToy
defined module CharToy

I’ll be damned if that’s not a common pattern we can abstract.

Let’s add liftF refactoring. We also need a return equivalent, which we’ll call pointed.

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait CharToy[+Next]
object CharToy {
  case class CharOutput[Next](a: Char, next: Next) extends CharToy[Next]
  case class CharBell[Next](next: Next) extends CharToy[Next]
  case class CharDone() extends CharToy[Nothing]

  implicit val charToyFunctor: Functor[CharToy] = new Functor[CharToy] {
    def map[A, B](fa: CharToy[A])(f: A => B): CharToy[B] = fa match {
        case o: CharOutput[A] => CharOutput(o.a, f(o.next))
        case b: CharBell[A]   => CharBell(f(b.next))
        case CharDone()       => CharDone()
      }
    }
  private def liftF[F[+_]: Functor, R](command: F[R]): Free[F, R] =
    Free.Suspend[F, R](Functor[F].map(command) { Free.Return[F, R](_) })
  def output(a: Char): Free[CharToy, Unit] =
    liftF[CharToy, Unit](CharOutput(a, ()))
  def bell: Free[CharToy, Unit] = liftF[CharToy, Unit](CharBell(()))
  def done: Free[CharToy, Unit] = liftF[CharToy, Unit](CharDone())
  def pointed[A](a: A) = Free.Return[CharToy, A](a)
}

// Exiting paste mode, now interpreting.

Here’s the command sequence:

scala> import CharToy._
import CharToy._

scala> val subroutine = output('A')
subroutine: scalaz.Free[CharToy,Unit] = Suspend(CharOutput(A,Return(())))

scala> val program = for {
         _ <- subroutine
         _ <- bell
         _ <- done
       } yield ()
program: scalaz.Free[CharToy,Unit] = Gosub(<function0>,<function1>)

This is where things get magical. We now have do notation for something that hasn’t even been interpreted yet: it’s pure data.

Next we’d like to define showProgram to prove that what we have is just data. WFMM defines showProgram using simple pattern matching, but it doesn’t quite work that way for our Free. See the definition of flatMap:

  final def flatMap[B](f: A => Free[S, B]): Free[S, B] = this match {
    case Gosub(a, g) => Gosub(a, (x: Any) => Gosub(g(x), f))
    case a           => Gosub(a, f)
  }

Instead of recalculating a new Return or Suspend it’s just creating Gosub structure. There’s resume method that evaluates Gosub and returns \/, so using that we can implement showProgram as:

scala> def showProgram[R: Show](p: Free[CharToy, R]): String =
         p.resume.fold({
           case CharOutput(a, next) =>
             "output " + Show[Char].shows(a) + "\n" + showProgram(next)
           case CharBell(next) =>
             "bell " + "\n" + showProgram(next)
           case CharDone() =>
             "done\n"
         },
         { r: R => "return " + Show[R].shows(r) + "\n" })
showProgram: [R](p: scalaz.Free[CharToy,R])(implicit evidence$1: scalaz.Show[R])String

scala> showProgram(program)
res12: String =
"output A
bell
done
"

Here’s the pretty printer:

scala> def pretty[R: Show](p: Free[CharToy, R]) = print(showProgram(p))
pretty: [R](p: scalaz.Free[CharToy,R])(implicit evidence$1: scalaz.Show[R])Unit

scala> pretty(output('A'))
output A
return ()

Now is the moment of truth. Does this monad generated using Free satisfy monad laws?

scala> pretty(output('A'))
output A
return ()

scala> pretty(pointed('A') >>= output)
output A
return ()

scala> pretty(output('A') >>= pointed)
output A
return ()

scala> pretty((output('A') >> done) >> output('C'))
output A
done

scala> pretty(output('A') >> (done >> output('C')))
output A
done

Looking good. Also notice the “abort” semantics of done.

Free monads part 2 

WFMM:

data Free f r = Free (f (Free f r)) | Pure r
data List a   = Cons  a (List a  )  | Nil

In other words, we can think of a free monad as just being a list of functors. The Free constructor behaves like a Cons, prepending a functor to the list, and the Pure constructor behaves like Nil, representing an empty list (i.e. no functors).

And here’s part 3.

Free monads part 3 

WFMM:

The free monad is the interpreter’s best friend. Free monads “free the interpreter” as much as possible while still maintaining the bare minimum necessary to form a monad.

On the flip side, from the program writer’s point of view, free monads do not give anything but being sequential. The interpreter needs to provide some run function to make it useful. The point, I think, is that given a data structure that satisfies Functor, Free provides minimal monads automatically.

Another way of looking at it is that Free monad provides a way of building a syntax tree given a container.

Stackless Scala with Free Monads 

Now that we have general understanding of Free monads, let’s watch Rúnar’s presentation from Scala Days 2012: Stackless Scala With Free Monads. I recommend watching the talk before reading the paper, but it’s easier to quote the paper version Stackless Scala With Free Monads.

Rúnar starts out with a code that uses State monad to zip a list with index. It blows the stack when the list is larger than the stack limit. Then he introduces tranpoline, which is a single loop that drives the entire program.

sealed trait Trampoline [+ A] {
  final def runT : A =
    this match {
      case More (k) => k().runT
      case Done (v) => v
    }
}
case class More[+A](k: () => Trampoline[A])
  extends Trampoline[A]
case class Done [+A](result: A)
  extends Trampoline [A]

In the above code, Function0 k is used as a thunk for the next step.

To extend its usage for State monad, he then reifies flatMap into a data structure called FlatMap:

case class FlatMap [A,+B](
  sub: Trampoline [A],
  k: A => Trampoline[B]) extends Trampoline[B]

Next, it is revealed that Trampoline is a free monad of Function0. Here’s how it’s defined in Scalaz 7:

  type Trampoline[+A] = Free[Function0, A]

Free monads 

In addition, Rúnar introduces several data structures that can form useful free monad:

type Pair[+A] = (A, A)
type BinTree[+A] = Free[Pair, A]

type Tree[+A] = Free[List, A]

type FreeMonoid[+A] = Free[({type λ[+α] = (A,α)})#λ, Unit]

type Trivial[+A] = Unit
type Option[+A] = Free[Trivial, A]

There’s also iteratees implementation based on free monads. Finally, he summarizes free monads in nice bullet points:

• A model for any recursive data type with data at the leaves.
• A free monad is an expression tree with variables at the leaves and flatMap is variable substitution.

Trampoline 

Using Trampoline any program can be transformed into a stackless one. Let’s try implementing even and odd from the talk using Scalaz 7’s Trampoline. Free object extends FreeFunction which defines a few useful functions for tramplining:

trait FreeFunctions {
  /** Collapse a trampoline to a single step. */
  def reset[A](r: Trampoline[A]): Trampoline[A] = { val a = r.run; return_(a) }

  /** Suspend the given computation in a single step. */
  def return_[S[+_], A](value: => A)(implicit S: Pointed[S]): Free[S, A] =
    Suspend[S, A](S.point(Return[S, A](value)))

  def suspend[S[+_], A](value: => Free[S, A])(implicit S: Pointed[S]): Free[S, A] =
    Suspend[S, A](S.point(value))

  /** A trampoline step that doesn't do anything. */
  def pause: Trampoline[Unit] =
    return_(())

  ...
}

We can call import Free._ to use these.

scala> import Free._
import Free._

scala> :paste
// Entering paste mode (ctrl-D to finish)

def even[A](ns: List[A]): Trampoline[Boolean] =
  ns match {
    case Nil => return_(true)
    case x :: xs => suspend(odd(xs))
  }
def odd[A](ns: List[A]): Trampoline[Boolean] =
  ns match {
    case Nil => return_(false)
    case x :: xs => suspend(even(xs))
  }

// Exiting paste mode, now interpreting.

even: [A](ns: List[A])scalaz.Free.Trampoline[Boolean]
odd: [A](ns: List[A])scalaz.Free.Trampoline[Boolean]

scala> even(List(1, 2, 3)).run
res118: Boolean = false

scala> even(0 |-> 3000).run
res119: Boolean = false

This was surprisingly simple.

List using Free 

Let’s try defining “List” using Free.

scala> type FreeMonoid[A] = Free[({type λ[+α] = (A,α)})#λ, Unit]
defined type alias FreeMonoid

scala> def cons[A](a: A): FreeMonoid[A] = Free.Suspend[({type λ[+α] = (A,α)})#λ, Unit]((a, Free.Return[({type λ[+α] = (A,α)})#λ, Unit](())))
cons: [A](a: A)FreeMonoid[A]

scala> cons(1)
res0: FreeMonoid[Int] = Suspend((1,Return(())))

scala> cons(1) >>= {_ => cons(2)}
res1: scalaz.Free[[+α](Int, α),Unit] = Gosub(Suspend((1,Return(()))),<function1>)

As a way of interpretting the result, let’s try converting this to a standard List:

scala> def toList[A](list: FreeMonoid[A]): List[A] =
         list.resume.fold(
           { case (x: A, xs: FreeMonoid[A]) => x :: toList(xs) },
           { _ => Nil })

scala> toList(res1)
res4: List[Int] = List(1, 2)

That’s it for today.

day 19 

It’s no secret that some of the fundamentals of Scalaz and Haskell like Monoid and Functor comes from category theory. Let’s try studying category theory and see if we can use the knowledge to further our understanding of Scalaz.

Category theory 

The most accessible category theory book I’ve come across is Lawvere and Schanuel’s Conceptual Mathematics: A First Introduction to Categories 2nd ed. The book mixes Articles, which is written like a normal textbook; and Sessions, which is kind of written like a recitation class.

Even in the Article section, CM uses many pages to go over the basic concept compared to other books, which is good for self learners.

Sets, arrows, composition 

CM:

Before giving a precise definition of ‘category’, we should become familiar with one example, the category of finite sets and maps. An object in this category is a finite set or collection. … You are probably familiar with some notations for finite sets:

{ John, Mary, Sam }

There are two ways that I can think of to express this in Scala. One is by using a value a: Set[Person]:

scala> :paste

sealed trait Person {}
case object John extends Person {}
case object Mary extends Person {}
case object Sam extends Person {}

val a: Set[Person] = Set[Person](John, Mary, Sam)

// Exiting paste mode, now interpreting.

Another way of looking at it, is that Person as the type is a finite set already without Set. Note: In CM, Lawvere and Schanuel use the term “map”, but I’m going to change to arrow like Mac Lane and other books.

A arrow f in this cateogry consists of three things:

1. a set A, called the domain of the arrow,
2. a set B, called the codomain of the arrow,
3. a rule assigning to each element a in the domain, an element b in the codomain. This b is denoted by f ∘ a (or sometimes ’f(a)‘), read ’f of a‘.

(Other words for arrow are ‘function’, ‘transformation’, ‘operator’, ‘map’, and ‘morphism’.)

Let’s try implementing the favorite breakfast arrow.

scala> :paste

sealed trait Breakfast {}
case object Eggs extends Breakfast {}
case object Oatmeal extends Breakfast {}
case object Toast extends Breakfast {}
case object Coffee extends Breakfast {}

val favoriteBreakfast: Person => Breakfast = {
  case John => Eggs
  case Mary => Coffee
  case Sam  => Coffee
}

// Exiting paste mode, now interpreting.

favoriteBreakfast: Person => Breakfast = <function1>

Note here that an “object” in this category is Set[Person] or Person, but the “arrow” favoriteBreakfast accepts a value whose type is Person. Here’s the internal diagram of the arrow.

The important thing is: For each dot in the domain, we have exactly one arrow leaving, and the arrow arrives at some dot in the codomain.

I get that a map can be more general than Function1[A, B] but it’s ok for this category. Here’s the implementation of favoritePerson:

scala> val favoritePerson: Person => Person = {
         case John => Mary
         case Mary => John
         case Sam  => Mary
       }
favoritePerson: Person => Person = <function1>

An arrow in which the domain and codomain are the same object is called an endomorphism.

An arrow, in which the domain and codomain are the same set A, and for each of a in A, f(a) = a, is called an identity arrow.

The “identity arrow on A” is denoted as 1_A.

Again, identity is an arrow, so it works on an element in the set, not the set itself. So in this case we can just use scala.Predef.identity.

scala> identity(John)
res0: John.type = John

Here are the external diagrams corresponding to the three internal diagrams from the above.

This reiterates the point that in the category of finite sets, the “objects” translate to types like Person and Breakfast, and arrows translate to functions like Person => Person. The external diagram looks a lot like the type-level signatures like Person => Person.

The final basic ingredient, which is what lends all the dynamics to the notion of category is composition of arrows, by which two arrows are combined to obtain a third arrow.

We can do this in scala using scala.Function1’s andThen or compose.

scala> val favoritePersonsBreakfast = favoriteBreakfast compose favoritePerson
favoritePersonsBreakfast: Person => Breakfast = <function1>

Here’s the internal diagram:

and the external diagram:

After composition the external diagram becomes as follows:

’f ∘ g’ is read ’f following g‘, or sometimes ’f of g‘.

Data for a category consists of the four ingredients:

• objects: A, B, C, …
• arrows: f: A => B
• identity arrows: 1_A: A => A
• composition of arrows

These data must satisfy the following rules:

The identity laws:

• If 1_A: A => A, g: A => B, then g ∘ 1_A = g
• If f: A => B, 1_B: B => B, then 1_A ∘ f = f

The associative law:

• If f: A => B, g: B => C, h: C => D, then h ∘ (g ∘ f) = (h ∘ g) ∘ f

Point 

CM:

One very useful sort of set is a ‘singleton’ set, a set with exactly one element. Fix one of these, say {me}, and call this set ’1‘.

Definition: A point of a set X is an arrows 1 => X. … (If A is some familiar set, an arrow from A to X is called an ’A-element’ of X; thus ’1-elements’ are points.) Since a point is an arrow, we can compose it with another arrow, and get a point again.

If I understand what’s going on, it seems like CM is redefining the concept of the element as a special case of arrow. Another name for singleton is unit set, and in Scala it is (): Unit. So it’s analogous to saying that values are sugar for Unit => X.

scala> val johnPoint: Unit => Person = { case () => John } 
johnPoint: Unit => Person = <function1>

scala> favoriteBreakfast compose johnPoint
res1: Unit => Breakfast = <function1>

scala> res1(())
res2: Breakfast = Eggs

First-class functions in programming languages that support fp treat functions as values, which allows higher-order functions. Category theory unifies on the other direction by treating values as functions.

Session 2 and 3 contain nice review of Article I, so you should read them if you own the book.

Equality of arrows of sets 

One part in the sessions that I thought was interesting was about the equality of arrows. Many of the discussions in category theory involves around equality of arrows, but how we test if an arrow f is equal to g?

Two maps are equal when they have the same three ingredients:

• domain A
• codomain B
• a rule that assigns f ∘ a

Because of 1, we can test for equality of arrows of sets f: A => B and g: A => B using this test:

If for each point a: 1 => A, f ∘ a = g ∘ a, then f = g.

This reminds me of scalacheck. Let’s try implementing a check for f: Person => Breakfast:

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait Person {}
case object John extends Person {}
case object Mary extends Person {}
case object Sam extends Person {}

sealed trait Breakfast {}
case object Eggs extends Breakfast {}
case object Oatmeal extends Breakfast {}
case object Toast extends Breakfast {}
case object Coffee extends Breakfast {}

val favoriteBreakfast: Person => Breakfast = {
  case John => Eggs
  case Mary => Coffee
  case Sam  => Coffee
}

val favoritePerson: Person => Person = {
  case John => Mary
  case Mary => John
  case Sam  => Mary
}

val favoritePersonsBreakfast = favoriteBreakfast compose favoritePerson

// Exiting paste mode, now interpreting.

scala> import org.scalacheck.{Prop, Arbitrary, Gen}
import org.scalacheck.{Prop, Arbitrary, Gen}

scala> def arrowEqualsProp(f: Person => Breakfast, g: Person => Breakfast)
         (implicit ev1: Equal[Breakfast], ev2: Arbitrary[Person]): Prop =
         Prop.forAll { a: Person =>
           f(a) === g(a)
         } 
arrowEqualsProp: (f: Person => Breakfast, g: Person => Breakfast)
(implicit ev1: scalaz.Equal[Breakfast], implicit ev2: org.scalacheck.Arbitrary[Person])org.scalacheck.Prop

scala> implicit val arbPerson: Arbitrary[Person] = Arbitrary {
         Gen.oneOf(John, Mary, Sam)
       }
arbPerson: org.scalacheck.Arbitrary[Person] = org.scalacheck.Arbitrary$$anon$2@41ec9951

scala> implicit val breakfastEqual: Equal[Breakfast] = Equal.equalA[Breakfast]
breakfastEqual: scalaz.Equal[Breakfast] = scalaz.Equal$$anon$4@783babde

scala> arrowEqualsProp(favoriteBreakfast, favoritePersonsBreakfast)
res0: org.scalacheck.Prop = Prop

scala> res0.check
! Falsified after 1 passed tests.
> ARG_0: John

scala> arrowEqualsProp(favoriteBreakfast, favoriteBreakfast)
res2: org.scalacheck.Prop = Prop

scala> res2.check
+ OK, passed 100 tests.

We can generalize arrowEqualsProp a bit:

scala> def arrowEqualsProp[A, B](f: A => B, g: A => B)
         (implicit ev1: Equal[B], ev2: Arbitrary[A]): Prop =
         Prop.forAll { a: A =>
           f(a) === g(a)
         } 
arrowEqualsProp: [A, B](f: A => B, g: A => B)
(implicit ev1: scalaz.Equal[B], implicit ev2: org.scalacheck.Arbitrary[A])org.scalacheck.Prop

scala> arrowEqualsProp(favoriteBreakfast, favoriteBreakfast)
res4: org.scalacheck.Prop = Prop

scala> res4.check
+ OK, passed 100 tests.

Isomorphisms 

CM:

Definitions: An arrow f: A => B is called an isomorphism, or invertible arrow, if there is a map g: B => A, for which g ∘ f = 1_A and f ∘ g = 1_B. An arrow g related to f by satisfying these equations is called an inverse for f. Two objects A and B are said to be isomorphic if there is at least one isomorphism f: A => B.

In Scalaz you can express this using the traits defined in Isomorphism.

sealed abstract class Isomorphisms extends IsomorphismsLow0{
  /**Isomorphism for arrows of kind * -> * -> * */
  trait Iso[Arr[_, _], A, B] {
    self =>
    def to: Arr[A, B]
    def from: Arr[B, A]
  }

  /**Set isomorphism */
  type IsoSet[A, B] = Iso[Function1, A, B]

  /**Alias for IsoSet */
  type <=>[A, B] = IsoSet[A, B]
}

object Isomorphism extends Isomorphisms

It also contains isomorphism for higher kinds, but IsoSet would do for now.

scala> :paste
// Entering paste mode (ctrl-D to finish)

sealed trait Family {}
case object Mother extends Family {}
case object Father extends Family {}
case object Child extends Family {}

sealed trait Relic {}
case object Feather extends Relic {}
case object Stone extends Relic {}
case object Flower extends Relic {}

import Isomorphism.<=>
val isoFamilyRelic = new (Family <=> Relic) {
  val to: Family => Relic = {
    case Mother => Feather
    case Father => Stone
    case Child  => Flower
  }
  val from: Relic => Family = {
    case Feather => Mother
    case Stone   => Father
    case Flower  => Child
  }
}

isoFamilyRelic: scalaz.Isomorphism.<=>[Family,Relic]{val to: Family => Relic; val from: Relic => Family} = 1@12e3914c

It’s encouraging to see support for isomorphisms in Scalaz. Hopefully we are going the right direction.

Notation: If f: A => B has an inverse, then the (one and only) inverse for f is denoted by the symbol f^-1 (read ’f-inverse’ or ‘the inverse of f‘.)

We can check if the above isoFamilyRelic satisfies the definition using arrowEqualsProp.

scala> :paste
// Entering paste mode (ctrl-D to finish)

implicit val familyEqual = Equal.equalA[Family]
implicit val relicEqual = Equal.equalA[Relic]
implicit val arbFamily: Arbitrary[Family] = Arbitrary {
  Gen.oneOf(Mother, Father, Child)
}
implicit val arbRelic: Arbitrary[Relic] = Arbitrary {
  Gen.oneOf(Feather, Stone, Flower)
}

// Exiting paste mode, now interpreting.

scala> arrowEqualsProp(isoFamilyRelic.from compose isoFamilyRelic.to, identity[Family] _)
res22: org.scalacheck.Prop = Prop

scala> res22.check
+ OK, passed 100 tests.

scala> arrowEqualsProp(isoFamilyRelic.to compose isoFamilyRelic.from, identity[Relic] _)
res24: org.scalacheck.Prop = Prop

scala> res24.check
+ OK, passed 100 tests.

Determination and choice 

CM:

1. The ‘determination’ (or ‘extension’) problem
Given f and h as shown, what are all g, if any, for which h = g ∘ f?

2. The ‘choice’ (or ‘lifting’) problem
Given g and h as shown, what are all g, if any, for which h = g ∘ f?

These two notions are analogous to division problem.

Retractions and sections 

Definitions: If f: A => B:

• a retraction for f is an arrow r: B => A for which r ∘ f = 1_A
• a section for f is an arrow s: B => A for which f ∘ s = 1_B

Here’s the external diagram for retraction problem:

and one for section problem:

Surjective 

If an arrow f: A => B satisfies the property ‘for any y: T => B there exists an x: T => A such that f ∘ x = y‘, it is often said to be ‘surjective for arrows from T.’

I came up with my own example to think about what surjective means in set theory:

Suppose John and friends are on their way to India, and they are given two choices for their lunch in the flight: chicken wrap or spicy chick peas. Surjective means that given a meal, you can find at least one person who chose the meal. In other words, all elements in codomain are covered.

Now recall that we can generalize the concept of elements by introducing singleton explicitly.

Compare this to the category theory’s definition of surjective: for any y: T => B there exists an x: T => A such that f ∘ x = y. For any arrow going from 1 to B (lunch), there is an arrow going from 1 to A (person) such that f ∘ x = y. In other words, f is surjective for arrows from 1.

Let’s look at this using an external diagram.

This is essentially the same diagram as the choice problem.

Injective and monomorphism 

Definitions: An arrow f satisfying the property ‘for any pair of arrows x₁: T => A and x₂: T => A, if f ∘ x₁ = f ∘ x₂ then x₁ = x₂‘, it is said to be injective for arrows from T.

If f is injective for arrows from T for every T, one says that f is injective, or is a monomorphism.

Here’s how injective would mean in terms of sets:

All elements in codomain are mapped only once. We can imagine a third object T, which maps to John, Mary, and Sam. Any of the composition would still land on a unique meal. Here’s the external diagram: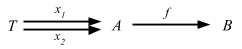

Epimorphism 

Definition: An arrow f with this cancellation property ‘if t₁ ∘ f = t₂ ∘ f then t₁ = t₂’ for every T is called an epimorphism.

Apparently, this is a generalized form of surjective, but the book doesn’t go into detail, so I’ll skip over.

Idempotent 

Definition: An endomorphism e is called idempotent if e ∘ e = e.

Automorphism 

An arrow, which is both an endomorphism and at the same time an isomorphism, usually called by one word automorphism.

I think we’ve covered enough ground. Breaking categories apart into internal diagrams really helps getting the hang of it.

day 20 

On day 19 we started looking at basic concepts in category theory using Lawvere and Schanuel’s Conceptual Mathematics: A First Introduction to Categories. The book is a good introduction book into the notion of category since it spends a lot of pages explaining the basic concepts using concrete examples. The very aspect gets a bit annoying when you want to move on to more advanced concept, since it’s goes winding around.

Awodey’s ‘Category Theory‘ 

Today I’m switching to Steve Awodey’s Category Theory. This is also a book written for non-mathematicians, but goes at faster pace, and more emphasis is placed on thinking in abstract terms.

A particular definition or a theorem is called abstract, when it relies only on category theoric notions, rather than some additional information about the objects and arrows. The advantage of an abstract notion is that it applies in any category immediately.

Definition 1.3 In any category C, an arrow f: A => B is called an isomorphism, if there is an arrow g: B => A in C such that:

g ∘ f = 1_A and f ∘ g = 1_B.

Awodey names the above definition to be an abstract notion as it does make use only of category theoric notion.

Extending this to Scalaz, learning the nature of an abtract typeclass has the advantage of it applying in all concrete data structures that support it.

Examples of categories 

Before we go abtract, we’re going to look at some more concrete categories. This is actually a good thing, since we only saw one category yesterday.

Sets 

The category of sets and total functions are denoted by Sets written in bold.

Sets_fin 

The category of all finite sets and total functions between them are called Sets_fin. This is the category we have been looking at so far.

Pos 

Awodey:

Another kind of example one often sees in mathematics is categories of structured sets, that is, sets with some further “structure” and functions that “preserve it,” where these notions are determined in some independent way.

A partially ordered set or poset is a set A equipped with a binary relation a ≤_A b such that the following conditions hold for all a, b, c ∈ A:

• reflexivity: a ≤_A a
• transitivity: if a ≤_A b and b ≤_A c, then a ≤_A c
• antisymmetry: if a ≤_A b and b ≤_A a, then a = b

An arrow from a poset A to a poset B is a function m: A => B that is monotone, in the sense that, for all a, a’ ∈ A,

• a ≤_A a’ implies m(a) ≤_A m(a’).

As long as the functions are monotone, the objects will continue to be in the category, so the “structure” is preserved. The category of posets and monotone functions is denoted as Pos. Awodey likes posets, so it’s important we understand it.

Cat 

Definition 1.2. A functor
F: C => D
between categories C and D is a mapping of objects to objects and arrows to arrows, in such a way that.

• F(f: A => B) = F(f): F(A) => F(B)
• F(1_A) = 1_F(A)
• F(g ∘ f) = F(g) ∘ F(f)

That is, F, preserves domains and codomains, identity arrows, and composition.

Now we are talking. Functor is an arrow between two categories. Here’s the external diagram:

The fact that the positions of F(A), F(B), and F(C) are distorted is intentional. That’s what F is doing, slightly distorting the picture, but still preserving the composition.

This category of categories and functors is denoted as Cat.

Monoid 

A monoid (sometimes called a semigroup with unit) is a set M equipped with a binary operation ·: M × M => M and a distinguished “unit” element u ∈ M such that for all x, y, z ∈ M,

• x · (y · z) = (x · y) · z
• u · x = x = x · u

Equivalently, a monoid is a category with just one object. The arrows of the category are the elements of the monoid. In particular, the identity arrow is the unit element u. Composition of arrows is the binary operation m · n for the monoid.

The concept of monoid translates well into Scalaz. You can check out About those Monoids from day 3.

trait Monoid[A] extends Semigroup[A] { self =>
  ////
  /** The identity element for `append`. */
  def zero: A
  
  ...
}

trait Semigroup[A]  { self =>
  def append(a1: A, a2: => A): A
  ...
}

Here is addition of Int and 0:

scala> 10 |+| Monoid[Int].zero
res26: Int = 10

and multiplication of Int and 1:

scala>  Tags.Multiplication(10) |+| Monoid[Int @@ Tags.Multiplication].zero
res27: scalaz.@@[Int,scalaz.Tags.Multiplication] = 10

The idea that these monoids are categories with one object and that elements are arrows used to sound so alien to me, but now it’s understandable since we were exposed to singleton.

Mon 

The category of monoids and functions that preserve the monoid structure is denoted by Mon. These arrows that preserve structure are called homomorphism.

In detail, a homomorphism from a monoid M to a monoid N is a function h: M => N such that for all m, n ∈ M,

• h(m ·_M n) = h(m) ·_N h(n)
• h(u_M) = u_N

Since a monoid is a category, a monoid homomorphism is a special case of functors.

Groups 

Definition 1.4 A group G is a monoid with an inverse g^-1 for every element g. Thus, G is a category with one object, in which every arrow is an isomorphism.

The category of groups and group homomorphisms is denoted as Groups.

Scalaz used to have groups, but it was removed about an year ago in #279, which says it’s removing duplication with Spire.

Initial and terminal objects 

Let’s look at something abstract. When a definition relies only on category theoretical notion (objects and arrows), it often reduces down to a form “given a diagram abc, there exists a unique x that makes another diagram xyz commute.” Commutative in this case mean that all the arrows compose correctly.Those defenitions are called universal property or universal mapping property (UMP).

Some of the notions have a counterpart in set theory, but it’s more powerful because of its abtract nature. Consider making the empty set and the one-element sets in Sets abstract.

Definition 2.9. In any category C, an object

• 0 is initial if for any object C there is a unique morphism
  0 => C
• 1 is terminal if for any object C there is a unique morphism
  C => 1

Uniquely determined up to isomorphism 

As a general rule, the uniqueness requirements of universal mapping properties are required only up to isomorphisms. Another way of looking at it is that if objects A and B are isomorphic to each other, they are “equal in some sense.” To signify this, we write A ≅ B.

Proposition 2.10 Initial (terminal) objects are unique up to isomorphism.
Proof. In fact, if C and C’ are both initial (terminal) in the same category, then there’s a unique isomorphism C => C’. Indeed, suppose that 0 and 0’ are both initial objects in some category C; the following diagram then makes it clear that 0 and 0’ are uniquely isomorphic:

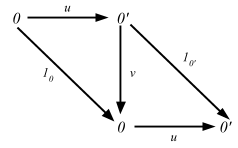
Given that isomorphism is defined by g ∘ f = 1_A and f ∘ g = 1_B, this looks good.

Examples 

In Sets, the empty set is initial and any singleton set {x} is terminal.

So apparently there’s a concept called an empty function that maps from an empty set to any set.

In a poset, an object is plainly initial iff it is the least element, and terminal iff it is the greatest element.

This kind of makes sense, since in a poset we need to preserve the structure using ≤.

There are many other examples, but the interesting part is that seemingly unrelated concepts share the same structure.

Products 

Let us begin by considering products of sets. Given sets A and B, the cartesian product of A and B is the set of ordered pairs
A × B = {(a, b)| a ∈ A, b ∈ B}

There are two coordinate projections:

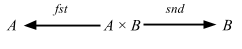
with:

• fst ∘ (a, b) = a
• snd ∘ (a, b) = b

This notion of product relates to scala.Product, which is the base trait for all tuples and case classes.

For any element in c ∈ A × B, we have c = (fst ∘ c, snd ∘ c)

Using the same trick as yesterday, we can introduce the singleton explicitly:

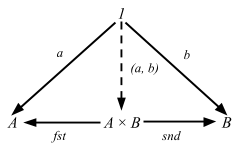
The (external) diagram captures what we stated in the above. If we replace 1-elements by generalized elements, we get the categorical definition.

Definition 2.15. In any category C, a product diagram for the objects A and B consists of an object P and arrows p₁ and p₂

satisfying the following UMP:

Given any diagram of the form

there exists a unique u: X => P, making the diagram

commute, that is, such that x₁ = p₁ u and x₂ = p₂ u.

Because this is universal, this applies to any category.

Uniqueness of products 

UMP also suggests that all products of A and B are unique up to isomorphism.

Proposition 2.17 Products are unique up to isomorphism.

Suppose we have P and Q that are products of objects A and B.

1. Because P is a product, there is a unique i: P => Q such that p₁ = q₁ ∘ i and p₂ = q₂ ∘ i
2. Because Q is a product, there is a unique j: Q => P such that q₁ = p₁ ∘ j and q₂ = p₂ ∘ j
3. By composing j and i we get 1_P = j ∘ i
4. Similarly, we can also get 1_Q = i ∘ j
5. Thus i is an isomorphism, and P ≅ Q ∎

Since all products are isometric, we can just denote one as A × B, and the arrow u: X => A × B is denoted as ⟨x₁, x₂⟩.

Examples 

We saw that in Sets, cartesian product is a product.

Let P be a poset and consider a product of elements p, q ∈ P. We must have projections

• p × q ≤ p
• p × q ≤ q

and if for any element x, x ≤ p, and x ≤ q
then we need

• x ≤ p × q

In this case, p × q becomes greatest lower bound.

Duality 

Opposite category 

Before we get into duality, we need to cover the concept of generating a category out of an existing one. Note that we are no longer talking about objects, but a category, which includes objects and arrows.

The opposite (or “dual”) category C^op of a category C has the same objects as C, and an arrow f: C => D in C^op is an arrow f: D => C in C. That is, C^op is just C with all of the arrows formally turned around.

The duality principle 

If we take the concept further, we can come up with “dual statement” Σ^* by substituting any sentence Σ in the category theory by replacing the following:

• f ∘ g for g ∘ f
• codomain for domain
• domain for codomain

Since there’s nothing semantically important about which side is f or g, the dual statement also holds true as long as Σ only relies on category theory. In other words, any proof that holds for one concept also holds for its dual. This is called the duality principle.

Another way of looking at it is that if Σ holds in all C, it should also hold in C^op, and so Σ^* should hold in (C^op)^op, which is C.

Let’s look at the definitions of initial and terminal again:

Definition 2.9. In any category C, an object

• 0 is initial if for any object C there is a unique morphism
  0 => C
• 1 is terminal if for any object C there is a unique morphism
  C => 1

They are dual to each other, so the initials in C are terminals in C^op.

Recall proof for “the initial objects are unique up to isomorphism.”

If you flip the direction of all arrows in the above diagram, you do get a proof for terminals.

This is pretty cool. Let’s continue from here later.

day 21 

On day 20 we continued to look into concepts from category theory, but using Awodey as the guide with more enphasis on thinking in abstract terms. In particuar, I was aiming towards the notion of duality, which says that an abtract concept in category theory should hold when you flip the direction of all the arrows.

Coproducts 

One of the well known dual concepts is coproduct, which is the dual of product. Prefixing with “co-” is the convention to name duals.

Here’s the definition of products again:

Definition 2.15. In any category C, a product diagram for the objects A and B consists of an object P and arrows p₁ and p₂

satisfying the following UMP:

Given any diagram of the form

there exists a unique u: X => P, making the diagram

commute, that is, such that x₁ = p₁ u and x₂ = p₂ u.

Flip the arrows around, and we get a coproduct diagram:

Since coproducts are unique up to isomorphism, we can denote the coproduct as A + B, and [f, g] for the arrow u: A + B => X.

The “coprojections” i₁: A => A + B and i₂: B => A + B are usually called injections, even though they need not be “injective” in any sense.

Similar to the way products related to product type encoded as scala.Product, coproducts relate to the notion of sum type, or union type, like this:

data TrafficLight = Red | Yellow | Green

Unboxed union types 

Using case class and sealed traits as encoding for this doesn’t work well in some cases like if I wanted a union of Int and String. An interesting read on this topic is Miles Sabin (@milessabin)’s Unboxed union types in Scala via the Curry-Howard isomorphism.

Everyone’s seen De Morgan’s law:
!(A || B) <=> (!A && !B)
Since Scala has conjunction via A with B, Miles discovered that we can get disjunction if we can encode negation. This is ported to Scalaz under scalaz.UnionTypes:

trait UnionTypes {
  type ![A] = A => Nothing
  type !![A] = ![![A]]

  trait Disj { self =>
    type D
    type t[S] = Disj {
      type D = self.D with ![S]
    }
  }

  type t[T] = {
    type t[S] = (Disj { type D = ![T] })#t[S]
  }

  type or[T <: Disj] = ![T#D]

  type Contains[S, T <: Disj] = !![S] <:< or[T]
  type ∈[S, T <: Disj] = Contains[S, T]

  sealed trait Union[T] {
    val value: Any
  }
}

object UnionTypes extends UnionTypes

Let’s try implementing Miles’s size example:

scala> import UnionTypes._
import UnionTypes._

scala> type StringOrInt = t[String]#t[Int]
defined type alias StringOrInt

scala> implicitly[Int ∈ StringOrInt]
res0: scalaz.UnionTypes.∈[Int,StringOrInt] = <function1>

scala> implicitly[Byte ∈ StringOrInt]
<console>:18: error: Cannot prove that Byte <:< StringOrInt.
              implicitly[Byte ∈ StringOrInt]
                        ^

scala> def size[A](a: A)(implicit ev: A ∈ StringOrInt): Int = a match {
         case i: Int    => i
         case s: String => s.length  
       }
size: [A](a: A)(implicit ev: scalaz.UnionTypes.∈[A,StringOrInt])Int

scala> size(23)
res2: Int = 23

scala> size("foo")
res3: Int = 3

\/ 

Scalaz also has \/, which could be thought of as a form of sum type. The symbolic name \/ kind of makes sense since ∨ means the logical disjunction. This was covered in day 7: \/. We can rewrite the size example as follows:

scala> def size(a: String \/ Int): Int = a match {
         case \/-(i) => i
         case -\/(s) => s.length  
       }
size: (a: scalaz.\/[String,Int])Int

scala> size(23.right[String])
res15: Int = 23

scala> size("foo".left[Int])
res16: Int = 3

Coproduct and Inject 

There is actually Coproduct in Scalaz, which is like an Either on type constructor:

final case class Coproduct[F[_], G[_], A](run: F[A] \/ G[A]) {
  ...
}

object Coproduct extends CoproductInstances with CoproductFunctions

trait CoproductFunctions {
  def leftc[F[_], G[_], A](x: F[A]): Coproduct[F, G, A] =
    Coproduct(-\/(x))

  def rightc[F[_], G[_], A](x: G[A]): Coproduct[F, G, A] =
    Coproduct(\/-(x))

  ...
}

In Data types à la carte Wouter Swierstra (@wouterswierstra) describes how this could be used to solve the so-called Expression Problem:

The goal is to define a data type by cases, where one can add new cases to the data type and new functions over the data type, without recompiling existing code, and while retaining static type safety.

The automatic injections described in this paper was contributed to Scalaz in #502 by @ethul. An example of how this could be used is available in his typeclass-inject’s README.

Individual expressions construct Free[F, Int] where F is the coproduct of all three algebras.

Hom-sets 

We need to pick up some of the fundamentals that I skipped over.

Large, small, and locally small 

Definition 1.11. A category C is called small if both the collection C₀ of objects of C and the collection C₁ of arrows of C are sets. Otherwise, C is called large.

For example, all finite categories are clearly small, as is the category Sets_fin of finite sets and functions.

Cat is actually a category of all small categories, so Cat doesn’t contain itself.

Definition 1.12. A category C is called locally small if for all objects X, Y in C, the collection Hom_C(X, Y) = { f ∈ C₁ | f: X = Y } is a set (called a hom-set)

Hom-sets 

A Hom-set Hom(A, B) is a set of arrows between objects A and B. Hom-sets are useful because we can use it to inspect (look into the elements) an object using just arrows.

Putting any arrow f: A => B in C into Hom(X, A) would create a function:

• Hom(X, f): Hom(X, A) => Hom(X, B)
• case x => (f ∘ x: X => A => B)

Thus, Hom(X, f) = f ∘ _.

By using the singleton trick in Sets, we can exploit A ≅ Hom_Sets(1, A). If we generalize this we can think of Hom(X, A) as a set of generalized elements from X.

We can then create a functor out of this by replacing A with _
Hom(X, _): C => Sets.

This functor is called the representable functor, or covariant hom-functor.

Thinking in Hom-set 

For any object P, a pair of arrows p₁: P => A and p₂: P => B determine an element (p₁, p₂) of the set
Hom(P, A) × Hom(P, B).

We see that given x: X => P we can derive x₁ and x₂ by composing with p₁ and p₂ respectively. Because compositions are functions in Hom sets, we could express the above as a function too:

ϑ_X = (Hom(X, p₁), Hom(X, p₂)): Hom(X, P) => Hom(X, A) × Hom(X, B)
where ϑ_X(x) = (x₁, x₂)

That’s a cursive theta, by the way.

Proposition 2.20. A diagram of the form

is a product for A and B iff for every object X, the canonical function ϑ_X given in (2.1) is an isomorphism,
ϑ_X: Hom(X, P) ≅ Hom(P, A) × Hom(P, B).

This is pretty interesting because we just replaced a diagram with an isomorphic equation.

Natural Transformation 

I think we now have enough ammunition on our hands to tackle naturality. Let’s skip to the middle of the book, section 7.4.

A natural transformation is a morphism of functors. That is right: for fix categories C and D, we can regard the functors C => D as the object of a new category, and the arrows between these objects are what we are going to call natural transformations.

There are some interesting blog posts around natural transformation in Scala:

• Higher-Rank Polymorphism in Scala, Rúnar (@runarorama) July 2, 2010
• Type-Level Programming in Scala, Part 7: Natural transformation literals, Mark Harrah (@harrah) October 26, 2010
• First-class polymorphic function values in shapeless (2 of 3) — Natural Transformations in Scala, Miles Sabin (@milessabin) May 10, 2012

Mark presents a simple example of why we might want a natural transformation:

We run into problems when we proceed to natural transformations. We are not able to define a function that maps an Option[T] to List[T] for every T, for example. If this is not obvious, try to define toList so that the following compiles:

val toList = ...

val a: List[Int] = toList(Some(3))
assert(List(3) == a)

val b: List[Boolean] = toList(Some(true))
assert(List(true) == b)

In order to define a natural transformation M ~> N (here, M=Option, N=List), we have to create an anonymous class because Scala doesn’t have literals for quantified functions.

Scalaz ports this. Let’s see NaturalTransformation:

/** A universally quantified function, usually written as `F ~> G`,
  * for symmetry with `A => B`.
  * ....
  */
trait NaturalTransformation[-F[_], +G[_]] {
  self =>
  def apply[A](fa: F[A]): G[A]

  ....
}

The aliases are available in the package object for scalaz namespace:

  /** A [[scalaz.NaturalTransformation]][F, G]. */
  type ~>[-F[_], +G[_]] = NaturalTransformation[F, G]
  /** A [[scalaz.NaturalTransformation]][G, F]. */
  type <~[+F[_], -G[_]] = NaturalTransformation[G, F]

Let’s try defining toList:

scala> val toList = new (Option ~> List) {
         def apply[T](opt: Option[T]): List[T] =
           opt.toList
       }
toList: scalaz.~>[Option,List] = 1@2fdb237

scala> toList(3.some)
res17: List[Int] = List(3)

scala> toList(true.some)
res18: List[Boolean] = List(true)

If we compare the terms with category theory, in Scalaz the type constructors like List and Option support Functors which maps between two categories.

trait Functor[F[_]] extends InvariantFunctor[F] { self =>
  ////

  /** Lift `f` into `F` and apply to `F[A]`. */
  def map[A, B](fa: F[A])(f: A => B): F[B]
  ...
}

This is a much contrained representation of a functor compared to more general C => D, but it’s a functor if we think of the type constructors as categories.

Since NaturalTransformation (~>) works at type constructor (first-order kinded type) level, it is an arrow between the functors (or a family of arrows between the categories).

We’ll continue from here later.

Thanks for reading 

This page is a placeholder for the end, but I’ll be updating this series every now and then. Thanks for the comments and retweets!

Kudos to Miran Lipovača for writing Learn You a Haskell for Great Good!. It really helped to have the book as a guide with many examples.

And of course, the authors and contributors of Scalaz deserve some shoutout! Here are the top 10 from the list:

• @retronym Jason Zaugg
• @xuwei-k Kenji Yoshida
• @tonymorris Tony Morris
• @larsrh Lars Hupel
• @runarorama Rúnar
• @S11001001 Stephen Compall
• @purefn Richard Wallace
• @nuttycom Kris Nuttycombe
• @ekmett Edward Kmett
• @pchiusano Paul Chiusano

It was fun learning functional programming through Scalaz, and I hope the learning continues. Oh yea, don’t forget the Scalaz cheat sheet too.

Scalaz cheatsheet 

Equal[A] 

def equal(a1: A, a2: A): Boolean
(1 === 2) assert_=== false
(2 =/= 1) assert_=== true

Order[A] 

def order(x: A, y: A): Ordering
1.0 ?|? 2.0 assert_=== Ordering.LT
1.0 lt 2.0 assert_=== true
1.0 gt 2.0 assert_=== false
1.0 lte 2.0 assert_=== true
1.0 gte 2.0 assert_=== false
1.0 max 2.0 assert_=== 2.0
1.0 min 2.0 assert_=== 1.0

Show[A] 

def show(f: A): Cord
1.0.show assert_=== Cord("1.0")
1.0.shows assert_=== "1.0"
1.0.print assert_=== ()
1.0.println assert_=== ()

Enum[A] extends Order[A] 

def pred(a: A): A
def succ(a: A): A
1.0 |-> 2.0 assert_=== List(1.0, 2.0)
1.0 |--> (2, 5) assert_=== List(1.0, 3.0, 5.0)
// |=>/|==>/from/fromStep return EphemeralStream[A]
(1.0 |=> 2.0).toList assert_=== List(1.0, 2.0)
(1.0 |==> (2, 5)).toList assert_=== List(1.0, 3.0, 5.0)
(1.0.from take 2).toList assert_=== List(1.0, 2.0)
((1.0 fromStep 2) take 2).toList assert_=== List(1.0, 3.0)
1.0.pred assert_=== 0.0
1.0.predx assert_=== Some(0.0)
1.0.succ assert_=== 2.0
1.0.succx assert_=== Some(2.0)
1.0 -+- 1 assert_=== 2.0
1.0 --- 1 assert_=== 0.0
Enum[Int].min assert_=== Some(-2147483648)
Enum[Int].max assert_=== Some(2147483647)

Semigroup[A] 

def append(a1: A, a2: => A): A
List(1, 2) |+| List(3) assert_=== List(1, 2, 3)
List(1, 2) mappend List(3) assert_=== List(1, 2, 3)
1 |+| 2 assert_=== 3
(Tags.Multiplication(2) |+| Tags.Multiplication(3): Int) assert_=== 6
// Tags.Disjunction (||), Tags.Conjunction (&&)
(Tags.Disjunction(true) |+| Tags.Disjunction(false): Boolean) assert_=== true
(Tags.Conjunction(true) |+| Tags.Conjunction(false): Boolean) assert_=== false
(Ordering.LT: Ordering) |+| (Ordering.GT: Ordering) assert_=== Ordering.LT
(none: Option[String]) |+| "andy".some assert_=== "andy".some
(Tags.First('a'.some) |+| Tags.First('b'.some): Option[Char]) assert_=== 'a'.some
(Tags.Last('a'.some) |+| Tags.Last(none: Option[Char]): Option[Char]) assert_=== 'a'.some

Monoid[A] extends Semigroup[A] 

def zero: A
mzero[List[Int]] assert_=== Nil

Functor[F[_]] 

def map[A, B](fa: F[A])(f: A => B): F[B]
List(1, 2, 3) map {_ + 1} assert_=== List(2, 3, 4)
List(1, 2, 3) ∘ {_ + 1} assert_=== List(2, 3, 4)
List(1, 2, 3) >| "x" assert_=== List("x", "x", "x")
List(1, 2, 3) as "x" assert_=== List("x", "x", "x")
List(1, 2, 3).fpair assert_=== List((1,1), (2,2), (3,3))
List(1, 2, 3).strengthL("x") assert_=== List(("x",1), ("x",2), ("x",3))
List(1, 2, 3).strengthR("x") assert_=== List((1,"x"), (2,"x"), (3,"x"))
List(1, 2, 3).void assert_=== List((), (), ())
Functor[List].lift {(_: Int) * 2} (List(1, 2, 3)) assert_=== List(2, 4, 6)

Apply[F[_]] extends Functor[F] 

def ap[A,B](fa: => F[A])(f: => F[A => B]): F[B]
1.some <*> {(_: Int) + 2}.some assert_=== Some(3) // except in 7.0.0-M3
1.some <*> { 2.some <*> {(_: Int) + (_: Int)}.curried.some } assert_=== 3.some
1.some <* 2.some assert_=== 1.some
1.some *> 2.some assert_=== 2.some
Apply[Option].ap(9.some) {{(_: Int) + 3}.some} assert_=== 12.some
Apply[List].lift2 {(_: Int) * (_: Int)} (List(1, 2), List(3, 4)) assert_=== List(3, 4, 6, 8)
(3.some |@| 5.some) {_ + _} assert_=== 8.some
// ^(3.some, 5.some) {_ + _} assert_=== 8.some

Applicative[F[_]] extends Apply[F] 

def point[A](a: => A): F[A]
1.point[List] assert_=== List(1)
1.η[List] assert_=== List(1)

Product/Composition 

(Applicative[Option] product Applicative[List]).point(0) assert_=== (0.some, List(0))
(Applicative[Option] compose Applicative[List]).point(0) assert_=== List(0).some

Bind[F[_]] extends Apply[F] 

def bind[A, B](fa: F[A])(f: A => F[B]): F[B]
3.some flatMap { x => (x + 1).some } assert_=== 4.some
(3.some >>= { x => (x + 1).some }) assert_=== 4.some 
3.some >> 4.some assert_=== 4.some
List(List(1, 2), List(3, 4)).join assert_=== List(1, 2, 3, 4)

Monad[F[_]] extends Applicative[F] with Bind[F] 

// no contract function
// failed pattern matching produces None
(for {(x :: xs) <- "".toList.some} yield x) assert_=== none
(for { n <- List(1, 2); ch <- List('a', 'b') } yield (n, ch)) assert_=== List((1, 'a'), (1, 'b'), (2, 'a'), (2, 'b'))
(for { a <- (_: Int) * 2; b <- (_: Int) + 10 } yield a + b)(3) assert_=== 19
List(1, 2) filterM { x => List(true, false) } assert_=== List(List(1, 2), List(1), List(2), List())

Plus[F[_]] 

def plus[A](a: F[A], b: => F[A]): F[A]
List(1, 2) <+> List(3, 4) assert_=== List(1, 2, 3, 4)

PlusEmpty[F[_]] extends Plus[F] 

def empty[A]: F[A]
(PlusEmpty[List].empty: List[Int]) assert_=== Nil

ApplicativePlus[F[_]] extends Applicative[F] with PlusEmpty[F] 

// no contract function

MonadPlus[F[_]] extends Monad[F] with ApplicativePlus[F] 

// no contract function
List(1, 2, 3) filter {_ > 2} assert_=== List(3)

Foldable[F[_]] 

def foldMap[A,B](fa: F[A])(f: A => B)(implicit F: Monoid[B]): B
def foldRight[A, B](fa: F[A], z: => B)(f: (A, => B) => B): B
List(1, 2, 3).foldRight (0) {_ + _} assert_=== 6
List(1, 2, 3).foldLeft (0) {_ + _} assert_=== 6
(List(1, 2, 3) foldMap {Tags.Multiplication}: Int) assert_=== 6
List(1, 2, 3).foldLeftM(0) { (acc, x) => (acc + x).some } assert_=== 6.some

Traverse[F[_]] extends Functor[F] with Foldable[F] 

def traverseImpl[G[_]:Applicative,A,B](fa: F[A])(f: A => G[B]): G[F[B]]
List(1, 2, 3) traverse { x => (x > 0) option (x + 1) } assert_=== List(2, 3, 4).some
List(1, 2, 3) traverseU {_ + 1} assert_=== 9
List(1.some, 2.some).sequence assert_=== List(1, 2).some
1.success[String].leaf.sequenceU map {_.drawTree} assert_=== "1\n".success[String]

Length[F[_]] 

def length[A](fa: F[A]): Int
List(1, 2, 3).length assert_=== 3

Index[F[_]] 

def index[A](fa: F[A], i: Int): Option[A]
List(1, 2, 3) index 2 assert_=== 3.some
List(1, 2, 3) index 3 assert_=== none

ArrId[=>:[, ]] 

def id[A]: A =>: A

Compose[=>:[, ]] 

def compose[A, B, C](f: B =>: C, g: A =>: B): (A =>: C)
val f1 = (_:Int) + 1
val f2 = (_:Int) * 100
(f1 >>> f2)(2) assert_=== 300
(f1 <<< f2)(2) assert_=== 201

Category[=>:[, ]] extends ArrId[=>:] with Compose[=>:] 

// no contract function

Arrow[=>:[, ]] extends Category[=>:] 

def arr[A, B](f: A => B): A =>: B
def first[A, B, C](f: (A =>: B)): ((A, C) =>: (B, C))
val f1 = (_:Int) + 1
val f2 = (_:Int) * 100
(f1 *** f2)(1, 2) assert_=== (2, 200)
(f1 &&& f2)(1) assert_=== (2,100)

Unapply[TC[_[_]], MA] 

type M[_]
type A
def TC: TC[M]
def apply(ma: MA): M[A]
implicitly[Unapply[Applicative, Int => Int]].TC.point(0).asInstanceOf[Int => Int](10) assert_=== Applicative[({type l[x]=Function1[Int, x]})#l].point(0)(10)
List(1, 2, 3) traverseU {(x: Int) => {(_:Int) + x}} apply 1 assert_=== List(2, 3, 4) // traverse won't work

Boolean 

false /\ true assert_=== false // &&
false \/ true assert_=== true // ||
(1 < 10) option 1 assert_=== 1.some
(1 > 10)? 1 | 2 assert_=== 2
(1 > 10)?? {List(1)} assert_=== Nil

Option 

1.some assert_=== Some(1)
none[Int] assert_=== (None: Option[Int])
1.some? 'x' | 'y' assert_=== 'x'
1.some | 2 assert_=== 1 // getOrElse

Id[+A] = A 

// no contract function
1 + 2 + 3 |> {_ * 6}
1 visit { case x@(2|3) => List(x * 2) }

Tagged[A] 

sealed trait KiloGram
def KiloGram[A](a: A): A @@ KiloGram = Tag[A, KiloGram](a)
def f[A](mass: A @@ KiloGram): A @@ KiloGram

Tree[A]/TreeLoc[A] 

val tree = 'A'.node('B'.leaf, 'C'.node('D'.leaf), 'E'.leaf)
(tree.loc.getChild(2) >>= {_.getChild(1)} >>= {_.getLabel.some}) assert_=== 'D'.some
(tree.loc.getChild(2) map {_.modifyLabel({_ => 'Z'})}).get.toTree.drawTree assert_=== 'A'.node('B'.leaf, 'Z'.node('D'.leaf), 'E'.leaf).drawTree

Stream[A]/Zipper[A] 

(Stream(1, 2, 3, 4).toZipper >>= {_.next} >>= {_.focus.some}) assert_=== 2.some
(Stream(1, 2, 3, 4).zipperEnd >>= {_.previous} >>= {_.focus.some}) assert_=== 3.some
(for { z <- Stream(1, 2, 3, 4).toZipper; n1 <- z.next } yield { n1.modify {_ => 7} }) map { _.toStream.toList } getOrElse Nil assert_=== List(1, 7, 3, 4)
unfold(3) { x => (x =/= 0) option (x, x - 1) }.toList assert_=== List(3, 2, 1)

DList[A] 

DList.unfoldr(3, { (x: Int) => (x =/= 0) option (x, x - 1) }).toList assert_=== List(3, 2, 1)

Lens[A, B] = LensT[Id, A, B] 

val t0 = Turtle(Point(0.0, 0.0), 0.0)
val t1 = Turtle(Point(1.0, 0.0), 0.0)
val turtlePosition = Lens.lensu[Turtle, Point] (
  (a, value) => a.copy(position = value),
  _.position)
val pointX = Lens.lensu[Point, Double] (
  (a, value) => a.copy(x = value),
  _.x)
val turtleX = turtlePosition >=> pointX
turtleX.get(t0) assert_=== 0.0
turtleX.set(t0, 5.0) assert_=== Turtle(Point(5.0, 0.0), 0.0)
turtleX.mod(_ + 1.0, t0) assert_=== t1
t0 |> (turtleX =>= {_ + 1.0}) assert_=== t1
(for { x <- turtleX %= {_ + 1.0} } yield x) exec t0 assert_=== t1
(for { x <- turtleX := 5.0 } yield x) exec t0 assert_=== Turtle(Point(5.0, 0.0), 0.0)
(for { x <- turtleX += 1.0 } yield x) exec t0 assert_=== t1

Validation[+E, +A] 

(1.success[String] |@| "boom".failure[Int] |@| "boom".failure[Int]) {_ |+| _ |+| _} assert_=== "boomboom".failure[Int]
(1.successNel[String] |@| "boom".failureNel[Int] |@| "boom".failureNel[Int]) {_ |+| _ |+| _} assert_=== NonEmptyList("boom", "boom").failure[Int]
"1".parseInt.toOption assert_=== 1.some

Writer[+W, +A] = WriterT[Id, W, A] 

(for { x <- 1.set("log1"); _ <- "log2".tell } yield (x)).run assert_=== ("log1log2", 1)
import std.vector._
MonadWriter[Writer, Vector[String]].point(1).run assert_=== (Vector(), 1)

\/[+A, +B] 

1.right[String].isRight assert_=== true
1.right[String].isLeft assert_=== false
1.right[String] | 0 assert_=== 1  // getOrElse
("boom".left ||| 2.right) assert_=== 2.right // orElse
("boom".left[Int] >>= { x => (x + 1).right }) assert_=== "boom".left[Int]
(for { e1 <- 1.right; e2 <- "boom".left[Int] } yield (e1 |+| e2)) assert_=== "boom".left[Int]

Kleisli[M[+_], -A, +B] 

val k1 = Kleisli { (x: Int) => (x + 1).some }
val k2 = Kleisli { (x: Int) => (x * 100).some }
(4.some >>= k1 compose k2) assert_=== 401.some
(4.some >>= k1 <=< k2) assert_=== 401.some
(4.some >>= k1 andThen k2) assert_=== 500.some
(4.some >>= k1 >=> k2) assert_=== 500.some

Reader[E, A] = Kleisli[Id, E, A] 

Reader { (_: Int) + 1 }

trait Memo[K, V] 

val memoizedFib: Int => Int = Memo.mutableHashMapMemo {
  case 0 => 0
  case 1 => 1
  case n => memoizedFib(n - 2) + memoizedFib(n - 1)
}

State[S, +A] = StateT[Id, S, A] 

State[List[Int], Int] { case x :: xs => (xs, x) }.run(1 :: Nil) assert_=== (Nil, 1)
(for {
  xs <- get[List[Int]]
  _ <- put(xs.tail)
} yield xs.head).run(1 :: Nil) assert_=== (Nil, 1)

ST[S, A]/STRef[S, A]/STArray[S, A] 

import scalaz._, Scalaz._, effect._, ST._
type ForallST[A] = Forall[({type l[x] = ST[x, A]})#l]
def e1[S]: ST[S, Int] = for {
  x <- newVar[S](0)
  _ <- x mod {_ + 1}
  r <- x.read
} yield r
runST(new ForallST[Int] { def apply[S] = e1[S] }) assert_=== 1
def e2[S]: ST[S, ImmutableArray[Boolean]] = for {
  arr <- newArr[S, Boolean](3, true)
  x <- arr.read(0)
  _ <- arr.write(0, !x)
  r <- arr.freeze
} yield r
runST(new ForallST[ImmutableArray[Boolean]] { def apply[S] = e2[S] })(0) assert_=== false

IO[+A] 

import scalaz._, Scalaz._, effect._, IO._
val action1 = for {
  x <- readLn
  _ <- putStrLn("Hello, " + x + "!")
} yield ()
action1.unsafePerformIO

IterateeT[E, F[_], A]/EnumeratorT[O, I, F[_]] 

import scalaz._, Scalaz._, iteratee._, Iteratee._
(length[Int, Id] &= enumerate(Stream(1, 2, 3))).run assert_=== 3
(length[scalaz.effect.IoExceptionOr[Char], IO] &= enumReader[IO](new BufferedReader(new FileReader("./README.md")))).run.unsafePerformIO

Free[S[+_], +A] 

import scalaz._, Scalaz._, Free._
type FreeMonoid[A] = Free[({type λ[+α] = (A,α)})#λ, Unit]
def cons[A](a: A): FreeMonoid[A] = Suspend[({type λ[+α] = (A,α)})#λ, Unit]((a, Return[({type λ[+α] = (A,α)})#λ, Unit](())))
def toList[A](list: FreeMonoid[A]): List[A] =
  list.resume.fold(
    { case (x: A, xs: FreeMonoid[A]) => x :: toList(xs) },
    { _ => Nil })
toList(cons(1) >>= {_ => cons(2)}) assert_=== List(1, 2)

Trampoline[+A] = Free[Function0, A] 

import scalaz._, Scalaz._, Free._
def even[A](ns: List[A]): Trampoline[Boolean] =
  ns match {
    case Nil => return_(true)
    case x :: xs => suspend(odd(xs))
  }
def odd[A](ns: List[A]): Trampoline[Boolean] =
  ns match {
    case Nil => return_(false)
    case x :: xs => suspend(even(xs))
  }
even(0 |-> 3000).run assert_=== false

Imports 

import scalaz._ // imports type names
import scalaz.Id.Id // imports Id type alias
import scalaz.std.option._ // imports instances, converters, and functions related to `Option`
import scalaz.std.AllInstances._ // imports instances and converters related to standard types
import scalaz.std.AllFunctions._ // imports functions related to standard types
import scalaz.syntax.monad._ // injects operators to Monad
import scalaz.syntax.all._ // injects operators to all typeclasses and Scalaz data types
import scalaz.syntax.std.boolean._ // injects operators to Boolean
import scalaz.syntax.std.all._ // injects operators to all standard types
import scalaz._, Scalaz._ // all the above

Note 

type Function1Int[A] = ({type l[x]=Function1[Int, x]})#l[A]
type Function1Int[A] = Function1[Int, A]