Duality
Opposite category
Before we get into duality, we need to cover the concept of generating a category out of an existing one. Note that we are no longer talking about objects, but a category, which includes objects and arrows.
The opposite (or “dual”) category Cop of a category C has the same objects as C, and an arrow f: C => D in Cop is an arrow f: D => C in C. That is, Cop is just C with all of the arrows formally turned around.
The duality principle
If we take the concept further, we can come up with “dual statement” Σ* by substituting any sentence Σ in the category theory by replacing the following:
- f ∘ g for g ∘ f
- codomain for domain
- domain for codomain
Since there’s nothing semantically important about which side is f or g, the dual statement also holds true as long as Σ only relies on category theory. In other words, any proof that holds for one concept also holds for its dual. This is called the duality principle.
Another way of looking at it is that if Σ holds in all C, it should also hold in Cop, and so Σ* should hold in (Cop)op, which is C.
Let’s look at the definitions of initial and terminal again:
Definition 2.9. In any category C, an object
- 0 is initial if for any object C there is a unique morphism
0 => C- 1 is terminal if for any object C there is a unique morphism
C => 1
They are dual to each other, so the initials in C are terminals in Cop.
Recall proof for “the initial objects are unique up to isomorphism.”
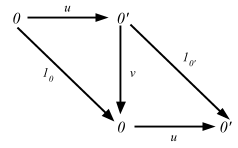
If you flip the direction of all arrows in the above diagram, you do get a proof for terminals.
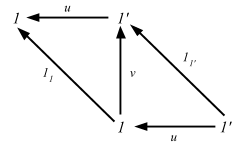
This is pretty cool. Let’s continue from here later.