herding cats 

This is a log of me going through Cats, a functional programming library for Scala. I’ll try to follow the structure of learning Scalaz that I wrote in 2012 (!).

Cats’ website says the name is a playful shortening of the word “category.” Some people say coordinating programmers is like herding cats (as in attempting to move dozens of them in a direction like cattle, while cats have their own ideas), and it seems to be true at least for those of us using Scala. Keenly aware of this situation, the cats list approachability as their first motivation.

Cats also looks interesting from the technical perspective. With its approachability and Erik Asheim (@d6/@non)’s awesomeness, people are gathering around them with new ideas such as Michael Pilquist (@mpilquist)’s simulacrum and Miles Sabin (@milessabin)’s deriving typeclasses. Hopefully I’ll learn more in the coming days.

day 0 

This is a web log of me learning Cats, based a log of me learning Scalaz. It’s sometimes called a tutorial, but you should treat it more like a travel log that was scribbled together. If you want to learn the stuff, I suggest you read books and go through the examples yourself.

Before we dive into the details, here is a prequel to ease you in.

Intro to Cats 

I’m going to borrow material from Nick Partridge’s Scalaz talk given at Melbourne Scala Users Group on March 22, 2010:

Scalaz talk is up - http://bit.ly/c2eTVR Lots of code showing how/why the library exists

— Nick Partridge (@nkpart) March 28, 2010

Cats consists of two parts:

1. New datatypes (Validated, State, etc)
2. Implementation of many general functions you need (ad-hoc polymorphism, traits + implicits)

What is polymorphism? 

Parametric polymorphism 

Nick says:

In this function head, it takes a list of A’s, and returns an A. And it doesn’t matter what the A is: It could be Ints, Strings, Oranges, Cars, whatever. Any A would work, and the function is defined for every A that there can be.

def head[A](xs: List[A]): A = xs(0)
head(1 :: 2 :: Nil)
// res1: Int = 1

case class Car(make: String)
head(Car("Civic") :: Car("CR-V") :: Nil)
// res2: Car = Car(make = "Civic")

Haskell wiki says:

Parametric polymorphism refers to when the type of a value contains one or more (unconstrained) type variables, so that the value may adopt any type that results from substituting those variables with concrete types.

Subtype polymorphism 

Let’s think of a function plus that can add two values of type A:

def plus[A](a1: A, a2: A): A = ???

Depending on the type A, we need to provide different definition for what it means to add them. One way to achieve this is through subtyping.

trait PlusIntf[A] {
  def plus(a2: A): A
}

def plusBySubtype[A <: PlusIntf[A]](a1: A, a2: A): A = a1.plus(a2)

We can at least provide different definitions of plus for A. But, this is not flexible since trait Plus needs to be mixed in at the time of defining the datatype. So it can’t work for Int and String.

Ad-hoc polymorphism 

The third approach in Scala is to provide an implicit conversion or implicit parameters for the trait.

trait CanPlus[A] {
  def plus(a1: A, a2: A): A
}

def plus[A: CanPlus](a1: A, a2: A): A = implicitly[CanPlus[A]].plus(a1, a2)

This is truely ad-hoc in the sense that

1. we can provide separate function definitions for different types of A
2. we can provide function definitions to types (like Int) without access to its source code
3. the function definitions can be enabled or disabled in different scopes

The last point makes Scala’s ad-hoc polymorphism more powerful than that of Haskell. More on this topic can be found at Debasish Ghosh @debasishg’s Scala Implicits : Type Classes Here I Come.

Let’s look into plus function in more detail.

sum function 

Nick demonstrates an example of ad-hoc polymorphism by gradually making sum function more general, starting from a simple function that adds up a list of Ints:

def sum(xs: List[Int]): Int = xs.foldLeft(0) { _ + _ }
sum(List(1, 2, 3, 4))
// res0: Int = 10

Monoid 

If we try to generalize a little bit. I’m going to pull out a thing called Monoid. … It’s a type for which there exists a function mappend, which produces another type in the same set; and also a function that produces a zero.

object IntMonoid {
  def mappend(a: Int, b: Int): Int = a + b
  def mzero: Int = 0
}

If we pull that in, it sort of generalizes what’s going on here:

def sum(xs: List[Int]): Int = xs.foldLeft(IntMonoid.mzero)(IntMonoid.mappend)
sum(List(1, 2, 3, 4))
// res2: Int = 10

Now we’ll abstract on the type about Monoid, so we can define Monoid for any type A. So now IntMonoid is a monoid on Int:

trait Monoid[A] {
  def mappend(a1: A, a2: A): A
  def mzero: A
}
object IntMonoid extends Monoid[Int] {
  def mappend(a: Int, b: Int): Int = a + b
  def mzero: Int = 0
}

What we can do is that sum take a List of Int and a monoid on Int to sum it:

def sum(xs: List[Int], m: Monoid[Int]): Int = xs.foldLeft(m.mzero)(m.mappend)
sum(List(1, 2, 3, 4), IntMonoid)
// res4: Int = 10

We are not using anything to do with Int here, so we can replace all Int with a general type:

def sum[A](xs: List[A], m: Monoid[A]): A = xs.foldLeft(m.mzero)(m.mappend)
sum(List(1, 2, 3, 4), IntMonoid)
// res6: Int = 10

The final change we have to take is to make the Monoid implicit so we don’t have to specify it each time.

def sum[A](xs: List[A])(implicit m: Monoid[A]): A = xs.foldLeft(m.mzero)(m.mappend)

{
  implicit val intMonoid = IntMonoid
  sum(List(1, 2, 3, 4))
}
// res8: Int = 10

Nick didn’t do this, but the implicit parameter is often written as a context bound:

def sum[A: Monoid](xs: List[A]): A = {
  val m = implicitly[Monoid[A]]
  xs.foldLeft(m.mzero)(m.mappend)
}

{
  implicit val intMonoid = IntMonoid
  sum(List(1, 2, 3, 4))
}
// res10: Int = 10

Our sum function is pretty general now, appending any monoid in a list. We can test that by writing another Monoid for String. I’m also going to package these up in an object called Monoid. The reason for that is Scala’s implicit resolution rules: When it needs an implicit parameter of some type, it’ll look for anything in scope. It’ll include the companion object of the type that you’re looking for.

trait Monoid[A] {
  def mappend(a1: A, a2: A): A
  def mzero: A
}
object Monoid {
  implicit val IntMonoid: Monoid[Int] = new Monoid[Int] {
    def mappend(a: Int, b: Int): Int = a + b
    def mzero: Int = 0
  }
  implicit val StringMonoid: Monoid[String] = new Monoid[String] {
    def mappend(a: String, b: String): String = a + b
    def mzero: String = ""
  }
}

def sum[A: Monoid](xs: List[A]): A = {
  val m = implicitly[Monoid[A]]
  xs.foldLeft(m.mzero)(m.mappend)
}
sum(List("a", "b", "c"))
// res12: String = "abc"

You can still provide different monoid directly to the function. We could provide an instance of monoid for Int using multiplications.

val multiMonoid: Monoid[Int] = new Monoid[Int] {
  def mappend(a: Int, b: Int): Int = a * b
  def mzero: Int = 1
}
// multiMonoid: Monoid[Int] = repl.MdocSession3@1dff4342
sum(List(1, 2, 3, 4))(multiMonoid)
// res13: Int = 24

FoldLeft 

What we wanted was a function that generalized on List. … So we want to generalize on foldLeft operation.

object FoldLeftList {
  def foldLeft[A, B](xs: List[A], b: B, f: (B, A) => B) = xs.foldLeft(b)(f)
}
def sum[A: Monoid](xs: List[A]): A = {
  val m = implicitly[Monoid[A]]
  FoldLeftList.foldLeft(xs, m.mzero, m.mappend)
}

sum(List(1, 2, 3, 4))
// res1: Int = 10

sum(List("a", "b", "c"))
// res2: String = "abc"

sum(List(1, 2, 3, 4))(multiMonoid)
// res3: Int = 24

Now we can apply the same abstraction to pull out FoldLeft typeclass.

trait FoldLeft[F[_]] {
  def foldLeft[A, B](xs: F[A], b: B, f: (B, A) => B): B
}
object FoldLeft {
  implicit val FoldLeftList: FoldLeft[List] = new FoldLeft[List] {
    def foldLeft[A, B](xs: List[A], b: B, f: (B, A) => B) = xs.foldLeft(b)(f)
  }
}

def sum[M[_]: FoldLeft, A: Monoid](xs: M[A]): A = {
  val m = implicitly[Monoid[A]]
  val fl = implicitly[FoldLeft[M]]
  fl.foldLeft(xs, m.mzero, m.mappend)
}

sum(List(1, 2, 3, 4))
// res5: Int = 10

sum(List("a", "b", "c"))
// res6: String = "abc"

Both Int and List are now pulled out of sum.

Typeclasses in Cats 

In the above example, the traits Monoid and FoldLeft correspond to Haskell’s typeclass. Cats provides many typeclasses.

All this is broken down into just the pieces you need. So, it’s a bit like ultimate ducktyping because you define in your function definition that this is what you need and nothing more.

Method injection (enrich my library) 

If we were to write a function that sums two types using the Monoid, we need to call it like this.

def plus[A: Monoid](a: A, b: A): A = implicitly[Monoid[A]].mappend(a, b)
plus(3, 4)
// res0: Int = 7

We would like to provide an operator. But we don’t want to enrich just one type, but enrich all types that has an instance for Monoid.

trait Monoid[A] {
  def mappend(a: A, b: A): A
  def mzero: A
}
object Monoid {
  object syntax extends MonoidSyntax

  implicit val IntMonoid: Monoid[Int] = new Monoid[Int] {
    def mappend(a: Int, b: Int): Int = a + b
    def mzero: Int = 0
  }
  implicit val StringMonoid: Monoid[String] = new Monoid[String] {
    def mappend(a: String, b: String): String = a + b
    def mzero: String = ""
  }
}
trait MonoidSyntax {
  implicit final def syntaxMonoid[A: Monoid](a: A): MonoidOps[A] =
    new MonoidOps[A](a)
}
final class MonoidOps[A: Monoid](lhs: A) {
  def |+|(rhs: A): A = implicitly[Monoid[A]].mappend(lhs, rhs)
}

import Monoid.syntax._
3 |+| 4
// res2: Int = 7

"a" |+| "b"
// res3: String = "ab"

We were able to inject |+| to both Int and String with just one definition.

Operator syntax for the standard datatypes 

Using the same technique, Cats occasionally provides method injections for standard library datatypes like Option and Vector:

import cats._, cats.syntax.all._

1.some
// res5: Option[Int] = Some(value = 1)

1.some.orEmpty
// res6: Int = 1

But most operators in Cats are associated with typeclasses.

I hope you could get some feel on where Cats is coming from.

day 1 

typeclasses 101 

Learn You a Haskell for Great Good says:

A typeclass is a sort of interface that defines some behavior. If a type is a part of a typeclass, that means that it supports and implements the behavior the typeclass describes.

Cats says:

We are trying to make the library modular. It will have a tight core which will contain only the typeclasses and the bare minimum of data structures that are needed to support them. Support for using these typeclasses with the Scala standard library will be in the stdproject.

Let’s keep going with learning me a Haskell.

sbt 

Here’s a quick build.sbt to play with Cats:

val catsVersion = "2.4.2"
val catsCore = "org.typelevel" %% "cats-core" % catsVersion
val catsFree = "org.typelevel" %% "cats-free" % catsVersion
val catsLaws = "org.typelevel" %% "cats-laws" % catsVersion
val catsMtl = "org.typelevel" %% "cats-mtl-core" % "0.7.1"

val simulacrum = "org.typelevel" %% "simulacrum" % "1.0.1"
val kindProjector = compilerPlugin("org.typelevel" % "kind-projector" % "0.11.3" cross CrossVersion.full)
val resetAllAttrs = "org.scalamacros" %% "resetallattrs" % "1.0.0"
val munit = "org.scalameta" %% "munit" % "0.7.22"
val disciplineMunit = "org.typelevel" %% "discipline-munit" % "1.0.6"

ThisBuild / scalaVersion := "2.13.5"

lazy val root = (project in file("."))
  .settings(
    organization := "com.example",
    name := "something",
    libraryDependencies ++= Seq(
      catsCore,
      catsFree,
      catsMtl,
      simulacrum,
      kindProjector,
      resetAllAttrs,
      catsLaws % Test,
      munit % Test,
      disciplineMunit % Test,
    ),
    scalacOptions ++= Seq(
      "-deprecation",
      "-encoding", "UTF-8",
      "-feature",
      "-language:_"
    )
  )

You can then open the REPL using sbt 1.4.9:

$ sbt
> console
[info] Starting scala interpreter...
Welcome to Scala 2.13.5 (OpenJDK 64-Bit Server VM, Java 1.8.0_232).
Type in expressions for evaluation. Or try :help.

scala>

There’s also API docs generated for Cats.

Eq 

LYAHFGG:

Eq is used for types that support equality testing. The functions its members implement are == and /=.

Cats’ equivalent for the Eq typeclass is also called Eq. Eq was moved from non/algebra into cats-kernel subproject, and became part of Cats:

import cats._, cats.syntax.all._

1 === 1
// res0: Boolean = true

1 === "foo"
// error: type mismatch;
//  found   : String("foo")
//  required: Int
// 1 === "foo"
//       ^^^^^

(Some(1): Option[Int]) =!= (Some(2): Option[Int])
// res2: Boolean = true

Instead of the standard ==, Eq enables === and =!= syntax by declaring eqv method. The main difference is that === would fail compilation if you tried to compare Int and String.

In algebra, neqv is implemented based on eqv.

/**
 * A type class used to determine equality between 2 instances of the same
 * type. Any 2 instances `x` and `y` are equal if `eqv(x, y)` is `true`.
 * Moreover, `eqv` should form an equivalence relation.
 */
trait Eq[@sp A] extends Any with Serializable { self =>

  /**
   * Returns `true` if `x` and `y` are equivalent, `false` otherwise.
   */
  def eqv(x: A, y: A): Boolean

  /**
   * Returns `false` if `x` and `y` are equivalent, `true` otherwise.
   */
  def neqv(x: A, y: A): Boolean = !eqv(x, y)

  ....
}

This is an example of polymorphism. Whatever equality means for the type A, neqv is the opposite of it. It does not matter if it’s String, Int, or whatever. Another way of looking at it is that given Eq[A], === is universally the opposite of =!=.

I’m a bit concerned that Eq seems to be using the terms “equal” and “equivalent” interchangably. Equivalence relationship could include “having the same birthday” whereas equality also requires substitution property.

Order 

LYAHFGG:

Ord is for types that have an ordering. Ord covers all the standard comparing functions such as >, <, >= and <=.

Cats’ equivalent for the Ord typeclass is Order.

// plain Scala
1 > 2.0
// res0: Boolean = false

import cats._, cats.syntax.all._

1 compare 2.0
// error: type mismatch;
//  found   : Double(2.0)
//  required: Int
// 1.0 compare 2.0
//             ^^^

import cats._, cats.syntax.all._

1.0 compare 2.0
// res2: Int = -1

1.0 max 2.0
// res3: Double = 2.0

Order enables compare syntax which returns Int: negative, zero, or positive. It also enables min and max operators. Similar to Eq, comparing Int and Double fails compilation.

PartialOrder 

In addition to Order, Cats also defines PartialOrder.

import cats._, cats.syntax.all._

1 tryCompare 2
// res0: Option[Int] = Some(value = -1)

1.0 tryCompare Double.NaN
// res1: Option[Int] = Some(value = -1)

PartialOrder enables tryCompare syntax which returns Option[Int]. According to algebra, it’ll return None if operands are not comparable. It’s returning Some(-1) when comparing 1.0 and Double.NaN, so I’m not sure when things are incomparable.

def lt[A: PartialOrder](a1: A, a2: A): Boolean = a1 <= a2
lt(1, 2)
// res2: Boolean = true

lt[Int](1, 2.0)
// error: type mismatch;
//  found   : Double(2.0)
//  required: Int
// lt[Int](1, 2.0)
//            ^^^

PartialOrder also enables >, >=, <, and <= operators, but these are tricky to use because if you’re not careful you could end up using the built-in comparison operators.

Show 

LYAHFGG:

Members of Show can be presented as strings.

Cats’ equivalent for the Show typeclass is Show:

import cats._, cats.syntax.all._

3.show
// res0: String = "3"

"hello".show
// res1: String = "hello"

Here’s the typeclass contract:

@typeclass trait Show[T] {
  def show(f: T): String
}

At first, it might seem silly to define Show because Scala already has toString on Any. Any also means anything would match the criteria, so you lose type safety. The toString could be junk supplied by some parent class:

(new {}).toString
// res2: String = "repl.MdocSession1@891c355"

(new {}).show
// error: value show is not a member of AnyRef
// (new {}).show
//  ^^^^^^^^^^^^

object Show provides two functions to create a Show instance:

object Show {
  /** creates an instance of [[Show]] using the provided function */
  def show[A](f: A => String): Show[A] = new Show[A] {
    def show(a: A): String = f(a)
  }

  /** creates an instance of [[Show]] using object toString */
  def fromToString[A]: Show[A] = new Show[A] {
    def show(a: A): String = a.toString
  }

  implicit val catsContravariantForShow: Contravariant[Show] = new Contravariant[Show] {
    def contramap[A, B](fa: Show[A])(f: B => A): Show[B] =
      show[B](fa.show _ compose f)
  }
}

Let’s try using them:

case class Person(name: String)
case class Car(model: String)

{
  implicit val personShow = Show.show[Person](_.name)
  Person("Alice").show
}
// res4: String = "Alice"

{
  implicit val carShow = Show.fromToString[Car]
  Car("CR-V")
}
// res5: Car = Car(model = "CR-V")

Read 

LYAHFGG:

Read is sort of the opposite typeclass of Show. The read function takes a string and returns a type which is a member of Read.

I could not find Cats’ equivalent for this typeclass.

I find myself defining Read and its variant ReadJs time and time again. Stringly typed programming is ugly. At the same time, String is a robust data format to cross platform boundaries (e.g. JSON). Also we humans know how to deal with them directly (e.g. command line options), so it’s hard to get away from String parsing. If we’re going to do it anyway, having Read makes it easier.

Enum 

LYAHFGG:

Enum members are sequentially ordered types — they can be enumerated. The main advantage of the Enum typeclass is that we can use its types in list ranges. They also have defined successors and predecessors, which you can get with the succ and pred functions.

I could not find Cats’ equivalent for this typeclass.

It’s not an Enum or range, but non/spire has an interesting data structure called Interval. Check out Erik’s Intervals: Unifying Uncertainty, Ranges, and Loops talk from nescala 2015.

Numeric 

LYAHFGG:

Num is a numeric typeclass. Its members have the property of being able to act like numbers.

I could not find Cats’ equivalent for this typeclass, but spire defines Numeric. Cats doesn’t define Bounds either.

So far we’ve seen some of typeclasses that are not defined in Cats. This is not necessarily a bad thing because having a tight core is part of the design goal of Cats.

typeclasses 102 

I am now going to skip over to Chapter 8 Making Our Own Types and Typeclasses (Chapter 7 if you have the book) since the chapters in between are mostly about Haskell syntax.

A traffic light datatype 

data TrafficLight = Red | Yellow | Green

In Scala this would be:

import cats._, cats.syntax.all._

sealed trait TrafficLight
object TrafficLight {
  case object Red extends TrafficLight
  case object Yellow extends TrafficLight
  case object Green extends TrafficLight
}

Now let’s define an instance for Eq.

implicit val trafficLightEq: Eq[TrafficLight] =
  new Eq[TrafficLight] {
    def eqv(a1: TrafficLight, a2: TrafficLight): Boolean = a1 == a2
  }
// trafficLightEq: Eq[TrafficLight] = repl.MdocSession1@124d506d

Note: The latest algebra.Equal includes Equal.instance and Equal.fromUniversalEquals.

Can I use the Eq?

TrafficLight.Red === TrafficLight.Yellow
// error: value === is not a member of object repl.MdocSession.App.TrafficLight.Red
//   TrafficLight.red === TrafficLight.yellow
//   ^^^^^^^^^^^^^^^^^^^^

So apparently Eq[TrafficLight] doesn’t get picked up because Eq has nonvariant subtyping: Eq[A]. One way to workaround this issue is to define helper functions to cast them up to TrafficLight:

import cats._, cats.syntax.all._

sealed trait TrafficLight
object TrafficLight {
  def red: TrafficLight = Red
  def yellow: TrafficLight = Yellow
  def green: TrafficLight = Green
  case object Red extends TrafficLight
  case object Yellow extends TrafficLight
  case object Green extends TrafficLight
}

{
  implicit val trafficLightEq: Eq[TrafficLight] =
    new Eq[TrafficLight] {
      def eqv(a1: TrafficLight, a2: TrafficLight): Boolean = a1 == a2
    }
  TrafficLight.red === TrafficLight.yellow
}
// res2: Boolean = false

It is a bit of boilerplate, but it works.

day 2 

Yesterday we reviewed a few basic typeclasses from Cats like Eq by using Learn You a Haskell for Great Good as the guide.

Making our own typeclass with simulacrum 

LYAHFGG:

In JavaScript and some other weakly typed languages, you can put almost anything inside an if expression. …. Even though strictly using Bool for boolean semantics works better in Haskell, let’s try and implement that JavaScript-ish behavior anyway. For fun!

The conventional steps of defining a modular typeclass in Scala used to look like:

1. Define typeclass contract trait Foo.
2. Define a companion object Foo with a helper method apply that acts like implicitly, and a way of defining Foo instances typically from a function.
3. Define FooOps class that defines unary or binary operators.
4. Define FooSyntax trait that implicitly provides FooOps from a Foo instance.

Frankly, these steps are mostly copy-paste boilerplate except for the first one. Enter Michael Pilquist (@mpilquist)’s simulacrum. simulacrum magically generates most of steps 2-4 just by putting @typeclass annotation. By chance, Stew O’Connor (@stewoconnor/@stew)’s #294 got merged, which refactors Cats to use it.

Yes-No typeclass 

In any case, let’s see if we can make our own truthy value typeclass. Note the @typeclass annotation:

scala> import simulacrum._
scala> :paste
@typeclass trait CanTruthy[A] { self =>
  /** Return true, if `a` is truthy. */
  def truthy(a: A): Boolean
}
object CanTruthy {
  def fromTruthy[A](f: A => Boolean): CanTruthy[A] = new CanTruthy[A] {
    def truthy(a: A): Boolean = f(a)
  }
}

According to the README, the macro will generate all the operator enrichment stuff:

// This is the supposed generated code. You don't have to write it!
object CanTruthy {
  def fromTruthy[A](f: A => Boolean): CanTruthy[A] = new CanTruthy[A] {
    def truthy(a: A): Boolean = f(a)
  }

  def apply[A](implicit instance: CanTruthy[A]): CanTruthy[A] = instance

  trait Ops[A] {
    def typeClassInstance: CanTruthy[A]
    def self: A
    def truthy: A = typeClassInstance.truthy(self)
  }

  trait ToCanTruthyOps {
    implicit def toCanTruthyOps[A](target: A)(implicit tc: CanTruthy[A]): Ops[A] = new Ops[A] {
      val self = target
      val typeClassInstance = tc
    }
  }

  trait AllOps[A] extends Ops[A] {
    def typeClassInstance: CanTruthy[A]
  }

  object ops {
    implicit def toAllCanTruthyOps[A](target: A)(implicit tc: CanTruthy[A]): AllOps[A] = new AllOps[A] {
      val self = target
      val typeClassInstance = tc
    }
  }
}

To make sure it works, let’s define an instance for Int and use it. The eventual goal is to get 1.truthy to return true:

scala> implicit val intCanTruthy: CanTruthy[Int] = CanTruthy.fromTruthy({
         case 0 => false
         case _ => true
       })
scala> import CanTruthy.ops._
scala> 10.truthy

It works. This is quite nifty. One caveat is that this requires Macro Paradise plugin to compile. Once it’s compiled the user of CanTruthy can use it without Macro Paradise.

Symbolic operators 

For CanTruthy the injected operator happened to be unary, and it matched the name of the function on the typeclass contract. simulacrum can also define operator with symbolic names using @op annotation:

scala> @typeclass trait CanAppend[A] {
  @op("|+|") def append(a1: A, a2: A): A
}
scala> implicit val intCanAppend: CanAppend[Int] = new CanAppend[Int] {
  def append(a1: Int, a2: Int): Int = a1 + a2
}
scala> import CanAppend.ops._
scala> 1 |+| 2

Functor 

LYAHFGG:

And now, we’re going to take a look at the Functor typeclass, which is basically for things that can be mapped over.

Like the book let’s look how it's implemented:

/**
 * Functor.
 *
 * The name is short for "covariant functor".
 *
 * Must obey the laws defined in cats.laws.FunctorLaws.
 */
@typeclass trait Functor[F[_]] extends functor.Invariant[F] { self =>
  def map[A, B](fa: F[A])(f: A => B): F[B]

  ....
}

Here’s how we can use this:

import cats._, cats.syntax.all._

Functor[List].map(List(1, 2, 3)) { _ + 1 }
// res0: List[Int] = List(2, 3, 4)

Let’s call the above usage the function syntax.

We now know that @typeclass annotation will automatically turn a map function into a map operator. The fa part turns into the this of the method, and the second parameter list will now be the parameter list of map operator:

// Supposed generated code
object Functor {
  trait Ops[F[_], A] {
    def typeClassInstance: Functor[F]
    def self: F[A]
    def map[B](f: A => B): F[B] = typeClassInstance.map(self)(f)
  }
}

This looks almost like the map method on Scala collection library, except this map doesn’t do the CanBuildFrom auto conversion.

Either as a functor 

Cats defines a Functor instance for Either[A, B].

(Right(1): Either[String, Int]) map { _ + 1 }
// res1: Either[String, Int] = Right(value = 2)

(Left("boom!"): Either[String, Int]) map { _ + 1 }
// res2: Either[String, Int] = Left(value = "boom!")

Note that the above demonstration only works because Either[A, B] at the moment does not implement its own map. If I used List(1, 2, 3) it will call List’s implementation of map instead of the Functor[List]’s map. Therefore, even though the operator syntax looks familiar, we should either avoid using it unless you’re sure that standard library doesn’t implement the map or you’re using it from a polymorphic function. One workaround is to opt for the function syntax.

Function as a functor 

Cats also defines a Functor instance for Function1.

{
  val addOne: Int => Int = (x: Int) => x + 1
  val h: Int => Int = addOne map {_ * 7}
  h(3)
}
// res3: Int = 28

This is interesting. Basically map gives us a way to compose functions, except the order is in reverse from f compose g. Another way of looking at Function1 is that it’s an infinite map from the domain to the range. Now let’s skip the input and output stuff and go to Functors, Applicative Functors and Monoids.

How are functions functors? …

What does the type fmap :: (a -> b) -> (r -> a) -> (r -> b) for this instance tell us? Well, we see that it takes a function from a to b and a function from r to a and returns a function from r to b. Does this remind you of anything? Yes! Function composition!

Oh man, LYAHFGG came to the same conclusion as I did about the function composition. But wait…

ghci> fmap (*3) (+100) 1
303
ghci> (*3) . (+100) $ 1
303

In Haskell, the fmap seems to be working in the same order as f compose g. Let’s check in Scala using the same numbers:

{
  (((_: Int) * 3) map {_ + 100}) (1)
}
// res4: Int = 103

Something is not right. Let’s compare the declaration of fmap and Cats’ map function:

fmap :: (a -> b) -> f a -> f b

and here’s Cats:

def map[A, B](fa: F[A])(f: A => B): F[B]

So the order is flipped. Here’s Paolo Giarrusso (@blaisorblade)’s explanation:

That’s a common Haskell-vs-Scala difference.

In Haskell, to help with point-free programming, the “data” argument usually comes last. For instance, I can write map f . map g . map h and get a list transformer, because the argument order is map f list. (Incidentally, map is an restriction of fmap to the List functor).

In Scala instead, the “data” argument is usually the receiver. That’s often also important to help type inference, so defining map as a method on functions would not bring you very far: think the mess Scala type inference would make of (x => x + 1) map List(1, 2, 3).

This seems to be the popular explanation.

Lifting a function 

LYAHFGG:

[We can think of fmap as] a function that takes a function and returns a new function that’s just like the old one, only it takes a functor as a parameter and returns a functor as the result. It takes an a -> b function and returns a function f a -> f b. This is called lifting a function.

ghci> :t fmap (*2)
fmap (*2) :: (Num a, Functor f) => f a -> f a
ghci> :t fmap (replicate 3)
fmap (replicate 3) :: (Functor f) => f a -> f [a]

If the parameter order has been flipped, are we going to miss out on this lifting goodness? Fortunately, Cats implements derived functions under the Functor typeclass:

@typeclass trait Functor[F[_]] extends functor.Invariant[F] { self =>
  def map[A, B](fa: F[A])(f: A => B): F[B]

  ....

  // derived methods

  /**
   * Lift a function f to operate on Functors
   */
  def lift[A, B](f: A => B): F[A] => F[B] = map(_)(f)

  /**
   * Empty the fa of the values, preserving the structure
   */
  def void[A](fa: F[A]): F[Unit] = map(fa)(_ => ())

  /**
   * Tuple the values in fa with the result of applying a function
   * with the value
   */
  def fproduct[A, B](fa: F[A])(f: A => B): F[(A, B)] = map(fa)(a => a -> f(a))

  /**
   * Replaces the `A` value in `F[A]` with the supplied value.
   */
  def as[A, B](fa: F[A], b: B): F[B] = map(fa)(_ => b)
}

As you see, we have lift!

{
  val lifted = Functor[List].lift {(_: Int) * 2}
  lifted(List(1, 2, 3))
}
// res5: List[Int] = List(2, 4, 6)

We’ve just lifted the function {(_: Int) * 2} to List[Int] => List[Int]. Here the other derived functions using the operator syntax:

List(1, 2, 3).void
// res6: List[Unit] = List((), (), ())

List(1, 2, 3) fproduct {(_: Int) * 2}
// res7: List[(Int, Int)] = List((1, 2), (2, 4), (3, 6))

List(1, 2, 3) as "x"
// res8: List[String] = List("x", "x", "x")

Functor Laws 

LYAHFGG:

In order for something to be a functor, it should satisfy some laws. All functors are expected to exhibit certain kinds of functor-like properties and behaviors. … The first functor law states that if we map the id function over a functor, the functor that we get back should be the same as the original functor.

We can check this for Either[A, B].

val x: Either[String, Int] = Right(1)
// x: Either[String, Int] = Right(value = 1)

assert { (x map identity) === x }

The second law says that composing two functions and then mapping the resulting function over a functor should be the same as first mapping one function over the functor and then mapping the other one.

In other words,

val f = {(_: Int) * 3}
// f: Int => Int = <function1>

val g = {(_: Int) + 1}
// g: Int => Int = <function1>

assert { (x map (f map g)) === (x map f map g) }

These are laws the implementer of the functors must abide, and not something the compiler can check for you.

Checking laws with Discipline 

The compiler can’t check for the laws, but Cats ships with a FunctorLaws trait that describes this in code:

/**
 * Laws that must be obeyed by any [[Functor]].
 */
trait FunctorLaws[F[_]] extends InvariantLaws[F] {
  implicit override def F: Functor[F]

  def covariantIdentity[A](fa: F[A]): IsEq[F[A]] =
    fa.map(identity) <-> fa

  def covariantComposition[A, B, C](fa: F[A], f: A => B, g: B => C): IsEq[F[C]] =
    fa.map(f).map(g) <-> fa.map(f andThen g)
}

Checking laws from the REPL 

This is based on a library called Discipline, which is a wrapper around ScalaCheck. We can run these tests from the REPL with ScalaCheck.

scala> import cats._, cats.syntax.all._
import cats._
import cats.syntax.all._

scala> import cats.laws.discipline.FunctorTests
import cats.laws.discipline.FunctorTests

scala> val rs = FunctorTests[Either[Int, *]].functor[Int, Int, Int]
val rs: cats.laws.discipline.FunctorTests[[?$0$]scala.util.Either[Int,?$0$]]#RuleSet = org.typelevel.discipline.Laws$DefaultRuleSet@2b1a2a1d

scala> import org.scalacheck.Test.Parameters
import org.scalacheck.Test.Parameters

scala> rs.all.check(Parameters.default)
+ functor.covariant composition: OK, passed 100 tests.
+ functor.covariant identity: OK, passed 100 tests.
+ functor.invariant composition: OK, passed 100 tests.
+ functor.invariant identity: OK, passed 100 tests.

rs.all returns org.scalacheck.Properties, which implements check method.

Checking laws with Discipline + MUnit 

In addition to ScalaCheck, you can call these tests from ScalaTest, Specs2, or MUnit. An MUnit test to check the functor law for Either[Int, Int] looks like this:

package example

import cats._
import cats.laws.discipline.FunctorTests

class EitherTest extends munit.DisciplineSuite {
  checkAll("Either[Int, Int]", FunctorTests[Either[Int, *]].functor[Int, Int, Int])
}

The Either[Int, *] is using non/kind-projector. Running the test from sbt displays the following output:

sbt:herding-cats> Test/testOnly example.EitherTest
example.EitherTest:
  + Either[Int, Int]: functor.covariant composition 0.096s
  + Either[Int, Int]: functor.covariant identity 0.017s
  + Either[Int, Int]: functor.invariant composition 0.041s
  + Either[Int, Int]: functor.invariant identity 0.011s
[info] Passed: Total 4, Failed 0, Errors 0, Passed 4

Breaking the law 

LYAHFGG:

Let’s take a look at a pathological example of a type constructor being an instance of the Functor typeclass but not really being a functor, because it doesn’t satisfy the laws.

Let’s try breaking the law.

package example

import cats._

sealed trait COption[+A]
case class CSome[A](counter: Int, a: A) extends COption[A]
case object CNone extends COption[Nothing]

object COption {
  implicit def coptionEq[A]: Eq[COption[A]] = new Eq[COption[A]] {
    def eqv(a1: COption[A], a2: COption[A]): Boolean = a1 == a2
  }
  implicit val coptionFunctor = new Functor[COption] {
    def map[A, B](fa: COption[A])(f: A => B): COption[B] =
      fa match {
        case CNone => CNone
        case CSome(c, a) => CSome(c + 1, f(a))
      }
  }
}

Here’s how we can use this:

import cats._, cats.syntax.all._
import example._

(CSome(0, "hi"): COption[String]) map {identity}
// res0: COption[String] = CSome(counter = 1, a = "hi")

This breaks the first law because the result of the identity function is not equal to the input. To catch this we need to supply an “arbitrary” COption[A] implicitly:

package example

import cats._
import cats.laws.discipline.{ FunctorTests }
import org.scalacheck.{ Arbitrary, Gen }

class COptionTest extends munit.DisciplineSuite {
  checkAll("COption[Int]", FunctorTests[COption].functor[Int, Int, Int])

  implicit def coptionArbiterary[A](implicit arbA: Arbitrary[A]): Arbitrary[COption[A]] =
    Arbitrary {
      val arbSome = for {
        i <- implicitly[Arbitrary[Int]].arbitrary
        a <- arbA.arbitrary
      } yield (CSome(i, a): COption[A])
      val arbNone = Gen.const(CNone: COption[Nothing])
      Gen.oneOf(arbSome, arbNone)
    }
}

Here’s the output:

example.COptionTest:
failing seed for functor.covariant composition is 43LA3KHokN6KnEAzbkXi6IijQU91ran9-zsO2JeIyIP=
==> X example.COptionTest.COption[Int]: functor.covariant composition  0.058s munit.FailException: /Users/eed3si9n/work/herding-cats/src/test/scala/example/COptionTest.scala:8
7:class COptionTest extends munit.DisciplineSuite {
8:  checkAll("COption[Int]", FunctorTests[COption].functor[Int, Int, Int])
9:

Failing seed: 43LA3KHokN6KnEAzbkXi6IijQU91ran9-zsO2JeIyIP=
You can reproduce this failure by adding the following override to your suite:

  override val scalaCheckInitialSeed = "43LA3KHokN6KnEAzbkXi6IijQU91ran9-zsO2JeIyIP="

Falsified after 0 passed tests.
> Labels of failing property:
Expected: CSome(2,-1)
Received: CSome(3,-1)
> ARG_0: CSome(1,0)
> ARG_1: org.scalacheck.GenArities$$Lambda$36505/1702985322@62d7d97c
> ARG_2: org.scalacheck.GenArities$$Lambda$36505/1702985322@18bdc9d7
    ....
failing seed for functor.covariant identity is a4C-NCiCQEn0lU6F_TXdy5-IZ-XhMYDrC0vipJ3O_tG=
==> X example.COptionTest.COption[Int]: functor.covariant identity  0.003s munit.FailException: /Users/eed3si9n/work/herding-cats/src/test/scala/example/COptionTest.scala:8
7:class COptionTest extends munit.DisciplineSuite {
8:  checkAll("COption[Int]", FunctorTests[COption].functor[Int, Int, Int])
9:

Failing seed: RhjRyflmRS-5CYveyf0uAFHuX6mWNm-Z98FVIs2aIVC=
You can reproduce this failure by adding the following override to your suite:

  override val scalaCheckInitialSeed = "RhjRyflmRS-5CYveyf0uAFHuX6mWNm-Z98FVIs2aIVC="

Falsified after 1 passed tests.
> Labels of failing property:
Expected: CSome(-1486306630,-1498342842)
Received: CSome(-1486306629,-1498342842)
> ARG_0: CSome(-1486306630,-1498342842)
    ....
failing seed for functor.invariant composition is 9uQIZNNK_uZksfWg5pRb0VJUIgUtkv9vG9ckZ4UlRwD=
==> X example.COptionTest.COption[Int]: functor.invariant composition  0.005s munit.FailException: /Users/eed3si9n/work/herding-cats/src/test/scala/example/COptionTest.scala:8
7:class COptionTest extends munit.DisciplineSuite {
8:  checkAll("COption[Int]", FunctorTests[COption].functor[Int, Int, Int])
9:

Failing seed: 9uQIZNNK_uZksfWg5pRb0VJUIgUtkv9vG9ckZ4UlRwD=
You can reproduce this failure by adding the following override to your suite:

  override val scalaCheckInitialSeed = "9uQIZNNK_uZksfWg5pRb0VJUIgUtkv9vG9ckZ4UlRwD="

Falsified after 0 passed tests.
> Labels of failing property:
Expected: CSome(1,2147483647)
Received: CSome(2,2147483647)
> ARG_0: CSome(0,1095768235)
> ARG_1: org.scalacheck.GenArities$$Lambda$36505/1702985322@431263ab
> ARG_2: org.scalacheck.GenArities$$Lambda$36505/1702985322@5afe6566
> ARG_3: org.scalacheck.GenArities$$Lambda$36505/1702985322@ca0deda
> ARG_4: org.scalacheck.GenArities$$Lambda$36505/1702985322@1d7dde37
    ....
failing seed for functor.invariant identity is RcktTeI0rbpoUfuI3FHdvZtVGXGMoAjB6JkNBcTNTVK=
==> X example.COptionTest.COption[Int]: functor.invariant identity  0.002s munit.FailException: /Users/eed3si9n/work/herding-cats/src/test/scala/example/COptionTest.scala:8
7:class COptionTest extends munit.DisciplineSuite {
8:  checkAll("COption[Int]", FunctorTests[COption].functor[Int, Int, Int])
9:

Failing seed: RcktTeI0rbpoUfuI3FHdvZtVGXGMoAjB6JkNBcTNTVK=
You can reproduce this failure by adding the following override to your suite:

  override val scalaCheckInitialSeed = "RcktTeI0rbpoUfuI3FHdvZtVGXGMoAjB6JkNBcTNTVK="

Falsified after 0 passed tests.
> Labels of failing property:
Expected: CSome(2147483647,1054398067)
Received: CSome(-2147483648,1054398067)
> ARG_0: CSome(2147483647,1054398067)
    ....
[error] Failed: Total 4, Failed 4, Errors 0, Passed 0
[error] Failed tests:
[error]   example.COptionTest
[error] (Test / testOnly) sbt.TestsFailedException: Tests unsuccessful

The tests failed as expected.

Import guide 

Cats makes heavy use of implicits. Both as a user and an extender of the library, it will be useful to have general idea on where things are coming from. If you’re just starting out with Cats, you can use the following the imports and skip this page, assuming you’re using Cats 2.2.0 and above:

scala> import cats._, cats.data._, cats.syntax.all._

Prior to Cats 2.2.0 it was:

scala> import cats._, cats.data._, cats.implicits._

Implicits review 

Let’s quickly review Scala 2’s imports and implicits! In Scala, imports are used for two purposes:

1. To include names of values and types into the scope.
2. To include implicits into the scope.

Given some type A, implicit is a mechanism to ask the compiler for a specific (term) value for the type. This can be used for different purposes, for Cats, the 2 main usages are:

1. instances; to provide typeclass instances.
2. syntax; to inject methods and operators. (method extension)

Implicits are selected in the following precedence:

1. Values and converters accessible without prefix via local declaration, imports, outer scope, inheritance, and current package object. Inner scope can shadow values when they are named the same.
2. Implicit scope. Values and converters declared in companion objects and package object of the type, its parts, or super types.

import cats._ 

Now let’s see what gets imported with import cats._.

First, the names. Typeclasses like Show[A] and Functor[F[_]] are implemented as trait, and are defined under the cats package. So instead of writing cats.Show[A] we can write Show[A].

Next, also the names, but type aliases. cats’s package object declares type aliases like Eq[A] and ~>[F[_], G[_]]. Again, these can also be accessed as cats.Eq[A] if you want.

Finally, catsInstancesForId is defined as typeclass instance of Id[A] for Traverse[F[_]], Monad[F[_]] etc, but it’s not relevant. By virtue of declaring an instance within its package object it will be available, so importing doesn’t add much. Let’s check this:

scala> cats.Functor[cats.Id]
res0: cats.Functor[cats.Id] = cats.package$$anon$1@3c201c09

No import needed, which is a good thing. So, the merit of import cats._ is for convenience, and it’s optional.

Implicit scope 

In March 2020, Travis Brown’s #3043 was merged and was released as Cats 2.2.0. In short, this change added the typeclass instances of standard library types into the companion object of the typeclasses.

This reduces the need for importing things into the lexical scope, which has the benefit of simplicity and apparently less work for the compiler. For instance, with Cats 2.4.x the following works without any imports:

scala> cats.Functor[Option]
val res1: cats.Functor[Option] = cats.instances.OptionInstances$$anon$1@56a2a3bf

See Travis’s Implicit scope and Cats for more details.

import cats.data._ 

Next let’s see what gets imported with import cats.data._.

First, more names. There are custom datatype defined under the cats.data package such as Validated[+E, +A].

Next, the type aliases. The cats.data package object defines type aliases such as Reader[A, B], which is treated as a specialization of ReaderT transformer. We can still write this as cats.data.Reader[A, B].

import cats.implicits._ 

What then is import cats.implicits._ doing? Here’s the definition of implicits object:

package cats

object implicits extends syntax.AllSyntax with instances.AllInstances

This is quite a nice way of organizing the imports. implicits object itself doesn’t define anythig and it just mixes in the traits. We are going to look at each traits in detail, but they can also be imported a la carte, dim sum style. Back to the full course.

cats.instances.AllInstances 

Thus far, I have been intentionally conflating the concept of typeclass instances and method injection (aka enrich my library). But the fact that (Int, +) forms a Monoid and that Monoid introduces |+| operator are two different things.

One of the interesting design of Cats is that it rigorously separates the two concepts into “instance” and “syntax.” Even if it makes logical sense to some users, the choice of symbolic operators can often be a point of contention with any libraries. Libraries and tools such as sbt, dispatch, and specs introduce its own DSL, and their effectiveness have been hotly debated.

AllInstances is a trait that mixes in all the typeclass instances for built-in datatypes such as Either[A, B] and Option[A].

package cats
package instances

trait AllInstances
  extends FunctionInstances
  with    StringInstances
  with    EitherInstances
  with    ListInstances
  with    OptionInstances
  with    SetInstances
  with    StreamInstances
  with    VectorInstances
  with    AnyValInstances
  with    MapInstances
  with    BigIntInstances
  with    BigDecimalInstances
  with    FutureInstances
  with    TryInstances
  with    TupleInstances
  with    UUIDInstances
  with    SymbolInstances

cats.syntax.AllSyntax 

AllSyntax is a trait that mixes in all of the operators available in Cats.

package cats
package syntax

trait AllSyntax
    extends ApplicativeSyntax
    with ApplicativeErrorSyntax
    with ApplySyntax
    with BifunctorSyntax
    with BifoldableSyntax
    with BitraverseSyntax
    with CartesianSyntax
    with CoflatMapSyntax
    with ComonadSyntax
    with ComposeSyntax
    with ContravariantSyntax
    with CoproductSyntax
    with EitherSyntax
    with EqSyntax
    ....

a la carte style 

Or, I’d like to call dim sum style, where they bring in a cart load of chinese dishes and you pick what you want.

If for whatever reason if you do not wish to import the entire cats.implicits._, you can pick and choose.

typeclass instances 

As I mentioned above, after Cats 2.2.0, you typically don’t have to do anything to get the typeclass instances.

cats.Monad[Option].pure(0)
// res0: Option[Int] = Some(value = 0)

If you want to import typeclass instances for Option for some reason:

{
  import cats.instances.option._
  cats.Monad[Option].pure(0)
}
// res1: Option[Int] = Some(value = 0)

If you just want all instances, here’s how to load them all:

{
  import cats.instances.all._
  cats.Monoid[Int].empty
}
// res2: Int = 0

Because we have not injected any operators, you would have to work more with helper functions and functions under typeclass instances, which could be exactly what you want.

Cats typeclass syntax 

Typeclass syntax are broken down by the typeclass. Here’s how to get injected methods and operators for Eqs:

{
  import cats.syntax.eq._
  1 === 1
}
// res3: Boolean = true

Cats datatype syntax 

Cats datatype syntax like Writer are also available under cats.syntax package:

{
  import cats.syntax.writer._
  1.tell
}
// res4: cats.data.package.Writer[Int, Unit] = WriterT(run = (1, ()))

standard datatype syntax 

Standard datatype syntax are broken down by the datatypes. Here’s how to get injected methods and functions for Option:

{
  import cats.syntax.option._
  1.some
}
// res5: Option[Int] = Some(value = 1)

all syntax 

Here’s how to load all syntax and all instances.

{
  import cats.syntax.all._
  import cats.instances.all._
  1.some
}
// res6: Option[Int] = Some(value = 1)

This is the same as importing cats.implicits._. Again, if you are at all confused by this, just stick with the following first:

scala> import cats._, cats.data._, cats.syntax.all._

day 3 

Yesterday we started with defining our own typeclasses using simulacrum, and ended with checking for functor laws using Discipline.

Kinds and some type-foo 

Learn You a Haskell For Great Good says:

Types are little labels that values carry so that we can reason about the values. But types have their own little labels, called kinds. A kind is more or less the type of a type. … What are kinds and what are they good for? Well, let’s examine the kind of a type by using the :k command in GHCI.

Scala 2.10 didn’t have a :k command, so I wrote kind.scala. Thanks to George Leontiev (@folone) and others, :kind command is now part of Scala 2.11 (scala/scala#2340). Let’s try using it:

scala> :k Int
scala.Int's kind is A

scala> :k -v Int
scala.Int's kind is A
*
This is a proper type.

Int and every other types that you can make a value out of are called a proper type and denoted with a * symbol (read “type”). This is analogous to the value 1 at value-level. Using Scala’s type variable notation this could be written as A.

scala> :k -v Option
scala.Option's kind is F[+A]
* -(+)-> *
This is a type constructor: a 1st-order-kinded type.

scala> :k -v Either
scala.util.Either's kind is F[+A1,+A2]
* -(+)-> * -(+)-> *
This is a type constructor: a 1st-order-kinded type.

These are normally called type constructors. Another way of looking at it is that it’s one step removed from a proper type. So we can call it a first-order-kinded type. This is analogous to a first-order value (_: Int) + 3, which we would normally call a function at the value level.

The curried notation uses arrows like * -> * and * -> * -> *. Note, Option[Int] is *; Option is * -> *. Using Scala’s type variable notation they could be written as F[+A] and F[+A1,+A2].

scala> :k -v Eq
algebra.Eq's kind is F[A]
* -> *
This is a type constructor: a 1st-order-kinded type.

Scala encodes (or complects) the notion of typeclasses using type constructors. When looking at this, think of it as Eq is a typeclass for A, a proper type. This should make sense because you would pass Int into Eq.

scala> :k -v Functor
cats.Functor's kind is X[F[A]]
(* -> *) -> *
This is a type constructor that takes type constructor(s): a higher-kinded type.

Again, Scala encodes typeclasses using type constructors, so when looking at this, think of it as Functor is a typeclass for F[A], a type constructor. This should also make sense because you would pass List into Functor.

In other words, this is a type constructor that accepts another type constructor. This is analogous to a higher-order function, and thus called higher-kinded type. These are denoted as (* -> *) -> *. Using Scala’s type variable notation this could be written as X[F[A]].

forms-a vs is-a 

The terminology around typeclasses tends to get jumbled up. For example, the pair (Int, +) forms a typeclass called monoid. Colloquially, we say things like “is X a monoid?” to mean “can X form a monoid under some operation?”

An example of this is Either[A, B], which we implied “is-a” functor yesterday. This is not completely accurate because, even though it might not be useful, we could have defined another left-biased functor.

Semigroupal 

Functors, Applicative Functors and Monoids:

So far, when we were mapping functions over functors, we usually mapped functions that take only one parameter. But what happens when we map a function like *, which takes two parameters, over a functor?

import cats._

{
  val hs = Functor[List].map(List(1, 2, 3, 4)) ({(_: Int) * (_:Int)}.curried)
  Functor[List].map(hs) {_(9)}
}
// res0: List[Int] = List(9, 18, 27, 36)

LYAHFGG:

But what if we have a functor value of Just (3 *) and a functor value of Just 5, and we want to take out the function from Just(3 *) and map it over Just 5?

Meet the Applicative typeclass. It lies in the Control.Applicative module and it defines two methods, pure and <*>.

Cats splits this into Semigroupal, Apply, and Applicative. Here’s the contract for Cartesian:

/**
 * [[Semigroupal]] captures the idea of composing independent effectful values.
 * It is of particular interest when taken together with [[Functor]] - where [[Functor]]
 * captures the idea of applying a unary pure function to an effectful value,
 * calling `product` with `map` allows one to apply a function of arbitrary arity to multiple
 * independent effectful values.
 *
 * That same idea is also manifested in the form of [[Apply]], and indeed [[Apply]] extends both
 * [[Semigroupal]] and [[Functor]] to illustrate this.
 */
@typeclass trait Semigroupal[F[_]] {
  def product[A, B](fa: F[A], fb: F[B]): F[(A, B)]
}

Semigroupal defines product function, which produces a pair of (A, B) wrapped in effect F[_] out of F[A] and F[B].

Cartesian law 

Cartesian has a single law called associativity:

trait CartesianLaws[F[_]] {
  implicit def F: Cartesian[F]

  def cartesianAssociativity[A, B, C](fa: F[A], fb: F[B], fc: F[C]): (F[(A, (B, C))], F[((A, B), C)]) =
    (F.product(fa, F.product(fb, fc)), F.product(F.product(fa, fb), fc))
}

Apply 

Functors, Applicative Functors and Monoids:

So far, when we were mapping functions over functors, we usually mapped functions that take only one parameter. But what happens when we map a function like *, which takes two parameters, over a functor?

import cats._, cats.syntax.all._

{
  val hs = Functor[List].map(List(1, 2, 3, 4)) ({(_: Int) * (_:Int)}.curried)
  Functor[List].map(hs) {_(9)}
}
// res0: List[Int] = List(9, 18, 27, 36)

LYAHFGG:

But what if we have a functor value of Just (3 *) and a functor value of Just 5, and we want to take out the function from Just(3 *) and map it over Just 5?

Meet the Applicative typeclass. It lies in the Control.Applicative module and it defines two methods, pure and <*>.

Cats splits Applicative into Cartesian, Apply, and Applicative. Here’s the contract for Apply:

/**
 * Weaker version of Applicative[F]; has apply but not pure.
 *
 * Must obey the laws defined in cats.laws.ApplyLaws.
 */
@typeclass(excludeParents = List("ApplyArityFunctions"))
trait Apply[F[_]] extends Functor[F] with Cartesian[F] with ApplyArityFunctions[F] { self =>

  /**
   * Given a value and a function in the Apply context, applies the
   * function to the value.
   */
  def ap[A, B](ff: F[A => B])(fa: F[A]): F[B]

  ....
}

Note that Apply extends Functor, Cartesian, and ApplyArityFunctions. The <*> function is called ap in Cats’ Apply. (This was originally called apply, but was renamed to ap. +1)

LYAHFGG:

You can think of <*> as a sort of a beefed-up fmap. Whereas fmap takes a function and a functor and applies the function inside the functor value, <*> takes a functor that has a function in it and another functor and extracts that function from the first functor and then maps it over the second one.

The Applicative Style 

LYAHFGG:

With the Applicative type class, we can chain the use of the <*> function, thus enabling us to seamlessly operate on several applicative values instead of just one.

Here’s an example in Haskell:

ghci> pure (-) <*> Just 3 <*> Just 5
Just (-2)

Cats comes with the apply syntax.

(3.some, 5.some) mapN { _ - _ }
// res1: Option[Int] = Some(value = -2)

(none[Int], 5.some) mapN { _ - _ }
// res2: Option[Int] = None

(3.some, none[Int]) mapN { _ - _ }
// res3: Option[Int] = None

This shows that Option forms Cartesian.

List as a Apply 

LYAHFGG:

Lists (actually the list type constructor, []) are applicative functors. What a surprise!

Let’s see if we can use the apply sytax:

(List("ha", "heh", "hmm"), List("?", "!", ".")) mapN {_ + _}
// res4: List[String] = List(
//   "ha?",
//   "ha!",
//   "ha.",
//   "heh?",
//   "heh!",
//   "heh.",
//   "hmm?",
//   "hmm!",
//   "hmm."
// )

*> and <* operators 

Apply enables two operators, <* and *>, which are special cases of Apply[F].map2。

The definition looks simple enough, but the effect is cool:

1.some <* 2.some
// res5: Option[Int] = Some(value = 1)

none[Int] <* 2.some
// res6: Option[Int] = None

1.some *> 2.some
// res7: Option[Int] = Some(value = 2)

none[Int] *> 2.some
// res8: Option[Int] = None

If either side fails, we get None.

Option syntax 

Before we move on, let’s look at the syntax that Cats adds to create an Option value.

9.some
// res9: Option[Int] = Some(value = 9)

none[Int]
// res10: Option[Int] = None

We can write (Some(9): Option[Int]) as 9.some.

Option as an Apply 

Here’s how we can use it with Apply[Option].ap:

import cats._, cats.syntax.all._

Apply[Option].ap({{(_: Int) + 3}.some })(9.some)
// res12: Option[Int] = Some(value = 12)

Apply[Option].ap({{(_: Int) + 3}.some })(10.some)
// res13: Option[Int] = Some(value = 13)

Apply[Option].ap({{(_: String) + "hahah"}.some })(none[String])
// res14: Option[String] = None

Apply[Option].ap({ none[String => String] })("woot".some)
// res15: Option[String] = None

If either side fails, we get None.

If you remember Making our own typeclass with simulacrum from yesterday, simulacrum will automatically transpose the function defined on the typeclass contract into an operator, magically.

({(_: Int) + 3}.some) ap 9.some
// res16: Option[Int] = Some(value = 12)

({(_: Int) + 3}.some) ap 10.some
// res17: Option[Int] = Some(value = 13)

({(_: String) + "hahah"}.some) ap none[String]
// res18: Option[String] = None

(none[String => String]) ap "woot".some
// res19: Option[String] = None

Useful functions for Apply 

LYAHFGG:

Control.Applicative defines a function that’s called liftA2, which has a type of

liftA2 :: (Applicative f) => (a -> b -> c) -> f a -> f b -> f c .

Remember parameters are flipped around in Scala. What we have is a function that takes F[B] and F[A], then a function (A, B) => C. This is called map2 on Apply.

@typeclass(excludeParents = List("ApplyArityFunctions"))
trait Apply[F[_]] extends Functor[F] with Cartesian[F] with ApplyArityFunctions[F] { self =>
  def ap[A, B](ff: F[A => B])(fa: F[A]): F[B]

  def productR[A, B](fa: F[A])(fb: F[B]): F[B] =
    map2(fa, fb)((_, b) => b)

  def productL[A, B](fa: F[A])(fb: F[B]): F[A] =
    map2(fa, fb)((a, _) => a)

  override def product[A, B](fa: F[A], fb: F[B]): F[(A, B)] =
    ap(map(fa)(a => (b: B) => (a, b)))(fb)

  /** Alias for [[ap]]. */
  @inline final def <*>[A, B](ff: F[A => B])(fa: F[A]): F[B] =
    ap(ff)(fa)

  /** Alias for [[productR]]. */
  @inline final def *>[A, B](fa: F[A])(fb: F[B]): F[B] =
    productR(fa)(fb)

  /** Alias for [[productL]]. */
  @inline final def <*[A, B](fa: F[A])(fb: F[B]): F[A] =
    productL(fa)(fb)

  /**
   * ap2 is a binary version of ap, defined in terms of ap.
   */
  def ap2[A, B, Z](ff: F[(A, B) => Z])(fa: F[A], fb: F[B]): F[Z] =
    map(product(fa, product(fb, ff))) { case (a, (b, f)) => f(a, b) }

  def map2[A, B, Z](fa: F[A], fb: F[B])(f: (A, B) => Z): F[Z] =
    map(product(fa, fb))(f.tupled)

  def map2Eval[A, B, Z](fa: F[A], fb: Eval[F[B]])(f: (A, B) => Z): Eval[F[Z]] =
    fb.map(fb => map2(fa, fb)(f))

  ....
}

For binary operators, map2 can be used to hide the applicative style. Here we can write the same thing in two different ways:

(3.some, List(4).some) mapN { _ :: _ }
// res20: Option[List[Int]] = Some(value = List(3, 4))

Apply[Option].map2(3.some, List(4).some) { _ :: _ }
// res21: Option[List[Int]] = Some(value = List(3, 4))

The results match up.

The 2-parameter version of Apply[F].ap is called Apply[F].ap2:

Apply[Option].ap2({{ (_: Int) :: (_: List[Int]) }.some })(3.some, List(4).some)
// res22: Option[List[Int]] = Some(value = List(3, 4))

There’s a special case of map2 called tuple2, which works like this:

Apply[Option].tuple2(1.some, 2.some)
// res23: Option[(Int, Int)] = Some(value = (1, 2))

Apply[Option].tuple2(1.some, none[Int])
// res24: Option[(Int, Int)] = None

If you are wondering what happens when you have a function with more than two parameters, note that Apply[F[_]] extends ApplyArityFunctions[F]. This is auto-generated code that defines ap3, map3, tuple3, … up to ap22, map22, tuple22.

Apply law 

Apply has a single law called composition:

trait ApplyLaws[F[_]] extends FunctorLaws[F] {
  implicit override def F: Apply[F]

  def applyComposition[A, B, C](fa: F[A], fab: F[A => B], fbc: F[B => C]): IsEq[F[C]] = {
    val compose: (B => C) => (A => B) => (A => C) = _.compose
    fa.ap(fab).ap(fbc) <-> fa.ap(fab.ap(fbc.map(compose)))
  }
}

Applicative 

Note: If you jumped to this page because you’re interested in applicative functors, you should definitely read Semigroupal and Apply first.

Functors, Applicative Functors and Monoids:

Meet the Applicative typeclass. It lies in the Control.Applicative module and it defines two methods, pure and <*>.

Let’s see Cats’ Applicative:

@typeclass trait Applicative[F[_]] extends Apply[F] { self =>
  /**
   * `pure` lifts any value into the Applicative Functor
   *
   * Applicative[Option].pure(10) = Some(10)
   */
  def pure[A](x: A): F[A]

  ....
}

It’s an extension of Apply with pure.

LYAHFGG:

pure should take a value of any type and return an applicative value with that value inside it. … A better way of thinking about pure would be to say that it takes a value and puts it in some sort of default (or pure) context—a minimal context that still yields that value.

It seems like it’s basically a constructor that takes value A and returns F[A].

import cats._, cats.syntax.all._

Applicative[List].pure(1)
// res0: List[Int] = List(1)

Applicative[Option].pure(1)
// res1: Option[Int] = Some(value = 1)

This actually comes in handy using Apply[F].ap so we can avoid calling {{...}.some}.

{
  val F = Applicative[Option]
  F.ap({ F.pure((_: Int) + 3) })(F.pure(9))
}
// res2: Option[Int] = Some(value = 12)

We’ve abstracted Option away from the code.

Useful functions for Applicative 

LYAHFGG:

Let’s try implementing a function that takes a list of applicatives and returns an applicative that has a list as its result value. We’ll call it sequenceA.

sequenceA :: (Applicative f) => [f a] -> f [a]
sequenceA [] = pure []
sequenceA (x:xs) = (:) <$> x <*> sequenceA xs

Let’s try implementing this with Cats!

def sequenceA[F[_]: Applicative, A](list: List[F[A]]): F[List[A]] = list match {
  case Nil     => Applicative[F].pure(Nil: List[A])
  case x :: xs => (x, sequenceA(xs)) mapN {_ :: _}
}

Let’s test it:

sequenceA(List(1.some, 2.some))
// res3: Option[List[Int]] = Some(value = List(1, 2))

sequenceA(List(3.some, none[Int], 1.some))
// res4: Option[List[Int]] = None

sequenceA(List(List(1, 2, 3), List(4, 5, 6)))
// res5: List[List[Int]] = List(
//   List(1, 4),
//   List(1, 5),
//   List(1, 6),
//   List(2, 4),
//   List(2, 5),
//   List(2, 6),
//   List(3, 4),
//   List(3, 5),
//   List(3, 6)
// )

We got the right answers. What’s interesting here is that we did end up needing Applicative after all, and sequenceA is generic in a typeclassy way.

Using sequenceA is useful when we have a list of functions and we want to feed the same input to all of them and then view the list of results.

For Function1 with Int fixed example, we need some type annotation:

{
  val f = sequenceA[Function1[Int, *], Int](List((_: Int) + 3, (_: Int) + 2, (_: Int) + 1))
  f(3)
}
// res6: List[Int] = List(6, 5, 4)

Applicative Laws 

Here are the laws for Applicative:

• identity: pure id <*> v = v
• homomorphism: pure f <*> pure x = pure (f x)
• interchange: u <*> pure y = pure ($ y) <*> u

Cats defines another law

  def applicativeMap[A, B](fa: F[A], f: A => B): IsEq[F[B]] =
    fa.map(f) <-> fa.ap(F.pure(f))

This seem to say that if you combine F.ap and F.pure, you should get the same effect as F.map.

It took us a while, but I am glad we got this far. We’ll pick it up from here later.

day 4 

Yesterday we reviewed kinds and types, explored Apply, applicative style, and ended with sequenceA.

Let’s move on to Semigroup and Monoid today.

Semigroup 

If you have the book Learn You a Haskell for Great Good you get to start a new chapter: “Monoids.” For the website, it’s still Functors, Applicative Functors and Monoids.

First, it seems like Cats is missing newtype/tagged type facility. We’ll implement our own later.

Haskell’s Monoid is split into Semigroup and Monoid in Cats. They are also type aliases of algebra.Semigroup and algebra.Monoid. As with Apply and Applicative, Semigroup is a weaker version of Monoid. If you can solve the same problem, weaker is cooler because you’re making fewer assumptions.

LYAHFGG:

It doesn’t matter if we do (3 * 4) * 5 or 3 * (4 * 5). Either way, the result is 60. The same goes for ++. …

We call this property associativity. * is associative, and so is ++, but -, for example, is not.

Let’s check this:

import cats._, cats.syntax.all._

assert { (3 * 2) * (8 * 5) === 3 * (2 * (8 * 5)) }

assert { List("la") ++ (List("di") ++ List("da")) === (List("la") ++ List("di")) ++ List("da") }

No error means, they are equal.

The Semigroup typeclass 

Here’s the typeclass contract for algebra.Semigroup.

/**
 * A semigroup is any set `A` with an associative operation (`combine`).
 */
trait Semigroup[@sp(Int, Long, Float, Double) A] extends Any with Serializable {

  /**
   * Associative operation taking which combines two values.
   */
  def combine(x: A, y: A): A

  ....
}

This enables combine operator and its symbolic alias |+|. Let’s try using this.

List(1, 2, 3) |+| List(4, 5, 6)
// res2: List[Int] = List(1, 2, 3, 4, 5, 6)

"one" |+| "two"
// res3: String = "onetwo"

The Semigroup Laws 

Associativity is the only law for Semigroup.

• associativity (x |+| y) |+| z = x |+| (y |+| z)

Here’s how we can check the Semigroup laws from the REPL. Review Checking laws with discipline for the details:

scala> import cats._, cats.data._, cats.implicits._
import cats._
import cats.data._
import cats.implicits._

scala> import cats.kernel.laws.GroupLaws
import cats.kernel.laws.GroupLaws

scala> val rs1 = GroupLaws[Int].semigroup(Semigroup[Int])
rs1: cats.kernel.laws.GroupLaws[Int]#GroupProperties = cats.kernel.laws.GroupLaws$GroupProperties@5a077d1d

scala> rs1.all.check
+ semigroup.associativity: OK, passed 100 tests.
+ semigroup.combineN(a, 1) == a: OK, passed 100 tests.
+ semigroup.combineN(a, 2) == a |+| a: OK, passed 100 tests.
+ semigroup.serializable: OK, proved property.

Lists are Semigroups 

List(1, 2, 3) |+| List(4, 5, 6)
// res4: List[Int] = List(1, 2, 3, 4, 5, 6)

Product and Sum 

For Int a semigroup can be formed under both + and *. Instead of tagged types, cats provides only the instance additive.

Trying to use operator syntax here is tricky.

def doSomething[A: Semigroup](a1: A, a2: A): A =
  a1 |+| a2

doSomething(3, 5)(Semigroup[Int])
// res5: Int = 8

I might as well stick to function syntax:

Semigroup[Int].combine(3, 5)
// res6: Int = 8

Monoid 

LYAHFGG:

It seems that both * together with 1 and ++ along with [] share some common properties:

• The function takes two parameters.
• The parameters and the returned value have the same type.
• There exists such a value that doesn’t change other values when used with the binary function.

Let’s check it out in Scala:

4 * 1
// res0: Int = 4

1 * 9
// res1: Int = 9

List(1, 2, 3) ++ Nil
// res2: List[Int] = List(1, 2, 3)

Nil ++ List(0.5, 2.5)
// res3: List[Double] = List(0.5, 2.5)

Looks right.

Monoid typeclass 

Here’s the typeclass contract of algebra.Monoid:

/**
 * A monoid is a semigroup with an identity. A monoid is a specialization of a
 * semigroup, so its operation must be associative. Additionally,
 * `combine(x, empty) == combine(empty, x) == x`. For example, if we have `Monoid[String]`,
 * with `combine` as string concatenation, then `empty = ""`.
 */
trait Monoid[@sp(Int, Long, Float, Double) A] extends Any with Semigroup[A] {

  /**
   * Return the identity element for this monoid.
   */
  def empty: A

  ...
}

Monoid laws 

In addition to the semigroup law, monoid must satify two more laws:

• associativity (x |+| y) |+| z = x |+| (y |+| z)
• left identity Monoid[A].empty |+| x = x
• right identity x |+| Monoid[A].empty = x

Here’s how we can check monoid laws from the REPL:

scala> import cats._, cats.syntax.all._
import cats._
import cats.syntax.all._

scala> import cats.kernel.laws.discipline.MonoidTests
import cats.kernel.laws.discipline.MonoidTests

scala> import org.scalacheck.Test.Parameters
import org.scalacheck.Test.Parameters

scala> val rs1 = MonoidTests[Int].monoid
val rs1: cats.kernel.laws.discipline.MonoidTests[Int]#RuleSet = org.typelevel.discipline.Laws$DefaultRuleSet@108684fb

scala> rs1.all.check(Parameters.default)
+ monoid.associative: OK, passed 100 tests.
+ monoid.collect0: OK, passed 100 tests.
+ monoid.combine all: OK, passed 100 tests.
+ monoid.combineAllOption: OK, passed 100 tests.
+ monoid.intercalateCombineAllOption: OK, passed 100 tests.
+ monoid.intercalateIntercalates: OK, passed 100 tests.
+ monoid.intercalateRepeat1: OK, passed 100 tests.
+ monoid.intercalateRepeat2: OK, passed 100 tests.
+ monoid.is id: OK, passed 100 tests.
+ monoid.left identity: OK, passed 100 tests.
+ monoid.repeat0: OK, passed 100 tests.
+ monoid.repeat1: OK, passed 100 tests.
+ monoid.repeat2: OK, passed 100 tests.
+ monoid.reverseCombineAllOption: OK, passed 100 tests.
+ monoid.reverseRepeat1: OK, passed 100 tests.
+ monoid.reverseRepeat2: OK, passed 100 tests.
+ monoid.reverseReverses: OK, passed 100 tests.
+ monoid.right identity: OK, passed 100 tests.

Here’s the MUnit test of the above:

package example

import cats._
import cats.kernel.laws.discipline.MonoidTests

class IntTest extends munit.DisciplineSuite {
  checkAll("Int", MonoidTests[Int].monoid)
}

Value classes 

LYAHFGG:

The newtype keyword in Haskell is made exactly for these cases when we want to just take one type and wrap it in something to present it as another type.

Cats does not ship with a tagged-type facility, but Scala now has value classes. This will remain unboxed under certain conditions, so it should work for simple examples.

class Wrapper(val unwrap: Int) extends AnyVal

Disjunction and Conjunction 

LYAHFGG:

Another type which can act like a monoid in two distinct but equally valid ways is Bool. The first way is to have the or function || act as the binary function along with False as the identity value. … The other way for Bool to be an instance of Monoid is to kind of do the opposite: have && be the binary function and then make True the identity value.

Cats does not provide this, but we can implement it ourselves.

import cats._, cats.syntax.all._

// `class Disjunction(val unwrap: Boolean) extends AnyVal` doesn't work on mdoc
class Disjunction(val unwrap: Boolean)

object Disjunction {
  @inline def apply(b: Boolean): Disjunction = new Disjunction(b)
  implicit val disjunctionMonoid: Monoid[Disjunction] = new Monoid[Disjunction] {
    def combine(a1: Disjunction, a2: Disjunction): Disjunction =
      Disjunction(a1.unwrap || a2.unwrap)
    def empty: Disjunction = Disjunction(false)
  }
  implicit val disjunctionEq: Eq[Disjunction] = new Eq[Disjunction] {
    def eqv(a1: Disjunction, a2: Disjunction): Boolean =
      a1.unwrap == a2.unwrap
  }
}

val x1 = Disjunction(true) |+| Disjunction(false)
// x1: Disjunction = repl.MdocSessionDisjunction@564bc78f

x1.unwrap
// res4: Boolean = true

val x2 = Monoid[Disjunction].empty |+| Disjunction(true)
// x2: Disjunction = repl.MdocSessionDisjunction@1b6cb4c9

x2.unwrap
// res5: Boolean = true

Here’s conjunction:

// `class Conjunction(val unwrap: Boolean) extends AnyVal` doesn't work on mdoc
class Conjunction(val unwrap: Boolean)

object Conjunction {
  @inline def apply(b: Boolean): Conjunction = new Conjunction(b)
  implicit val conjunctionMonoid: Monoid[Conjunction] = new Monoid[Conjunction] {
    def combine(a1: Conjunction, a2: Conjunction): Conjunction =
      Conjunction(a1.unwrap && a2.unwrap)
    def empty: Conjunction = Conjunction(true)
  }
  implicit val conjunctionEq: Eq[Conjunction] = new Eq[Conjunction] {
    def eqv(a1: Conjunction, a2: Conjunction): Boolean =
      a1.unwrap == a2.unwrap
  }
}

val x3 = Conjunction(true) |+| Conjunction(false)
// x3: Conjunction = repl.MdocSessionConjunction@20ce751

x3.unwrap
// res6: Boolean = false

val x4 = Monoid[Conjunction].empty |+| Conjunction(true)
// x4: Conjunction = repl.MdocSessionConjunction@201bb9f7

x4.unwrap
// res7: Boolean = true

We should check if our custom new types satisfy the the monoid laws.

scala> import cats._, cats.syntax.all._
import cats._
import cats.syntax.all._

scala> import cats.kernel.laws.discipline.MonoidTests
import cats.kernel.laws.discipline.MonoidTests

scala> import org.scalacheck.Test.Parameters
import org.scalacheck.Test.Parameters

scala> import org.scalacheck.{ Arbitrary, Gen }
import org.scalacheck.{Arbitrary, Gen}

scala> implicit def arbDisjunction(implicit ev: Arbitrary[Boolean]): Arbitrary[Disjunction] =
         Arbitrary { ev.arbitrary map { Disjunction(_) } }
def arbDisjunction(implicit ev: org.scalacheck.Arbitrary[Boolean]): org.scalacheck.Arbitrary[Disjunction]

scala> val rs1 = MonoidTests[Disjunction].monoid
val rs1: cats.kernel.laws.discipline.MonoidTests[Disjunction]#RuleSet = org.typelevel.discipline.Laws$DefaultRuleSet@464d134

scala> rs1.all.check(Parameters.default)
+ monoid.associative: OK, passed 100 tests.
+ monoid.collect0: OK, passed 100 tests.
+ monoid.combine all: OK, passed 100 tests.
+ monoid.combineAllOption: OK, passed 100 tests.
....

Disjunction looks ok.

scala> implicit def arbConjunction(implicit ev: Arbitrary[Boolean]): Arbitrary[Conjunction] =
         Arbitrary { ev.arbitrary map { Conjunction(_) } }
def arbConjunction(implicit ev: org.scalacheck.Arbitrary[Boolean]): org.scalacheck.Arbitrary[Conjunction]

scala> val rs2 = MonoidTests[Conjunction].monoid
val rs2: cats.kernel.laws.discipline.MonoidTests[Conjunction]#RuleSet = org.typelevel.discipline.Laws$DefaultRuleSet@71a4f643

scala> rs2.all.check(Parameters.default)
+ monoid.associative: OK, passed 100 tests.
+ monoid.collect0: OK, passed 100 tests.
+ monoid.combine all: OK, passed 100 tests.
+ monoid.combineAllOption: OK, passed 100 tests.
....

Conjunction looks ok too.

Option as Monoids 

LYAHFGG:

One way is to treat Maybe a as a monoid only if its type parameter a is a monoid as well and then implement mappend in such a way that it uses the mappend operation of the values that are wrapped with Just.

Let’s see if this is how Cats does it.

  implicit def optionMonoid[A](implicit ev: Semigroup[A]): Monoid[Option[A]] =
    new Monoid[Option[A]] {
      def empty: Option[A] = None
      def combine(x: Option[A], y: Option[A]): Option[A] =
        x match {
          case None => y
          case Some(xx) => y match {
            case None => x
            case Some(yy) => Some(ev.combine(xx,yy))
          }
        }
    }

If we replace mappend with the equivalent combine, the rest is just pattern matching. Let’s try using it.

none[String] |+| "andy".some
// res8: Option[String] = Some(value = "andy")

1.some |+| none[Int]
// res9: Option[Int] = Some(value = 1)

It works.

LYAHFGG:

But if we don’t know if the contents are monoids, we can’t use mappend between them, so what are we to do? Well, one thing we can do is to just discard the second value and keep the first one. For this, the First a type exists.

Haskell is using newtype to implement First type constructor. Since we can’t prevent allocation for generic value class, we can just make a normal case class.

case class First[A: Eq](val unwrap: Option[A])

object First {
  implicit def firstMonoid[A: Eq]: Monoid[First[A]] = new Monoid[First[A]] {
    def combine(a1: First[A], a2: First[A]): First[A] =
      First((a1.unwrap, a2.unwrap) match {
        case (Some(x), _) => Some(x)
        case (None, y)    => y
      })
    def empty: First[A] = First(None: Option[A])
  }
  implicit def firstEq[A: Eq]: Eq[First[A]] = new Eq[First[A]] {
    def eqv(a1: First[A], a2: First[A]): Boolean =
      Eq[Option[A]].eqv(a1.unwrap, a2.unwrap)
  }
}

First('a'.some) |+| First('b'.some)
// res10: First[Char] = First(unwrap = Some(value = 'a'))

First(none[Char]) |+| First('b'.some)
// res11: First[Char] = First(unwrap = Some(value = 'b'))

Let’s check the laws:

scala> implicit def arbFirst[A: Eq](implicit ev: Arbitrary[Option[A]]): Arbitrary[First[A]] =
         Arbitrary { ev.arbitrary map { First(_) } }
def arbFirst[A](implicit evidence$1: cats.Eq[A], ev: org.scalacheck.Arbitrary[Option[A]]): org.scalacheck.Arbitrary[First[A]]

scala> val rs3 = MonoidTests[First[Int]].monoid
val rs3: cats.kernel.laws.discipline.MonoidTests[First[Int]]#RuleSet = org.typelevel.discipline.Laws$DefaultRuleSet@17d3711d

scala> rs3.all.check(Parameters.default)
+ monoid.associative: OK, passed 100 tests.
+ monoid.collect0: OK, passed 100 tests.
+ monoid.combine all: OK, passed 100 tests.
+ monoid.combineAllOption: OK, passed 100 tests.
....

It thinks First is not serializable either.

LYAHFGG:

If we want a monoid on Maybe a such that the second parameter is kept if both parameters of mappend are Just values, Data.Monoid provides a the Last a type.

case class Last[A: Eq](val unwrap: Option[A])

object Last {
  implicit def lastMonoid[A: Eq]: Monoid[Last[A]] = new Monoid[Last[A]] {
    def combine(a1: Last[A], a2: Last[A]): Last[A] =
      Last((a1.unwrap, a2.unwrap) match {
        case (_, Some(y)) => Some(y)
        case (x, None)    => x
      })
    def empty: Last[A] = Last(None: Option[A])
  }
  implicit def lastEq[A: Eq]: Eq[Last[A]] = new Eq[Last[A]] {
    def eqv(a1: Last[A], a2: Last[A]): Boolean =
      Eq[Option[A]].eqv(a1.unwrap, a2.unwrap)
  }
}

Last('a'.some) |+| Last('b'.some)
// res12: Last[Char] = Last(unwrap = Some(value = 'b'))

Last('a'.some) |+| Last(none[Char])
// res13: Last[Char] = Last(unwrap = Some(value = 'a'))

More law checking:

scala> implicit def arbLast[A: Eq](implicit ev: Arbitrary[Option[A]]): Arbitrary[Last[A]] =
         Arbitrary { ev.arbitrary map { Last(_) } }
def arbLast[A](implicit evidence$1: cats.Eq[A], ev: org.scalacheck.Arbitrary[Option[A]]): org.scalacheck.Arbitrary[Last[A]]

scala> val rs4 = MonoidTests[Last[Int]].monoid
val rs4: cats.kernel.laws.discipline.MonoidTests[Last[Int]]#RuleSet = org.typelevel.discipline.Laws$DefaultRuleSet@7b28ea53

scala> rs4.all.check(Parameters.default)
+ monoid.associative: OK, passed 100 tests.
+ monoid.collect0: OK, passed 100 tests.
+ monoid.combine all: OK, passed 100 tests.
+ monoid.combineAllOption: OK, passed 100 tests.
....

I think we got a pretty good feel for monoids.

About Laws 

We covered lots of things around laws today. Why do we need laws anyway?

Laws are important because laws are important is a tautological statement, but there’s a grain of truth to it. Like traffic laws dictating that we drive on one side within a patch of land, some laws are convenient if everyone follows them.

What Cats/Haskell-style function programming allows us to do is write code that abstracts out the data, container, execution model, etc. The abstraction will make only the assumptions stated in the laws, thus each A: Monoid needs to satisfy the laws for the abstracted code to behave properly. We can call this the utilitarian view.

Even if we could accept the utility, why those laws? It’s because it’s on HaskellWiki or one of SPJ’s papers. They might offer a starting point with an existing implementation, which we can mimic. We can call this the traditionalist view. However, there is a danger of inheriting the design choices or even limitations that were made specifically for Haskell. Functor in category theory, for instance, is a more general term than Functor[F]. At least fmap is a function that returns F[A] => F[B], which is related. By the time we get to map in Scala, we lose that because of type inference.

Eventually we should tie our understanding back to math. Monoid laws correspond with the mathematical definition of monoids, and from there we can reap the benefits of the known properties of monoids. This is relevant especially for monoid laws, because the three laws are the same as the axioms of the category, because a monoid is a special case of a category.

For the sake of learning, I think it’s ok to start out with cargo cult. We all learn language through imitation and pattern recognition.

Using monoids to fold data structures 

LYAHFGG:

Because there are so many data structures that work nicely with folds, the Foldable type class was introduced. Much like Functor is for things that can be mapped over, Foldable is for things that can be folded up!

The equivalent in Cats is also called Foldable. Here’s the typeclass contract:

/**
 * Data structures that can be folded to a summary value.
 *
 * In the case of a collection (such as `List` or `Set`), these
 * methods will fold together (combine) the values contained in the
 * collection to produce a single result. Most collection types have
 * `foldLeft` methods, which will usually be used by the associationed
 * `Fold[_]` instance.
 *
 * Foldable[F] is implemented in terms of two basic methods:
 *
 *  - `foldLeft(fa, b)(f)` eagerly folds `fa` from left-to-right.
 *  - `foldLazy(fa, b)(f)` lazily folds `fa` from right-to-left.
 *
 * Beyond these it provides many other useful methods related to
 * folding over F[A] values.
 *
 * See: [[https://www.cs.nott.ac.uk/~gmh/fold.pdf A tutorial on the universality and expressiveness of fold]]
 */
@typeclass trait Foldable[F[_]] extends Serializable { self =>

  /**
   * Left associative fold on 'F' using the function 'f'.
   */
  def foldLeft[A, B](fa: F[A], b: B)(f: (B, A) => B): B

  /**
   * Right associative lazy fold on `F` using the folding function 'f'.
   *
   * This method evaluates `b` lazily (in some cases it will not be
   * needed), and returns a lazy value. We are using `A => Fold[B]` to
   * support laziness in a stack-safe way.
   *
   * For more detailed information about how this method works see the
   * documentation for `Fold[_]`.
   */
  def foldLazy[A, B](fa: F[A], lb: Lazy[B])(f: A => Fold[B]): Lazy[B] =
    Lazy(partialFold[A, B](fa)(f).complete(lb))

  /**
   * Low-level method that powers `foldLazy`.
   */
  def partialFold[A, B](fa: F[A])(f: A => Fold[B]): Fold[B]
  ....
}

We can use this as follows:

import cats._, cats.syntax.all._

Foldable[List].foldLeft(List(1, 2, 3), 1) {_ * _}
// res0: Int = 6

Foldable comes with some useful functions/operators, many of them taking advantage of the typeclasses. Let’s try the fold. Monoid[A] gives us empty and combine, so that’s enough information to fold over things.

  /**
   * Fold implemented using the given Monoid[A] instance.
   */
  def fold[A](fa: F[A])(implicit A: Monoid[A]): A =
    foldLeft(fa, A.empty) { (acc, a) =>
      A.combine(acc, a)
    }

Let’s try this out.

Foldable[List].fold(List(1, 2, 3))(Monoid[Int])
// res1: Int = 6

There’s a variant called foldMap that accepts a function.

  /**
   * Fold implemented by mapping `A` values into `B` and then
   * combining them using the given `Monoid[B]` instance.
   */
  def foldMap[A, B](fa: F[A])(f: A => B)(implicit B: Monoid[B]): B =
    foldLeft(fa, B.empty) { (b, a) =>
      B.combine(b, f(a))
    }

Since the standard collection library doesn’t implement foldMap, we can now use this as an operator.

List(1, 2, 3).foldMap(identity)(Monoid[Int])
// res2: Int = 6

Another useful thing is that we can use this to convert the values into newtype.

// `class Conjunction(val unwrap: Boolean) extends AnyVal` doesn't work on mdoc
class Conjunction(val unwrap: Boolean)

object Conjunction {
  @inline def apply(b: Boolean): Conjunction = new Conjunction(b)
  implicit val conjunctionMonoid: Monoid[Conjunction] = new Monoid[Conjunction] {
    def combine(a1: Conjunction, a2: Conjunction): Conjunction =
      Conjunction(a1.unwrap && a2.unwrap)
    def empty: Conjunction = Conjunction(true)
  }
  implicit val conjunctionEq: Eq[Conjunction] = new Eq[Conjunction] {
    def eqv(a1: Conjunction, a2: Conjunction): Boolean =
      a1.unwrap == a2.unwrap
  }
}

val x = List(true, false, true) foldMap {Conjunction(_)}
// x: Conjunction = repl.MdocSessionConjunction@6eed0bc2
x.unwrap
// res3: Boolean = false

This surely beats writing Conjunction(true) for each of them and connecting them with |+|.

We will pick it up from here later.

day 5 

Derived from Bello Nock's Sky Walk by Chris Phutully

Yesterday we reviewed Semigroup and Monoid, implementing custom monoids along the way. We also looked at Foldable that can foldMap etc.

Apply.ap 

Starting with a few updates today. First, Apply.apply that we looked at in day 3 has been renamed to Apply.ap #308.

Serializable typeclass instance 

In a previous version, checking the monoid laws on a value class kept tripping on Serializable. That turned out not to be Cats’ fault. I went into Cats’ gitter chat and Erik (@d6/@non) kindly pointed out that the reason my typeclass instances are not serializable is because they are defined on the REPL. Once I moved First to src/ the laws passed fine.

Jason Zaugg (@retronym) also pointed that, to support serialization beyond precisely the same version of Cats on both sides of the wire, we need to do more things like:

• Avoid anonymous classes (to avoid class name change)
• Tack @SerialVersionUID(0L) on everything

FlatMap 

We get to start a new chapter today on Learn You a Haskell for Great Good.

Monads are a natural extension applicative functors, and they provide a solution to the following problem: If we have a value with context, m a, how do we apply it to a function that takes a normal a and returns a value with a context.

Cats breaks down the Monad typeclass into two typeclasses: FlatMap and Monad. Here’s the typeclass contract for FlatMap:

@typeclass trait FlatMap[F[_]] extends Apply[F] {
  def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B]

  def tailRecM[A, B](a: A)(f: A => F[Either[A, B]]): F[B]

  ....
}

Note that FlatMap extends Apply, the weaker version of Applicative. And here are the operators:

class FlatMapOps[F[_], A](fa: F[A])(implicit F: FlatMap[F]) {
  def flatMap[B](f: A => F[B]): F[B] = F.flatMap(fa)(f)
  def mproduct[B](f: A => F[B]): F[(A, B)] = F.mproduct(fa)(f)
  def >>=[B](f: A => F[B]): F[B] = F.flatMap(fa)(f)
  def >>[B](fb: F[B]): F[B] = F.flatMap(fa)(_ => fb)
}

It introduces the flatMap operator and its symbolic alias >>=. We’ll worry about the other operators later. We are used to flapMap from the standard library:

import cats._, cats.syntax.all._

(Right(3): Either[String, Int]) flatMap { x => Right(x + 1) }
// res0: Either[String, Int] = Right(value = 4)

Getting our feet wet with Option 

Following the book, let’s explore Option. In this section I’ll be less fussy about whether it’s using Cats’ typeclass or standard library’s implementation. Here’s Option as a functor:

"wisdom".some map { _ + "!" }
// res1: Option[String] = Some(value = "wisdom!")

none[String] map { _ + "!" }
// res2: Option[String] = None

Here’s Option as an Apply:

({(_: Int) + 3}.some) ap 3.some
// res3: Option[Int] = Some(value = 6)

none[String => String] ap "greed".some
// res4: Option[String] = None

({(_: String).toInt}.some) ap none[String]
// res5: Option[Int] = None

Here’s Option as a FlatMap:

3.some flatMap { (x: Int) => (x + 1).some }
// res6: Option[Int] = Some(value = 4)

"smile".some flatMap { (x: String) =>  (x + " :)").some }
// res7: Option[String] = Some(value = "smile :)")

none[Int] flatMap { (x: Int) => (x + 1).some }
// res8: Option[Int] = None

none[String] flatMap { (x: String) =>  (x + " :)").some }
// res9: Option[String] = None

Just as expected, we get None if the monadic value is None.

FlatMap laws 

FlatMap has a single law called associativity:

• associativity: (m flatMap f) flatMap g === m flatMap { x => f(x) flatMap {g} }

Cats defines two more laws in FlatMapLaws:

trait FlatMapLaws[F[_]] extends ApplyLaws[F] {
  implicit override def F: FlatMap[F]

  def flatMapAssociativity[A, B, C](fa: F[A], f: A => F[B], g: B => F[C]): IsEq[F[C]] =
    fa.flatMap(f).flatMap(g) <-> fa.flatMap(a => f(a).flatMap(g))

  def flatMapConsistentApply[A, B](fa: F[A], fab: F[A => B]): IsEq[F[B]] =
    fab.ap(fa) <-> fab.flatMap(f => fa.map(f))

  /**
   * The composition of `cats.data.Kleisli` arrows is associative. This is
   * analogous to [[flatMapAssociativity]].
   */
  def kleisliAssociativity[A, B, C, D](f: A => F[B], g: B => F[C], h: C => F[D], a: A): IsEq[F[D]] = {
    val (kf, kg, kh) = (Kleisli(f), Kleisli(g), Kleisli(h))
    ((kf andThen kg) andThen kh).run(a) <-> (kf andThen (kg andThen kh)).run(a)
  }
}

Monad 

Earlier I wrote that Cats breaks down the Monad typeclass into two typeclasses: FlatMap and Monad. The FlatMap-Monad relationship forms a parallel with the Apply-Applicative relationship:

@typeclass trait Monad[F[_]] extends FlatMap[F] with Applicative[F] {
  ....
}

Monad is a FlatMap with pure. Unlike Haskell, Monad[F] extends Applicative[F] so there’s no return vs pure discrepancies.

Walk the line 

Derived from Bello Nock's Sky Walk by Chris Phutully

LYAHFGG:

Let’s say that [Pierre] keeps his balance if the number of birds on the left side of the pole and on the right side of the pole is within three. So if there’s one bird on the right side and four birds on the left side, he’s okay. But if a fifth bird lands on the left side, then he loses his balance and takes a dive.

Now let’s try implementing the Pole example from the book.

import cats._, cats.syntax.all._

type Birds = Int

case class Pole(left: Birds, right: Birds)

I don’t think it’s common to alias Int like this in Scala, but we’ll go with the flow. I am going to turn Pole into a case class so I can implement landLeft and landRight as methods:

case class Pole(left: Birds, right: Birds) {
  def landLeft(n: Birds): Pole = copy(left = left + n)
  def landRight(n: Birds): Pole = copy(right = right + n)
}

I think it looks better with some OO:

Pole(0, 0).landLeft(2)
// res1: Pole = Pole(left = 2, right = 0)

Pole(1, 2).landRight(1)
// res2: Pole = Pole(left = 1, right = 3)

Pole(1, 2).landRight(-1)
// res3: Pole = Pole(left = 1, right = 1)

We can chain these too:

Pole(0, 0).landLeft(1).landRight(1).landLeft(2)
// res4: Pole = Pole(left = 3, right = 1)

Pole(0, 0).landLeft(1).landRight(4).landLeft(-1).landRight(-2)
// res5: Pole = Pole(left = 0, right = 2)

As the book says, an intermediate value has failed but the calculation kept going. Now let’s introduce failures as Option[Pole]:

case class Pole(left: Birds, right: Birds) {
  def landLeft(n: Birds): Option[Pole] =
    if (math.abs((left + n) - right) < 4) copy(left = left + n).some
    else none[Pole]
  def landRight(n: Birds): Option[Pole] =
    if (math.abs(left - (right + n)) < 4) copy(right = right + n).some
    else none[Pole]
}

Pole(0, 0).landLeft(2)
// res7: Option[Pole] = Some(value = Pole(left = 2, right = 0))

Pole(0, 3).landLeft(10)
// res8: Option[Pole] = None

Now we can chain the landLeft/landRight using flatMap or its symbolic alias >>=.

val rlr = Monad[Option].pure(Pole(0, 0)) >>= {_.landRight(2)} >>=
  {_.landLeft(2)} >>= {_.landRight(2)}
// rlr: Option[Pole] = Some(value = Pole(left = 2, right = 4))

Let’s see if monadic chaining simulates the pole balancing better:

val lrlr = Monad[Option].pure(Pole(0, 0)) >>= {_.landLeft(1)} >>=
  {_.landRight(4)} >>= {_.landLeft(-1)} >>= {_.landRight(-2)}
// lrlr: Option[Pole] = None

It works. Take time to understand this example because this example highlights what a monad is.

1. First, pure puts Pole(0, 0) into a default context: Pole(0, 0).some.
2. Then, Pole(0, 0).some >>= {_.landLeft(1)} happens. Since it’s a Some value, _.landLeft(1) gets applied to Pole(0, 0), resulting to Pole(1, 0).some.
3. Next, Pole(1, 0).some >>= {_.landRight(4)} takes place. The result is Pole(1, 4).some. Now we at at the max difference between left and right.
4. Pole(1, 4).some >>= {_.landLeft(-1)} happens, resulting to none[Pole]. The difference is too great, and pole becomes off balance.
5. none[Pole] >>= {_.landRight(-2)} results automatically to none[Pole].

In this chain of monadic functions, the effect from one function is carried over to the next.

Banana on wire 

LYAHFGG:

We may also devise a function that ignores the current number of birds on the balancing pole and just makes Pierre slip and fall. We can call it banana.

Here’s the banana that always fails:

case class Pole(left: Birds, right: Birds) {
  def landLeft(n: Birds): Option[Pole] =
    if (math.abs((left + n) - right) < 4) copy(left = left + n).some
    else none[Pole]
  def landRight(n: Birds): Option[Pole] =
    if (math.abs(left - (right + n)) < 4) copy(right = right + n).some
    else none[Pole]
  def banana: Option[Pole] = none[Pole]
}

val lbl = Monad[Option].pure(Pole(0, 0)) >>= {_.landLeft(1)} >>=
  {_.banana} >>= {_.landRight(1)}
// lbl: Option[Pole] = None

LYAHFGG:

Instead of making functions that ignore their input and just return a predetermined monadic value, we can use the >> function.

Here’s how >> behaves with Option:

none[Int] >> 3.some
// res10: Option[Int] = None

3.some >> 4.some
// res11: Option[Int] = Some(value = 4)

3.some >> none[Int]
// res12: Option[Int] = None

Let’s try replacing banana with >> none[Pole]:

{
  val lbl = Monad[Option].pure(Pole(0, 0)) >>= {_.landLeft(1)} >>
    none[Pole] >>= {_.landRight(1)}
}
// error: Option[Int] does not take parameters
// 3.some >> none[Int]
//           ^

The type inference broke down all the sudden. The problem is likely the operator precedence. Programming in Scala says:

The one exception to the precedence rule, alluded to above, concerns assignment operators, which end in an equals character. If an operator ends in an equals character (=), and the operator is not one of the comparison operators <=, >=, ==, or !=, then the precedence of the operator is the same as that of simple assignment (=). That is, it is lower than the precedence of any other operator.

Note: The above description is incomplete. Another exception from the assignment operator rule is if it starts with (=) like ===.

Because >>= (bind) ends in the equals character, its precedence is the lowest, which forces ({_.landLeft(1)} >> (none: Option[Pole])) to evaluate first. There are a few unpalatable work arounds. First we can use dot-and-parens like normal method calls:

Monad[Option].pure(Pole(0, 0)).>>=({_.landLeft(1)}).>>(none[Pole]).>>=({_.landRight(1)})
// res14: Option[Pole] = None

Or we can recognize the precedence issue and place parens around just the right place:

(Monad[Option].pure(Pole(0, 0)) >>= {_.landLeft(1)}) >> none[Pole] >>= {_.landRight(1)}
// res15: Option[Pole] = None

Both yield the right result.

for comprehension 

LYAHFGG:

Monads in Haskell are so useful that they got their own special syntax called do notation.

First, let’s write the nested lambda:

3.some >>= { x => "!".some >>= { y => (x.show + y).some } }
// res16: Option[String] = Some(value = "3!")

By using >>=, any part of the calculation can fail:

3.some >>= { x => none[String] >>= { y => (x.show + y).some } }
// res17: Option[String] = None

(none: Option[Int]) >>= { x => "!".some >>= { y => (x.show + y).some } }
// res18: Option[String] = None

3.some >>= { x => "!".some >>= { y => none[String] } }
// res19: Option[String] = None

Instead of the do notation in Haskell, Scala has the for comprehension, which does similar things:

for {
  x <- 3.some
  y <- "!".some
} yield (x.show + y)
// res20: Option[String] = Some(value = "3!")

LYAHFGG:

In a do expression, every line that isn’t a let line is a monadic value.

That’s not quite accurate for for, but we can come back to this later.

Pierre returns 

LYAHFGG:

Our tightwalker’s routine can also be expressed with do notation.

def routine: Option[Pole] =
  for {
    start <- Monad[Option].pure(Pole(0, 0))
    first <- start.landLeft(2)
    second <- first.landRight(2)
    third <- second.landLeft(1)
  } yield third

routine
// res21: Option[Pole] = Some(value = Pole(left = 3, right = 2))

We had to extract third since yield expects Pole not Option[Pole].

LYAHFGG:

If we want to throw the Pierre a banana peel in do notation, we can do the following:

{
  def routine: Option[Pole] =
    for {
      start <- Monad[Option].pure(Pole(0, 0))
      first <- start.landLeft(2)
      _ <- none[Pole]
      second <- first.landRight(2)
      third <- second.landLeft(1)
    } yield third

  routine
}
// res22: Option[Pole] = None

Pattern matching and failure 

LYAHFGG:

In do notation, when we bind monadic values to names, we can utilize pattern matching, just like in let expressions and function parameters.

def justH: Option[Char] =
  for {
    (x :: xs) <- "hello".toList.some
  } yield x

justH
// res23: Option[Char] = Some(value = 'h')

When pattern matching fails in a do expression, the fail function is called. It’s part of the Monad type class and it enables failed pattern matching to result in a failure in the context of the current monad instead of making our program crash.

def wopwop: Option[Char] =
  for {
    (x :: xs) <- "".toList.some
  } yield x

wopwop
// res24: Option[Char] = None

The failed pattern matching returns None here. This is an interesting aspect of for syntax that I haven’t thought about, but totally makes sense.

Monad laws 

Monad had three laws:

• left identity: (Monad[F].pure(x) flatMap {f}) === f(x)
• right identity: (m flatMap {Monad[F].pure(_)}) === m
• associativity: (m flatMap f) flatMap g === m flatMap { x => f(x) flatMap {g} }

LYAHFGG:

The first monad law states that if we take a value, put it in a default context with return and then feed it to a function by using >>=, it’s the same as just taking the value and applying the function to it.

assert { (Monad[Option].pure(3) >>= { x => (x + 100000).some }) ===
  ({ (x: Int) => (x + 100000).some })(3) }

LYAHFGG:

The second law states that if we have a monadic value and we use >>= to feed it to return, the result is our original monadic value.

assert { ("move on up".some >>= {Monad[Option].pure(_)}) === "move on up".some }

LYAHFGG:

The final monad law says that when we have a chain of monadic function applications with >>=, it shouldn’t matter how they’re nested.

Monad[Option].pure(Pole(0, 0)) >>= {_.landRight(2)} >>= {_.landLeft(2)} >>= {_.landRight(2)}
// res27: Option[Pole] = Some(value = Pole(left = 2, right = 4))

Monad[Option].pure(Pole(0, 0)) >>= { x =>
  x.landRight(2) >>= { y =>
  y.landLeft(2) >>= { z =>
  z.landRight(2)
}}}
// res28: Option[Pole] = Some(value = Pole(left = 2, right = 4))

These laws look might look familiar if you remember monoid laws from day 4. That’s because monad is a special kind of a monoid.

You might be thinking, “But wait. Isn’t Monoid for kind A (or *)?” Yes, you’re right. And that’s the difference between monoid with lowercase m and Monoid[A]. Haskell-style functional programming allows you to abstract out the container and execution model. In category theory, a notion like monoid can be generalized to A, F[A], F[A] => F[B] and all sorts of things. Instead of thinking “omg so many laws,” know that there’s an underlying structure that connects many of them.

Here’s how to check Monad laws using Discipline:

scala> import cats._, cats.syntax.all._, cats.laws.discipline.MonadTests
import cats._
import cats.syntax.all._
import cats.laws.discipline.MonadTests

scala> val rs = MonadTests[Option].monad[Int, Int, Int]
val rs: cats.laws.discipline.MonadTests[Option]#RuleSet = cats.laws.discipline.MonadTests$$anon$1@253d7b2b

scala> import org.scalacheck.Test.Parameters
import org.scalacheck.Test.Parameters

scala> rs.all.check(Parameters.default)
+ monad.ap consistent with product + map: OK, passed 100 tests.
+ monad.applicative homomorphism: OK, passed 100 tests.
+ monad.applicative identity: OK, passed 100 tests.
+ monad.applicative interchange: OK, passed 100 tests.
+ monad.applicative map: OK, passed 100 tests.
+ monad.applicative unit: OK, passed 100 tests.
+ monad.apply composition: OK, passed 100 tests.
+ monad.covariant composition: OK, passed 100 tests.
+ monad.covariant identity: OK, passed 100 tests.
+ monad.flatMap associativity: OK, passed 100 tests.
+ monad.flatMap consistent apply: OK, passed 100 tests.
+ monad.flatMap from tailRecM consistency: OK, passed 100 tests.
+ monad.invariant composition: OK, passed 100 tests.
+ monad.invariant identity: OK, passed 100 tests.
+ monad.map flatMap coherence: OK, passed 100 tests.
+ monad.map2/map2Eval consistency: OK, passed 100 tests.
+ monad.map2/product-map consistency: OK, passed 100 tests.
+ monad.monad left identity: OK, passed 100 tests.
+ monad.monad right identity: OK, passed 100 tests.
+ monad.monoidal left identity: OK, passed 100 tests.
+ monad.monoidal right identity: OK, passed 100 tests.
+ monad.mproduct consistent flatMap: OK, passed 100 tests.
+ monad.productL consistent map2: OK, passed 100 tests.
+ monad.productR consistent map2: OK, passed 100 tests.
+ monad.semigroupal associativity: OK, passed 100 tests.
+ monad.tailRecM consistent flatMap: OK, passed 100 tests.
+ monad.tailRecM stack safety: OK, proved property.

List datatype 

LYAHFGG:

On the other hand, a value like [3,8,9] contains several results, so we can view it as one value that is actually many values at the same time. Using lists as applicative functors showcases this non-determinism nicely.

Let’s look at using List as Applicatives again:

import cats._, cats.syntax.all._

(List(1, 2, 3), List(10, 100, 100)) mapN { _ * _ }
// res0: List[Int] = List(10, 100, 100, 20, 200, 200, 30, 300, 300)

let’s try feeding a non-deterministic value to a function:

List(3, 4, 5) >>= { x => List(x, -x) }
// res1: List[Int] = List(3, -3, 4, -4, 5, -5)

So in this monadic view, a List context represents a mathematical value that could have multiple solutions. Other than that manipulating Lists using for notation is just like plain Scala:

for {
  n <- List(1, 2)
  ch <- List('a', 'b')
} yield (n, ch)
// res2: List[(Int, Char)] = List((1, 'a'), (1, 'b'), (2, 'a'), (2, 'b'))

FunctorFilter 

Scala’s for comprehension allows filtering:

// plain Scala

for {
  x <- (1 to 50).toList if x.toString contains '7'
} yield x
// res0: List[Int] = List(7, 17, 27, 37, 47)

Here’s the typeclass contract for `FunctorFilter`:

@typeclass
trait FunctorFilter[F[_]] extends Serializable {
  def functor: Functor[F]

  def mapFilter[A, B](fa: F[A])(f: A => Option[B]): F[B]

  def collect[A, B](fa: F[A])(f: PartialFunction[A, B]): F[B] =
    mapFilter(fa)(f.lift)

  def flattenOption[A](fa: F[Option[A]]): F[A] =
    mapFilter(fa)(identity)

  def filter[A](fa: F[A])(f: A => Boolean): F[A] =
    mapFilter(fa)(a => if (f(a)) Some(a) else None)

  def filterNot[A](fa: F[A])(f: A => Boolean): F[A] =
    mapFilter(fa)(Some(_).filterNot(f))
}

We can use this like this:

import cats._, cats.syntax.all._

val english = Map(1 -> "one", 3 -> "three", 10 -> "ten")
// english: Map[Int, String] = Map(1 -> "one", 3 -> "three", 10 -> "ten")

(1 to 50).toList mapFilter { english.get(_) }
// res1: List[String] = List("one", "three", "ten")

def collectEnglish[F[_]: FunctorFilter](f: F[Int]): F[String] =
  f collect {
    case 1  => "one"
    case 3  => "three"
    case 10 => "ten"
  }

collectEnglish((1 to 50).toList)
// res2: List[String] = List("one", "three", "ten")

def filterSeven[F[_]: FunctorFilter](f: F[Int]): F[Int] =
  f filter { _.show contains '7' }

filterSeven((1 to 50).toList)
// res3: List[Int] = List(7, 17, 27, 37, 47)

A knight’s quest 

LYAHFGG:

Here’s a problem that really lends itself to being solved with non-determinism. Say you have a chess board and only one knight piece on it. We want to find out if the knight can reach a certain position in three moves.

Instead of type aliasing a pair, let’s make this into a case class again:

case class KnightPos(c: Int, r: Int)

Here’s the function to calculate all of the knight’s next positions:

case class KnightPos(c: Int, r: Int) {
  def move: List[KnightPos] =
    for {
      KnightPos(c2, r2) <- List(KnightPos(c + 2, r - 1), KnightPos(c + 2, r + 1),
        KnightPos(c - 2, r - 1), KnightPos(c - 2, r + 1),
        KnightPos(c + 1, r - 2), KnightPos(c + 1, r + 2),
        KnightPos(c - 1, r - 2), KnightPos(c - 1, r + 2)) if (
        ((1 to 8).toList contains c2) && ((1 to 8).toList contains r2))
    } yield KnightPos(c2, r2)
}

KnightPos(6, 2).move
// res1: List[KnightPos] = List(
//   KnightPos(c = 8, r = 1),
//   KnightPos(c = 8, r = 3),
//   KnightPos(c = 4, r = 1),
//   KnightPos(c = 4, r = 3),
//   KnightPos(c = 7, r = 4),
//   KnightPos(c = 5, r = 4)
// )

KnightPos(8, 1).move
// res2: List[KnightPos] = List(
//   KnightPos(c = 6, r = 2),
//   KnightPos(c = 7, r = 3)
// )

The answers look good. Now we implement chaining this three times:

case class KnightPos(c: Int, r: Int) {
  def move: List[KnightPos] =
    for {
      KnightPos(c2, r2) <- List(KnightPos(c + 2, r - 1), KnightPos(c + 2, r + 1),
      KnightPos(c - 2, r - 1), KnightPos(c - 2, r + 1),
      KnightPos(c + 1, r - 2), KnightPos(c + 1, r + 2),
      KnightPos(c - 1, r - 2), KnightPos(c - 1, r + 2)) if (
      ((1 to 8).toList contains c2) && ((1 to 8).toList contains r2))
    } yield KnightPos(c2, r2)
  def in3: List[KnightPos] =
    for {
      first <- move
      second <- first.move
      third <- second.move
    } yield third
  def canReachIn3(end: KnightPos): Boolean = in3 contains end
}

KnightPos(6, 2) canReachIn3 KnightPos(6, 1)
// res4: Boolean = true

KnightPos(6, 2) canReachIn3 KnightPos(7, 3)
// res5: Boolean = false

As it turns out, from (6, 2) you can reach (6, 1) in three moves, but not (7, 3). As with Pierre’s bird example, one of key aspect of the monadic calculation is that the effect of one move can be passed on to the next.

We’ll pick up from here.

day 6 

Yesterday we looked at FlatMap and Monad typeclass. We looked at how monadic chaining can add contexts to values. Because both Option and List already have flatMap in the standard library, it was more about changing the way we see things rather than introducing new code. We also reviewed for syntax as a way of chaining monadic operations.

Before I jump into the topic, I want to mention Pamflet, the Scala-based blog/book platform I’m using here. Nathan Hamblen (@n8han) started Pamflet and I’ve been contributing features to it too. Speaking of which, the source of these posts are also available on eed3si9n/herding-cats if you’re curious how this is built. A special thanks to Leif Wickland (@leifwickland) for proofreading all of the posts and sending me pull requests with fixes!

do vs for 

There are subtle differences in Haskell’s do notation and Scala’s for syntax. Here’s an example of do notation:

foo = do
  x <- Just 3
  y <- Just "!"
  Just (show x ++ y)

Typically one would write return (show x ++ y), but I wrote out Just, so it’s clear that the last line is a monadic value. On the other hand, Scala would look as follows:

def foo = for {
  x <- Some(3)
  y <- Some("!")
} yield x.toString + y

Looks similar, but there are some differences.

• Scala doesn’t have a built-in Monad type. Instead, the compiler desugars for comprehensions into map, withFilter, flatMap, and foreach calls mechanically. SLS 6.19
• For things like Option and List that the standard library implements map/flatMap, the built-in implementations would be prioritized over the typeclasses provided by Cats.
• The Scala collection library’s map etc accepts CanBuildFrom, which may convert F[A] into G[B]. See The Architecture of Scala Collections
• CanBuildFrom may convert some G[A] into F[B].
• yield with a pure value is required, otherwise for turns into Unit.

Here are some demonstration of these points:

import collection.immutable.BitSet

val bits = BitSet(1, 2, 3)
// bits: BitSet = BitSet(1, 2, 3)

for {
  x <- bits
} yield x.toFloat
// res0: collection.immutable.SortedSet[Float] = TreeSet(1.0F, 2.0F, 3.0F)

for {
  i <- List(1, 2, 3)
  j <- Some(1)
} yield i + j
// res1: List[Int] = List(2, 3, 4)

for {
  i <- Map(1 -> 2)
  j <- Some(3)
} yield j
// res2: collection.immutable.Iterable[Int] = List(3)

Implementing actM 

There are several DSLs around in Scala that transforms imperative-looking code into monadic or applicative function calls using macros:

• Scala Async
• Effectful
• sbt 0.13 syntax

Covering full array of Scala syntax in the macro is hard work, but by copy-pasting code from Async and Effectful I put together a toy macro that supports only simple expressions and vals. I’ll omit the details, but the key function is this:

  def transform(group: BindGroup, isPure: Boolean): Tree =
    group match {
      case (binds, tree) =>
        binds match {
          case Nil =>
            if (isPure) q"""$monadInstance.pure($tree)"""
            else tree
          case (name, unwrappedFrom) :: xs =>
            val innerTree = transform((xs, tree), isPure)
            val param = ValDef(Modifiers(Flag.PARAM), name, TypeTree(), EmptyTree)
            q"""$monadInstance.flatMap($unwrappedFrom) { $param => $innerTree }"""
        }
    }

Here’s how we can use actM:

import cats._, cats.syntax.all._
import example.MonadSyntax._

actM[Option, String] {
  val x = 3.some.next
  val y = "!".some.next
  x.toString + y
}
// res3: Option[String] = Some(value = "3!")

fa.next expands to a Monad[F].flatMap(fa)() call. So the above code expands into:

Monad[Option].flatMap[String, String]({
  val fa0: Option[Int] = 3.some
  Monad[Option].flatMap[Int, String](fa0) { (arg0: Int) => {
    val next0: Int = arg0
    val x: Int = next0
    val fa1: Option[String] = "!".some
    Monad[Option].flatMap[String, String](fa1)((arg1: String) => {
      val next1: String = arg1
      val y: String = next1
      Monad[Option].pure[String](x.toString + y)
    })
  }}
}) { (arg2: String) => Monad[Option].pure[String](arg2) }
// res4: Option[String] = Some(value = "3!")

Let’s see if this can prevent auto conversion from Option to List.

{
  actM[List, Int] {
    val i = List(1, 2, 3).next
    val j = 1.some.next
    i + j
  }
}
// error: Option[String] does not take parameters
// Monad[Option].flatMap[String, String]({
// ^

The error message is a bit rough, but we were able to catch this at compile-time. This will also work for any monads including Future.

val x = {
  import scala.concurrent.{ExecutionContext, Future}
  import ExecutionContext.Implicits.global
  actM[Future, Int] {
    val i = Future { 1 }.next
    val j = Future { 2 }.next
    i + j
  }
}
// x: concurrent.Future[Int] = Future(Success(3))

x.value
// res6: Option[util.Try[Int]] = None

This macro is incomplete toy code, but it demonstrates potential usefulness for having something like this.

Writer datatype 

Learn You a Haskell for Great Good says:

Whereas the Maybe monad is for values with an added context of failure, and the list monad is for nondeterministic values, Writer monad is for values that have another value attached that acts as a sort of log value.

Let’s follow the book and implement applyLog function:

def isBigGang(x: Int): (Boolean, String) =
  (x > 9, "Compared gang size to 9.")

implicit class PairOps[A](pair: (A, String)) {
  def applyLog[B](f: A => (B, String)): (B, String) = {
    val (x, log) = pair
    val (y, newlog) = f(x)
    (y, log ++ newlog)
  }
}

(3, "Smallish gang.") applyLog isBigGang
// res0: (Boolean, String) = (false, "Smallish gang.Compared gang size to 9.")

Since method injection is a common use case for implicits, Scala 2.10 adds a syntax sugar called implicit class to make the promotion from a class to an enriched class easier. Here’s how we can generalize the log to a Semigroup:

import cats._, cats.syntax.all._

implicit class PairOps[A, B: Semigroup](pair: (A, B)) {
  def applyLog[C](f: A => (C, B)): (C, B) = {
    val (x, log) = pair
    val (y, newlog) = f(x)
    (y, log |+| newlog)
  }
}

Writer 

LYAHFGG:

To attach a monoid to a value, we just need to put them together in a tuple. The Writer w a type is just a newtype wrapper for this.

In Cats, the equivalent is called `Writer`:

type Writer[L, V] = WriterT[Id, L, V]
object Writer {
  def apply[L, V](l: L, v: V): WriterT[Id, L, V] = WriterT[Id, L, V]((l, v))

  def value[L:Monoid, V](v: V): Writer[L, V] = WriterT.value(v)

  def tell[L](l: L): Writer[L, Unit] = WriterT.tell(l)
}

Writer[L, V] is a type alias for WriterT[Id, L, V]

WriterT 

Here’s the simplified version of `WriterT`:

final case class WriterT[F[_], L, V](run: F[(L, V)]) {
  def tell(l: L)(implicit functorF: Functor[F], semigroupL: Semigroup[L]): WriterT[F, L, V] =
    mapWritten(_ |+| l)

  def written(implicit functorF: Functor[F]): F[L] =
    functorF.map(run)(_._1)

  def value(implicit functorF: Functor[F]): F[V] =
    functorF.map(run)(_._2)

  def mapBoth[M, U](f: (L, V) => (M, U))(implicit functorF: Functor[F]): WriterT[F, M, U] =
    WriterT { functorF.map(run)(f.tupled) }

  def mapWritten[M](f: L => M)(implicit functorF: Functor[F]): WriterT[F, M, V] =
    mapBoth((l, v) => (f(l), v))
}

Here’s how we can create Writer values:

import cats._, cats.data._, cats.syntax.all._

val w = Writer("Smallish gang.", 3)
// w: WriterT[Id, String, Int] = WriterT(run = ("Smallish gang.", 3))

val v = Writer.value[String, Int](3)
// v: Writer[String, Int] = WriterT(run = ("", 3))

val l = Writer.tell[String]("Log something")
// l: Writer[String, Unit] = WriterT(run = ("Log something", ()))

To run the Writer datatype you can call its run method:

w.run
// res2: (String, Int) = ("Smallish gang.", 3)

Using for syntax with Writer 

LYAHFGG:

Now that we have a Monad instance, we’re free to use do notation for Writer values.

def logNumber(x: Int): Writer[List[String], Int] =
  Writer(List("Got number: " + x.show), 3)

def multWithLog: Writer[List[String], Int] =
  for {
    a <- logNumber(3)
    b <- logNumber(5)
  } yield a * b

multWithLog.run
// res3: (List[String], Int) = (List("Got number: 3", "Got number: 5"), 9)

Adding logging to program 

Here’s the gcd example:

def gcd(a: Int, b: Int): Writer[List[String], Int] = {
  if (b == 0) for {
      _ <- Writer.tell(List("Finished with " + a.show))
    } yield a
  else
    Writer.tell(List(s"${a.show} mod ${b.show} = ${(a % b).show}")) >>= { _ =>
      gcd(b, a % b)
    }
}

gcd(12, 16).run
// res4: (List[String], Int) = (
//   List("12 mod 16 = 12", "16 mod 12 = 4", "12 mod 4 = 0", "Finished with 4"),
//   4
// )

Inefficient List construction 

LYAHFGG:

When using the Writer monad, you have to be careful which monoid to use, because using lists can sometimes turn out to be very slow. That’s because lists use ++ for mappend and using ++ to add something to the end of a list is slow if that list is really long.

Here’s the table of performance characteristics for major collections. What stands out for immutable collection is Vector since it has effective constant for all operations. Vector is a tree structure with the branching factor of 32, and it’s able to achieve fast updates by structure sharing.

Here’s the Vector version of gcd:

def gcd(a: Int, b: Int): Writer[Vector[String], Int] = {
  if (b == 0) for {
      _ <- Writer.tell(Vector("Finished with " + a.show))
    } yield a
  else
    Writer.tell(Vector(s"${a.show} mod ${b.show} = ${(a % b).show}")) >>= { _ =>
      gcd(b, a % b)
    }
}

gcd(12, 16).run
// res6: (Vector[String], Int) = (
//   Vector("12 mod 16 = 12", "16 mod 12 = 4", "12 mod 4 = 0", "Finished with 4"),
//   4
// )

Comparing performance 

Like the book let’s write a microbenchmark to compare the performance:

def vectorFinalCountDown(x: Int): Writer[Vector[String], Unit] = {
  import annotation.tailrec
  @tailrec def doFinalCountDown(x: Int, w: Writer[Vector[String], Unit]): Writer[Vector[String], Unit] = x match {
    case 0 => w >>= { _ => Writer.tell(Vector("0")) }
    case x => doFinalCountDown(x - 1, w >>= { _ =>
      Writer.tell(Vector(x.show))
    })
  }
  val t0 = System.currentTimeMillis
  val r = doFinalCountDown(x, Writer.tell(Vector[String]()))
  val t1 = System.currentTimeMillis
  r >>= { _ => Writer.tell(Vector((t1 - t0).show + " msec")) }
}

def listFinalCountDown(x: Int): Writer[List[String], Unit] = {
  import annotation.tailrec
  @tailrec def doFinalCountDown(x: Int, w: Writer[List[String], Unit]): Writer[List[String], Unit] = x match {
    case 0 => w >>= { _ => Writer.tell(List("0")) }
    case x => doFinalCountDown(x - 1, w >>= { _ =>
      Writer.tell(List(x.show))
    })
  }
  val t0 = System.currentTimeMillis
  val r = doFinalCountDown(x, Writer.tell(List[String]()))
  val t1 = System.currentTimeMillis
  r >>= { _ => Writer.tell(List((t1 - t0).show + " msec")) }
}

Here’s the result I got on my machine:

scala> vectorFinalCountDown(10000).run._1.last
res17: String = 6 msec

scala> listFinalCountDown(10000).run._1.last
res18: String = 630 msec

As you can see, List is 100 times slower.

Reader datatype 

Learn You a Haskell for Great Good says:

In the chapter about applicatives, we saw that the function type, (->) r is an instance of Functor.

import cats._, cats.syntax.all._

val f = (_: Int) * 2
// f: Int => Int = <function1>

val g = (_: Int) + 10
// g: Int => Int = <function1>

(g map f)(8)
// res0: Int = 36

We’ve also seen that functions are applicative functors. They allow us to operate on the eventual results of functions as if we already had their results.

{
  val h = (f, g) mapN {_ + _}

  h(3)
}
// res1: Int = 19

Not only is the function type (->) r a functor and an applicative functor, but it’s also a monad. Just like other monadic values that we’ve met so far, a function can also be considered a value with a context. The context for functions is that that value is not present yet and that we have to apply that function to something in order to get its result value.

Let’s try implementing the example:

{
  val addStuff: Int => Int = for {
    a <- (_: Int) * 2
    b <- (_: Int) + 10
  } yield a + b

  addStuff(3)
}
// res2: Int = 19

Both (*2) and (+10) get applied to the number 3 in this case. return (a+b) does as well, but it ignores it and always presents a+b as the result. For this reason, the function monad is also called the reader monad. All the functions read from a common source.

The Reader monad lets us pretend the value is already there. I am guessing that this works only for functions that accepts one parameter.

Dependency injection 

At nescala 2012 on March 9th, Rúnar (@runarorama) gave a talk Dead-Simple Dependency Injection. One of the ideas presented there was to use the Reader monad for dependency injection. Later that year, he also gave a longer version of the talk Lambda: The Ultimate Dependency Injection Framework in YOW 2012. In 2013, Jason Arhart wrote Scrap Your Cake Pattern Boilerplate: Dependency Injection Using the Reader Monad, which I’m going to base my example on.

Imagine we have a case class for a user, and a trait that abstracts the data store to get them.

case class User(id: Long, parentId: Long, name: String, email: String)

trait UserRepo {
  def get(id: Long): User
  def find(name: String): User
}

Next we define a primitive reader for each operation defined in the UserRepo trait:

trait Users {
  def getUser(id: Long): UserRepo => User = {
    case repo => repo.get(id)
  }
  def findUser(name: String): UserRepo => User = {
    case repo => repo.find(name)
  }
}

That looks like boilerplate. (I thought we are scrapping it.) Moving on.

Based on the primitive readers, we can compose other readers, including the application.

object UserInfo extends Users {
  def userInfo(name: String): UserRepo => Map[String, String] =
    for {
      user <- findUser(name)
      boss <- getUser(user.parentId)
    } yield Map(
      "name" -> s"${user.name}",
      "email" -> s"${user.email}",
      "boss_name" -> s"${boss.name}"
    )
}
trait Program {
  def app: UserRepo => String =
    for {
      fredo <- UserInfo.userInfo("Fredo")
    } yield fredo.toString
}

To run this app, we need something that provides an implementation for UserRepo:

val testUsers = List(User(0, 0, "Vito", "vito@example.com"),
  User(1, 0, "Michael", "michael@example.com"),
  User(2, 0, "Fredo", "fredo@example.com"))
// testUsers: List[User] = List(
//   User(id = 0L, parentId = 0L, name = "Vito", email = "vito@example.com"),
//   User(id = 1L, parentId = 0L, name = "Michael", email = "michael@example.com"),
//   User(id = 2L, parentId = 0L, name = "Fredo", email = "fredo@example.com")
// )

object Main extends Program {
  def run: String = app(mkUserRepo)
  def mkUserRepo: UserRepo = new UserRepo {
    def get(id: Long): User = (testUsers find { _.id === id }).get
    def find(name: String): User = (testUsers find { _.name === name }).get
  }
}

Main.run
// res3: String = "Map(name -> Fredo, email -> fredo@example.com, boss_name -> Vito)"

We got the boss man’s name.

We can try using actM instead of a for comprehension:

object UserInfo extends Users {
  import example.MonadSyntax._
  def userInfo(name: String): UserRepo => Map[String, String] =
    actM[UserRepo => *, Map[String, String]] {
      val user = findUser(name).next
      val boss = getUser(user.parentId).next
      Map(
        "name" -> s"${user.name}",
        "email" -> s"${user.email}",
        "boss_name" -> s"${boss.name}"
      )
    }
}

trait Program {
  import example.MonadSyntax._
  def app: UserRepo => String =
    actM[UserRepo => *, String] {
      val fredo = UserInfo.userInfo("Fredo").next
      fredo.toString
    }
}

object Main extends Program {
  def run: String = app(mkUserRepo)
  def mkUserRepo: UserRepo = new UserRepo {
    def get(id: Long): User = (testUsers find { _.id === id }).get
    def find(name: String): User = (testUsers find { _.name === name }).get
  }
}

Main.run
// res5: String = "Map(name -> Fredo, email -> fredo@example.com, boss_name -> Vito)"

The code inside of the actM block looks more natural than the for version, but the type annotations probably make it more difficult to use.

That’s all for today.

day 7 

On day 6 we compared Scala’s for comprehension with Haskell’s do, and implemented the actM macro. We also looked at the Reader datatype, which is another way of thinking about Function1[A, B].

I had been a bit sloppy by describing List and Reader as monads, but I want to correctly say List datatype and Reader datatype, which form a monad under some operation.

State datatype 

When writing code using an immutable data structure, one pattern that arises often is passing of a value that represents some state. The example I like to use is Tetris. Imagine a functional implementation of Tetris where Tetrix.init creates the initial state, and then various transition functions return a transformed state and some return value:

val (s0, _) = Tetrix.init()
val (s1, _) = Tetrix.nextBlock(s0)
val (s2, moved0) = Tetrix.moveBlock(s1, LEFT)
val (s3, moved1) =
  if (moved0) Tetrix.moveBlock(s2, LEFT)
  else (s2, moved0)

The passing of the state objects (s0, s1, s2, …) becomes error-prone boilerplate. The goal is to automate the explicit passing of the states.

To follow along the book, we’ll use the stack example from the book. Here’s an implementation without using State.

import cats._, cats.syntax.all._

type Stack = List[Int]

def pop(s0: Stack): (Stack, Int) =
  s0 match {
    case x :: xs => (xs, x)
    case Nil     => sys.error("stack is empty")
  }

def push(s0: Stack, a: Int): (Stack, Unit) = (a :: s0, ())

def stackManip(s0: Stack): (Stack, Int) = {
  val (s1, _) = push(s0, 3)
  val (s2, a) = pop(s1)
  pop(s2)
}

stackManip(List(5, 8, 2, 1))
// res0: (Stack, Int) = (List(8, 2, 1), 5)

State and StateT datatype 

Learn You a Haskell for Great Good says:

Haskell features the State monad, which makes dealing with stateful problems a breeze while still keeping everything nice and pure. ….

We’ll say that a stateful computation is a function that takes some state and returns a value along with some new state. That function would have the following type:

s -> (a, s)

State is a datatype that encapsulates a stateful computation: S => (S, A). State forms a monad which passes along the states represented by the type S. Haskell should’ve named this Stater or Program to avoid the confusion, but now people already know this by State, so it’s too late.

Cody Allen (@ceedubs) had a pull request open for State/StateT on Cats #302, which was merged recently. (Thanks, Erik) As it happens, State is just a type alias:

package object data {
  ....
  type State[S, A] = StateT[Eval, S, A]
  object State extends StateFunctions
}

StateT is a monad transformer, a type constructor for other datatypes. State partially applies StateT with Eval, which emulates a call stack with heap memory to prevent overflow. Here’s the definition of StateT:

final class StateT[F[_], S, A](val runF: F[S => F[(S, A)]]) {
  ....
}

object StateT extends StateTInstances {
  def apply[F[_], S, A](f: S => F[(S, A)])(implicit F: Applicative[F]): StateT[F, S, A] =
    new StateT(F.pure(f))

  def applyF[F[_], S, A](runF: F[S => F[(S, A)]]): StateT[F, S, A] =
    new StateT(runF)

  /**
   * Run with the provided initial state value
   */
  def run(initial: S)(implicit F: FlatMap[F]): F[(S, A)] =
    F.flatMap(runF)(f => f(initial))

  ....
}

To construct a State value, you pass the state transition function to State.apply.

private[data] abstract class StateFunctions {
  def apply[S, A](f: S => (S, A)): State[S, A] =
    StateT.applyF(Now((s: S) => Now(f(s))))
  
  ....
}

As the State implementation is fresh, a few bumps on the road are expected. When I tried using State on the REPL, I ran into an odd behavior where I can create one state, but not the second. @retronym pointed me to SI-7139: Type alias and object with the same name cause type mismatch in REPL, which I was able to workaround as #322.

Let’s consider how to implement stack with State:

type Stack = List[Int]

import cats._, cats.data._, cats.syntax.all._

val pop = State[Stack, Int] {
  case x :: xs => (xs, x)
  case Nil     => sys.error("stack is empty")
}
// pop: State[Stack, Int] = cats.data.IndexedStateT@3c5c0f3e

def push(a: Int) = State[Stack, Unit] {
  case xs => (a :: xs, ())
}

These are the primitive programs. Now we can construct compound programs by composing the monad.

def stackManip: State[Stack, Int] = for {
  _ <- push(3)
  a <- pop
  b <- pop
} yield(b)

stackManip.run(List(5, 8, 2, 1)).value
// res2: (Stack, Int) = (List(8, 2, 1), 5)

The first run is for StateT, and the second is to run until the end Eval.

Both push and pop are still purely functional, and we were able to eliminate explicitly passing the state object (s0, s1, …).

Getting and setting the state 

LYAHFGG:

The Control.Monad.State module provides a type class that’s called MonadState and it features two pretty useful functions, namely get and put.

The State object defines a few helper functions:

private[data] abstract class StateFunctions {

  def apply[S, A](f: S => (S, A)): State[S, A] =
    StateT.applyF(Now((s: S) => Now(f(s))))

  /**
   * Return `a` and maintain the input state.
   */
  def pure[S, A](a: A): State[S, A] = State(s => (s, a))

  /**
   * Modify the input state and return Unit.
   */
  def modify[S](f: S => S): State[S, Unit] = State(s => (f(s), ()))

  /**
   * Inspect a value from the input state, without modifying the state.
   */
  def inspect[S, T](f: S => T): State[S, T] = State(s => (s, f(s)))

  /**
   * Return the input state without modifying it.
   */
  def get[S]: State[S, S] = inspect(identity)

  /**
   * Set the state to `s` and return Unit.
   */
  def set[S](s: S): State[S, Unit] = State(_ => (s, ()))
}

These are confusing at first. But remember that the State monad encapsulates a pair of a state transition function and a return value. So State.get keeps the state as is, and returns it.

Similarly, State.set(s) in this context means to overwrite the state with s and return ().

Let’s try using them with the stackyStack example from the book:

type Stack = List[Int]

import cats._, cats.data._, cats.syntax.all._

def stackyStack: State[Stack, Unit] = for {
  stackNow <- State.get[Stack]
  r <- if (stackNow === List(1, 2, 3)) State.set[Stack](List(8, 3, 1))
       else State.set[Stack](List(9, 2, 1))
} yield r

stackyStack.run(List(1, 2, 3)).value
// res4: (Stack, Unit) = (List(8, 3, 1), ())

We can also implement both pop and push in terms of get and set:

val pop: State[Stack, Int] = for {
  s <- State.get[Stack]
  (x :: xs) = s
  _ <- State.set[Stack](xs)
} yield x
// pop: State[Stack, Int] = cats.data.IndexedStateT@4fae4cb5

def push(x: Int): State[Stack, Unit] = for {
  xs <- State.get[Stack]
  r <- State.set(x :: xs)
} yield r

As you can see, the State monad on its own doesn’t do much (encapsulate a state transition function and a return value), but by chaining them we can remove some boilerplates.

Extracting and modifying the state 

State.extract(f) and State.modify(f) are slightly more advanced variants of State.get and State.set(s).

State.extract(f) applies the function f: S => T to s, and returns the result without modifying the state itself.

State.modify applies the function f: S => T to s, saves the result as the new state, and returns ().

Validated datatype 

LYAHFGG:

The Either e a type on the other hand, allows us to incorporate a context of possible failure to our values while also being able to attach values to the failure, so that they can describe what went wrong or provide some other useful info regarding the failure.

We know Either[A, B] from the standard library, and we’ve covered that Cats implements a right-biased functor for it too.

There’s another datatype in Cats that we can use in place of Either called Validated:

sealed abstract class Validated[+E, +A] extends Product with Serializable {

  def fold[B](fe: E => B, fa: A => B): B =
    this match {
      case Invalid(e) => fe(e)
      case Valid(a) => fa(a)
    }

  def isValid: Boolean = fold(_ => false, _ => true)
  def isInvalid: Boolean = fold(_ => true, _ => false)

  ....
}

object Validated extends ValidatedInstances with ValidatedFunctions{
  final case class Valid[+A](a: A) extends Validated[Nothing, A]
  final case class Invalid[+E](e: E) extends Validated[E, Nothing]
}

Here’s how to create the values:

import cats._, cats.data._, cats.syntax.all._
import Validated.{ valid, invalid }

valid[String, String]("event 1 ok")
// res0: Validated[String, String] = Valid(a = "event 1 ok")

invalid[String, String]("event 1 failed!")
// res1: Validated[String, String] = Invalid(e = "event 1 failed!")

What’s different about Validated is that it is does not form a monad, but forms an applicative functor. Instead of chaining the result from first event to the next, Validated validates all events:

val result = (valid[String, String]("event 1 ok"),
  invalid[String, String]("event 2 failed!"),
  invalid[String, String]("event 3 failed!")) mapN {_ + _ + _}
// result: Validated[String, String] = Invalid(
//   e = "event 2 failed!event 3 failed!"
// )

The final result is Invalid(event 2 failed!event 3 failed!). Unlike the Xor’s monad, which cuts the calculation short, Validated keeps going to report back all failures. This would be useful for validating user input on an online bacon shop.

The problem, however, is that the error messages are mushed together into one string. Shouldn’t it be something like a list?

Using NonEmptyList to accumulate failures 

This is where NonEmptyList datatype comes in handy. For now, think of it as a list that’s guaranteed to have at least one element.

import cats.data.{ NonEmptyList => NEL }

NEL.of(1)
// res2: NonEmptyList[Int] = NonEmptyList(head = 1, tail = List())

We can use NEL[A] on the invalid side to accumulate the errors:

val result2 =
  (valid[NEL[String], String]("event 1 ok"),
    invalid[NEL[String], String](NEL.of("event 2 failed!")),
    invalid[NEL[String], String](NEL.of("event 3 failed!"))) mapN {_ + _ + _}
// result2: Validated[NonEmptyList[String], String] = Invalid(
//   e = NonEmptyList(head = "event 2 failed!", tail = List("event 3 failed!"))
// )

Inside Invalid, we were able to accumulate all failed messages.

We can use the fold method to extract the values:

val errs: NEL[String] = result2.fold(
  { l => l },
  { r => sys.error("invalid is expected") }
)
// errs: NonEmptyList[String] = NonEmptyList(
//   head = "event 2 failed!",
//   tail = List("event 3 failed!")
// )

Ior datatype 

In Cats there is yet another datatype that represents an A-B pair called Ior.

/** Represents a right-biased disjunction that is either an `A`, or a `B`, or both an `A` and a `B`.
 *
 * An instance of `A [[Ior]] B` is one of:
 *  - `[[Ior.Left Left]][A]`
 *  - `[[Ior.Right Right]][B]`
 *  - `[[Ior.Both Both]][A, B]`
 *
 * `A [[Ior]] B` is similar to `A [[Xor]] B`, except that it can represent the simultaneous presence of
 * an `A` and a `B`. It is right-biased like [[Xor]], so methods such as `map` and `flatMap` operate on the
 * `B` value. Some methods, like `flatMap`, handle the presence of two [[Ior.Both Both]] values using a
 * `[[Semigroup]][A]`, while other methods, like [[toXor]], ignore the `A` value in a [[Ior.Both Both]].
 *
 * `A [[Ior]] B` is isomorphic to `(A [[Xor]] B) [[Xor]] (A, B)`, but provides methods biased toward `B`
 * values, regardless of whether the `B` values appear in a [[Ior.Right Right]] or a [[Ior.Both Both]].
 * The isomorphic [[Xor]] form can be accessed via the [[unwrap]] method.
 */
sealed abstract class Ior[+A, +B] extends Product with Serializable {

  final def fold[C](fa: A => C, fb: B => C, fab: (A, B) => C): C = this match {
    case Ior.Left(a) => fa(a)
    case Ior.Right(b) => fb(b)
    case Ior.Both(a, b) => fab(a, b)
  }

  final def isLeft: Boolean = fold(_ => true, _ => false, (_, _) => false)
  final def isRight: Boolean = fold(_ => false, _ => true, (_, _) => false)
  final def isBoth: Boolean = fold(_ => false, _ => false, (_, _) => true)

  ....
}

object Ior extends IorInstances with IorFunctions {
  final case class Left[+A](a: A) extends (A Ior Nothing)
  final case class Right[+B](b: B) extends (Nothing Ior B)
  final case class Both[+A, +B](a: A, b: B) extends (A Ior B)
}

These values are created using the left, right, and both methods on Ior:

import cats._, cats.data._, cats.syntax.all._

import cats.data.{ NonEmptyList => NEL }

Ior.right[NEL[String], Int](1)
// res0: Ior[NonEmptyList[String], Int] = Right(b = 1)

Ior.left[NEL[String], Int](NEL.of("error"))
// res1: Ior[NonEmptyList[String], Int] = Left(
//   a = NonEmptyList(head = "error", tail = List())
// )

Ior.both[NEL[String], Int](NEL.of("warning"), 1)
// res2: Ior[NonEmptyList[String], Int] = Both(
//   a = NonEmptyList(head = "warning", tail = List()),
//   b = 1
// )

As noted in the scaladoc comment, Ior’s flatMap uses Semigroup[A] to accumulate failures when it sees an Ior.both(...) value. So we could probably use this as a hybrid of Xor and Validated.

Here’s how flatMap behaves for all nine combinations:

Ior.right[NEL[String], Int](1) >>=
  { x => Ior.right[NEL[String], Int](x + 1) }
// res3: Ior[NonEmptyList[String], Int] = Right(b = 2)

Ior.left[NEL[String], Int](NEL.of("error 1")) >>=
  { x => Ior.right[NEL[String], Int](x + 1) }
// res4: Ior[NonEmptyList[String], Int] = Left(
//   a = NonEmptyList(head = "error 1", tail = List())
// )

Ior.both[NEL[String], Int](NEL.of("warning 1"), 1) >>=
  { x => Ior.right[NEL[String], Int](x + 1) }
// res5: Ior[NonEmptyList[String], Int] = Both(
//   a = NonEmptyList(head = "warning 1", tail = List()),
//   b = 2
// )

Ior.right[NEL[String], Int](1) >>=
  { x => Ior.left[NEL[String], Int](NEL.of("error 2")) }
// res6: Ior[NonEmptyList[String], Int] = Left(
//   a = NonEmptyList(head = "error 2", tail = List())
// )

Ior.left[NEL[String], Int](NEL.of("error 1")) >>=
  { x => Ior.left[NEL[String], Int](NEL.of("error 2")) }
// res7: Ior[NonEmptyList[String], Int] = Left(
//   a = NonEmptyList(head = "error 1", tail = List())
// )

Ior.both[NEL[String], Int](NEL.of("warning 1"), 1) >>=
  { x => Ior.left[NEL[String], Int](NEL.of("error 2")) }
// res8: Ior[NonEmptyList[String], Int] = Left(
//   a = NonEmptyList(head = "warning 1", tail = List("error 2"))
// )

Ior.right[NEL[String], Int](1) >>=
  { x => Ior.both[NEL[String], Int](NEL.of("warning 2"), x + 1) }
// res9: Ior[NonEmptyList[String], Int] = Both(
//   a = NonEmptyList(head = "warning 2", tail = List()),
//   b = 2
// )

Ior.left[NEL[String], Int](NEL.of("error 1")) >>=
  { x => Ior.both[NEL[String], Int](NEL.of("warning 2"), x + 1) }
// res10: Ior[NonEmptyList[String], Int] = Left(
//   a = NonEmptyList(head = "error 1", tail = List())
// )

Ior.both[NEL[String], Int](NEL.of("warning 1"), 1) >>=
  { x => Ior.both[NEL[String], Int](NEL.of("warning 2"), x + 1) }
// res11: Ior[NonEmptyList[String], Int] = Both(
//   a = NonEmptyList(head = "warning 1", tail = List("warning 2")),
//   b = 2
// )

Let’s try using it in for comprehension:

for {
  e1 <- Ior.right[NEL[String], Int](1)
  e2 <- Ior.both[NEL[String], Int](NEL.of("event 2 warning"), e1 + 1)
  e3 <- Ior.both[NEL[String], Int](NEL.of("event 3 warning"), e2 + 1)
} yield (e1 |+| e2 |+| e3)
// res12: Ior[NonEmptyList[String], Int] = Both(
//   a = NonEmptyList(head = "event 2 warning", tail = List("event 3 warning")),
//   b = 6
// )

So Ior.left short curcuits like the failure values in Xor[A, B] and Either[A, B], but Ior.both accumulates the failure values like Validated[A, B].

That’s it for today! We’ll pick it up from here later.

day 8 

On day 7 we looked at the State datatype, which encapsulates stateful computation. We also looked at two alternatives for Either[A, B]: the Xor datatype, the Validated datatype, and the Ior datatype.

Free monoids 

I’m going to diverge from Learn You a Haskell for Great Good a bit, and explore free objects.

Let’s first look into free monoids. Given a set of characters:

A = { 'a', 'b', 'c', ... }

We can form the free monoid on A called A* as follows:

A* = String

Here, the binary operation is String concatenation + operator. We can show that this satisfies the monoid laws using the empty string "" as the identity.

Furthermore, a free monoid can be formed from any arbitrary set A by concatenating them:

A* = List[A]

Here, the binary operation is :::, and the identity is Nil. The definition of the free monoid M(A) is given as follows:

Awodey:

Universal Mapping Property of M(A)
There is a function i: A => |M(A)|, and given any monoid N and any function f: A => |N|, there is a unique monoid homomorphism f_hom = M(A) => N such that |f_hom| ∘ i = f, all as indicated in the following diagram:

Instead of A, I’ll use X here. Also |N| means Set[N]:

If we think in terms of Scala,

def i(x: X): Set[M[X]] = ???
def f(x: X): Set[N] = ???

// there exists a unique
def f_hom(mx: M[X]): N

// such that
def f_hom_set(smx: Set[M[X]]): Set[N] = smx map {f_hom}
f == f_hom_set compose i

Suppose A is Char and N is (Int, +). We can write a property test to see if String is a free monoid.

scala> def i(x: Char): Set[String] = Set(x.toString)
i: (x: Char)Set[String]

scala> def f(x: Char): Set[Int] = Set(x.toInt) // example
f: (x: Char)Set[Int]

scala> val f_hom: PartialFunction[String, Int] =
         { case mx: String if mx.size == 1 => mx.charAt(0).toInt }
f_hom: PartialFunction[String,Int] = <function1>

scala> def f_hom_set(smx: Set[String]): Set[Int] = smx map {f_hom}
f_hom_set: (smx: Set[String])Set[Int]

scala> val g = (f_hom_set _) compose (i _)
g: Char => Set[Int] = <function1>

scala> import org.scalacheck.Prop.forAll
import org.scalacheck.Prop.forAll

scala> val propMAFree = forAll { c: Char => f(c) == g(c) }
propMAFree: org.scalacheck.Prop = Prop

scala> propMAFree.check
+ OK, passed 100 tests.

At least for this implemention of f we were able to show that String is free.

Injective 

This intuitively shows that Set[M[X]] needs to be lossless for X to allow any f, meaning no two values on X can map into the same value in M[X]. In algebra, this is expressed as i is injective for arrows from Char.

Definitions: An arrow f satisfying the property ‘for any pair of arrows x₁: T => A and x₂: T => A, if f ∘ x₁ = f ∘ x₂ then x₁ = x₂‘, it is said to be injective for arrows from T.

Uniqueness 

UMP also stipulates f_hom to be unique, so that requires Set[M[A]] to be zero or more combinations of A’s and nothing more. Because M[A] is unique for A, conceptually there is one and only free monoid for a set A. We can however have the free monoid expressed in different ways like String and List[Char], so it ends up being more like a free monoid.

Free objects 

It turns out that the free monoid is an example of free objects, which we can define using a functor Set[A]: C[A] => Set[A].

Comparing the diagram, we see that they are mostly similar.

Free monads 

We said that free monoids are examples of free objects. Similarly, free monads are examples of free objects.

I’m not going to get into the details, monad is a monoid in the category of endofunctors F: C => C, using F × F => F as the binary operator. Similar to the way we could derive A* from A, we can derive the free monad F* for a given endofunctor F.

Here’s how Haskell does it:

data Free f a = Pure a | Free (f (Free f a))

instance Functor f => Monad (Free f) where
  return = Pure
  Pure a >>= f = f a
  Free m >>= f = Free ((>>= f) <$> m)

Wikipedia on Monad:

Unlike List, which stores a list of values, Free stores a list of functors, wrapped around an initial value. Accordingly, the Functor and Monad instances of Free do nothing other than handing a given function down that list with fmap.

Also note that Free is a datatype, but there are different free monads that gets formed for each Functor.

Why free monads matter 

In practice, we can view Free as a clever way of forming Monad out of Functor. This is particularly useful for interpreter pattern, which is explained by Gabriel Gonzalez (@gabrielg439)’s Why free monads matter:

Let’s try to come up with some sort of abstraction that represents the essence of a syntax tree. …

Our toy language will only have three commands:

output b -- prints a "b" to the console
bell     -- rings the computer's bell
done     -- end of execution

So we represent it as a syntax tree where subsequent commands are leaves of prior commands:

data Toy b next =
    Output b next
  | Bell next
  | Done

Here’s Toy translated into Scala as is:

sealed trait Toy[+A, +Next]

object Toy {
  case class Output[A, Next](a: A, next: Next) extends Toy[A, Next]
  case class Bell[Next](next: Next) extends Toy[Nothing, Next]
  case class Done() extends Toy[Nothing, Nothing]
}

Toy.Output('A', Toy.Done())
// res0: Toy.Output[Char, Toy.Done] = Output(a = 'A', next = Done())

Toy.Bell(Toy.Output('A', Toy.Done()))
// res1: Toy.Bell[Toy.Output[Char, Toy.Done]] = Bell(
//   next = Output(a = 'A', next = Done())
// )

CharToy 

In WFMM’s original DSL, Output b next has two type parameters b and next. This allows Output to be generic about the output type. As demonstrated above as Toy, Scala can do this too. But doing so unnecessarily complicates the demonstration of Free because of Scala’s handling of partially applied types. So we’ll first hardcode the datatype to Char as follows:

sealed trait CharToy[+Next]

object CharToy {
  case class CharOutput[Next](a: Char, next: Next) extends CharToy[Next]
  case class CharBell[Next](next: Next) extends CharToy[Next]
  case class CharDone() extends CharToy[Nothing]

  def output[Next](a: Char, next: Next): CharToy[Next] = CharOutput(a, next)
  def bell[Next](next: Next): CharToy[Next] = CharBell(next)
  def done: CharToy[Nothing] = CharDone()
}

{
  import CharToy._
  output('A', done)
}
// res2: CharToy[CharToy[Nothing]] = CharOutput(a = 'A', next = CharDone())

{
  import CharToy._
  bell(output('A', done))
}
// res3: CharToy[CharToy[CharToy[Nothing]]] = CharBell(
//   next = CharOutput(a = 'A', next = CharDone())
// )

I’ve added helper functions lowercase output, bell, and done to unify the types to CharToy.

Fix 

WFMM:

but unfortunately this doesn’t work because every time I want to add a command, it changes the type.

Let’s define Fix:

case class Fix[F[_]](f: F[Fix[F]])

object Fix {
  def fix(toy: CharToy[Fix[CharToy]]) = Fix[CharToy](toy)
}

{
  import Fix._, CharToy._
  fix(output('A', fix(done)))
}
// res4: Fix[CharToy] = Fix(
//   f = CharOutput(a = 'A', next = Fix(f = CharDone()))
// )

{
  import Fix._, CharToy._
  fix(bell(fix(output('A', fix(done)))))
}
// res5: Fix[CharToy] = Fix(
//   f = CharBell(next = Fix(f = CharOutput(a = 'A', next = Fix(f = CharDone()))))
// )

Again, fix is provided so that the type inference works.

FixE 

We are also going to try to implement FixE, which adds an exception to this. Since throw and catch are reserved, I am renaming them to throwy and catchy:

import cats._, cats.data._, cats.syntax.all._

sealed trait FixE[F[_], E]
object FixE {
  case class Fix[F[_], E](f: F[FixE[F, E]]) extends FixE[F, E]
  case class Throwy[F[_], E](e: E) extends FixE[F, E]

  def fix[E](toy: CharToy[FixE[CharToy, E]]): FixE[CharToy, E] =
    Fix[CharToy, E](toy)
  def throwy[F[_], E](e: E): FixE[F, E] = Throwy(e)
  def catchy[F[_]: Functor, E1, E2](ex: => FixE[F, E1])
      (f: E1 => FixE[F, E2]): FixE[F, E2] = ex match {
    case Fix(x)    => Fix[F, E2](Functor[F].map(x) {catchy(_)(f)})
    case Throwy(e) => f(e)
  }
}

We can only use this if Toy b is a functor, so we muddle around until we find something that type-checks (and satisfies the Functor laws).

Let’s define Functor for CharToy:

implicit val charToyFunctor: Functor[CharToy] = new Functor[CharToy] {
  def map[A, B](fa: CharToy[A])(f: A => B): CharToy[B] = fa match {
    case o: CharToy.CharOutput[A] => CharToy.CharOutput(o.a, f(o.next))
    case b: CharToy.CharBell[A]   => CharToy.CharBell(f(b.next))
    case CharToy.CharDone()       => CharToy.CharDone()
  }
}
// charToyFunctor: Functor[CharToy] = repl.MdocSession1@2629300

Here’s a sample usage:

{
  import FixE._, CharToy._
  case class IncompleteException()
  def subroutine = fix[IncompleteException](
    output('A',
      throwy[CharToy, IncompleteException](IncompleteException())))
  def program = catchy[CharToy, IncompleteException, Nothing](subroutine) { _ =>
    fix[Nothing](bell(fix[Nothing](done)))
  }
}

The fact that we need to supply type parameters everywhere is a bit unfortunate.

Free datatype 

WFMM:

our FixE already exists, too, and it’s called the Free monad:

data Free f r = Free (f (Free f r)) | Pure r

As the name suggests, it is automatically a monad (if f is a functor):

instance (Functor f) => Monad (Free f) where
    return = Pure
    (Free x) >>= f = Free (fmap (>>= f) x)
    (Pure r) >>= f = f r

The return was our Throw, and (>>=) was our catch.

The datatype in Cats is called Free:

/**
 * A free operational monad for some functor `S`. Binding is done
 * using the heap instead of the stack, allowing tail-call
 * elimination.
 */
sealed abstract class Free[S[_], A] extends Product with Serializable {

  final def map[B](f: A => B): Free[S, B] =
    flatMap(a => Pure(f(a)))

  /**
   * Bind the given continuation to the result of this computation.
   * All left-associated binds are reassociated to the right.
   */
  final def flatMap[B](f: A => Free[S, B]): Free[S, B] =
    Gosub(this, f)

  ....
}

object Free {
  /**
   * Return from the computation with the given value.
   */
  private final case class Pure[S[_], A](a: A) extends Free[S, A]

  /** Suspend the computation with the given suspension. */
  private final case class Suspend[S[_], A](a: S[A]) extends Free[S, A]

  /** Call a subroutine and continue with the given function. */
  private final case class Gosub[S[_], B, C](c: Free[S, C], f: C => Free[S, B]) extends Free[S, B]

  /**
   * Suspend a value within a functor lifting it to a Free.
   */
  def liftF[F[_], A](value: F[A]): Free[F, A] = Suspend(value)

  /** Suspend the Free with the Applicative */
  def suspend[F[_], A](value: => Free[F, A])(implicit F: Applicative[F]): Free[F, A] =
    liftF(F.pure(())).flatMap(_ => value)

  /** Lift a pure value into Free */
  def pure[S[_], A](a: A): Free[S, A] = Pure(a)

  final class FreeInjectPartiallyApplied[F[_], G[_]] private[free] {
    def apply[A](fa: F[A])(implicit I : Inject[F, G]): Free[G, A] =
      Free.liftF(I.inj(fa))
  }

  def inject[F[_], G[_]]: FreeInjectPartiallyApplied[F, G] = new FreeInjectPartiallyApplied

  ....
}

To use these datatypes in Cats, use Free.liftF:

import cats.free.Free

sealed trait CharToy[+Next]
object CharToy {
  case class CharOutput[Next](a: Char, next: Next) extends CharToy[Next]
  case class CharBell[Next](next: Next) extends CharToy[Next]
  case class CharDone() extends CharToy[Nothing]

  implicit val charToyFunctor: Functor[CharToy] = new Functor[CharToy] {
    def map[A, B](fa: CharToy[A])(f: A => B): CharToy[B] = fa match {
        case o: CharOutput[A] => CharOutput(o.a, f(o.next))
        case b: CharBell[A]   => CharBell(f(b.next))
        case CharDone()       => CharDone()
      }
    }
  def output(a: Char): Free[CharToy, Unit] =
    Free.liftF[CharToy, Unit](CharOutput(a, ()))
  def bell: Free[CharToy, Unit] = Free.liftF[CharToy, Unit](CharBell(()))
  def done: Free[CharToy, Unit] = Free.liftF[CharToy, Unit](CharDone())
  def pure[A](a: A): Free[CharToy, A] = Free.pure[CharToy, A](a)
}

Here’s the command sequence:

import CharToy._

val subroutine = output('A')
// subroutine: Free[CharToy, Unit] = Suspend(
//   a = CharOutput(a = 'A', next = ())
// )

val program = for {
  _ <- subroutine
  _ <- bell
  _ <- done
} yield ()
// program: Free[CharToy, Unit] = FlatMapped(
//   c = Suspend(a = CharOutput(a = 'A', next = ())),
//   f = <function1>
// )

This is where things get magical. We now have do notation for something that hasn’t even been interpreted yet: it’s pure data.

Next we’d like to define showProgram to prove that what we have is just data:

def showProgram[R: Show](p: Free[CharToy, R]): String =
  p.fold({ r: R => "return " + Show[R].show(r) + "\n" },
    {
      case CharOutput(a, next) =>
        "output " + Show[Char].show(a) + "\n" + showProgram(next)
      case CharBell(next) =>
        "bell " + "\n" + showProgram(next)
      case CharDone() =>
        "done\n"
    })

showProgram(program)
// res8: String = """output A
// bell 
// done
// """

We can manually check that the monad generated using Free satisfies the monad laws:

showProgram(output('A'))
// res9: String = """output A
// return ()
// """

showProgram(pure('A') flatMap output)
// res10: String = """output A
// return ()
// """

showProgram(output('A') flatMap pure)
// res11: String = """output A
// return ()
// """

showProgram((output('A') flatMap { _ => done }) flatMap { _ => output('C') })
// res12: String = """output A
// done
// """

showProgram(output('A') flatMap { _ => (done flatMap { _ => output('C') }) })
// res13: String = """output A
// done
// """

Looking good. Notice the abort-like semantics of done. Also, due to type inference limitation, I was not able to use >>= and >> here.

WFMM:

The free monad is the interpreter’s best friend. Free monads “free the interpreter” as much as possible while still maintaining the bare minimum necessary to form a monad.

Another way of looking at it is that the Free datatype provides a way of building a syntax tree given a container.

One of the reasons the Free datatype is gaining popularity I think is that people are running into the limitation of combining different monads. It’s not impossible with monad transformer, but the type signature gets hairy quickly, and the stacking leaks into various places in code. On the other hand, Free essentially gives up on encoding meaning into the monad. You gain flexibility because you can do whatever in the interpreter function, for instance run sequentially during testing, but run in parallel for production.

Stackless Scala with Free Monads 

The notion of free monad goes beyond just the interpreter pattern. I think people are still discovering new ways of harnessing its power.

Rúnar (@runarorama) has been a proponent of using Free in Scala. His talk that we covered on day 6, Dead-Simple Dependency Injection, uses Free to implement a mini language to implement a key-value store. The same year, Rúnar also gave a talk at Scala Days 2012 called Stackless Scala With Free Monads. I recommend watching the talk before reading the paper, but it’s easier to quote the paper version, Stackless Scala With Free Monads.

Rúnar starts out with code that uses an implementation of the State monad to zip a list with its indices. It blows the stack when the list is larger than the stack limit. Then he introduces trampoline, which is a single loop that drives the entire program.

sealed trait Trampoline [+ A] {
  final def runT : A =
    this match {
      case More (k) => k().runT
      case Done (v) => v
    }
}
case class More[+A](k: () => Trampoline[A])
  extends Trampoline[A]
case class Done [+A](result: A)
  extends Trampoline [A]

In the above code, Function0 k is used as a thunk for the next step.

To extend its usage for State monad, he then reifies flatMap into a data structure called FlatMap:

case class FlatMap [A,+B](
  sub: Trampoline [A],
  k: A => Trampoline[B]) extends Trampoline[B]

Next, it is revealed that Trampoline is a free monad of Function0. Here’s how it’s defined in Cats:

  type Trampoline[A] = Free[Function0, A]

Trampoline 

Using Trampoline any program can be transformed into a stackless one. Trampoline object defines a few useful functions for trampolining:

object Trampoline {
  def done[A](a: A): Trampoline[A] =
    Free.Pure[Function0,A](a)

  def defer[A](a: => Trampoline[A]): Trampoline[A] =
    Free.defer(a)

  def delay[A](a: => A): Trampoline[A] =
    suspend(done(a))
}

Let’s try implementing even and odd from the talk:

import cats._, cats.syntax.all._, cats.free.{ Free, Trampoline }
import Trampoline._

def even[A](ns: List[A]): Trampoline[Boolean] =
  ns match {
    case Nil     => done(true)
    case x :: xs => defer(odd(xs))
  }

def odd[A](ns: List[A]): Trampoline[Boolean] =
  ns match {
    case Nil     => done(false)
    case x :: xs => defer(even(xs))
  }

even(List(1, 2, 3)).run
// res0: Boolean = false

even((0 to 3000).toList).run
// res1: Boolean = false

While implementing the above I ran into SI-7139 again, so I had to tweak the Cats’ code. #322

Free monads 

In addition, Rúnar introduces several datatypes that can be derived using Free:

type Pair[+A] = (A, A)
type BinTree[+A] = Free[Pair, A]

type Tree[+A] = Free[List, A]

type FreeMonoid[+A] = Free[({type λ[+α] = (A,α)})#λ, Unit]

type Trivial[+A] = Unit
type Option[+A] = Free[Trivial, A]

There’s also an iteratees implementation based on free monads. Finally, he summarizes free monads in nice bullet points:

• A model for any recursive data type with data at the leaves.
• A free monad is an expression tree with variables at the leaves and flatMap is variable substitution.

Free monoid using Free 

Let’s try defining “List” using Free.

type FreeMonoid[A] = Free[(A, +*), Unit]

def cons[A](a: A): FreeMonoid[A] =
  Free.liftF[(A, +*), Unit]((a, ()))

val x = cons(1)
// x: FreeMonoid[Int] = Suspend(a = (1, ()))

val xs = cons(1) flatMap { _ => cons(2) }
// xs: Free[(Int, β0), Unit] = FlatMapped(
//   c = Suspend(a = (1, ())),
//   f = <function1>
// )

As a way of interpreting the result, let’s try converting this to a standard List:

implicit def tuple2Functor[A]: Functor[(A, *)] =
  new Functor[(A, *)] {
    def map[B, C](fa: (A, B))(f: B => C) =
      (fa._1, f(fa._2))
  }

def toList[A](list: FreeMonoid[A]): List[A] =
  list.fold(
    { _ => Nil },
    { case (x: A @unchecked, xs: FreeMonoid[A]) => x :: toList(xs) })

toList(xs)
// res2: List[Int] = List(1, 2)

Tail Recursive Monads (FlatMap) 

In 2015 Phil Freeman (@paf31) wrote Stack Safety for Free working with PureScript hosted on JavaScript, a strict language like Scala:

I've written up some work on stack safe free monad transformers. Feedback would be very much appreciated http://t.co/1rH7OwaWpy

— Phil Freeman (@paf31) August 8, 2015

The paper gives a hat tip to Rúnar (@runarorama)’s Stackless Scala With Free Monads, but presents a more drastic solution to the stack safety problem.

The stack problem 

As a background, in Scala the compiler is able to optimize on self-recursive tail calls. For example, here’s an example of a self-recursive tail calls.

import scala.annotation.tailrec

def pow(n: Long, exp: Long): Long =
  {
    @tailrec def go(acc: Long, p: Long): Long =
      (acc, p) match {
        case (acc, 0) => acc
        case (acc, p) => go(acc * n, p - 1)
      }
    go(1, exp)
  }

pow(2, 3)
// res0: Long = 8L

Here’s an example that’s not self-recursive. It’s blowing up the stack.

scala> :paste
object OddEven0 {
  def odd(n: Int): String = even(n - 1)
  def even(n: Int): String = if (n <= 0) "done" else odd(n - 1)
}

// Exiting paste mode, now interpreting.

defined object OddEven0

scala> OddEven0.even(200000)
java.lang.StackOverflowError
  at OddEven0$.even(<console>:15)
  at OddEven0$.odd(<console>:14)
  at OddEven0$.even(<console>:15)
  at OddEven0$.odd(<console>:14)
  at OddEven0$.even(<console>:15)
  ....

Next, we’d try to add Writer datatype to do the pow calculation using LongProduct monoid.

import cats._, cats.data._, cats.syntax.all._

case class LongProduct(value: Long)

implicit val longProdMonoid: Monoid[LongProduct] = new Monoid[LongProduct] {
  def empty: LongProduct = LongProduct(1)
  def combine(x: LongProduct, y: LongProduct): LongProduct = LongProduct(x.value * y.value)
}
// longProdMonoid: Monoid[LongProduct] = repl.MdocSession1@6b0f544

def powWriter(x: Long, exp: Long): Writer[LongProduct, Unit] =
  exp match {
    case 0 => Writer(LongProduct(1L), ())
    case m =>
      Writer(LongProduct(x), ()) >>= { _ => powWriter(x, exp - 1) }
  }

powWriter(2, 3).run
// res1: (LongProduct, Unit) = (LongProduct(value = 8L), ())

This is no longer self-recursive, so it will blow the stack with large exp.

scala> powWriter(1, 10000).run
java.lang.StackOverflowError
  at $anonfun$powWriter$1.apply(<console>:35)
  at $anonfun$powWriter$1.apply(<console>:35)
  at cats.data.WriterT$$anonfun$flatMap$1.apply(WriterT.scala:37)
  at cats.data.WriterT$$anonfun$flatMap$1.apply(WriterT.scala:36)
  at cats.package$$anon$1.flatMap(package.scala:34)
  at cats.data.WriterT.flatMap(WriterT.scala:36)
  at cats.data.WriterTFlatMap1$class.flatMap(WriterT.scala:249)
  at cats.data.WriterTInstances2$$anon$4.flatMap(WriterT.scala:130)
  at cats.data.WriterTInstances2$$anon$4.flatMap(WriterT.scala:130)
  at cats.FlatMap$class.$greater$greater$eq(FlatMap.scala:26)
  at cats.data.WriterTInstances2$$anon$4.$greater$greater$eq(WriterT.scala:130)
  at cats.FlatMap$Ops$class.$greater$greater$eq(FlatMap.scala:20)
  at cats.syntax.FlatMapSyntax1$$anon$1.$greater$greater$eq(flatMap.scala:6)
  at .powWriter1(<console>:35)
  at $anonfun$powWriter$1.apply(<console>:35)

This characteristic of Scala limits the usefulness of monadic composition where flatMap can call monadic function f, which then can call flatMap etc..

FlatMap (MonadRec) 

Our solution is to reduce the candidates for the target monad m from an arbitrary monad, to the class of so-called tail-recursive monads.

class (Monad m) <= MonadRec m where
  tailRecM :: forall a b. (a -> m (Either a b)) -> a -> m b

Here’s the same function in Scala:

  /**
   * Keeps calling `f` until a `scala.util.Right[B]` is returned.
   */
  def tailRecM[A, B](a: A)(f: A => F[Either[A, B]]): F[B]

As it turns out, Oscar Boykin (@posco) brought tailRecM into FlatMap in #1280 (Remove FlatMapRec make all FlatMap implement tailRecM), and it’s now part of Cats 0.7.0. In other words, all FlatMap/Monads in Cats 0.7.0 are tail-recursive.

We can for example, obtain the tailRecM for Writer:

def tailRecM[A, B] = FlatMap[Writer[Vector[String], *]].tailRecM[A, B] _

Here’s how we can make a stack-safe powWriter:

def powWriter2(x: Long, exp: Long): Writer[LongProduct, Unit] =
  FlatMap[Writer[LongProduct, *]].tailRecM(exp) {
    case 0L      => Writer.value[LongProduct, Either[Long, Unit]](Right(()))
    case m: Long => Writer.tell(LongProduct(x)) >>= { _ => Writer.value(Left(m - 1)) }
  }

powWriter2(2, 3).run
// res2: (LongProduct, Unit) = (LongProduct(value = 8L), ())

powWriter2(1, 10000).run
// res3: (LongProduct, Unit) = (LongProduct(value = 1L), ())

This guarantees greater safety on the user of FlatMap typeclass, but it would mean that each the implementers of the instances would need to provide a safe tailRecM.

Here’s the one for Option for example:

@tailrec
def tailRecM[A, B](a: A)(f: A => Option[Either[A, B]]): Option[B] =
  f(a) match {
    case None => None
    case Some(Left(a1)) => tailRecM(a1)(f)
    case Some(Right(b)) => Some(b)
  }

That’s it for today!

day 9 

On day 8 we reviewed the Ior datatype, free monoids, free monads, and the Trampoline datatype. Let’s continue on.

Some useful monadic functions 

Learn You a Haskell for Great Good says:

In this section, we’re going to explore a few functions that either operate on monadic values or return monadic values as their results (or both!). Such functions are usually referred to as monadic functions.

Unlike Haskell’s standard Monad, Cats’ Monad is more granularly designed with the hindsight of weaker typeclasses.

• Monad
• extends FlatMap and Applicative
• extends Apply
• extends Functor

Here there’s no question that all monads are applicative functors as well as functors. This means we can use ap or map operator on the datatypes that form a monad.

flatten method 

LYAHFGG:

It turns out that any nested monadic value can be flattened and that this is actually a property unique to monads. For this, the join function exists.

In Cats, the equivalent function called flatten on FlatMap. Thanks to simulacrum, flatten can also be injected as a method.

@typeclass trait FlatMap[F[_]] extends Apply[F] {
  def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B]

  /**
   * also commonly called join
   */
  def flatten[A](ffa: F[F[A]]): F[A] =
    flatMap(ffa)(fa => fa)

  ....
}

Since Option[A] already implements flatten we need to make an abtract function to turn it into an abtract type.

import cats._, cats.syntax.all._

def join[F[_]: FlatMap, A](fa: F[F[A]]): F[A] =
  fa.flatten

join(1.some.some)
// res0: Option[Int] = Some(value = 1)

If I’m going to make it into a function, I could’ve used the function syntax:

FlatMap[Option].flatten(1.some.some)
// res1: Option[Int] = Some(value = 1)

filterM method 

LYAHFGG:

The filterM function from Control.Monad does just what we want! … The predicate returns a monadic value whose result is a Bool.

Cats does not have filterM, but there’s filterA on TraverseFilter.

foldM function 

LYAHFGG:

The monadic counterpart to foldl is foldM.

I did not find foldM in Cats, so implemented it myself, but it wasn’t stack-safe. Tomas Mikula added a better implementation and that got merged as #925:

  /**
   * Left associative monadic folding on `F`.
   */
  def foldM[G[_], A, B](fa: F[A], z: B)(f: (B, A) => G[B])(implicit G: Monad[G]): G[B] =
    foldLeft(fa, G.pure(z))((gb, a) => G.flatMap(gb)(f(_, a)))

Let’s try using this.

def binSmalls(acc: Int, x: Int): Option[Int] =
  if (x > 9) none[Int] else (acc + x).some

(Foldable[List].foldM(List(2, 8, 3, 1), 0) {binSmalls})
// res2: Option[Int] = Some(value = 14)

(Foldable[List].foldM(List(2, 11, 3, 1), 0) {binSmalls})
// res3: Option[Int] = None

In the above, binSmalls returns None when it finds a number larger than 9.

Making a safe RPN calculator 

LYAHFGG:

When we were solving the problem of implementing a RPN calculator, we noted that it worked fine as long as the input that it got made sense.

We have not covered the chapter on RPN calculator, so let’s translate it into Scala.

def foldingFunction(list: List[Double], next: String): List[Double] =
  (list, next) match {
    case (x :: y :: ys, "*") => (y * x) :: ys
    case (x :: y :: ys, "+") => (y + x) :: ys
    case (x :: y :: ys, "-") => (y - x) :: ys
    case (xs, numString) => numString.toInt :: xs
  }

def solveRPN(s: String): Double =
  (s.split(' ').toList
    .foldLeft(Nil: List[Double]) {foldingFunction}).head

solveRPN("10 4 3 + 2 * -")
// res0: Double = -4.0

Looks like it’s working.

The next step is to change the folding function to handle errors gracefully. We can implement parseInt as follows:

import scala.util.Try

def parseInt(x: String): Option[Int] =
  (scala.util.Try(x.toInt) map { Some(_) }
  recover { case _: NumberFormatException => None }).get

parseInt("1")
// res2: Option[Int] = Some(value = 1)

parseInt("foo")
// res3: Option[Int] = None

Here’s the updated folding function:

import cats._, cats.syntax.all._

def foldingFunction(list: List[Double], next: String): Option[List[Double]] =
  (list, next) match {
    case (x :: y :: ys, "*") => ((y * x) :: ys).some
    case (x :: y :: ys, "+") => ((y + x) :: ys).some
    case (x :: y :: ys, "-") => ((y - x) :: ys).some
    case (xs, numString) => parseInt(numString) map {_ :: xs}
  }

foldingFunction(List(3, 2), "*")
// res4: Option[List[Double]] = Some(value = List(6.0))

foldingFunction(Nil, "*")
// res5: Option[List[Double]] = None

foldingFunction(Nil, "wawa")
// res6: Option[List[Double]] = None

Finally, here’s the updated solveRPN using foldM:

def solveRPN(s: String): Option[Double] =
  for {
    List(x) <- (Foldable[List].foldM(s.split(' ').toList,
                  Nil: List[Double]) {foldingFunction})
  } yield x

solveRPN("1 2 * 4 +")
// res7: Option[Double] = Some(value = 6.0)

solveRPN("1 2 * 4")
// res8: Option[Double] = None

solveRPN("1 8 garbage")
// res9: Option[Double] = None

Composing monadic functions 

LYAHFGG:

When we were learning about the monad laws, we said that the <=< function is just like composition, only instead of working for normal functions like a -> b, it works for monadic functions like a -> m b.

In Cats there’s a special wrapper for a function of type A => F[B] called Kleisli:

/**
 * Represents a function `A => F[B]`.
 */
final case class Kleisli[F[_], A, B](run: A => F[B]) { self =>

  ....
}

object Kleisli extends KleisliInstances with KleisliFunctions

private[data] sealed trait KleisliFunctions {

  def pure[F[_], A, B](x: B)(implicit F: Applicative[F]): Kleisli[F, A, B] =
    Kleisli(_ => F.pure(x))

  def ask[F[_], A](implicit F: Applicative[F]): Kleisli[F, A, A] =
    Kleisli(F.pure)

  def local[M[_], A, R](f: R => R)(fa: Kleisli[M, R, A]): Kleisli[M, R, A] =
    Kleisli(f andThen fa.run)
}

We can use the Kleisli() constructor to construct a Kliesli value:

import cats._, cats.data._, cats.syntax.all._

val f = Kleisli { (x: Int) => (x + 1).some }
// f: Kleisli[Option, Int, Int] = Kleisli(run = <function1>)

val g = Kleisli { (x: Int) => (x * 100).some }
// g: Kleisli[Option, Int, Int] = Kleisli(run = <function1>)

We can then compose the functions using compose, which runs the right-hand side first:

4.some >>= (f compose g).run
// res0: Option[Int] = Some(value = 401)

There’s also andThen, which runs the left-hand side first:

4.some >>= (f andThen g).run
// res1: Option[Int] = Some(value = 500)

Both compose and andThen work like function composition but note that they retain the monadic context.

lift method 

Kleisli also has some interesting methods like lift, which allows you to lift a monadic function into another applicative functor. When I tried using it, I realized it’s broken, so here’s the fixed version #354:

  def lift[G[_]](implicit G: Applicative[G]): Kleisli[λ[α => G[F[α]]], A, B] =
    Kleisli[λ[α => G[F[α]]], A, B](a => Applicative[G].pure(run(a)))

Here’s how we can use it:

{
  val l = f.lift[List]

  List(1, 2, 3) >>= l.run
}
// res2: List[Option[Int]] = List(
//   Some(value = 2),
//   Some(value = 3),
//   Some(value = 4)
// )

Making monads 

LYAHFGG:

In this section, we’re going to look at an example of how a type gets made, identified as a monad and then given the appropriate Monad instance. … What if we wanted to model a non-deterministic value like [3,5,9], but we wanted to express that 3 has a 50% chance of happening and 5 and 9 both have a 25% chance of happening?

Since Scala doesn’t have a built-in rational, let’s just use Double. Here’s the case class:

import cats._, cats.syntax.all._

case class Prob[A](list: List[(A, Double)])

trait ProbInstances {
  implicit def probShow[A]: Show[Prob[A]] = Show.fromToString
}

case object Prob extends ProbInstances

Is this a functor? Well, the list is a functor, so this should probably be a functor as well, because we just added some stuff to the list.

case class Prob[A](list: List[(A, Double)])

trait ProbInstances {
  implicit val probInstance: Functor[Prob] = new Functor[Prob] {
    def map[A, B](fa: Prob[A])(f: A => B): Prob[B] =
      Prob(fa.list map { case (x, p) => (f(x), p) })
  }
  implicit def probShow[A]: Show[Prob[A]] = Show.fromToString
}

case object Prob extends ProbInstances

Prob((3, 0.5) :: (5, 0.25) :: (9, 0.25) :: Nil) map { -_ }
// res1: Prob[Int] = Prob(list = List((-3, 0.5), (-5, 0.25), (-9, 0.25)))

Just like the book, we are going to implement flatten first.

case class Prob[A](list: List[(A, Double)])

trait ProbInstances {
  def flatten[B](xs: Prob[Prob[B]]): Prob[B] = {
    def multall(innerxs: Prob[B], p: Double) =
      innerxs.list map { case (x, r) => (x, p * r) }
    Prob((xs.list map { case (innerxs, p) => multall(innerxs, p) }).flatten)
  }

  implicit val probInstance: Functor[Prob] = new Functor[Prob] {
    def map[A, B](fa: Prob[A])(f: A => B): Prob[B] =
      Prob(fa.list map { case (x, p) => (f(x), p) })
  }
  implicit def probShow[A]: Show[Prob[A]] = Show.fromToString
}

case object Prob extends ProbInstances

This should be enough prep work for monad:

import scala.annotation.tailrec

case class Prob[A](list: List[(A, Double)])

trait ProbInstances { self =>
  def flatten[B](xs: Prob[Prob[B]]): Prob[B] = {
    def multall(innerxs: Prob[B], p: Double) =
      innerxs.list map { case (x, r) => (x, p * r) }
    Prob((xs.list map { case (innerxs, p) => multall(innerxs, p) }).flatten)
  }

  implicit val probInstance: Monad[Prob] = new Monad[Prob] {

    def pure[A](a: A): Prob[A] = Prob((a, 1.0) :: Nil)

    def flatMap[A, B](fa: Prob[A])(f: A => Prob[B]): Prob[B] = self.flatten(map(fa)(f))

    override def map[A, B](fa: Prob[A])(f: A => B): Prob[B] =
      Prob(fa.list map { case (x, p) => (f(x), p) })

    def tailRecM[A, B](a: A)(f: A => Prob[Either[A, B]]): Prob[B] = {
      val buf = List.newBuilder[(B, Double)]

      @tailrec def go(lists: List[List[(Either[A, B], Double)]]): Unit =
        lists match {
          case (ab :: abs) :: tail => ab match {
            case (Right(b), p) =>
              buf += ((b, p))
              go(abs :: tail)
            case (Left(a), p) =>
              go(f(a).list :: abs :: tail)
          }
          case Nil :: tail => go(tail)
          case Nil => ()
        }
      go(f(a).list :: Nil)
      Prob(buf.result)
    }
  }

  implicit def probShow[A]: Show[Prob[A]] = Show.fromToString
}

case object Prob extends ProbInstances

The book says it satisfies the monad laws. Let’s implement the Coin example:

sealed trait Coin

object Coin {
  case object Heads extends Coin
  case object Tails extends Coin
  implicit val coinEq: Eq[Coin] = new Eq[Coin] {
    def eqv(a1: Coin, a2: Coin): Boolean = a1 == a2
  }
  def heads: Coin = Heads
  def tails: Coin = Tails
}

import Coin.{heads, tails}

def coin: Prob[Coin] = Prob(heads -> 0.5 :: tails -> 0.5 :: Nil)

def loadedCoin: Prob[Coin] = Prob(heads -> 0.1 :: tails -> 0.9 :: Nil)

Here’s how we can implement flipThree:

def flipThree: Prob[Boolean] = for {
  a <- coin
  b <- coin
  c <- loadedCoin
} yield { List(a, b, c) forall {_ === tails} }

flipThree
// res4: Prob[Boolean] = Prob(
//   list = List(
//     (false, 0.025),
//     (false, 0.225),
//     (false, 0.025),
//     (false, 0.225),
//     (false, 0.025),
//     (false, 0.225),
//     (false, 0.025),
//     (true, 0.225)
//   )
// )

So the probability of having all three coins on Tails even with a loaded coin is pretty low.

Monads are fractals 

The intuition for FlatMap and Monad we built on day 5 via the tightrope walking example is that a monadic chaining >>= can carry context from one operation to the next. A single None in an intermediate value banishes the entire chain.

The context monad instances carry along is different. The State datatype we saw on day 7 for example automates the explicit passing of the state object with >>=.

This is a useful intuition of monads to have in comparison to Functor, Apply, and Applicative, but it doesn’t tell the whole story.

Another intuition about monads (technically FlatMap) is that they are fractals, like the above Sierpinski triangle. Each part of a fractal is self-similar to the whole shape.

Take List for example. A List of Lists can be treated a flat List.

val xss = List(List(1), List(2, 3), List(4))
// xss: List[List[Int]] = List(List(1), List(2, 3), List(4))

xss.flatten
// res0: List[Int] = List(1, 2, 3, 4)

The flatten function embodies the crunching of the List data structure. If we think in terms of the type signature, it would be F[F[A]] => F[A].

List forms a monad under ++ 

We can get a better idea of the flattening by reimplementing it using foldLeft:

xss.foldLeft(List(): List[Int]) { _ ++ _ }
// res1: List[Int] = List(1, 2, 3, 4)

We can say that List forms a monad under ++.

Option forms a monad under? 

Now let try to figure out under what operation does Option form a monad:

val o1 = Some(None: Option[Int]): Option[Option[Int]]
// o1: Option[Option[Int]] = Some(value = None)

val o2 = Some(Some(1): Option[Int]): Option[Option[Int]]
// o2: Option[Option[Int]] = Some(value = Some(value = 1))

val o3 = None: Option[Option[Int]]
// o3: Option[Option[Int]] = None

And here’s the foldLeft:

o1.foldLeft(None: Option[Int]) { (_, _)._2 }
// res2: Option[Int] = None

o2.foldLeft(None: Option[Int]) { (_, _)._2 }
// res3: Option[Int] = Some(value = 1)

o3.foldLeft(None: Option[Int]) { (_, _)._2 }
// res4: Option[Int] = None

It seems like Option forms a monad under (_, _)._2.

State as a fractal 

If we come back to the State datatype from the point of view of fractals, it becomes clear that a State of State is also a State. This property allows us to create mini-programs like pop and push, and compose them into a larger State using for comprehension:

def stackManip: State[Stack, Int] = for {
  _ <- push(3)
  a <- pop
  b <- pop
} yield(b)

We also saw similar composition with the Free monad.

In short, monadic values compose within the same monad instance.

Look out for fractals 

When you want to find your own monad, keep a lookout for the fractal structure. From there, see if you can implement the flatten function F[F[A]] => F[A].

day 10 

On day 9 we reviewed monadic functions flatten, filterM, and the implementation of foldM. Next we made a safe RPN calculator using foldM, looked at Kleisli composition, implemented our own monad Prob, and thought about fractals.

Since Cats does not provide Zippers, we are now done with Learn You a Haskell for Great Good, and we need to find our own topic.

One topic we have been dancing around, but haven’t gotten into is the notion of the monad transformer. Luckily there’s another good Haskell book that I’ve read that’s also available online.

Monad transformers 

Real World Haskell says:

It would be ideal if we could somehow take the standard State monad and add failure handling to it, without resorting to the wholesale construction of custom monads by hand. The standard monads in the mtl library don’t allow us to combine them. Instead, the library provides a set of monad transformers to achieve the same result.

A monad transformer is similar to a regular monad, but it’s not a standalone entity: instead, it modifies the behaviour of an underlying monad.

Dependency injection again 

Let’s look into the idea of using Reader datatype (Function1) for dependency injection, which we saw on day 6.

case class User(id: Long, parentId: Long, name: String, email: String)

trait UserRepo {
  def get(id: Long): User
  def find(name: String): User
}

Jason Arhart’s Scrap Your Cake Pattern Boilerplate: Dependency Injection Using the Reader Monad generalizes the notion of Reader datatype for supporting multiple services by creating a Config object:

import java.net.URI

trait HttpService {
  def get(uri: URI): String
}

trait Config {
  def userRepo: UserRepo
  def httpService: HttpService
}

To use this, we would construct mini-programs of type Config => A, and compose them.

Suppose we want to also encode the notion of failure using Option.

Kleisli as ReaderT 

We can use the Kleisli datatype we saw yesterday as ReaderT, a monad transformer version of the Reader datatype, and stack it on top of Option like this:

import cats._, cats.data._, cats.syntax.all._

type ReaderTOption[A, B] = Kleisli[Option, A, B]

object ReaderTOption {
  def ro[A, B](f: A => Option[B]): ReaderTOption[A, B] = Kleisli(f)
}

We can modify the Config to make httpService optional:

import java.net.URI

case class User(id: Long, parentId: Long, name: String, email: String)

trait UserRepo {
  def get(id: Long): Option[User]
  def find(name: String): Option[User]
}

trait HttpService {
  def get(uri: URI): String
}

trait Config {
  def userRepo: UserRepo
  def httpService: Option[HttpService]
}

Next we can rewrite the “primitive” readers to return ReaderTOption[Config, A]:

trait Users {
  def getUser(id: Long): ReaderTOption[Config, User] =
    ReaderTOption.ro {
      case config => config.userRepo.get(id)
    }

  def findUser(name: String): ReaderTOption[Config, User] =
    ReaderTOption.ro {
      case config => config.userRepo.find(name)
    }
}

trait Https {
  def getHttp(uri: URI): ReaderTOption[Config, String] =
    ReaderTOption.ro {
      case config => config.httpService map {_.get(uri)}
    }
}

We can compose these mini-programs into compound programs:

trait Program extends Users with Https {
  def userSearch(id: Long): ReaderTOption[Config, String] =
    for {
      u <- getUser(id)
      r <- getHttp(new URI("http://www.google.com/?q=" + u.name))
    } yield r
}

object Main extends Program {
  def run(config: Config): Option[String] =
    userSearch(2).run(config)
}

val dummyConfig: Config = new Config {
  val testUsers = List(User(0, 0, "Vito", "vito@example.com"),
    User(1, 0, "Michael", "michael@example.com"),
    User(2, 0, "Fredo", "fredo@example.com"))

  def userRepo: UserRepo = new UserRepo {
    def get(id: Long): Option[User] =
      testUsers find { _.id === id }
    def find(name: String): Option[User] =
      testUsers find { _.name === name }
  }

  def httpService: Option[HttpService] = None
}
// dummyConfig: Config = repl.MdocSession1@659c61d9

The above ReaderTOption datatype combines Reader’s ability to read from some configuration once, and the Option’s ability to express failure.

Stacking multiple monad transformers 

RWH:

When we stack a monad transformer on a normal monad, the result is another monad. This suggests the possibility that we can again stack a monad transformer on top of our combined monad, to give a new monad, and in fact this is a common thing to do.

We can stack StateT on top of ReaderTOption to represent state transfer.

type StateTReaderTOption[C, S, A] = StateT[({type l[X] = ReaderTOption[C, X]})#l, S, A]

object StateTReaderTOption {
  def state[C, S, A](f: S => (S, A)): StateTReaderTOption[C, S, A] =
    StateT[({type l[X] = ReaderTOption[C, X]})#l, S, A] {
      s: S => Monad[({type l[X] = ReaderTOption[C, X]})#l].pure(f(s))
    }

  def get[C, S]: StateTReaderTOption[C, S, S] =
    state { s => (s, s) }

  def put[C, S](s: S): StateTReaderTOption[C, S, Unit] =
    state { _ => (s, ()) }

  def ro[C, S, A](f: C => Option[A]): StateTReaderTOption[C, S, A] =
    StateT[({type l[X] = ReaderTOption[C, X]})#l, S, A] {
      s: S =>
        ReaderTOption.ro[C, (S, A)]{
          c: C => f(c) map {(s, _)}
        }
    }
}

This is a bit confusing, so let’s break it down. Ultimately the point of State datatype is to wrap S => (S, A), so I kept those parameter names for state. Next, I needed to modify the kind of ReaderTOption to * -> * (a type constructor that takes exactly one type as its parameter).

Similarly, we need a way of using this datatype as a ReaderTOption, which is expressed as C => Option[A] in ro.

We also can implement a Stack again. This time let’s use String instead.

type Stack = List[String]

{
  val pop = StateTReaderTOption.state[Config, Stack, String] {
    case x :: xs => (xs, x)
    case _       => ???
  }
}

Here’s a version of pop and push using get and put primitive:

import StateTReaderTOption.{get, put}

val pop: StateTReaderTOption[Config, Stack, String] =
  for {
    s <- get[Config, Stack]
    (x :: xs) = s
    _ <- put(xs)
  } yield x
// pop: StateTReaderTOption[Config, Stack, String] = cats.data.IndexedStateT@136ad671

def push(x: String): StateTReaderTOption[Config, Stack, Unit] =
  for {
    xs <- get[Config, Stack]
    r <- put(x :: xs)
  } yield r

We can also port stackManip:

def stackManip: StateTReaderTOption[Config, Stack, String] =
  for {
    _ <- push("Fredo")
    a <- pop
    b <- pop
  } yield(b)

Here’s how we can use this:

stackManip.run(List("Hyman Roth")).run(dummyConfig)
// res3: Option[(Stack, String)] = Some(value = (List(), "Hyman Roth"))

So far we have the same feature as the State version. We can modify Users to use StateTReaderTOption.ro:

trait Users {
  def getUser[S](id: Long): StateTReaderTOption[Config, S, User] =
    StateTReaderTOption.ro[Config, S, User] {
      case config => config.userRepo.get(id)
    }

  def findUser[S](name: String): StateTReaderTOption[Config, S, User] =
    StateTReaderTOption.ro[Config, S, User] {
      case config => config.userRepo.find(name)
    }
}

Using this we can now manipulate the stack using the read-only configuration:

trait Program extends Users {
  def stackManip: StateTReaderTOption[Config, Stack, Unit] =
    for {
      u <- getUser(2)
      a <- push(u.name)
    } yield(a)
}

object Main extends Program {
  def run(s: Stack, config: Config): Option[(Stack, Unit)] =
    stackManip.run(s).run(config)
}

We can run this program like this:

Main.run(List("Hyman Roth"), dummyConfig)
// res4: Option[(Stack, Unit)] = Some(
//   value = (List("Fredo", "Hyman Roth"), ())
// )

Now we have StateT, ReaderT and Option working all at the same time. Maybe I am not doing it right, but setting up the monad constructor functions like state and ro to set up StateTReaderTOption is a rather mind-bending excercise.

Once the primitive monadic values are constructed, the usage code (like stackManip) looks relatively clean. It sure does avoid the cake pattern, but the stacked monad type StateTReaderTOption is sprinkled all over the code base.

If all we wanted was being able to use getUser(id: Long) and push etc., an alternative is to construct a DSL with those commands using Free monads we saw on day 8.

Stacking Future and Either 

One use of monad transformers that seem to come up often is stacking Future datatype with Either. There’s a blog post by Yoshida-san (@xuwei_k) in Japanese called How to combine Future and Either nicely in Scala.

A little known fact about Yoshida-san outside of Tokyo, is that he majored in Chinese calligraphy. Apparently he spent his college days writing ancient seal scripts and carving seals:

「大学では、はんこを刻ったり、篆書を書いてました」 「えっ？なぜプログラマに？？？」 pic.twitter.com/DEhqy4ELpF

— Kenji Yoshida (@xuwei_k) October 21, 2013

His namesake Xu Wei was a Ming-era painter, poet, writer and dramatist famed for his free-flowing style. Here’s Yoshida-san writing functional programming language.

In any case, why would one want to stack Future and Either together? The blog post explains like this:

1. Future[A] comes up a lot in Scala.
2. You don’t want to block future, so you end up with Future everywhere.
3. Since Future is asynchronous, any errors need to be captured in there.
4. Future is designed to handle Throwable, but that’s all you get.
5. When the program becomes complex enough, you want to type your own error states.
6. How can we make Future of Either?

Here’s the prepration step:

case class User(id: Long, name: String)

// In actual code, probably more than 2 errors
sealed trait Error

object Error {
  final case class UserNotFound(userId: Long) extends Error
  final case class ConnectionError(message: String) extends Error
}

object UserRepo {
  def followers(userId: Long): Either[Error, List[User]] = ???
}

import UserRepo.followers

Suppose our application allows the users to follow each other like Twitter. The followers function returns the list of followers.

Now let’s try writing a function that checks if two users follow each other.

def isFriends0(user1: Long, user2: Long): Either[Error, Boolean] =
  for {
    a <- followers(user1).right
    b <- followers(user2).right
  } yield a.exists(_.id == user2) && b.exists(_.id == user1)

Now suppose we want to make the database access async so we changed the followers to return a Future like this:

import scala.concurrent.{ Future, ExecutionContext }
object UserRepo {
  def followers(userId: Long): Future[Either[Error, List[User]]] = ???
}
import UserRepo.followers

Now, how would isFriends0 look like? Here’s one way of writing this:

def isFriends1(user1: Long, user2: Long)
  (implicit ec: ExecutionContext): Future[Either[Error, Boolean]] =
  for {
    a <- followers(user1)
    b <- followers(user2)
  } yield for {
    x <- a.right
    y <- b.right
  } yield x.exists(_.id == user2) && y.exists(_.id == user1)

And here’s another version:

def isFriends2(user1: Long, user2: Long)
  (implicit ec: ExecutionContext): Future[Either[Error, Boolean]] =
  followers(user1) flatMap {
    case Right(a) =>
      followers(user2) map {
        case Right(b) =>
          Right(a.exists(_.id == user2) && b.exists(_.id == user1))
        case Left(e) =>
          Left(e)
      }
    case Left(e) =>
      Future.successful(Left(e))
  }

What is the difference between the two versions? They’ll both behave the same if followers return normally, but suppose followers(user1) returns an Error state. isFriend1 would still call followers(user2), whereas isFriend2 would short-circuit and return the error.

Regardless, both functions became convoluted compared to the original. And it’s mostly a boilerplate to satisfy the types. I don’t want to imagine doing this for every function that uses Future[Either[Error, A]].

EitherT datatype 

Cats comes with EitherT datatype, which is a monad transformer for Either.

/**
 * Transformer for `Either`, allowing the effect of an arbitrary type constructor `F` to be combined with the
 * fail-fast effect of `Either`.
 *
 * `EitherT[F, A, B]` wraps a value of type `F[Either[A, B]]`. An `F[C]` can be lifted in to `EitherT[F, A, C]` via `EitherT.right`,
 * and lifted in to a `EitherT[F, C, B]` via `EitherT.left`.
 */
case class EitherT[F[_], A, B](value: F[Either[A, B]]) {
  ....
}

Here’s UserRepo.followers with a dummy implementation:

import cats._, cats.data._, cats.syntax.all._

object UserRepo {
  def followers(userId: Long)
    (implicit ec: ExecutionContext): EitherT[Future, Error, List[User]] =
    userId match {
      case 0L =>
        EitherT.right(Future { List(User(1, "Michael")) })
      case 1L =>
        EitherT.right(Future { List(User(0, "Vito")) })
      case x =>
        println("not found")
        EitherT.left(Future.successful { Error.UserNotFound(x) })
    }
}
import UserRepo.followers

Now let’s try writing isFriends0 function again.

def isFriends3(user1: Long, user2: Long)
  (implicit ec: ExecutionContext): EitherT[Future, Error, Boolean] =
  for{
    a <- followers(user1)
    b <- followers(user2)
  } yield a.exists(_.id == user2) && b.exists(_.id == user1)

Isn’t this great? Except for the type signature and the ExecutionContext, isFriends3 is identical to isFriends0.

Now let’s try using this.

{
  implicit val ec = scala.concurrent.ExecutionContext.global
  import scala.concurrent.Await
  import scala.concurrent.duration._

  Await.result(isFriends3(0, 1).value, 1 second)
}
// res2: Either[Error, Boolean] = Right(value = true)

When the first user is not found, EitherT will short circuit.

{
  implicit val ec = scala.concurrent.ExecutionContext.global
  import scala.concurrent.Await
  import scala.concurrent.duration._

  Await.result(isFriends3(2, 3).value, 1 second)
}
// not found
// res3: Either[Error, Boolean] = Left(value = UserNotFound(userId = 2L))

Note that "not found" is printed only once.

Unlike the StateTReaderTOption example, EitherT seems usable in many situations.

That’s it for today!

day 11 

On day 10 we looked at the idea of monad transformers, first using Kliesli as ReaderT, and also stacking Future and Either.

Genericity 

In the grand scheme of things, functional programming is about abstracting things out. Skimming over Jeremy Gibbons’s 2006 book Datatype-Generic Programming, I found a nice overview.

Generic programming is about making programming languages more flexible without compromising safety.

Genericity by value 

One of the first and most fundamental techniques that any programmer learns is how to parametrize computations by values

def triangle4: Unit = {
  println("*")
  println("**")
  println("***")
  println("****")
}

We can abstract out 4 into a parameter:

def triangle(side: Int): Unit = {
  (1 to side) foreach { row =>
    (1 to row) foreach { col =>
      println("*")
    }
  }
}

Genericity by type 

List[A] is a polymorphic datatype parametrized by another type, the type of list elements. This enables parametric polymorphism.

def head[A](xs: List[A]): A = xs(0)

The above function would work for all proper types.

Genericity by function 

Higher-order programs are programs parametrized by other programs.

For example foldLeft can be used to append two lists:

def append[A](list: List[A], ys: List[A]): List[A] =
  list.foldLeft(ys) { (acc, x) => x :: acc }

append(List(1, 2, 3), List(4, 5, 6))
// res0: List[Int] = List(3, 2, 1, 4, 5, 6)

Or it can also be used to add numbers:

def sum(list: List[Int]): Int =
 list.foldLeft(0) { _ + _ }

Genericity by structure 

“Generic programming” embodied in the sense of a collection library, like Scala Collections. In the case of C++’s Standard Template Library, the parametric datatypes are called containers, and various abstractions are provided via iterators, such as input iterators and forward iterators.

The notion of the typeclass fits in here too.

trait Read[A] {
  def reads(s: String): Option[A]
}

object Read extends ReadInstances {
  def read[A](f: String => Option[A]): Read[A] = new Read[A] {
    def reads(s: String): Option[A] = f(s)
  }
  def apply[A: Read]: Read[A] = implicitly[Read[A]]
}

trait ReadInstances {
  implicit lazy val stringRead: Read[String] =
    Read.read[String] { Some(_) }
  implicit lazy val intRead: Read[Int] =
    Read.read[Int] { s =>
      try {
        Some(s.toInt)
      } catch {
        case e: NumberFormatException => None
      }
    }
}

Read[Int].reads("1")
// res1: Option[Int] = Some(value = 1)

The typeclass captures the requirements required of types, called typeclass contract. It also lets us list the types providing these requirements by defining typeclass instances. This enables ad-hoc polymorphism because A in Read[A] is not universal.

Genericity by property 

In Scala Collection library, some of the concepts promised are more elaborate than the list of operations covered by the type.

as well as signatures of operations, the concept might specify the laws these operations satisfy, and non-functional characteristics such as the asymptotic complexities of the operations in terms of time and space.

Typeclasses with laws fit in here too. For example Monoid[A] comes with the monoid laws. The laws need to be validated for each instance using property-based testing tools.

Genericity by stage 

Various flavors of metaprogramming can be though of as the development or program that construct or manipulate other programs. This could include code generation and macros.

Genericity by shape 

Let’s say there’s a polymorphic datatype of binary trees:

sealed trait Btree[A]
object Btree {
  case class Tip[A](a: A) extends Btree[A]
  case class Bin[A](left: Btree[A], right: Btree[A]) extends Btree[A]
}

Let’s write foldB as a way of abstracting similar programs.

def foldB[A, B](tree: Btree[A], b: (B, B) => B)(t: A => B): B =
  tree match {
    case Btree.Tip(a)      => t(a)
    case Btree.Bin(xs, ys) => b(foldB(xs, b)(t), foldB(ys, b)(t))
  }

The next goal is to abstract foldB and foldLeft.

In fact, what differs between the two fold operators is the shape of the data on which they operate, and hence the shape of the programs themselves. The kind of parametrization required is by this shape; that is, by the datatype or type constructor (such as List or Tree) concerned. We call this datatype genericity.

For example, fold apparently could be expressed as

import cats._, cats.data._, cats.syntax.all._

trait Fix[F[_,_], A]
def cata[S[_,_]: Bifunctor, A, B](t: Fix[S, A])(f: S[A, B] => B): B = ???

In the above, S represents the shape of the datatype. By abstracting out the shapes, we can construct parametrically datatype-generic programs. We’ll come back to this later.

Alternatively, such programs might be ad-hoc datatype-generic, when the behaviour exploits that shape in some essential manner. Typical examples of the latter are pretty printers and marshallers.

The example that fits in this category might be Scala Pickling. Pickling defines picklers for common types, and it derives pickler instances for different shapes using macro.

This approach to datatype genericity has been variously called polytypism, structural polymorphism or typecase , and is the meaning given to ‘generic programming’ by the Generic Haskell team. Whatever the name, functions are defined inductively by case analysis on the structure of datatypes ….

We consider parametric datatype genericity to be the ‘gold standard’, and in the remainder of these lecture notes, we concentrate on parametric datatype-generic definitions where possible.

In Scala, shapeless is focused on abstracting out the shape.

Datatype-generic programming with Bifunctor 

Moving on the section 3.6 in Datatype-Generic Programming called “Datatype genericity.” Gibbons tries to call this Origami programming, but I don’t think the name stuck, so we’ll go with datatype-generic programming.

As we have already argued, data structure determines program structure. It therefore makes sense to abstract from the determining shape, leaving only what programs of different shape have in common. What datatypes such as List and Tree have in common is the fact that they are recursive — which is to say, a datatype Fix

data Fix s a = In {out :: s a (Fix s a)}

Here are three instances of Fix using different shapes: lists and internally labelled binary trees as seen before, and also a datatype of externally labelled binary trees.

data ListF a b = NilF | ConsF a b
type List a = Fix ListF a
data TreeF a b = EmptyF | NodeF a b b
type Tree a = Fix TreeF a
data BtreeF a b = TipF a | BinF b b
type Btree a = Fix BtreeF a

From Why free monads matter we saw on day 8 we actually know this is similar as Free datatype, but the semantics around Functor etc is going to different, so let’s implement it from scratch:

sealed abstract class Fix[S[_], A] extends Serializable {
  def out: S[Fix[S, A]]
}

object Fix {
  case class In[S[_], A](out: S[Fix[S, A]]) extends Fix[S, A]
}

Following Free, I am putting S[_] on the left, and A on the right.

Let’s try implementing the List first.

sealed trait ListF[+Next, +A]

object ListF {
  case class NilF() extends ListF[Nothing, Nothing]
  case class ConsF[A, Next](a: A, n: Next) extends ListF[Next, A]
}

type GenericList[A] = Fix[ListF[+*, A], A]

object GenericList {
  def nil[A]: GenericList[A] = Fix.In[ListF[+*, A], A](ListF.NilF())
  def cons[A](a: A, xs: GenericList[A]): GenericList[A] =
    Fix.In[ListF[+*, A], A](ListF.ConsF(a, xs))
}

import GenericList.{ cons, nil }

Here’s how we can use it:

cons(1, nil)
// res0: GenericList[Int] = In(out = ConsF(a = 1, n = In(out = NilF())))

So far this is similar to what we saw with the free monad.

Bifunctor 

Not all valid binary type constructors s are suitable for Fixing; for example, function types with the parameter appearing in contravariant (source) positions cause problems. It turns out that we should restrict attention to (covariant) bifunctors, which support a bimap operation ‘locating’ all the elements.

Cats ships with Bifunctor:

/**
 * A typeclass of types which give rise to two independent, covariant
 * functors.
 */
trait Bifunctor[F[_, _]] extends Serializable { self =>

  /**
   * The quintessential method of the Bifunctor trait, it applies a
   * function to each "side" of the bifunctor.
   */
  def bimap[A, B, C, D](fab: F[A, B])(f: A => C, g: B => D): F[C, D]

  ....
}

Here is the Bifunctor instance for GenericList.

import cats._, cats.data._, cats.syntax.all._

implicit val listFBifunctor: Bifunctor[ListF] = new Bifunctor[ListF] {
  def bimap[S1, A1, S2, A2](fab: ListF[S1, A1])(f: S1 => S2, g: A1 => A2): ListF[S2, A2] =
    fab match {
      case ListF.NilF()         => ListF.NilF()
      case ListF.ConsF(a, next) => ListF.ConsF(g(a), f(next))
    }
}
// listFBifunctor: Bifunctor[ListF] = repl.MdocSession1@1f266bef

Deriving map from Bifunctor 

It turns out that the class Bifunctor provides sufficient flexibility to capture a wide variety of recursion patterns as datatype-generic programs.

First, we can implement map in terms of bimap.

object DGP {
  def map[F[_, _]: Bifunctor, A1, A2](fa: Fix[F[*, A1], A1])(f: A1 => A2): Fix[F[*, A2], A2] =
    Fix.In[F[*, A2], A2](Bifunctor[F].bimap(fa.out)(map(_)(f), f))
}

DGP.map(cons(1, nil)) { _ + 1 }
// res1: Fix[ListF[α4, Int], Int] = In(
//   out = ConsF(a = 2, n = In(out = NilF()))
// )

The above definition of map is independent from GenericList, abstracted by Bifunctor and Fix. Another way of looking at it is that we can get Functor for free out of Bifunctor and Fix.

trait FixInstances {
  implicit def fixFunctor[F[_, _]: Bifunctor]: Functor[Lambda[L => Fix[F[*, L], L]]] =
    new Functor[Lambda[L => Fix[F[*, L], L]]] {
      def map[A1, A2](fa: Fix[F[*, A1], A1])(f: A1 => A2): Fix[F[*, A2], A2] =
        Fix.In[F[*, A2], A2](Bifunctor[F].bimap(fa.out)(map(_)(f), f))
    }
}

{
  val instances = new FixInstances {}
  import instances._
  import cats.syntax.functor._
  cons(1, nil) map { _ + 1 }
}
// res2: GenericList[Int] = In(out = ConsF(a = 2, n = In(out = NilF())))

Intense amount of type lambdas, but I think it’s clear that I translated DB.map into a Functor instance.

Deriving fold from Bifunctor 

We can also implement fold, also known as cata from catamorphism:

object DGP {
  // catamorphism
  def fold[F[_, _]: Bifunctor, A1, A2](fa: Fix[F[*, A1], A1])(f: F[A2, A1] => A2): A2 =
    {
      val g = (fa1: F[Fix[F[*, A1], A1], A1]) =>
        Bifunctor[F].leftMap(fa1) { (fold(_)(f)) }
      f(g(fa.out))
    }
}

DGP.fold[ListF, Int, Int](cons(2, cons(1, nil))) {
  case ListF.NilF()      => 0
  case ListF.ConsF(x, n) => x + n
}
// res4: Int = 3

Deriving unfold from Bifunctor 

The unfold operator for a datatype grows a data structure from a value. In a precise technical sense, it is the dual of the fold operator.

The unfold is also called ana from anamorphism:

object DGP {
  // catamorphism
  def fold[F[_, _]: Bifunctor, A1, A2](fa: Fix[F[*, A1], A1])(f: F[A2, A1] => A2): A2 =
    {
      val g = (fa1: F[Fix[F[*, A1], A1], A1]) =>
        Bifunctor[F].leftMap(fa1) { (fold(_)(f)) }
      f(g(fa.out))
    }

  // anamorphism
  def unfold[F[_, _]: Bifunctor, A1, A2](x: A2)(f: A2 => F[A2, A1]): Fix[F[*, A1], A1] =
    Fix.In[F[*, A1], A1](Bifunctor[F].leftMap(f(x))(unfold[F, A1, A2](_)(f)))
}

Here’s how we can construct list of numbers counting down:

def pred(n: Int): GenericList[Int] =
  DGP.unfold[ListF, Int, Int](n) {
    case 0 => ListF.NilF()
    case n => ListF.ConsF(n, n - 1)
  }

pred(4)
// res6: GenericList[Int] = In(
//   out = ConsF(
//     a = 4,
//     n = In(
//       out = ConsF(
//         a = 3,
//         n = In(
//           out = ConsF(a = 2, n = In(out = ConsF(a = 1, n = In(out = NilF()))))
//         )
//       )
//     )
//   )
// )

There are several more we can derive, too.

Tree 

The point of the datatype-generic programming is to abstract out the shape. Let’s introduce some other datatype, like a binary Tree:

sealed trait TreeF[+Next, +A]
object TreeF {
  case class EmptyF() extends TreeF[Nothing, Nothing]
  case class NodeF[Next, A](a: A, left: Next, right: Next) extends TreeF[Next, A]
}

type Tree[A] = Fix[TreeF[?, A], A]
object Tree {
  def empty[A]: Tree[A] =
    Fix.In[TreeF[+?, A], A](TreeF.EmptyF())
  def node[A, Next](a: A, left: Tree[A], right: Tree[A]): Tree[A] =
    Fix.In[TreeF[+?, A], A](TreeF.NodeF(a, left, right))
}

Here’s how to create this tree:

import Tree.{empty,node}
node(2, node(1, empty, empty), empty)
// res7: Tree[Int] = In(
//   out = NodeF(
//     a = 2,
//     left = In(
//       out = NodeF(a = 1, left = In(out = EmptyF()), right = In(out = EmptyF()))
//     ),
//     right = In(out = EmptyF())
//   )
// )

Now, all we have to do should be to define a Bifunctor instance:

implicit val treeFBifunctor: Bifunctor[TreeF] = new Bifunctor[TreeF] {
  def bimap[A, B, C, D](fab: TreeF[A, B])(f: A => C, g: B => D): TreeF[C, D] =
    fab match {
      case TreeF.EmptyF() => TreeF.EmptyF()
      case TreeF.NodeF(a, left, right) =>
        TreeF.NodeF(g(a), f(left), f(right))
    }
}
// treeFBifunctor: Bifunctor[TreeF] = repl.MdocSession7@6542baa6

First, let’s try Functor:

{
  val instances = new FixInstances {}
  import instances._
  import cats.syntax.functor._
  node(2, node(1, empty, empty), empty) map { _ + 1 }
}
// res8: Tree[Int] = In(
//   out = NodeF(
//     a = 3,
//     left = In(
//       out = NodeF(a = 2, left = In(out = EmptyF()), right = In(out = EmptyF()))
//     ),
//     right = In(out = EmptyF())
//   )
// )

Looking good. Next, let’s try folding.

def sum(tree: Tree[Int]): Int =
  DGP.fold[TreeF, Int, Int](tree) {
    case TreeF.EmptyF()       => 0
    case TreeF.NodeF(a, l, r) => a + l + r
  }

sum(node(2, node(1, empty, empty), empty))
// res9: Int = 3

We got the fold.

Here’s a function named grow that generates a binary search tree from a list.

def grow[A: PartialOrder](xs: List[A]): Tree[A] =
   DGP.unfold[TreeF, A, List[A]](xs) {
     case Nil => TreeF.EmptyF()
     case x :: xs =>
       import cats.syntax.partialOrder._
       TreeF.NodeF(x, xs filter {_ <= x}, xs filter {_ > x})
   }

grow(List(3, 1, 4, 2))
// res10: Tree[Int] = In(
//   out = NodeF(
//     a = 3,
//     left = In(
//       out = NodeF(
//         a = 1,
//         left = In(out = EmptyF()),
//         right = In(
//           out = NodeF(
//             a = 2,
//             left = In(out = EmptyF()),
//             right = In(out = EmptyF())
//           )
//         )
//       )
//     ),
//     right = In(
//       out = NodeF(a = 4, left = In(out = EmptyF()), right = In(out = EmptyF()))
//     )
//   )
// )

Looks like unfold is working too.

For more details on DGP in Scala, Oliveira and Gibbons wrote a paper translating the ideas and many more called Scala for Generic Programmers (2008), and its updated version Scala for Generic Programmers (2010).

Datatype-generic programming described here has a limitation of datatype being recursive, so I don’t think it’s very usable as is, but there are some interesting concepts that can be exploited.

The Origami patterns 

Next, Gibbons claims that the design patterns are evidence of a “evidence of a lack of expressivity in those mainstream programming languages.” He then sets out to replace the patterns using higher-order datatype-generic programming.

Const datatype 

Chapter 5 of Datatype-Generic Programming, the last one before Conclusions, is called “The Essence of the Iterator pattern,” the same name of the paper Gibbons and Oliveira wrote in 2006. The one available online as The Essence of the Iterator Pattern is from 2009. Reading this paper as a continuation of DGP gives it a better context.

Here’s the example given at the beginning of this paper, translated to Java.

public static <E> int loop(Collection<E> coll) {
  int n = 0;
  for (E elem: coll) {
    n = n + 1;
    doSomething(elem);
  }
  return n;
}

EIP:

We emphasize that we want to capture both aspects of the method loop and iterations like it: mapping over the elements, and simultaneously accumulating some measure of those elements.

The first half of the paper reviews functional iterations and applicative style. For applicative functors, it brings up the fact that there are three kinds of applicatives:

1. Monadic applicative functors
2. Naperian applicative functors
3. Monoidal applicative functors

We’ve brought up the fact that all monads are applicatives many times. Naperian applicative functor zips together data structure that are fixed in shape.

Appliactive functors were originally named idom by McBride and Paterson, so Gibbons uses the term idiomatic interchangably with applicative througout this paper, even though McBride and Paterson renamed it to applicative functors.

Monoidal applicative functors using Const datatype 

A second family of applicative functors, this time non-monadic, arises from constant functors with monoidal targets.

We can derive an applicative functor from any Monoid, by using empty for pure, and |+| for ap. The Const datatype is also called Const in Cats:

/**
 * [[Const]] is a phantom type, it does not contain a value of its second type parameter `B`
 * [[Const]] can be seen as a type level version of `Function.const[A, B]: A => B => A`
 */
final case class Const[A, B](getConst: A) {
  /**
   * changes the type of the second type parameter
   */
  def retag[C]: Const[A, C] =
    this.asInstanceOf[Const[A, C]]

  ....
}

In the above, the type parameter A represents the value, but B is a phantom type used to make Functor happy.

import cats._, cats.data._, cats.syntax.all._

Const(1) map { (_: String) + "!" }
// res0: Const[Int, String] = Const(getConst = 1)

When A forms a Semigroup, an Apply is derived, and when A form a Monoid, an Applicative is derived automatically.

Computations within this applicative functor accumulate some measure: for the monoid of integers with addition, they count or sum…

Const(2).retag[String => String] ap Const(1).retag[String]
// res1: Const[Int, String] = Const(getConst = 3)

Combining applicative functors 

EIP:

Like monads, applicative functors are closed under products; so two independent idiomatic effects can generally be fused into one, their product.

Cats seems to be missing the functor products altogether.

Product of functors 

(The impelementation I wrote here got merged into Cats in #388, and then it became Tuple2K)

/**
 * [[Tuple2K]] is a product to two independent functor values.
 *
 * See: [[https://www.cs.ox.ac.uk/jeremy.gibbons/publications/iterator.pdf The Essence of the Iterator Pattern]]
 */
final case class Tuple2K[F[_], G[_], A](first: F[A], second: G[A]) {

  /**
   * Modify the context `G` of `second` using transformation `f`.
   */
  def mapK[H[_]](f: G ~> H): Tuple2K[F, H, A] =
    Tuple2K(first, f(second))

}

First we start with the product of Functor:

private[data] sealed abstract class Tuple2KInstances8 {
  implicit def catsDataFunctorForTuple2K[F[_], G[_]](implicit FF: Functor[F], GG: Functor[G]): Functor[λ[α => Tuple2K[F, G, α]]] = new Tuple2KFunctor[F, G] {
    def F: Functor[F] = FF
    def G: Functor[G] = GG
  }
}

private[data] sealed trait Tuple2KFunctor[F[_], G[_]] extends Functor[λ[α => Tuple2K[F, G, α]]] {
  def F: Functor[F]
  def G: Functor[G]
  override def map[A, B](fa: Tuple2K[F, G, A])(f: A => B): Tuple2K[F, G, B] = Tuple2K(F.map(fa.first)(f), G.map(fa.second)(f))
}

Here’s how to use it:

import cats._, cats.data._, cats.syntax.all._

val x = Tuple2K(List(1), 1.some)
// x: Tuple2K[List, Option, Int] = Tuple2K(
//   first = List(1),
//   second = Some(value = 1)
// )

Functor[Lambda[X => Tuple2K[List, Option, X]]].map(x) { _ + 1 }
// res0: Tuple2K[List[A], Option, Int] = Tuple2K(
//   first = List(2),
//   second = Some(value = 2)
// )

First, we are defining a pair-like datatype called Tuple2K, which prepresents a product of typeclass instances. By simply passing the function f to both the sides, we can form Functor for Tuple2K[F, G] where F and G are Functor.

To see if it worked, we are mapping over x and adding 1. We could make the usage code a bit nicer if we wanted, but it’s ok for now.

Product of apply functors 

Next up is Apply:

private[data] sealed abstract class Tuple2KInstances6 extends Tuple2KInstances7 {
  implicit def catsDataApplyForTuple2K[F[_], G[_]](implicit FF: Apply[F], GG: Apply[G]): Apply[λ[α => Tuple2K[F, G, α]]] = new Tuple2KApply[F, G] {
    def F: Apply[F] = FF
    def G: Apply[G] = GG
  }
}

private[data] sealed trait Tuple2KApply[F[_], G[_]] extends Apply[λ[α => Tuple2K[F, G, α]]] with Tuple2KFunctor[F, G] {
  def F: Apply[F]
  def G: Apply[G]
  ....
}

Here’s the usage:

{
  val x = Tuple2K(List(1), (Some(1): Option[Int]))

  val f = Tuple2K(List((_: Int) + 1), (Some((_: Int) * 3): Option[Int => Int]))

  Apply[Lambda[X => Tuple2K[List, Option, X]]].ap(f)(x)
}
// res1: Tuple2K[List[A], Option, Int] = Tuple2K(
//   first = List(2),
//   second = Some(value = 3)
// )

The product of Apply passed in separate functions to each side.

Product of applicative functors 

Finally we can implement the product of Applicative:

private[data] sealed abstract class Tuple2KInstances5 extends Tuple2KInstances6 {
  implicit def catsDataApplicativeForTuple2K[F[_], G[_]](implicit FF: Applicative[F], GG: Applicative[G]): Applicative[λ[α => Tuple2K[F, G, α]]] = new Tuple2KApplicative[F, G] {
    def F: Applicative[F] = FF
    def G: Applicative[G] = GG
  }
}

private[data] sealed trait Tuple2KApplicative[F[_], G[_]] extends Applicative[λ[α => Tuple2K[F, G, α]]] with Tuple2KApply[F, G] {
  def F: Applicative[F]
  def G: Applicative[G]
  def pure[A](a: A): Tuple2K[F, G, A] = Tuple2K(F.pure(a), G.pure(a))
}

Here’s a simple usage:

Applicative[Lambda[X => Tuple2K[List, Option, X]]].pure(1)
// res2: Tuple2K[List[A], Option, Int] = Tuple2K(
//   first = List(1),
//   second = Some(value = 1)
// )

We were able to create Tuple2K(List(1), Some(1)) by calling pure(1).

Composition of Applicative 

Unlike monads in general, applicative functors are also closed under composition; so two sequentially-dependent idiomatic effects can generally be fused into one, their composition.

Thankfully Cats ships with the composition of Applicatives. There’s compose method in the typeclass instance:

@typeclass trait Applicative[F[_]] extends Apply[F] { self =>
  /**
   * `pure` lifts any value into the Applicative Functor
   *
   * Applicative[Option].pure(10) = Some(10)
   */
  def pure[A](x: A): F[A]

  /**
   * Two sequentially dependent Applicatives can be composed.
   *
   * The composition of Applicatives `F` and `G`, `F[G[x]]`, is also an Applicative
   *
   * Applicative[Option].compose[List].pure(10) = Some(List(10))
   */
  def compose[G[_]](implicit GG : Applicative[G]): Applicative[λ[α => F[G[α]]]] =
    new CompositeApplicative[F,G] {
      implicit def F: Applicative[F] = self
      implicit def G: Applicative[G] = GG
    }

  ....
}

Let’s try this out.

Applicative[List].compose[Option].pure(1)
// res3: List[Option[Int]] = List(Some(value = 1))

So much nicer.

Product of applicative functions 

For some reason, people seem to overlook that Gibbons also introduces applicative function composition operators in EIP. An applicative function is a function in the form of A => F[B] where F forms an Applicative. This is similar to Kleisli composition of monadic functions, but better.

Here’s why. Kliesli composition will let you compose A => F[B] and B => F[C] using andThen, but note that F stays the same. On the other hand, AppFunc composes A => F[B] and B => G[C].

/**
 * [[Func]] is a function `A => F[B]`.
 *
 * See: [[https://www.cs.ox.ac.uk/jeremy.gibbons/publications/iterator.pdf The Essence of the Iterator Pattern]]
 */
sealed abstract class Func[F[_], A, B] { self =>
  def run: A => F[B]
  def map[C](f: B => C)(implicit FF: Functor[F]): Func[F, A, C] =
    Func.func(a => FF.map(self.run(a))(f))
}

object Func extends FuncInstances {
  /** function `A => F[B]. */
  def func[F[_], A, B](run0: A => F[B]): Func[F, A, B] =
    new Func[F, A, B] {
      def run: A => F[B] = run0
    }

  /** applicative function. */
  def appFunc[F[_], A, B](run0: A => F[B])(implicit FF: Applicative[F]): AppFunc[F, A, B] =
    new AppFunc[F, A, B] {
      def F: Applicative[F] = FF
      def run: A => F[B] = run0
    }
}

....

/**
 * An implementation of [[Func]] that's specialized to [[Applicative]].
 */
sealed abstract class AppFunc[F[_], A, B] extends Func[F, A, B] { self =>
  def F: Applicative[F]

  def product[G[_]](g: AppFunc[G, A, B]): AppFunc[Lambda[X => Prod[F, G, X]], A, B] =
    {
      implicit val FF: Applicative[F] = self.F
      implicit val GG: Applicative[G] = g.F
      Func.appFunc[Lambda[X => Prod[F, G, X]], A, B]{
        a: A => Prod(self.run(a), g.run(a))
      }
    }

  ....
}

Here’s how we can use it:

{
  val f = Func.appFunc { x: Int => List(x.toString + "!") }

  val g = Func.appFunc { x: Int => (Some(x.toString + "?"): Option[String]) }

  val h = f product g

  h.run(1)
}
// res4: Tuple2K[List, Option[A], String] = Tuple2K(
//   first = List("1!"),
//   second = Some(value = "1?")
// )

As you can see two applicative functions are running side by side.

Composition of applicative functions 

Here’s andThen and compose:

  def compose[G[_], C](g: AppFunc[G, C, A]): AppFunc[Lambda[X => G[F[X]]], C, B] =
    {
      implicit val FF: Applicative[F] = self.F
      implicit val GG: Applicative[G] = g.F
      implicit val GGFF: Applicative[Lambda[X => G[F[X]]]] = GG.compose(FF)
      Func.appFunc[Lambda[X => G[F[X]]], C, B]({
        c: C => GG.map(g.run(c))(self.run)
      })
    }

  def andThen[G[_], C](g: AppFunc[G, B, C]): AppFunc[Lambda[X => F[G[X]]], A, C] =
    g.compose(self)

{
  val f = Func.appFunc { x: Int => List(x.toString + "!") }

  val g = Func.appFunc { x: String => (Some(x + "?"): Option[String]) }

  val h = f andThen g

  h.run(1)
}
// res5: Nested[List, Option[A], String] = Nested(
//   value = List(Some(value = "1!?"))
// )

EIP:

The two operators [snip] allow us to combine idiomatic computations in two different ways; we call them parallel and sequential composition, respectively.

The combining applicative computation is an abstract concept for all Applicative. We’ll continue from here.

day 12 

On day 11 we started reading Jeremy Gibbons’s Datatype-Generic Programming. We saw the creative use of Fix and Bifunctor,

When we moved on to The Essence of the Iterator Pattern, we found that Cats uses Const to represent monoidal applicatives like Int, but it’s currently missing a way to compose applicative functions.

We started with a datatype called Tuple2K that represents a pair of F[A] and G[A], then we also added AppFunc that represents applicative functions. #388

Traverse 

The Essence of the Iterator Pattern:

Two of the three motivating examples McBride and Paterson provide for idiomatic computations — sequencing a list of monadic effects and transposing a matrix — are instances of a general scheme they call traversal. This involves iterating over the elements of a data structure, in the style of a map, but interpreting certain function applications idiomatically. … We capture this via a type class of Traversable data structures.

In Cats, this typeclass is called Traverse:

@typeclass trait Traverse[F[_]] extends Functor[F] with Foldable[F] { self =>

  /**
   * given a function which returns a G effect, thread this effect
   * through the running of this function on all the values in F,
   * returning an F[A] in a G context
   */
  def traverse[G[_]: Applicative, A, B](fa: F[A])(f: A => G[B]): G[F[B]]

  /**
   * thread all the G effects through the F structure to invert the
   * structure from F[G[_]] to G[F[_]]
   */
  def sequence[G[_]: Applicative, A](fga: F[G[A]]): G[F[A]] =
    traverse(fga)(ga => ga)
  ....
}

Note that the f takes the shape of A => G[B].

When m is specialised to the identity applicative functor, traversal reduces precisely (modulo the wrapper) to the functorial map over lists.

Cats’ identity applicative functor is defined as follows:

  type Id[A] = A
  implicit val Id: Bimonad[Id] =
    new Bimonad[Id] {
      def pure[A](a: A): A = a
      def extract[A](a: A): A = a
      def flatMap[A, B](a: A)(f: A => B): B = f(a)
      def coflatMap[A, B](a: A)(f: A => B): B = f(a)
      override def map[A, B](fa: A)(f: A => B): B = f(fa)
      override def ap[A, B](fa: A)(ff: A => B): B = ff(fa)
      override def flatten[A](ffa: A): A = ffa
      override def map2[A, B, Z](fa: A, fb: B)(f: (A, B) => Z): Z = f(fa, fb)
      override def lift[A, B](f: A => B): A => B = f
      override def imap[A, B](fa: A)(f: A => B)(fi: B => A): B = f(fa)
  }

Here’s how we can traverse over List(1, 2, 3) using Id.

import cats._, cats.data._, cats.syntax.all._

List(1, 2, 3) traverse[Id, Int] { (x: Int) => x + 1 }
// res0: Id[List[Int]] = List(2, 3, 4)

In the case of a monadic applicative functor, traversal specialises to monadic map, and has the same uses. In fact, traversal is really just a slight generalisation of monadic map.

Let’s try using this for List:

List(1, 2, 3) traverse { (x: Int) => (Some(x + 1): Option[Int]) }
// res1: Option[List[Int]] = Some(value = List(2, 3, 4))

List(1, 2, 3) traverse { (x: Int) => None }
// res2: Option[List[Nothing]] = None

For a Naperian applicative functor, traversal transposes results.

We’re going to skip this one.

For a monoidal applicative functor, traversal accumulates values. The function reduce performs that accumulation, given an argument that assigns a value to each element

def reduce[A, B, F[_]](fa: F[A])(f: A => B)
  (implicit FF: Traverse[F], BB: Monoid[B]): B =
  {
    val g: A => Const[B, Unit] = { (a: A) => Const((f(a))) }
    val x = FF.traverse[Const[B, *], A, Unit](fa)(g)
    x.getConst
  }

Here’s how we can use this:

reduce(List('a', 'b', 'c')) { c: Char => c.toInt }
// res3: Int = 294

Thanks to partial unification (default in Scala 2.13, and -Ypartial-unification in 2.12), traverse is able to infer the types:

def reduce[A, B, F[_]](fa: F[A])(f: A => B)
  (implicit FF: Traverse[F], BB: Monoid[B]): B =
  {
    val x = fa traverse { (a: A) => Const[B, Unit]((f(a))) }
    x.getConst
  }

We’ll find out what this is about later.

sequence function 

Applicative and Traverse are mentioned together by McBride and Paterson in Applicative programming with effects.

As a background, until a few months ago (March 2015), the sequence function in Control.Monad package used to look like this:

-- | Evaluate each action in the sequence from left to right,
-- and collect the results.
sequence :: Monad m => [m a] -> m [a]

If I translate this into Scala, it would look like:

def sequence[G[_]: Monad, A](gas: List[G[A]]): G[List[A]]

It takes a list of monadic values, and returns a monadic value of a list. This already looks pretty useful on its own, but whenever you find a hardcoded List like this, we should suspect if it should be replaced with a better typeclass.

McBride and Paterson first generalized the sequence function to dist, by replacing Monad with Applicative:

def dist[G[_]: Applicative, A](gas: List[G[A]]): G[List[A]]

Next, they realized that dist is often called with map so they added another parameter for applicative function, and called it traverse:

def traverse[G[_]: Applicative, A, B](as: List[A])(f: A => G[B]): G[List[B]]

Finally they generalized the above signature into a typeclass named Traversible:

@typeclass trait Traverse[F[_]] extends Functor[F] with Foldable[F] { self =>

  /**
   * given a function which returns a G effect, thread this effect
   * through the running of this function on all the values in F,
   * returning an F[A] in a G context
   */
  def traverse[G[_]: Applicative, A, B](fa: F[A])(f: A => G[B]): G[F[B]]

  /**
   * thread all the G effects through the F structure to invert the
   * structure from F[G[_]] to G[F[_]]
   */
  def sequence[G[_]: Applicative, A](fga: F[G[A]]): G[F[A]] =
    traverse(fga)(ga => ga)
  ....
}

Thus as the matter of course, Traverse implements a datatype-generic, sequence function, which is just traverse with identity, conceptually easier to remember, because it simply flips F[G[A]] into G[F[A]]. You might have seen this function for Future in the standard library.

import scala.concurrent.{ Future, ExecutionContext, Await }
import scala.concurrent.duration._

val x = {
  implicit val ec = scala.concurrent.ExecutionContext.global
  List(Future { 1 }, Future { 2 }).sequence
}
// x: Future[List[Int]] = Future(Success(List(1, 2)))

Await.result(x, 1 second)
// res5: List[Int] = List(1, 2)

Another useseful thing might be to turn a List of Either into an Either.

List(Right(1): Either[String, Int]).sequence
// res6: Either[String, List[Int]] = Right(value = List(1))

List(Right(1): Either[String, Int], Left("boom"): Either[String, Int]).sequence
// res7: Either[String, List[Int]] = Left(value = "boom")

Note that we no longer need sequenceU.

TraverseFilter 

/**
 * `TraverseFilter`, also known as `Witherable`, represents list-like structures
 * that can essentially have a `traverse` and a `filter` applied as a single
 * combined operation (`traverseFilter`).
 *
 * Based on Haskell's [[https://hackage.haskell.org/package/witherable-0.1.3.3/docs/Data-Witherable.html Data.Witherable]]
 */
@typeclass
trait TraverseFilter[F[_]] extends FunctorFilter[F] {
  def traverse: Traverse[F]

  final override def functor: Functor[F] = traverse

  /**
   * A combined [[traverse]] and [[filter]]. Filtering is handled via `Option`
   * instead of `Boolean` such that the output type `B` can be different than
   * the input type `A`.
   *
   * Example:
   * {{{
   * scala> import cats.implicits._
   * scala> val m: Map[Int, String] = Map(1 -> "one", 3 -> "three")
   * scala> val l: List[Int] = List(1, 2, 3, 4)
   * scala> def asString(i: Int): Eval[Option[String]] = Now(m.get(i))
   * scala> val result: Eval[List[String]] = l.traverseFilter(asString)
   * scala> result.value
   * res0: List[String] = List(one, three)
   * }}}
   */
  def traverseFilter[G[_], A, B](fa: F[A])(f: A => G[Option[B]])(implicit G: Applicative[G]): G[F[B]]

  def sequenceFilter[G[_], A](fgoa: F[G[Option[A]]])(implicit G: Applicative[G]): G[F[A]] =
    traverseFilter(fgoa)(identity)

  def filterA[G[_], A](fa: F[A])(f: A => G[Boolean])(implicit G: Applicative[G]): G[F[A]] =
    traverseFilter(fa)(a => G.map(f(a))(if (_) Some(a) else None))

  def traverseEither[G[_], A, B, E](
    fa: F[A]
  )(f: A => G[Either[E, B]])(g: (A, E) => G[Unit])(implicit G: Monad[G]): G[F[B]] =
    traverseFilter(fa)(a =>
      G.flatMap(f(a)) {
        case Left(e)  => G.as(g(a, e), Option.empty[B])
        case Right(b) => G.pure(Some(b))
      }
    )

  override def mapFilter[A, B](fa: F[A])(f: A => Option[B]): F[B] =
    traverseFilter[Id, A, B](fa)(f)

  /**
   * Removes duplicate elements from a list, keeping only the first occurrence.
   */
  def ordDistinct[A](fa: F[A])(implicit O: Order[A]): F[A] = {
    implicit val ord: Ordering[A] = O.toOrdering

    traverseFilter[State[TreeSet[A], *], A, A](fa)(a =>
      State(alreadyIn => if (alreadyIn(a)) (alreadyIn, None) else (alreadyIn + a, Some(a)))
    )
      .run(TreeSet.empty)
      .value
      ._2
  }

  /**
   * Removes duplicate elements from a list, keeping only the first occurrence.
   * This is usually faster than ordDistinct, especially for things that have a slow comparion (like String).
   */
  def hashDistinct[A](fa: F[A])(implicit H: Hash[A]): F[A] =
    traverseFilter[State[HashSet[A], *], A, A](fa)(a =>
      State(alreadyIn => if (alreadyIn(a)) (alreadyIn, None) else (alreadyIn + a, Some(a)))
    )
      .run(HashSet.empty)
      .value
      ._2
}

filterA 

filterA is a more generalized (or weaker) version of filterM. Instead of requiring a Monad[G] it needs Applicative[G].

Here’s how we can use this:

import cats._, cats.syntax.all._

List(1, 2, 3) filterA { x => List(true, false) }
// res0: List[List[Int]] = List(
//   List(1, 2, 3),
//   List(1, 2),
//   List(1, 3),
//   List(1),
//   List(2, 3),
//   List(2),
//   List(3),
//   List()
// )

Vector(1, 2, 3) filterA { x => Vector(true, false) }
// res1: Vector[Vector[Int]] = Vector(
//   Vector(1, 2, 3),
//   Vector(1, 2),
//   Vector(1, 3),
//   Vector(1),
//   Vector(2, 3),
//   Vector(2),
//   Vector(3),
//   Vector()
// )

Coercing type inference using partial unification 

EIP:

We will have a number of new datatypes with coercion functions like Id, unId, Const and unConst. To reduce clutter, we introduce a common notation for such coercions.

In Scala, implicits and type inference take us pretty far. But by dealing with typeclass a lot, we also end up seeing some of the weaknesses of Scala’s type inference. One of the issues we come across frequently is its inability to infer partially applied parameterized type, also known as SI-2712.

This was fixed by Miles Sabin in scala#5102 as ”-Ypartial-unification” flag. See also Explaining Miles’s Magic.

Here’s an example that Daniel uses:

def foo[F[_], A](fa: F[A]): String = fa.toString

foo { x: Int => x * 2 }
// res0: String = "<function1>"

The above did not compile before.

The reason it does not compile is because Function1 takes two type parameters, whereas F[_] only takes one.

With -Ypartial-unification it will now compile, but it’s important to understand that the compiler will now assume that the type constructors can be partially applied from left to right. In short, this will reward right-biased datatypes like Either, but you could end up with wrong answer if the datatype is left-biased.

In 2019, Scala 2.13.0 was released with partial unification enabled by default.

Shape and contents 

EIP:

In addition to being parametrically polymorphic in the collection elements, the generic traverse operation is parametrised along two further dimensions: the datatype being traversed, and the applicative functor in which the traversal is interpreted. Specialising the latter to lists as a monoid yields a generic contents operation:

Here’s how we can implement this with Cats:

import cats._, cats.data._, cats.syntax.all._

def contents[F[_], A](fa: F[A])(implicit FF: Traverse[F]): Const[List[A], F[Unit]] =
  {
    val contentsBody: A => Const[List[A], Unit] = { (a: A) => Const(List(a)) }
    FF.traverse(fa)(contentsBody)
  }

Now we can take any datatype that supports Traverse and turn it into a List.

contents(Vector(1, 2, 3)).getConst
// res0: List[Int] = List(1, 2, 3)

I am actually not sure if the result suppose to come out in the reverse order here.

The other half of the decomposition is obtained simply by a map, which is to say, a traversal interpreted in the identity idiom.

When Gibbons say identity idiom, he means the identity applicative functor, Id[_].

def shape[F[_], A](fa: F[A])(implicit FF: Traverse[F]): Id[F[Unit]] =
  {
    val shapeBody: A => Id[Unit] = { (a: A) => () }
    FF.traverse(fa)(shapeBody)
  }

Here’s the shape for Vector(1, 2, 3):

shape(Vector(1, 2, 3))
// res1: Id[Vector[Unit]] = Vector((), (), ())

EIP:

This pair of traversals nicely illustrates the two aspects of iterations that we are focussing on, namely mapping and accumulation.

Next EIP demonstrates applicative composition by first combining shape and contents together like this:

def decompose[F[_], A](fa: F[A])(implicit FF: Traverse[F]) =
  Tuple2K[Const[List[A], *], Id, F[Unit]](contents(fa), shape(fa))

val d = decompose(Vector(1, 2, 3))
// d: Tuple2K[Const[List[Int], β0], Id, Vector[Unit]] = Tuple2K(
//   first = Const(getConst = List(1, 2, 3)),
//   second = Vector((), (), ())
// )

d.first
// res2: Const[List[Int], Vector[Unit]] = Const(getConst = List(1, 2, 3))

d.second
// res3: Id[Vector[Unit]] = Vector((), (), ())

The problem here is that we are running traverse twice.

Is it possible to fuse the two traversals into one? The product of applicative functors allows exactly this.

Let’s try rewriting this using AppFunc.

import cats.data.Func.appFunc

def contentsBody[A]: AppFunc[Const[List[A], *], A, Unit] =
  appFunc[Const[List[A], *], A, Unit] { (a: A) => Const(List(a)) }

def shapeBody[A]: AppFunc[Id, A, Unit] =
  appFunc { (a: A) => ((): Id[Unit]) }

def decompose[F[_], A](fa: F[A])(implicit FF: Traverse[F]) =
  (contentsBody[A] product shapeBody[A]).traverse(fa)

val d = decompose(Vector(1, 2, 3))
// d: Tuple2K[Const[List[Int], β1], Id[A], Vector[Unit]] = Tuple2K(
//   first = Const(getConst = List(1, 2, 3)),
//   second = Vector((), (), ())
// )

d.first
// res5: Const[List[Int], Vector[Unit]] = Const(getConst = List(1, 2, 3))

d.second
// res6: Id[Vector[Unit]] = Vector((), (), ())

The return type of the decompose is a bit messy, but it’s infered by AppFunc: Tuple2K[Const[List[Int], β1], Id[A], Vector[Unit]].

Applicative wordcount 

Skipping over to section 6 of EIP “Modular programming with applicative functors.”

EIP:

There is an additional benefit of applicative functors over monads, which concerns the modular development of complex iterations from simpler aspects. ….

As an illustration, we consider the Unix word-counting utility wc, which computes the numbers of characters, words and lines in a text file.

We can translate the full example using applicative function composition, which is only available on my personal branch. (PR #388 is pending)

Modular iterations, applicatively 

import cats._, cats.data._, cats.syntax.all._
import Func.appFunc

The character-counting slice of the wc program accumulates a result in the integers-as-monoid applicative functor:

Here’s a type alias to treat Int as a monoidal applicative:

type Count[A] = Const[Int, A]

In the above, A is a phantom type we don’t need, so let’s just hardcode it to Unit:

def liftInt(i: Int): Count[Unit] = Const(i)
def count[A](a: A): Count[Unit] = liftInt(1)

The body of the iteration simply yields 1 for every element:

lazy val countChar: AppFunc[Count, Char, Unit] = appFunc(count)

To use this AppFunc, we would call traverse with List[Char]. Here’s a quote I found from Hamlet.

lazy val text = ("Faith, I must leave thee, love, and shortly too.\n" +
           "My operant powers their functions leave to do.\n").toList

countChar traverse text
// res0: Count[List[Unit]] = Const(getConst = 96)

This looks ok.

Counting the lines (in fact, the newline characters, thereby ignoring a final ‘line’ that is not terminated with a newline character) is similar: the difference is simply what number to use for each element, namely 1 for a newline and 0 for anything else.

def testIf(b: Boolean): Int = if (b) 1 else 0

lazy val countLine: AppFunc[Count, Char, Unit] =
  appFunc { (c: Char) => liftInt(testIf(c === '\n')) }

Again, to use this we’ll just call traverse:

countLine traverse text
// res1: Count[List[Unit]] = Const(getConst = 2)

Counting the words is trickier, because it necessarily involves state. Here, we use the State monad with a boolean state, indicating whether we are currently within a word, and compose this with the applicative functor for counting.

def isSpace(c: Char): Boolean = (c === ' ' || c === '\n' || c === '\t')

lazy val countWord =
  appFunc { (c: Char) =>
    import cats.data.State.{ get, set }
    for {
      x <- get[Boolean]
      y = !isSpace(c)
      _ <- set(y)
    } yield testIf(y && !x)
  } andThen appFunc(liftInt)

Traversing this AppFunc returns a State datatype:

val x = countWord traverse text
// x: Nested[IndexedStateT[Eval, Boolean, Boolean, A], Count[A], List[Unit]] = Nested(
//   value = cats.data.IndexedStateT@dc69548
// )

We then need to run this state machine with an initial value false to get the result:

x.value.runA(false).value
// res2: Count[List[Unit]] = Const(getConst = 17)

17 words.

Like we did with shape and content, we can fuse the traversal into one shot by combining the applicative functions.

lazy val countAll = countWord
  .product(countLine)
  .product(countChar)

val allResults = countAll traverse text
// allResults: Tuple2K[Tuple2K[Nested[IndexedStateT[Eval, Boolean, Boolean, A], Count[A], γ3], Count[A], α], Count[A], List[Unit]] = Tuple2K(
//   first = Tuple2K(
//     first = Nested(value = cats.data.IndexedStateT@4558bc76),
//     second = Const(getConst = 2)
//   ),
//   second = Const(getConst = 96)
// )

val charCount = allResults.second
// charCount: Count[List[Unit]] = Const(getConst = 96)

val lineCount = allResults.first.second
// lineCount: Count[List[Unit]] = Const(getConst = 2)

val wordCountState = allResults.first.first
// wordCountState: Nested[IndexedStateT[Eval, Boolean, Boolean, A], Count[A], List[Unit]] = Nested(
//   value = cats.data.IndexedStateT@4558bc76
// )

val wordCount = wordCountState.value.runA(false).value
// wordCount: Count[List[Unit]] = Const(getConst = 17)

EIP:

Applicative functors have a richer algebra of composition operators, which can often replace the use of monad transformers; there is the added advantage of being able to compose applicative but non-monadic computations.

That’s it for today.

day 13 

On day 12 we continued exploring The Essence of the Iterator Pattern, and looked at Traverse, shape and contents, and the applicative wordcount.

Id datatype 

We saw Id in passing while reading EIP, but it’s an interesting tool, so we should revisit it. This is also called Identity, Identity functor, or Identity monad, depending on the context. The definition of the datatype is quite simple:

  type Id[A] = A

Here’s with the documentation and the typeclass instances:

  /**
   * Identity, encoded as `type Id[A] = A`, a convenient alias to make
   * identity instances well-kinded.
   *
   * The identity monad can be seen as the ambient monad that encodes
   * the effect of having no effect. It is ambient in the sense that
   * plain pure values are values of `Id`.
   *
   * For instance, the [[cats.Functor]] instance for `[[cats.Id]]`
   * allows us to apply a function `A => B` to an `Id[A]` and get an
   * `Id[B]`. However, an `Id[A]` is the same as `A`, so all we're doing
   * is applying a pure function of type `A => B` to a pure value  of
   * type `A` to get a pure value of type `B`. That is, the instance
   * encodes pure unary function application.
   */
  type Id[A] = A

  implicit val catsInstancesForId
    : Bimonad[Id] with CommutativeMonad[Id] with Comonad[Id] with NonEmptyTraverse[Id] with Distributive[Id] =
    new Bimonad[Id] with CommutativeMonad[Id] with Comonad[Id] with NonEmptyTraverse[Id] with Distributive[Id] {
      def pure[A](a: A): A = a
      def extract[A](a: A): A = a
      def flatMap[A, B](a: A)(f: A => B): B = f(a)
      def coflatMap[A, B](a: A)(f: A => B): B = f(a)
      @tailrec def tailRecM[A, B](a: A)(f: A => Either[A, B]): B =
        f(a) match {
          case Left(a1) => tailRecM(a1)(f)
          case Right(b) => b
        }
      override def distribute[F[_], A, B](fa: F[A])(f: A => B)(implicit F: Functor[F]): Id[F[B]] = F.map(fa)(f)
      override def map[A, B](fa: A)(f: A => B): B = f(fa)
      override def ap[A, B](ff: A => B)(fa: A): B = ff(fa)
      override def flatten[A](ffa: A): A = ffa
      override def map2[A, B, Z](fa: A, fb: B)(f: (A, B) => Z): Z = f(fa, fb)
      override def lift[A, B](f: A => B): A => B = f
      override def imap[A, B](fa: A)(f: A => B)(fi: B => A): B = f(fa)
      def foldLeft[A, B](a: A, b: B)(f: (B, A) => B) = f(b, a)
      def foldRight[A, B](a: A, lb: Eval[B])(f: (A, Eval[B]) => Eval[B]): Eval[B] =
        f(a, lb)
      def nonEmptyTraverse[G[_], A, B](a: A)(f: A => G[B])(implicit G: Apply[G]): G[B] =
        f(a)
      override def foldMap[A, B](fa: Id[A])(f: A => B)(implicit B: Monoid[B]): B = f(fa)
      override def reduce[A](fa: Id[A])(implicit A: Semigroup[A]): A =
        fa
      def reduceLeftTo[A, B](fa: Id[A])(f: A => B)(g: (B, A) => B): B =
        f(fa)
      override def reduceLeft[A](fa: Id[A])(f: (A, A) => A): A =
        fa
      override def reduceLeftToOption[A, B](fa: Id[A])(f: A => B)(g: (B, A) => B): Option[B] =
        Some(f(fa))
      override def reduceRight[A](fa: Id[A])(f: (A, Eval[A]) => Eval[A]): Eval[A] =
        Now(fa)
      def reduceRightTo[A, B](fa: Id[A])(f: A => B)(g: (A, Eval[B]) => Eval[B]): Eval[B] =
        Now(f(fa))
      override def reduceRightToOption[A, B](fa: Id[A])(f: A => B)(g: (A, Eval[B]) => Eval[B]): Eval[Option[B]] =
        Now(Some(f(fa)))
      override def reduceMap[A, B](fa: Id[A])(f: A => B)(implicit B: Semigroup[B]): B = f(fa)
      override def size[A](fa: Id[A]): Long = 1L
      override def get[A](fa: Id[A])(idx: Long): Option[A] =
        if (idx == 0L) Some(fa) else None
      override def isEmpty[A](fa: Id[A]): Boolean = false
    }

Here’s how to create a value of Id:

import cats._, cats.syntax.all._

val one: Id[Int] = 1
// one: Id[Int] = 1

Id as Functor 

The functor instance for Id is same as function application:

Functor[Id].map(one) { _ + 1 }
// res0: Id[Int] = 2

Id as Apply 

The apply’s ap method, which takes Id[A => B], but in reality just A => B is also implemented as function application:

Apply[Id].ap({ _ + 1 }: Id[Int => Int])(one)
// res1: Id[Int] = 2

Id as FlatMap 

The FlatMap’s flatMap method, which takes A => Id[B] is the same story. It’s implemented function application:

FlatMap[Id].flatMap(one) { _ + 1 }
// res2: Id[Int] = 2

What’s the point of Id? 

At a glance, Id datatype is not very useful. The hint is in the Scaladoc of the definition: a convenient alias to make identity instances well-kinded. In other words, there are situations where we need to lift some type A into F[A], and Id can be used to just do that without introducing any effects. We’ll see an example of that later.

Eval datatype 

Cats also comes with Eval datatype that controls evaluation.

sealed abstract class Eval[+A] extends Serializable { self =>

  /**
   * Evaluate the computation and return an A value.
   *
   * For lazy instances (Later, Always), any necessary computation
   * will be performed at this point. For eager instances (Now), a
   * value will be immediately returned.
   */
  def value: A

  /**
   * Ensure that the result of the computation (if any) will be
   * memoized.
   *
   * Practically, this means that when called on an Always[A] a
   * Later[A] with an equivalent computation will be returned.
   */
  def memoize: Eval[A]
}

There are several ways to create an Eval value:

object Eval extends EvalInstances {

  /**
   * Construct an eager Eval[A] value (i.e. Now[A]).
   */
  def now[A](a: A): Eval[A] = Now(a)

  /**
   * Construct a lazy Eval[A] value with caching (i.e. Later[A]).
   */
  def later[A](a: => A): Eval[A] = new Later(a _)

  /**
   * Construct a lazy Eval[A] value without caching (i.e. Always[A]).
   */
  def always[A](a: => A): Eval[A] = new Always(a _)

  /**
   * Defer a computation which produces an Eval[A] value.
   *
   * This is useful when you want to delay execution of an expression
   * which produces an Eval[A] value. Like .flatMap, it is stack-safe.
   */
  def defer[A](a: => Eval[A]): Eval[A] =
    new Eval.Call[A](a _) {}

  /**
   * Static Eval instances for some common values.
   *
   * These can be useful in cases where the same values may be needed
   * many times.
   */
  val Unit: Eval[Unit] = Now(())
  val True: Eval[Boolean] = Now(true)
  val False: Eval[Boolean] = Now(false)
  val Zero: Eval[Int] = Now(0)
  val One: Eval[Int] = Now(1)

  ....
}

Eval.later 

The most useful one is Eval.later, which captures a by-name parameter in a lazy val.

import cats._, cats.data._, cats.syntax.all._

var g: Int = 0
// g: Int = 0

val x = Eval.later {
  g = g + 1
  g
}
// x: Eval[Int] = cats.Later@3de72742

g = 2

x.value
// res1: Int = 3

x.value
// res2: Int = 3

The value is cached, so the second evaluation doesn’t happen.

Eval.now 

Eval.now evaluates eagerly, and then captures the result in a field, so the second evaluation doesn’t happen.

val y = Eval.now {
  g = g + 1
  g
}
// y: Eval[Int] = Now(value = 4)

y.value
// res3: Int = 4

y.value
// res4: Int = 4

Eval.always 

Eval.always doesn’t cache.

val z = Eval.always {
  g = g + 1
  g
}
// z: Eval[Int] = cats.Always@56362dbb

z.value
// res5: Int = 5

z.value
// res6: Int = 6

stack-safe lazy computation 

One useful feature of Eval is that it supports stack-safe lazy computation via map and flatMap methods, which use an internal trampoline to avoid stack overflow.

You can also defer a computation which produces Eval[A] value using Eval.defer. Here’s how foldRight is implemented for List for example:

def foldRight[A, B](fa: List[A], lb: Eval[B])(f: (A, Eval[B]) => Eval[B]): Eval[B] = {
  def loop(as: List[A]): Eval[B] =
    as match {
      case Nil => lb
      case h :: t => f(h, Eval.defer(loop(t)))
    }
  Eval.defer(loop(fa))
}

Let’s try blowing up the stack on purpose:

scala> :paste
object OddEven0 {
  def odd(n: Int): String = even(n - 1)
  def even(n: Int): String = if (n <= 0) "done" else odd(n - 1)
}

// Exiting paste mode, now interpreting.

defined object OddEven0

scala> OddEven0.even(200000)
java.lang.StackOverflowError
  at OddEven0$.even(<console>:15)
  at OddEven0$.odd(<console>:14)
  at OddEven0$.even(<console>:15)
  at OddEven0$.odd(<console>:14)
  at OddEven0$.even(<console>:15)
  ....

Here’s my attempt at making a safer version:

object OddEven1 {
  def odd(n: Int): Eval[String] = Eval.defer {even(n - 1)}
  def even(n: Int): Eval[String] =
    Eval.now { n <= 0 } flatMap {
      case true => Eval.now {"done"}
      case _    => Eval.defer { odd(n - 1) }
    }
}

OddEven1.even(200000).value
// res7: String = "done"

In the earlier versions of Cats the above caused stack overflow, but as BryanM let me know in the comment, David Gregory fixed it in #769, so it works now.

The Abstract Future 

One blog post that I occasionally see being mentioned as a poweful application of monad, especially in the context of building large application is The Abstract Future. It was originally posted to the precog.com engineering blog on November 27, 2012 by Kris Nuttycombe (@nuttycom).

At Precog, we use Futures extensively, both in a direct fashion and to allow us a composable way to interact with subsystems that are implemented atop Akka’s actor framework. Futures are arguably one of the best tools we have for reining in the complexity of asynchronous programming, and so our many of our early versions of APIs in our codebase exposed Futures directly. ….

What this means is that from the perspective of the consumer of the DatasetModule interface, the only aspect of Future that we’re relying upon is the ability to order operations in a statically checked fashion; the sequencing, rather than any particular semantics related to Future’s asynchrony, is the relevant piece of information provided by the type. So, the following generalization becomes natural.

Here I’ll use similar example as the Yoshida-san’s.

import cats._, cats.data._, cats.syntax.all._

case class User(id: Long, name: String)

// In actual code, probably more than 2 errors
sealed trait Error
object Error {
  final case class UserNotFound(userId: Long) extends Error
  final case class ConnectionError(message: String) extends Error
}

trait UserRepos[F[_]] {
  implicit def F: Monad[F]
  def userRepo: UserRepo
  trait UserRepo {
    def followers(userId: Long): F[List[User]]
  }
}

UserRepos with Future 

Let’s start implementing the UserRepos module using Future.

import scala.concurrent.{ Future, ExecutionContext, Await }
import scala.concurrent.duration.Duration

class UserRepos0(implicit ec: ExecutionContext) extends UserRepos[Future] {
  override val F = implicitly[Monad[Future]]
  override val userRepo: UserRepo = new UserRepo0 {}
  trait UserRepo0 extends UserRepo {
    def followers(userId: Long): Future[List[User]] = Future.successful { Nil }
  }
}

Here’s how to use it:

{
  val service = new UserRepos0()(ExecutionContext.global)
  service.userRepo.followers(1L)
}
// res0: Future[List[User]] = Future(Success(List()))

Now we have an asynchronous result. Let’s say during testing we would like it to be synchronous.

UserRepos with Id 

In a test, we probably don’t want to worry about the fact that the computation is being performed asynchronously; all that we care about is that we obtain a correct result. ….

For most cases, we’ll use the identity monad for testing. Suppose that we’re testing the piece of functionality described earlier, which has computed a result from the combination of a load, a sort, take and reduce. The test framework need never consider the monad that it’s operating in.

This is where Id datatype can be used.

class TestUserRepos extends UserRepos[Id] {
  override val F = implicitly[Monad[Id]]
  override val userRepo: UserRepo = new UserRepo0 {}
  trait UserRepo0 extends UserRepo {
    def followers(userId: Long): List[User] =
      userId match {
        case 0L => List(User(1, "Michael"))
        case 1L => List(User(0, "Vito"))
        case x =>  sys.error("not found")
      }
  }
}

Here’s how to use it:

val testRepo = new TestUserRepos {}
// testRepo: TestUserRepos = repl.MdocSession3@7d27c0e1

val ys = testRepo.userRepo.followers(1L)
// ys: Id[List[User]] = List(User(id = 0L, name = "Vito"))

Coding in abstract 

Now that we were able to abtract the type constructor of the followers, let’s try implementing isFriends from day 10 that checks if two users follow each other.

trait UserServices0[F[_]] { this: UserRepos[F] =>
  def userService: UserService = new UserService
  class UserService {
    def isFriends(user1: Long, user2: Long): F[Boolean] =
      F.flatMap(userRepo.followers(user1)) { a =>
        F.map(userRepo.followers(user2)) { b =>
          a.exists(_.id == user2) && b.exists(_.id == user1)
        }
      }
  }
}

Here’s how to use it:

{
  val testService = new TestUserRepos with UserServices0[Id] {}
  testService.userService.isFriends(0L, 1L)
}
// res1: Id[Boolean] = true

The above demonstrates that isFriends can be written without knowing anything about F[] apart from the fact that it forms a Monad. It would be nice if I could use infix flatMap and map method while keeping F abstract. I tried creating FlatMapOps(fa) manually, but that resulted in abstract method error during runtime. The actM macro that we implemented on day 6 seems to work ok:

trait UserServices[F[_]] { this: UserRepos[F] =>
  def userService: UserService = new UserService
  class UserService {
    import example.MonadSyntax._
    def isFriends(user1: Long, user2: Long): F[Boolean] =
      actM[F, Boolean] {
        val a = userRepo.followers(user1).next
        val b = userRepo.followers(user2).next
        a.exists(_.id == user2) && b.exists(_.id == user1)
      }
  }
}

{
  val testService = new TestUserRepos with UserServices[Id] {}
  testService.userService.isFriends(0L, 1L)
}
// res2: Id[Boolean] = true

UserRepos with EitherT 

We can also use this with the EitherT with Future to carry a custom error type.

class UserRepos1(implicit ec: ExecutionContext) extends UserRepos[EitherT[Future, Error, *]] {
  override val F = implicitly[Monad[EitherT[Future, Error, *]]]
  override val userRepo: UserRepo = new UserRepo1 {}
  trait UserRepo1 extends UserRepo {
    def followers(userId: Long): EitherT[Future, Error, List[User]] =
      userId match {
        case 0L => EitherT.right(Future { List(User(1, "Michael")) })
        case 1L => EitherT.right(Future { List(User(0, "Vito")) })
        case x =>
          EitherT.left(Future.successful { Error.UserNotFound(x) })
      }
  }
}

Here’s how to use it:

{
  import scala.concurrent.duration._
  val service = {
    import ExecutionContext.Implicits._
    new UserRepos1 with UserServices[EitherT[Future, Error, *]] {}
  }

  Await.result(service.userService.isFriends(0L, 1L).value, 1 second)
}
// res3: Either[Error, Boolean] = Right(value = true)

Note that for all three versions of services, I was able to reuse the UserServices trait without any changes.

That’s it for today.

day 14 

On day 13 we looked at Id datatype, Eval datatype, and The Abstract Future.

SemigroupK 

Semigroup we saw on day 4 is a bread and butter of functional programming that shows up in many places.

import cats._, cats.syntax.all._

List(1, 2, 3) |+| List(4, 5, 6)
// res0: List[Int] = List(1, 2, 3, 4, 5, 6)

"one" |+| "two"
// res1: String = "onetwo"

There’s a similar typeclass called SemigroupK for type constructors F[_].

@typeclass trait SemigroupK[F[_]] { self =>

  /**
   * Combine two F[A] values.
   */
  @simulacrum.op("<+>", alias = true)
  def combineK[A](x: F[A], y: F[A]): F[A]

  /**
   * Given a type A, create a concrete Semigroup[F[A]].
   */
  def algebra[A]: Semigroup[F[A]] =
    new Semigroup[F[A]] {
      def combine(x: F[A], y: F[A]): F[A] = self.combineK(x, y)
    }
}

This enables combineK operator and its symbolic alias <+>. Let’s try using this.

List(1, 2, 3) <+> List(4, 5, 6)
// res2: List[Int] = List(1, 2, 3, 4, 5, 6)

Unlike Semigroup, SemigroupK works regardless of the type parameter of F[_].

Option as SemigroupK 

Option[A] forms a Semigroup only when the type parameter A forms a Semigroup. Let’s disrupt that by creating a datatype does not form a Semigroup:

case class Foo(x: String)

So this won’t work:

Foo("x").some |+| Foo("y").some
// error: value |+| is not a member of Option[repl.MdocSession.App.Foo]
// Foo("x").some |+| Foo("y").some
// ^^^^^^^^^^^^^^^^^

But this works fine:

Foo("x").some <+> Foo("y").some
// res4: Option[Foo] = Some(value = Foo(x = "x"))

There’s also a subtle difference in the behaviors of two typeclasses.

1.some |+| 2.some
// res5: Option[Int] = Some(value = 3)

1.some <+> 2.some
// res6: Option[Int] = Some(value = 1)

The Semigroup will combine the inner value of the Option whereas SemigroupK will just pick the first one.

SemigroupK laws 

trait SemigroupKLaws[F[_]] {
  implicit def F: SemigroupK[F]

  def semigroupKAssociative[A](a: F[A], b: F[A], c: F[A]): IsEq[F[A]] =
    F.combineK(F.combineK(a, b), c) <-> F.combineK(a, F.combineK(b, c))
}

MonoidK 

There’s also MonoidK.

@typeclass trait MonoidK[F[_]] extends SemigroupK[F] { self =>

  /**
   * Given a type A, create an "empty" F[A] value.
   */
  def empty[A]: F[A]

  /**
   * Given a type A, create a concrete Monoid[F[A]].
   */
  override def algebra[A]: Monoid[F[A]] =
    new Monoid[F[A]] {
      def empty: F[A] = self.empty
      def combine(x: F[A], y: F[A]): F[A] = self.combineK(x, y)
    }

  ....
}

This adds empty[A] function to the contract. The notion of emptiness here is defined in terms of the left and right identity laws with regards to combineK. Given that combine and combineK behave differently, Monoid[F[A]].empty and MonoidK[F].empty[A] could also be different.

import cats._, cats.syntax.all._

Monoid[Option[Int]].empty
// res0: Option[Int] = None

MonoidK[Option].empty[Int]
// res1: Option[Int] = None

In case of Option[Int] they happened to be both None.

MonoidK laws 

trait MonoidKLaws[F[_]] extends SemigroupKLaws[F] {
  override implicit def F: MonoidK[F]

  def monoidKLeftIdentity[A](a: F[A]): IsEq[F[A]] =
    F.combineK(F.empty, a) <-> a

  def monoidKRightIdentity[A](a: F[A]): IsEq[F[A]] =
    F.combineK(a, F.empty) <-> a
}

Alternative 

There’s a typeclass that combines Applicative and MonoidK called Alternative:

@typeclass trait Alternative[F[_]] extends Applicative[F] with MonoidK[F] { self =>
   ....
}

Alternative on its own does not introduce any new methods or operators.

It’s more of a weaker (thus better) Applicative version of MonadPlus that adds filter on top of Monad. See day 3 to review the applicative style of coding.

Alternative laws 

trait AlternativeLaws[F[_]] extends ApplicativeLaws[F] with MonoidKLaws[F] {
  implicit override def F: Alternative[F]
  implicit def algebra[A]: Monoid[F[A]] = F.algebra[A]

  def alternativeRightAbsorption[A, B](ff: F[A => B]): IsEq[F[B]] =
    (ff ap F.empty[A]) <-> F.empty[B]

  def alternativeLeftDistributivity[A, B](fa: F[A], fa2: F[A], f: A => B): IsEq[F[B]] =
    ((fa |+| fa2) map f) <-> ((fa map f) |+| (fa2 map f))

  def alternativeRightDistributivity[A, B](fa: F[A], ff: F[A => B], fg: F[A => B]): IsEq[F[B]] =
    ((ff |+| fg) ap fa) <-> ((ff ap fa) |+| (fg ap fa))
}

There’s an open question by Yoshida-san on whether the last law is necessary or not.

Wolf, Goat, Cabbage 

Here’s Justin Le (@mstk)’s 2013 'Wolf, Goat, Cabbage: The List MonadPlus & Logic Problems.'.

Wolf, Goat, Cabbage: Solving simple logic problems in #haskell using the List MonadPlus :) http://t.co/YkKi6EQdDy

— Justin Le (@mstk) December 26, 2013

We can try implementing this using Alternative.

A farmer has a wolf, a goat, and a cabbage that he wishes to transport across a river. Unfortunately, his boat can carry only one thing at a time with him. He can’t leave the wolf alone with the goat, or the wolf will eat the goat. He can’t leave the goat alone with the cabbage, or the goat will eat the cabbage. How can he properly transport his belongings to the other side one at a time, without any disasters?

import cats._, cats.syntax.all._

sealed trait Character
case object Farmer extends Character
case object Wolf extends Character
case object Goat extends Character
case object Cabbage extends Character

case class Move(x: Character)

case class Plan(moves: List[Move])

sealed trait Position
case object West extends Position
case object East extends Position

implicit lazy val moveShow = Show.show[Move](_ match {
  case Move(Farmer)  => "F"
  case Move(Wolf)    => "W"
  case Move(Goat)    => "G"
  case Move(Cabbage) => "C"
})

makeNMoves0 

Here’s making n moves

val possibleMoves = List(Farmer, Wolf, Goat, Cabbage) map {Move(_)}
// possibleMoves: List[Move] = List(
//   Move(x = Farmer),
//   Move(x = Wolf),
//   Move(x = Goat),
//   Move(x = Cabbage)
// )

def makeMove0(ps: List[List[Move]]): List[List[Move]] =
  (ps , possibleMoves) mapN { (p, m) =>  List(m) <+> p }

def makeNMoves0(n: Int): List[List[Move]] =
  n match {
    case 0 => Nil
    case 1 => makeMove0(List(Nil))
    case n => makeMove0(makeNMoves0(n - 1))
  }

We can test this as follows:

makeNMoves0(1)
// res0: List[List[Move]] = List(
//   List(Move(x = Farmer)),
//   List(Move(x = Wolf)),
//   List(Move(x = Goat)),
//   List(Move(x = Cabbage))
// )

makeNMoves0(2)
// res1: List[List[Move]] = List(
//   List(Move(x = Farmer), Move(x = Farmer)),
//   List(Move(x = Wolf), Move(x = Farmer)),
//   List(Move(x = Goat), Move(x = Farmer)),
//   List(Move(x = Cabbage), Move(x = Farmer)),
//   List(Move(x = Farmer), Move(x = Wolf)),
//   List(Move(x = Wolf), Move(x = Wolf)),
//   List(Move(x = Goat), Move(x = Wolf)),
//   List(Move(x = Cabbage), Move(x = Wolf)),
//   List(Move(x = Farmer), Move(x = Goat)),
//   List(Move(x = Wolf), Move(x = Goat)),
//   List(Move(x = Goat), Move(x = Goat)),
//   List(Move(x = Cabbage), Move(x = Goat)),
//   List(Move(x = Farmer), Move(x = Cabbage)),
//   List(Move(x = Wolf), Move(x = Cabbage)),
//   List(Move(x = Goat), Move(x = Cabbage)),
//   List(Move(x = Cabbage), Move(x = Cabbage))
// )

isSolution 

Let’s define our helper function isSolution :: Plan -> Bool. Basically, we want to check if the positions of all of the characters are East.

We can define filter using just what’s available in Alternative:

def filterA[F[_]: Alternative, A](fa: F[A])(cond: A => Boolean): F[A] =
  {
    var acc = Alternative[F].empty[A]
    Alternative[F].map(fa) { x =>
      if (cond(x)) acc = Alternative[F].combineK(acc, Alternative[F].pure(x))
      else ()
    }
    acc
  }

def positionOf(p: List[Move], c: Character): Position =
  {
    def positionFromCount(n: Int): Position = {
      if (n % 2 == 0) West
      else East
    }
    c match {
      case Farmer => positionFromCount(p.size)
      case x      => positionFromCount(filterA(p)(_ == Move(c)).size)
    }
  }

val p = List(Move(Goat), Move(Farmer), Move(Wolf), Move(Goat))
// p: List[Move] = List(
//   Move(x = Goat),
//   Move(x = Farmer),
//   Move(x = Wolf),
//   Move(x = Goat)
// )

positionOf(p, Farmer)
// res2: Position = West

positionOf(p, Wolf)
// res3: Position = East

Here’s how we can check all positions are East:

def isSolution(p: List[Move]) =
  {
    val pos = (List(p), possibleMoves) mapN { (p, m) => positionOf(p, m.x) }
    (filterA(pos)(_ == West)).isEmpty
  }

makeMove 

What makes a move legal? Well, the farmer has to be on the same side as whatever is being moved.

def moveLegal(p: List[Move], m: Move): Boolean =
  positionOf(p, Farmer) == positionOf(p, m.x)

moveLegal(p, Move(Wolf))
// res4: Boolean = false

The plan is safe if nothing can eat anything else. That means if the wolf and goat or goat and cabbage sit on the same bank, so too must the farmer.

def safePlan(p: List[Move]): Boolean =
  {
    val posGoat = positionOf(p, Goat)
    val posFarmer = positionOf(p, Farmer)
    val safeGoat = posGoat != positionOf(p, Wolf)
    val safeCabbage = positionOf(p, Cabbage) != posGoat
    (posFarmer == posGoat) || (safeGoat && safeCabbage)
  }

Using these functions we can now re-implement makeMove:

def makeMove(ps: List[List[Move]]): List[List[Move]] =
  (ps, possibleMoves) mapN { (p, m) =>
    if (!moveLegal(p, m)) Nil
    else if (!safePlan(List(m) <+> p)) Nil
    else List(m) <+> p
  }

def makeNMoves(n: Int): List[List[Move]] =
  n match {
    case 0 => Nil
    case 1 => makeMove(List(Nil))
    case n => makeMove(makeNMoves(n - 1))
  }

def findSolution(n: Int): Unit =
  filterA(makeNMoves(n))(isSolution) map { p =>
    println(p map {_.show})
  }

Let’s try solving the puzzle:

findSolution(6)

findSolution(7)
// List(G, F, C, G, W, F, G)
// List(G, F, W, G, C, F, G)

findSolution(8)
// List(G, F, C, G, W, F, G)
// List(G, F, W, G, C, F, G)
// List(G, F, C, G, W, F, G)
// List(G, F, W, G, C, F, G)
// List(G, F, C, G, W, F, G)
// List(G, F, W, G, C, F, G)

It worked. That’s all for today.

day 15 

It’s no secret that some of the fundamentals of Cats like Monoid and Functor comes from category theory. Let’s try studying category theory and see if we can use the knowledge to further our understanding of Cats.

Basic category theory 

The most accessible category theory book I’ve come across is Lawvere and Schanuel’s Conceptual Mathematics: A First Introduction to Categories 2nd ed. The book mixes Articles, which is written like a normal textbook; and Sessions, which is kind of written like a recitation class.

Even in the Article section, Lawvere uses many pages to go over the basic concept compared to other books, which is good for self learners.

Sets, arrows, composition 

Lawvere:

Before giving a precise definition of ‘category’, we should become familiar with one example, the category of finite sets and maps. An object in this category is a finite set or collection. … You are probably familiar with some notations for finite sets:

{ John, Mary, Sam }

There are two ways that I can think of to express this in Scala. One is by using a value a: Set[Person]:

sealed trait Person {}
case object John extends Person {}
case object Mary extends Person {}
case object Sam extends Person {}

val a: Set[Person] = Set[Person](John, Mary, Sam)
// a: Set[Person] = Set(John, Mary, Sam)

Another way of looking at it, is that Person as the type is a finite set already without Set. Note: In Lawvere uses the term “map”, but I’m going to change to arrow like Mac Lane and others.

A arrow f in this cateogry consists of three things:

1. a set A, called the domain of the arrow,
2. a set B, called the codomain of the arrow,
3. a rule assigning to each element a in the domain, an element b in the codomain. This b is denoted by f ∘ a (or sometimes ’f(a)‘), read ’f of a‘.

(Other words for arrow are ‘function’, ‘transformation’, ‘operator’, ‘map’, and ‘morphism’.)

Let’s try implementing the favorite breakfast arrow.

sealed trait Breakfast {}
case object Eggs extends Breakfast {}
case object Oatmeal extends Breakfast {}
case object Toast extends Breakfast {}
case object Coffee extends Breakfast {}

lazy val favoriteBreakfast: Person => Breakfast = {
  case John => Eggs
  case Mary => Coffee
  case Sam  => Coffee
}

Note here that an “object” in this category is Set[Person] or Person, but the “arrow” favoriteBreakfast accepts a value whose type is Person. Here’s the internal diagram of the arrow.

The important thing is: For each dot in the domain, we have exactly one arrow leaving, and the arrow arrives at some dot in the codomain.

I get that a map can be more general than Function1[A, B] but it’s ok for this category. Here’s the implementation of favoritePerson:

lazy val favoritePerson: Person => Person = {
  case John => Mary
  case Mary => John
  case Sam  => Mary
}

An arrow in which the domain and codomain are the same object is called an endomorphism.

An arrow, in which the domain and codomain are the same set A, and for each of a in A, f(a) = a, is called an identity arrow.

The “identity arrow on A” is denoted as 1_A.

Again, identity is an arrow, so it works on an element in the set, not the set itself. So in this case we can just use scala.Predef.identity.

identity(John)
// res0: John.type = John

Here are the external diagrams corresponding to the three internal diagrams from the above.

This reiterates the point that in the category of finite sets, the “objects” translate to types like Person and Breakfast, and arrows translate to functions like Person => Person. The external diagram looks a lot like the type-level signatures like Person => Person.

The final basic ingredient, which is what lends all the dynamics to the notion of category is composition of arrows, by which two arrows are combined to obtain a third arrow.

We can do this in scala using scala.Function1’s andThen or compose.

lazy val favoritePersonsBreakfast = favoriteBreakfast compose favoritePerson

Here’s the internal diagram:

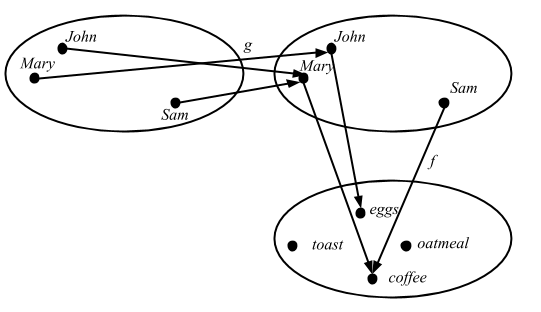
and the external diagram:

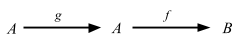
After composition the external diagram becomes as follows:

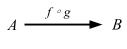
’f ∘ g’ is read ’f following g‘, or sometimes ’f of g‘.

Data for a category consists of the four ingredients:

• objects: A, B, C, …
• arrows: f: A => B
• identity arrows: 1_A: A => A
• composition of arrows

These data must satisfy the following rules:

The identity laws:

• If 1_A: A => A, g: A => B, then g ∘ 1_A = g
• If f: A => B, 1_B: B => B, then 1_A ∘ f = f

The associative law:

• If f: A => B, g: B => C, h: C => D, then h ∘ (g ∘ f) = (h ∘ g) ∘ f

Point 

Lawvere:

One very useful sort of set is a ‘singleton’ set, a set with exactly one element. Fix one of these, say {me}, and call this set ’1‘.

Definition: A point of a set X is an arrows 1 => X. … (If A is some familiar set, an arrow from A to X is called an ’A-element’ of X; thus ’1-elements’ are points.) Since a point is an arrow, we can compose it with another arrow, and get a point again.

If I understand what’s going on, it seems like Lawvere is redefining the concept of the element as a special case of arrow. Another name for singleton is unit set, and in Scala it is (): Unit. So it’s analogous to saying that values are sugar for Unit => X.

lazy val johnPoint: Unit => Person = { case () => John }
lazy val johnFav = favoriteBreakfast compose johnPoint

johnFav(())
// res1: Breakfast = Eggs

Session 2 and 3 contain nice review of Article I, so you should read them if you own the book.

Arrow 

As we saw, an arrow (or morphism) is a mapping between a domain and a codomain. Another way of thinking about it, is that its an abstract notion for things that behave like functions.

In Cats, an Arrow instance is provided for Function1[A, B], Kleisli[F[_], A, B], and Cokleisli[F[_], A, B].

Here’s the typeclass contract for Arrow:

package cats
package arrow

import cats.functor.Strong
import simulacrum.typeclass

@typeclass trait Arrow[F[_, _]] extends Split[F] with Strong[F] with Category[F] { self =>

  /**
   * Lift a function into the context of an Arrow
   */
  def lift[A, B](f: A => B): F[A, B]

  ....
}

Category 

Here’s the typeclass contract for Category:

package cats
package arrow

import simulacrum.typeclass

/**
 * Must obey the laws defined in cats.laws.CategoryLaws.
 */
@typeclass trait Category[F[_, _]] extends Compose[F] { self =>

  def id[A]: F[A, A]

  ....
}

Compose 

Here’s the typeclass contract for Compose:

package cats
package arrow

import simulacrum.typeclass

/**
 * Must obey the laws defined in cats.laws.ComposeLaws.
 */
@typeclass trait Compose[F[_, _]] { self =>

  @simulacrum.op("<<<", alias = true)
  def compose[A, B, C](f: F[B, C], g: F[A, B]): F[A, C]

  @simulacrum.op(">>>", alias = true)
  def andThen[A, B, C](f: F[A, B], g: F[B, C]): F[A, C] =
    compose(g, f)

  ....
}

This enables two operators <<< and >>>.

import cats._, cats.data._, cats.syntax.all._

lazy val f = (_:Int) + 1

lazy val g = (_:Int) * 100

(f >>> g)(2)
// res0: Int = 300

(f <<< g)(2)
// res1: Int = 201

Strong 

Let’s read Haskell’s Arrow tutorial:

First and second make a new arrow out of an existing arrow. They perform a transformation (given by their argument) on either the first or the second item of a pair. These definitions are arrow-specific.

Here’s Cat’s Strong:

package cats
package functor

import simulacrum.typeclass

/**
 * Must obey the laws defined in cats.laws.StrongLaws.
 */
@typeclass trait Strong[F[_, _]] extends Profunctor[F] {

  /**
   * Create a new `F` that takes two inputs, but only modifies the first input
   */
  def first[A, B, C](fa: F[A, B]): F[(A, C), (B, C)]

  /**
   * Create a new `F` that takes two inputs, but only modifies the second input
   */
  def second[A, B, C](fa: F[A, B]): F[(C, A), (C, B)]
}

This enables two methods first[C] and second[C].

lazy val f_first = f.first[Int]

f_first((1, 1))
// res2: (Int, Int) = (2, 1)

lazy val f_second = f.second[Int]

f_second((1, 1))
// res3: (Int, Int) = (1, 2)

Given that f here is a function to add one, I think it’s clear what f_first and f_second are doing.

Split 

(***) combines two arrows into a new arrow by running the two arrows on a pair of values (one arrow on the first item of the pair and one arrow on the second item of the pair).

This is called split in Cats.

package cats
package arrow

import simulacrum.typeclass

@typeclass trait Split[F[_, _]] extends Compose[F] { self =>

  /**
   * Create a new `F` that splits its input between `f` and `g`
   * and combines the output of each.
   */
  def split[A, B, C, D](f: F[A, B], g: F[C, D]): F[(A, C), (B, D)]
}

We can use it as split operator:

(f split g)((1, 1))
// res4: (Int, Int) = (2, 100)

Isomorphism 

Lawvere:

Definitions: An arrow f: A => B is called an isomorphism, or invertible arrow, if there is a map g: B => A, for which g ∘ f = 1_A and f ∘ g = 1_B. An arrow g related to f by satisfying these equations is called an inverse for f. Two objects A and B are said to be isomorphic if there is at least one isomorphism f: A => B.

Unfortunately, Cats doesn’t seem to have a datatype to represent isomorphisms, so we have to define one.

import cats._, cats.data._, cats.syntax.all._, cats.arrow.Arrow

object Isomorphisms {
  trait Isomorphism[Arrow[_, _], A, B] { self =>
    def to: Arrow[A, B]
    def from: Arrow[B, A]
  }
  type IsoSet[A, B] = Isomorphism[Function1, A, B]
  type <=>[A, B] = IsoSet[A, B]
}
import Isomorphisms._

This is now we can define an isomorphism from Family to Relic.

sealed trait Family {}
case object Mother extends Family {}
case object Father extends Family {}
case object Child extends Family {}

sealed trait Relic {}
case object Feather extends Relic {}
case object Stone extends Relic {}
case object Flower extends Relic {}

lazy val isoFamilyRelic = new (Family <=> Relic) {
  val to: Family => Relic = {
    case Mother => Feather
    case Father => Stone
    case Child  => Flower
  }
  val from: Relic => Family = {
    case Feather => Mother
    case Stone   => Father
    case Flower  => Child
  }
}

Equality of arrows 

To test this, we could first implement a test for comparing two functions. Two arrows are equal when they have the same three ingredients:

• domain A
• codomain B
• a rule that assigns f ∘ a

We can express this using ScalaCheck as follows:

scala> import org.scalacheck.{Prop, Arbitrary, Gen}
import org.scalacheck.{Prop, Arbitrary, Gen}

scala> import cats._, cats.data._, cats.syntax.all._
import cats._
import cats.data._
import cats.syntax.all._

scala> def func1EqualsProp[A, B](f: A => B, g: A => B)
         (implicit ev1: Eq[B], ev2: Arbitrary[A]): Prop =
         Prop.forAll { a: A =>
           f(a) === g(a)
         }
func1EqualsProp: [A, B](f: A => B, g: A => B)(implicit ev1: cats.Eq[B], implicit ev2: org.scalacheck.Arbitrary[A])org.scalacheck.Prop

scala> val p1 = func1EqualsProp((_: Int) + 2, 1 + (_: Int))
p1: org.scalacheck.Prop = Prop

scala> p1.check
! Falsified after 0 passed tests.
> ARG_0: 0

scala> val p2 = func1EqualsProp((_: Int) + 2, 2 + (_: Int))
p2: org.scalacheck.Prop = Prop

scala> p2.check
+ OK, passed 100 tests.

Testing for isomorphism 

scala> :paste
implicit val familyEqual = Eq.fromUniversalEquals[Family]
implicit val relicEqual = Eq.fromUniversalEquals[Relic]
implicit val arbFamily: Arbitrary[Family] = Arbitrary {
  Gen.oneOf(Mother, Father, Child)
}
implicit val arbRelic: Arbitrary[Relic] = Arbitrary {
  Gen.oneOf(Feather, Stone, Flower)
}

// Exiting paste mode, now interpreting.

familyEqual: cats.kernel.Eq[Family] = cats.kernel.Eq$$anon$116@99f2e3d
relicEqual: cats.kernel.Eq[Relic] = cats.kernel.Eq$$anon$116@159bd786
arbFamily: org.scalacheck.Arbitrary[Family] = org.scalacheck.ArbitraryLowPriority$$anon$1@799b3915
arbRelic: org.scalacheck.Arbitrary[Relic] = org.scalacheck.ArbitraryLowPriority$$anon$1@36c230c0

scala> func1EqualsProp(isoFamilyRelic.from compose isoFamilyRelic.to, identity[Family] _).check
+ OK, passed 100 tests.

scala> func1EqualsProp(isoFamilyRelic.to compose isoFamilyRelic.from, identity[Relic] _).check
+ OK, passed 100 tests.

This shows that the test was successful. That’s it for today.

day 16 

On day 15 we started looking at basic concepts in category theory using Lawvere and Schanuel’s Conceptual Mathematics. The book is a good introduction book into the notion of category because it spends a lot of pages explaining the basic concepts using concrete examples. The very aspect gets a bit tedious when you want to move on to more advanced concept, since it’s goes winding around.

Awodey’s ‘Category Theory‘ 

Today I’m switching to Steve Awodey’s Category Theory. This is also a book written for non-mathematicians, but goes at faster pace, and more emphasis is placed on thinking in abstract terms.

A definition or a theorem is called abstract, when it relies only on category theoric notions, rather than some additional information about the objects and arrows. The advantage of an abstract notion is that it applies in any category immediately.

Definition 1.3 In any category C, an arrow f: A => B is called an isomorphism, if there is an arrow g: B => A in C such that:

g ∘ f = 1_A and f ∘ g = 1_B.

Awodey names the above definition to be an abstract notion as it does make use only of category theoric notion.

Milewski’s ‘Category Theory for Programmers‘ 

Another good book to read together is Bartosz Milewski (@bartoszmilewski)’s Category Theory for Programmers that he’s been writing online.

Sets 

Before we go abtract, we’re going to look at some concrete categories. This is actually a good thing, since we only saw one category yesterday.

The category of sets and total functions are denoted by Sets written in bold. In Scala, this can be encoded roughly as types and functions between them, such as Int => String. There’s apprently a philosophical debate on whether it is correct because programming languages admit bottom type (Nothing), exceptions, and non-terminating code. For the sake of convenience, I’m happy to ignore it for now and pretend we can encode Sets.

Sets_fin 

The category of all finite sets and total functions between them are called Sets_fin.

Pos 

Awodey:

Another kind of example one often sees in mathematics is categories of structured sets, that is, sets with some further “structure” and functions that “preserve it,” where these notions are determined in some independent way.

A partially ordered set or poset is a set A equipped with a binary relation a ≤_A b such that the following conditions hold for all a, b, c ∈ A:

• reflexivity: a ≤_A a
• transitivity: if a ≤_A b and b ≤_A c, then a ≤_A c
• antisymmetry: if a ≤_A b and b ≤_A a, then a = b

An arrow from a poset A to a poset B is a function m: A => B that is monotone, in the sense that, for all a, a’ ∈ A,

• a ≤_A a’ implies m(a) ≤_A m(a’).

As long as the functions are monotone, the objects will continue to be in the category, so the “structure” is preserved. The category of posets and monotone functions is denoted as Pos. Awodey likes posets, so it’s important we understand it.

An example of poset is the Int type where the binary operation of ≤ is integer <= just as it is defined with PartialOrder typeclass. Another example could be case class LString(value: String) where ≤ is defined by comparing the length of value.

scala> :paste
// Entering paste mode (ctrl-D to finish)

case class LString(value: String)
val f: Int => LString = (x: Int) => LString(if (x < 0) "" else x.toString)

// Exiting paste mode, now interpreting.

defined class LString
f: Int => LString = <function1>

scala> f(0)
res0: LString = LString(0)

scala> f(10)
res1: LString = LString(10)

f in the above is monotone since f(0) ≤ f(10), and any other pairs of Ints that are a <= a'.

Finite categories 

Awodey:

Of course, the objects of a category do not have to be sets, either. Here are some very simple examples:

• The category 1 looks like this:
  
  It has one object and its identity arrow, which we do not draw.
• The category 2 looks like this:
  
  It has two objects, their required identity arrows, and exactly one arrow between the objects.
• The category 3 looks like this:
  
  It has three objects, their required identity arrows, exactly one arrow from the first to the second object, exactly one arrow from the second to the third object, and exactly one arrow from the first to the third object (which is therefore the composite of the other two).
• The category 0 looks like this:
  
  
  It has no objects or arrows.

We don’t have a direct application for these categories, but it’s good to keep them in mind to expand our notion of categories, and also so we can use them to form other concepts.

Cat 

Awodey:

Definition 1.2. A functor
F: C => D
between categories C and D is a mapping of objects to objects and arrows to arrows, in such a way that.

• F(f: A => B) = F(f): F(A) => F(B)
• F(1_A) = 1_F(A)
• F(g ∘ f) = F(g) ∘ F(f)

That is, F, preserves domains and codomains, identity arrows, and composition.

Now we are talking. Functor is an arrow between two categories. Here’s the external diagram:

The fact that the positions of F(A), F(B), and F(C) are distorted is intentional. That’s what F is doing, slightly distorting the picture, but still preserving the composition.

This category of categories and functors is denoted as Cat.

Let me remind you of the typographical conventions. The italic uppercase A, B, and C represent objects (which in case of Sets corresponds to types like Int and String). On the other hand, the bold uppercase C and D represent categories. Categories can be all kinds of things, including the datatypes we’ve seen ealier like List[A]. So a functor F: C => D is not some function, it’s an arrow between two categories.

In that sense, the way programmers use the term Functor is an extremely limited variety of the functor where C is hardcoded to Sets.

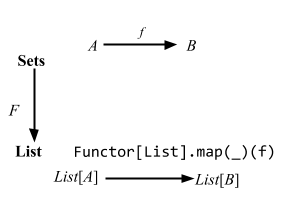
Monoid as categories 

Awodey:

A monoid (sometimes called a semigroup with unit) is a set M equipped with a binary operation ·: M × M => M and a distinguished “unit” element u ∈ M such that for all x, y, z ∈ M,

• x · (y · z) = (x · y) · z
• u · x = x = x · u

Equivalently, a monoid is a category with just one object. The arrows of the category are the elements of the monoid. In particular, the identity arrow is the unit element u. Composition of arrows is the binary operation m · n for the monoid.

See Monoid from day 4 for how Monoid is encoded in Cats.

trait Monoid[@sp(Int, Long, Float, Double) A] extends Any with Semigroup[A] {
  def empty: A

  ....
}

trait Semigroup[@sp(Int, Long, Float, Double) A] extends Any with Serializable {
  def combine(x: A, y: A): A

  ....
}

Here is addition of Int and 0:

scala> 10 |+| Monoid[Int].empty
res26: Int = 10

The idea that these monoids are categories with one object and that elements are arrows used to sound so alien to me, but now it’s a bit more understandable since we were exposed to singleton.

Note in the above monoid (Int, +), arrows are literally 0, 1, 2, etc, and that they are not functions.

Mon 

There’s another category related to monoids. The category of monoids and functions that preserve the monoid structure is denoted by Mon. These arrows that preserve structure are called homomorphism.

In detail, a homomorphism from a monoid M to a monoid N is a function h: M => N such that for all m, n ∈ M,

• h(m ·_M n) = h(m) ·_N h(n)
• h(u_M) = u_N

Since a monoid is a category, a monoid homomorphism is a special case of functors.

Grp 

Awodey:

Definition 1.4 A group G is a monoid with an inverse g^-1 for every element g. Thus, G is a category with one object, in which every arrow is an isomorphism.

Here’s the typeclass contract of cats.kernel.Monoid:

/**
 * A group is a monoid where each element has an inverse.
 */
trait Group[@sp(Int, Long, Float, Double) A] extends Any with Monoid[A] {

  /**
   * Find the inverse of `a`.
   *
   * `combine(a, inverse(a))` = `combine(inverse(a), a)` = `empty`.
   */
  def inverse(a: A): A
}

This enables inverse method if the syntax is imported.

import cats._, cats.syntax.all._

1.inverse
// res0: Int = -1

assert((1 |+| 1.inverse) === Monoid[Int].empty)

The category of groups and group homomorphism (functions that preserve the monoid structure) is denoted by Grp.

Forgetful functor 

We’ve seen the term homomorphism a few times, but it’s possible to think of a function that doesn’t preserve the structure. Because every group G is also a monoid we can think of a function f: G => M where f loses the inverse ability from G and returns underlying monoid as M. Since both groups and monoids are categories, f is a functor.

We can extend this to the entire Grp, and think of a functor F: Grp => Mon. These kinds of functors that strips the structure is called forgetful functors. If we try to express this using Scala, you would start with A: Group, and somehow downgrade to A: Monoid as the ruturn value.

That’s it for today.

day 17 

On day 16 we looked at some concrete categories using Awodey’s ‘Category Theory’ as the guide.

We can now talk about abstract structures today. A definition or a theorem is called abstract, when it relies only on category theoric notions, rather than some additional information about the objects and arrows. The definition of isomorphism is one such example:

Definition 1.3 In any category C, an arrow f: A => B is called an isomorphism, if there is an arrow g: B => A in C such that:

g ∘ f = 1_A and f ∘ g = 1_B.

We can use this notion of isomorphism as a building block to explore more concepts.

Initial and terminal objects 

When a definition relies only on category theoretical notion (objects and arrows), it often reduces down to a form “given a diagram abc, there exists a unique x that makes another diagram xyz commute.” Commutative in this case mean that all the arrows compose correctly. Such defenition is called a universal property or a universal mapping property (UMP).

Some of the notions have a counterpart in set theory, but it’s more powerful because of its abtract nature. Consider making the empty set and the one-element sets in Sets abstract.

Definition 2.9. In any category C, an object

• 0 is initial if for any object C there is a unique morphism
  
• 1 is terminal if for any object C there is a unique morphism
  

The two diagrams look almost too simple to understand, but the definitions are examples of UMP. The first one is saying that given the diagram, and so if 0 exists, the arrow 0 => C is unique.

Uniquely determined up to isomorphism 

As a general rule, the uniqueness requirements of universal mapping properties are required only up to isomorphisms. Another way of looking at it is that if objects A and B are isomorphic to each other, they are “equal in some sense.” To signify this, we write A ≅ B.

Proposition 2.10 Initial (terminal) objects are unique up to isomorphism.
Proof. In fact, if C and C’ are both initial (terminal) in the same category, then there’s a unique isomorphism C => C’. Indeed, suppose that 0 and 0’ are both initial objects in some category C; the following diagram then makes it clear that 0 and 0’ are uniquely isomorphic:

Given that isomorphism is defined by g ∘ f = 1_A and f ∘ g = 1_B, this looks good.

Examples of initial objects 

An interest aspect of abstract construction is that they can show up in different categories in different forms.

In Sets, the empty set is initial and any singleton set {x} is terminal.

Recall that we can encode Set using types and functions between them. In Scala, the uninhabited type might be Nothing, so we’re saying that there is only one function between Nothing to A. According to Milewski, there’s a function in Haskell called absurd. Our implementation might look like this:

def absurd[A]: Nothing => A = { case _ => ??? }

absurd[Int]
// res0: Function1[Nothing, Int] = <function1>

Given that there’s no value in the domain of the function, the body should never be executed.

In a poset, an object is plainly initial iff it is the least element, and terminal iff it is the greatest element.

This kind of makes sense, since in a poset we need to preserve the structure using ≤.

Examples of terminal objects 

A singleton set means it’s a type that has only one possible value. An example of that in Scala would be Unit. There can be only one possible implementation from general A to Unit:

def unit[A](a: A): Unit = ()

unit(1)

This makes Unit a terminal object in the category of Sets, but note that we can define singleton types all we want in Scala using object:

case object Single
def single[A](a: A): Single.type = Single

single("test")
// res2: Single.type = Single

As noted above, in a poset, an object is terminal iff it is the greatest element.

Product 

Let us begin by considering products of sets. Given sets A and B, the cartesian product of A and B is the set of ordered pairs
A × B = {(a, b)| a ∈ A, b ∈ B}

There are two coordinate projections:

with:

• fst ∘ (a, b) = a
• snd ∘ (a, b) = b

This notion of product relates to scala.Product, which is the base trait for all tuples and case classes.

For any element in c ∈ A × B, we have c = (fst ∘ c, snd ∘ c)

If we recall from day 15, we can generalize the concept of elements by introducing the singleton 1 explicitly.

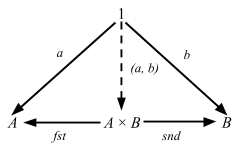
If we clean it up a bit more, we get the following categorical definition of a product:

Definition 2.15. In any category C, a product diagram for the objects A and B consists of an object P and arrows p₁ and p₂

satisfying the following UMP:

Given any diagram of the form

there exists a unique u: X => P, making the diagram

commute, that is, such that x₁ = p₁ u and x₂ = p₂ u.

“There exists unique u” is a giveaway that this definition is an UMP.

Uniqueness of products 

If we step back to Sets, all it’s saying is that given type A and type B, there’s a unique function that can return (A, B). But how can we prove that for all categories? All we have at our disposal are alphabets and arrows.

Proposition 2.17 Products are unique up to isomorphism.

Suppose we have P and Q that are products of objects A and B.

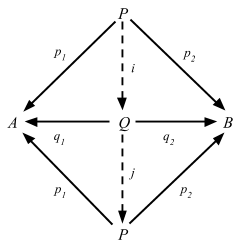
1. Because P is a product, there is a unique i: P => Q such that p₁ = q₁ ∘ i and p₂ = q₂ ∘ i
2. Because Q is a product, there is a unique j: Q => P such that q₁ = p₁ ∘ j and q₂ = p₂ ∘ j
3. By composing j and i we get 1_P = j ∘ i
4. Similarly, we can also get 1_Q = i ∘ j
5. Thus i is an isomorphism, and P ≅ Q ∎

Since all products are isometric, we can just denote one as A × B, and the arrow u: X => A × B is denoted as ⟨x₁, x₂⟩.

Duality 

Opposite category 

Before we get into duality, we need to cover the concept of generating a category out of an existing one. Note that we are no longer talking about objects, but a category, which includes objects and arrows.

The opposite (or “dual”) category C^op of a category C has the same objects as C, and an arrow f: C => D in C^op is an arrow f: D => C in C. That is, C^op is just C with all of the arrows formally turned around.

The duality principle 

If we take the concept further, we can come up with “dual statement” Σ^* by substituting any sentence Σ in the category theory by replacing the following:

• f ∘ g for g ∘ f
• codomain for domain
• domain for codomain

Since there’s nothing semantically important about which side is f or g, the dual statement also holds true as long as Σ only relies on category theory. In other words, any proof that holds for one concept also holds for its dual. This is called the duality principle.

Another way of looking at it is that if Σ holds in all C, it should also hold in C^op, and so Σ^* should hold in (C^op)^op, which is C.

Let’s look at the definitions of initial and terminal again:

Definition 2.9. In any category C, an object

• 0 is initial if for any object C there is a unique morphism
  0 => C
• 1 is terminal if for any object C there is a unique morphism
  C => 1

They are dual to each other, so the initials in C are terminals in C^op.

Recall proof for “the initial objects are unique up to isomorphism.”

If you flip the direction of all arrows in the above diagram, you do get a proof for terminals.

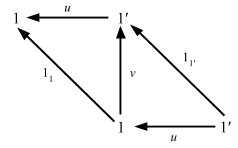
This is pretty cool.

Coproduct 

One of the well known duals is coproduct, which is the dual of product. Prefixing with “co-” is the convention to name duals.

Here’s the definition of products again:

Definition 2.15. In any category C, a product diagram for the objects A and B consists of an object P and arrows p₁ and p₂

satisfying the following UMP:

Given any diagram of the form

there exists a unique u: X => P, making the diagram

commute, that is, such that x₁ = p₁ u and x₂ = p₂ u.

Flip the arrows around, and we get a coproduct diagram:

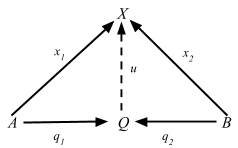
Since coproducts are unique up to isomorphism, we can denote the coproduct as A + B, and [f, g] for the arrow u: A + B => X.

The “coprojections” i₁: A => A + B and i₂: B => A + B are usually called injections, even though they need not be “injective” in any sense.

Similar to the way products related to product type encoded as scala.Product, coproducts relate to the notion of sum type, or disjoint union type.

Algebraic datatype 

First way to encode A + B might be using sealed trait and case classes.

sealed trait XList[A]

object XList {
  case class XNil[A]() extends XList[A]
  case class XCons[A](head: A, rest: XList[A]) extends XList[A]
}

XList.XCons(1, XList.XNil[Int])
// res0: XList.XCons[Int] = XCons(head = 1, rest = XNil())

Either datatype as coproduct 

If we squint Either can be considered a union type. We can define a type alias called |: for Either as follows:

type |:[+A1, +A2] = Either[A1, A2]

Because Scala allows infix syntax for type constructors, we can write Either[String, Int] as String |: Int.

val x: String |: Int = Right(1)
// x: String |: Int = Right(value = 1)

Thus far I’ve only used normal Scala features only. Cats provides a typeclass called cats.Inject that represents injections i₁: A => A + B and i₂: B => A + B. You can use it to build up a coproduct without worrying about Left or Right.

import cats._, cats.data._, cats.syntax.all._

val a = Inject[String, String |: Int].inj("a")
// a: String |: Int = Left(value = "a")

val one = Inject[Int, String |: Int].inj(1)
// one: String |: Int = Right(value = 1)

To retrieve the value back you can call prj:

Inject[String, String |: Int].prj(a)
// res1: Option[String] = Some(value = "a")

Inject[String, String |: Int].prj(one)
// res2: Option[String] = None

We can also make it look nice by using apply and unapply:

lazy val StringInj = Inject[String, String |: Int]

lazy val IntInj = Inject[Int, String |: Int]

val b = StringInj("b")
// b: String |: Int = Left(value = "b")

val two = IntInj(2)
// two: String |: Int = Right(value = 2)

two match {
  case StringInj(x) => x
  case IntInj(x)    => x.show + "!"
}
// res3: String = "2!"

The reason I put colon in |: is to make it right-associative. This matters when you expand to three types:

val three = Inject[Int, String |: Int |: Boolean].inj(3)
// three: String |: Int |: Boolean = Right(value = Left(value = 3))

The return type is String |: (Int |: Boolean).

Curry-Howard encoding 

An interesting read on this topic is Miles Sabin (@milessabin)’s Unboxed union types in Scala via the Curry-Howard isomorphism.

Shapeless.Coproduct 

See also Coproducts and discriminated unions in Shapeless.

EitherK datatype 

There’s a datatype in Cats called EitherK[F[_], G[_], A], which is an either on type constructor.

In Data types à la carte Wouter Swierstra (@wouterswierstra) describes how this could be used to solve the so-called Expression Problem.

That’s it for today.

day 18 

On day 17 we looked at some abstract structures such as initial and terminal objects, product, and duality using Awodey’s ‘Category Theory’ as the guide.

Daniel Steger for openphoto.net

Effect system 

In Lazy Functional State Threads, John Launchbury and Simon Peyton-Jones write:

Based on earlier work on monads, we present a way of securely encapsulating stateful computations that manipulate multiple, named, mutable objects, in the context of a non-strict purely-functional language.

Because Scala has vars, at first it seems pointless to encapusulate mutation, but the concept of abstracting over stateful computation can be useful. Under some circumstances like parallel execution, it’s critical that states are either not shared or shared with care.

Cats Effect and Monix both provide effect system for the Cats ecosystem. Let’s try looking at Cats Effect using “State Threads” paper as the guide.

Cats Effect sbt setup 

val catsEffectVersion = "3.0.2"
val http4sVersion = "1.0.0-M21"

val catsEffect = "org.typelevel" %% "cats-effect" % catsEffectVersion
val http4sBlazeClient = "org.http4s" %% "http4s-blaze-client" % http4sVersion
val http4sCirce = "org.http4s" %% "http4s-circe" % http4sVersion

Ref 

LFST:

What is a “state”? Part of every state is a finite mapping from reference to values. … A reference can be thought of as the name of (or address of) a variable, an updatable location in the state capable of holding a value.

Ref is a thread-safe mutable variable that’s used in the context of Cats Effect’s IO monad.

Ref says:

Ref provides safe concurrent access and modification of its content, but no functionality for synchronisation.

trait RefSource[F[_], A] {

  /**
   * Obtains the current value.
   *
   * Since `Ref` is always guaranteed to have a value, the returned action
   * completes immediately after being bound.
   */
  def get: F[A]
}

trait RefSink[F[_], A] {

  /**
   * Sets the current value to `a`.
   *
   * The returned action completes after the reference has been successfully set.
   *
   * Satisfies:
   *   `r.set(fa) *> r.get == fa`
   */
  def set(a: A): F[Unit]
}

abstract class Ref[F[_], A] extends RefSource[F, A] with RefSink[F, A] {
  /**
   * Modifies the current value using the supplied update function. If another modification
   * occurs between the time the current value is read and subsequently updated, the modification
   * is retried using the new value. Hence, `f` may be invoked multiple times.
   *
   * Satisfies:
   *   `r.update(_ => a) == r.set(a)`
   */
  def update(f: A => A): F[Unit]

  def modify[B](f: A => (A, B)): F[B]

  ....
}

Here’s how we can use this:

import cats._, cats.syntax.all._
import cats.effect.{ IO, Ref }

def e1: IO[Ref[IO, Int]] = for {
  r <- Ref[IO].of(0)
  _ <- r.update(_ + 1)
} yield r

def e2: IO[Int] = for {
  r <- e1
  x <- r.get
} yield x

{
  import cats.effect.unsafe.implicits._
  e2.unsafeRunSync()
}
// res0: Int = 1

e1 creates a new reference with 0, and updates it by adding 1. e2 composes e1 and retrieves the internal value. Finally, unsafeRunSync() is called to run the effect.

IO datatype 

Analoguous to Launchbury and SPJ’s “State Threads” paper, Cats Effect uses the notion of lightweight thread called fibers to model the effects.

sealed abstract class IO[+A] private () extends IOPlatform[A] {

  def flatMap[B](f: A => IO[B]): IO[B] = IO.FlatMap(this, f)

  ....


  // from IOPlatform
  final def unsafeRunSync()(implicit runtime: unsafe.IORuntime): A
}

object IO extends IOCompanionPlatform with IOLowPriorityImplicits {
  /**
   * Suspends a synchronous side effect in `IO`.
   *
   * Alias for `IO.delay(body)`.
   */
  def apply[A](thunk: => A): IO[A] = Delay(() => thunk)

  def delay[A](thunk: => A): IO[A] = apply(thunk)

  def async[A](k: (Either[Throwable, A] => Unit) => IO[Option[IO[Unit]]]): IO[A] =
    asyncForIO.async(k)

  def async_[A](k: (Either[Throwable, A] => Unit) => Unit): IO[A] =
    asyncForIO.async_(k)

  def canceled: IO[Unit] = Canceled

  def cede: IO[Unit] = Cede

  def sleep(delay: FiniteDuration): IO[Unit] =
    Sleep(delay)

  def race[A, B](left: IO[A], right: IO[B]): IO[Either[A, B]] =
    asyncForIO.race(left, right)

  def readLine: IO[String] =
    Console[IO].readLine

  def print[A](a: A)(implicit S: Show[A] = Show.fromToString[A]): IO[Unit] =
    Console[IO].print(a)

  def println[A](a: A)(implicit S: Show[A] = Show.fromToString[A]): IO[Unit] =
    Console[IO].println(a)

  def blocking[A](thunk: => A): IO[A] =
    Blocking(TypeBlocking, () => thunk)

  def interruptible[A](many: Boolean)(thunk: => A): IO[A] =
    Blocking(if (many) TypeInterruptibleMany else TypeInterruptibleOnce, () => thunk)

  def suspend[A](hint: Sync.Type)(thunk: => A): IO[A] =
    if (hint eq TypeDelay)
      apply(thunk)
    else
      Blocking(hint, () => thunk)

  ....
}

Hello world 

Here’s a hello world program using Cats Effect IO.

package example

import cats._, cats.syntax.all._
import cats.effect.IO

object Hello extends App {
  val program = for {
    _ <- IO.print("What's your name? ")
    x <- IO.readLine
    _ <- IO.println(s"Hello, $x")
  } yield ()
}

Running this looks like this:

> run
[info] running example.Hello
[success] Total time: 1 s, completed Apr 11, 2021 12:51:44 PM

Nothing should have happened. Unlike standard library’s scala.concurrent.Future + standard execution contexts, IO datatype represents an effect in a suspended state, and it does not execute until we tell it to run explicitly.

Here’s how we can run it:

package example

import cats._, cats.syntax.all._
import cats.effect.IO

object Hello extends App {
  val program = for {
    _ <- IO.print("What's your name? ")
    x <- IO.readLine
    _ <- IO.println(s"Hello, $x")
  } yield ()

  import cats.effect.unsafe.implicits.global
  program.unsafeRunSync()
}

Now we’ll see the side effects:

sbt:herding-cats> run
[info] running example.Hello
What's your name? eugene
Hello, eugene
[success] Total time: 4 s, completed Apr 11, 2021 1:00:19 PM

Cats Effect comes with a better program harness called IOApp, which you should use for actual program:

import cats._, cats.syntax.all._
import cats.effect.{ ExitCode, IO, IOApp }

object Hello extends IOApp {
  override def run(args: List[String]): IO[ExitCode] =
    program.as(ExitCode.Success)

  lazy val program = for {
    _ <- IO.print("What's your name? ")
    x <- IO.readLine
    _ <- IO.println(s"Hello, $x")
  } yield ()
}

These examples show that IO datatype can compose monadically, but they are executing sequentially.

Pizza app 

To motivate the use of IO, let’s consider a pizza app using http4s client.

import cats._, cats.syntax.all._
import cats.effect.IO
import org.http4s.client.Client

def withHttpClient[A](f: Client[IO] => IO[A]): IO[A] = {
  import java.util.concurrent.Executors
  import scala.concurrent.ExecutionContext
  import org.http4s.client.blaze.BlazeClientBuilder
  val threadPool = Executors.newFixedThreadPool(5)
  val httpEc = ExecutionContext.fromExecutor(threadPool)
  BlazeClientBuilder[IO](httpEc).resource.use(f)
}

def search(httpClient: Client[IO], q: String): IO[String] = {
  import io.circe.Json
  import org.http4s.Uri
  import org.http4s.circe._
  val baseUri = Uri.unsafeFromString("https://api.duckduckgo.com/")
  val target = baseUri
    .withQueryParam("q", q + " pizza")
    .withQueryParam("format", "json")
  httpClient.expect[Json](target) map { json =>
    json.findAllByKey("Abstract").headOption.flatMap(_.asString).getOrElse("")
  }
}

{
  import cats.effect.unsafe.implicits.global
  val program = withHttpClient { httpClient =>
    search(httpClient, "New York")
  }
  program.unsafeRunSync()
}
// res0: String = "New York\u2013style pizza is pizza made with a characteristically large hand-tossed thin crust, often sold in wide slices to go. The crust is thick and crisp only along its edge, yet soft, thin, and pliable enough beneath its toppings to be folded in half to eat. Traditional toppings are simply tomato sauce and shredded mozzarella cheese. This style evolved in the U.S. from the pizza that originated in New York City in the early 1900s, itself derived from the Neapolitan-style pizza made in Italy. Today it is the dominant style eaten in the New York Metropolitan Area states of New York, and New Jersey and variously popular throughout the United States. Regional variations exist throughout the Northeast and elsewhere in the U.S."

This constructs a program that queries Duck Duck Go API about New York style pizza. To mitigate the latency involved in the network IO, we’d like to make parallel calls:

{
  import cats.effect.unsafe.implicits.global
  val program = withHttpClient { httpClient =>
    val xs = List("New York", "Neapolitan", "Sicilian", "Chicago", "Detroit", "London")
    xs.parTraverse(search(httpClient, _))
  }
  program.unsafeRunSync()
}
// res1: List[String] = List(
//   "New York\u2013style pizza is pizza made with a characteristically large hand-tossed thin crust, often sold in wide slices to go. The crust is thick and crisp only along its edge, yet soft, thin, and pliable enough beneath its toppings to be folded in half to eat. Traditional toppings are simply tomato sauce and shredded mozzarella cheese. This style evolved in the U.S. from the pizza that originated in New York City in the early 1900s, itself derived from the Neapolitan-style pizza made in Italy. Today it is the dominant style eaten in the New York Metropolitan Area states of New York, and New Jersey and variously popular throughout the United States. Regional variations exist throughout the Northeast and elsewhere in the U.S.",
//   "Neapolitan pizza also known as Naples-style pizza, is a style of pizza made with tomatoes and mozzarella cheese. It must be made with either San Marzano tomatoes or Pomodorino del Piennolo del Vesuvio, which grow on the volcanic plains to the south of Mount Vesuvius, and Mozzarella di Bufala Campana, a protected designation of origin cheese made with the milk from water buffalo raised in the marshlands of Campania and Lazio in a semi-wild state, or \"Mozzarella STG\", a cow's milk mozzarella. Neapolitan pizza is a Traditional Speciality Guaranteed product in Europe, and the art of its making is included on UNESCO's list of intangible cultural heritage. This style of pizza gave rise to the New York-style pizza that was first made by Italian immigrants to the United States in the early 20th century.",
//   "Sicilian pizza is pizza prepared in a manner that originated in Sicily, Italy. Sicilian pizza is also known as sfincione or focaccia with toppings. This type of pizza became a popular dish in western Sicily by the mid-19th century and was the type of pizza usually consumed in Sicily until the 1860s. The version with tomatoes was not available prior to the 17th century. It eventually reached North America in a slightly altered form, with thicker crust and a rectangular shape. Traditional Sicilian pizza is often thick crusted and rectangular, but can also be round and similar to the Neapolitan pizza. It is often topped with onions, anchovies, tomatoes, herbs and strong cheese such as caciocavallo and toma. Other versions do not include cheese. The Sicilian methods of making pizza are linked to local culture and country traditions, so there are differences in preparing pizza among the Sicilian regions of Palermo, Catania, Siracusa and Messina.",
//   "Chicago-style pizza is pizza prepared according to several different styles developed in Chicago. The most famous is the deep-dish pizza. The pan in which it is baked gives the pizza its characteristically high edge which provides ample space for large amounts of cheese and a chunky tomato sauce. Chicago-style pizza may be prepared in deep-dish style and as a stuffed pizza.",
//   "Detroit-style pizza is a rectangular pizza with a thick crust that is crispy and chewy. It is traditionally topped with tomato sauce and Wisconsin brick cheese that goes all the way to the edges. This style of pizza is often baked in rectangular steel trays designed for use as automotive drip pans or to hold small industrial parts in factories. The style was developed during the mid-twentieth century in Detroit before spreading to other parts of the United States in the 2010s. The dish is one of Detroit's iconic local foods.",
//   ""
// )

.parTraverse(...) internally spawns fibers so the IO actions would be performed in parallel. Now that we have parallel IOs, we can try using Ref again to excercise the thread-safety of Ref.

import cats.effect.Ref

def appendCharCount(httpClient: Client[IO], q: String, ref: Ref[IO, List[(String, Int)]]): IO[Unit] =
  for {
    s <- search(httpClient, q)
    _ <- ref.update(((q, s.size)) :: _)
  } yield ()

{
  import cats.effect.unsafe.implicits.global
  val program = withHttpClient { httpClient =>
    val xs = List("New York", "Neapolitan", "Sicilian", "Chicago", "Detroit", "London")

    for {
      r <- Ref[IO].of(Nil: List[(String, Int)])
      _ <- xs.parTraverse(appendCharCount(httpClient, _, r))
      x <- r.get
    } yield x
  }
  program.unsafeRunSync().reverse
}
// res2: List[(String, Int)] = List(
//   ("Sicilian", 954),
//   ("Detroit", 530),
//   ("Chicago", 376),
//   ("London", 0),
//   ("Neapolitan", 806),
//   ("New York", 731)
// )

Here we’re combining sequential and parallel composition of the IO effects.

ApplicativeError 

In Scala there are multiple ways to reprent the error state. Cats provides ApplicativeError typeclass to represent raising and recovering from an error.

trait ApplicativeError[F[_], E] extends Applicative[F] {
  def raiseError[A](e: E): F[A]

  def handleErrorWith[A](fa: F[A])(f: E => F[A]): F[A]


  def recover[A](fa: F[A])(pf: PartialFunction[E, A]): F[A] =
    handleErrorWith(fa)(e => (pf.andThen(pure(_))).applyOrElse(e, raiseError[A](_)))
  def recoverWith[A](fa: F[A])(pf: PartialFunction[E, F[A]]): F[A] =
    handleErrorWith(fa)(e => pf.applyOrElse(e, raiseError))
}

Either as ApplicativeError 

import cats._, cats.syntax.all._

{
  val F = ApplicativeError[Either[String, *], String]
  F.raiseError("boom")
}
// res0: Either[String, Nothing] = Left(value = "boom")

{
  val F = ApplicativeError[Either[String, *], String]
  val e = F.raiseError("boom")
  F.recover(e) {
    case "boom" => 1
  }
}
// res1: Either[String, Int] = Right(value = 1)

An interesting thing to note is that unlike try-catch, where the type switches between the error type Throwable and the happy type A, ApplicativeError needs to hold on to both E and A as data.

scala.util.Try as ApplicativeError 

import scala.util.Try

{
  val F = ApplicativeError[Try, Throwable]
  F.raiseError(new RuntimeException("boom"))
}
// res2: Try[Nothing] = Failure(exception = java.lang.RuntimeException: boom)

{
  val F = ApplicativeError[Try, Throwable]
  val e = F.raiseError(new RuntimeException("boom"))
  F.recover(e) {
    case _: Throwable => 1
  }
}
// res3: Try[Int] = Success(value = 1)

IO as ApplicativeError 

Given that IO needs to run inside of a fiber, it has the ability to capture the error state similar to scala.util.Try and Future.

import cats.effect.IO

{
  val F = ApplicativeError[IO, Throwable]
  F.raiseError(new RuntimeException("boom"))
}
// res4: IO[Nothing] = Error(t = java.lang.RuntimeException: boom)

{
  val F = ApplicativeError[IO, Throwable]
  val e = F.raiseError(new RuntimeException("boom"))
  val io: IO[Int] = F.recover(e) {
    case _: Throwable => 1
  }
}

MonadCancel 

An interesting thing about Cats Effect is that it is as much a library providing typeclasses for functional effect as much as it is an implementation of Ref, IO and other datatypes.

MonadCancel is a fundamental typeclass extending MonadError (Monad extension of ApplicativeError) supporting safe cancelation, masking, and finalization. We can think of this as functional construct for try-catch-finally.

trait MonadCancel[F[_], E] extends MonadError[F, E] {
  def rootCancelScope: CancelScope

  def forceR[A, B](fa: F[A])(fb: F[B]): F[B]

  def uncancelable[A](body: Poll[F] => F[A]): F[A]

  def canceled: F[Unit]

  def onCancel[A](fa: F[A], fin: F[Unit]): F[A]

  def bracket[A, B](acquire: F[A])(use: A => F[B])(release: A => F[Unit]): F[B] =
    bracketCase(acquire)(use)((a, _) => release(a))

  def bracketCase[A, B](acquire: F[A])(use: A => F[B])(
      release: (A, Outcome[F, E, B]) => F[Unit]): F[B] =
    bracketFull(_ => acquire)(use)(release)

  def bracketFull[A, B](acquire: Poll[F] => F[A])(use: A => F[B])(
      release: (A, Outcome[F, E, B]) => F[Unit]): F[B]
}

IO as MonadCancel 

MonadCancel documentation says:

One particularly unique aspect of MonadCancel is the ability to self-cancel.

import cats._, cats.syntax.all._
import cats.effect.IO

lazy val program = IO.canceled >> IO.println("nope")

scala> {
         import cats.effect.unsafe.implicits.global
         program.unsafeRunSync()
       }
java.util.concurrent.CancellationException: Main fiber was canceled
  at cats.effect.IO.$anonfun$unsafeRunAsync$1(IO.scala:640)
  at cats.effect.IO.$anonfun$unsafeRunFiber$2(IO.scala:702)
  at scala.runtime.java8.JFunction0$mcV$sp.apply(JFunction0$mcV$sp.scala:18)
  at cats.effect.kernel.Outcome.fold(Outcome.scala:37)
  at cats.effect.kernel.Outcome.fold$(Outcome.scala:35)
  at cats.effect.kernel.Outcome$Canceled.fold(Outcome.scala:181)
  at cats.effect.IO.$anonfun$unsafeRunFiber$1(IO.scala:708)
  at cats.effect.IO.$anonfun$unsafeRunFiber$1$adapted(IO.scala:698)
  at cats.effect.CallbackStack.apply(CallbackStack.scala:45)
  at cats.effect.IOFiber.done(IOFiber.scala:894)
  at cats.effect.IOFiber.asyncCancel(IOFiber.scala:941)
  at cats.effect.IOFiber.runLoop(IOFiber.scala:458)
  at cats.effect.IOFiber.execR(IOFiber.scala:1117)
  at cats.effect.IOFiber.run(IOFiber.scala:125)
  at cats.effect.unsafe.WorkerThread.run(WorkerThread.scala:358)

Here’s a less dramatic one:

{
  import cats.effect.unsafe.implicits.global
  program.unsafeRunAndForget()
}

Either case, the effect is canceled, and "nope" action does not take place.

Note that the idea of cancellation is also scripted inside of the IO datatype. This is contrasting to Monix Task where the cancellation happens against CancelableFuture, after the end of the world so to speak.

F.uncancelable 

Since cancellation can be inconvenient at certain timings, MonadCancel actually provides a uncancelable region, which can be used like this:

lazy val program2 = IO.uncancelable { _ =>
  IO.canceled >> IO.println("important")
}

scala> {
         import cats.effect.unsafe.implicits.global
         program2.unsafeRunSync()
       }
important

Within IO.uncancelable { ... }, cancellation is ignored. To opt back into the cancellation, you can used the passed in poll function:

lazy val program3 = IO.uncancelable { poll =>
  poll(IO.canceled) >> IO.println("nope again")
}

scala> {
         import cats.effect.unsafe.implicits.global
         program3.unsafeRunSync()
       }
java.util.concurrent.CancellationException: Main fiber was canceled
  ....

IO.uncancelable { ... } regions are low-level API, and not likely to be used directly.

bracket 

MonadCancel documentation says:

This means that when writing resource-safe code, we have to worry about cancelation as well as exceptions.

import cats.effect.MonadCancel

lazy val program4 = MonadCancel[IO].bracket(IO.pure(0))(x =>
  IO.raiseError(new RuntimeException("boom")))(_ =>
    IO.println("cleanup"))

scala> {
         import cats.effect.unsafe.implicits.global
         program4.unsafeRunSync()
       }
cleanup
java.lang.RuntimeException: boom
  ....

Using MonadCancel[IO].bracket we can guarantee that the cleanup code will run.

That’s it for today.

day 19 

On day 18 we started looking into Cats Effect as an example of effect system, while glancing at John Launchbury and Simon Peyton-Jones’s Lazy Functional State Threads.

We saw that IO datatype is able to describe a program that can be composed in either sequential and parallel way.

FunctionK 

Cats provides FunctionK that accepts two type constructors F1[_] and F2[_] as type parameter that can transform all values in F1[A] to F2[A] for all A.

trait FunctionK[F[_], G[_]] extends Serializable { self =>

  /**
   * Applies this functor transformation from `F` to `G`
   */
  def apply[A](fa: F[A]): G[A]

  def compose[E[_]](f: FunctionK[E, F]): FunctionK[E, G] =
    new FunctionK[E, G] { def apply[A](fa: E[A]): G[A] = self(f(fa)) }

  def andThen[H[_]](f: FunctionK[G, H]): FunctionK[F, H] =
    f.compose(self)

  def or[H[_]](h: FunctionK[H, G]): FunctionK[EitherK[F, H, *], G] =
    new FunctionK[EitherK[F, H, *], G] { def apply[A](fa: EitherK[F, H, A]): G[A] = fa.fold(self, h) }

  ....
}

FunctionK[F1, F2] is denoted symbolically as F1 ~> F2:

import cats._, cats.syntax.all._

lazy val first: List ~> Option = ???

Because we tend to call F[_] as functors, sometimes FunctionK is aspirationally called a natural transformation, but I think FunctionK is a better name for what it does.

Let’s try implementing List ~> Option that returns the first element.

val first: List ~> Option = new (List ~> Option) {
  def apply[A](fa: List[A]): Option[A] = fa.headOption
}
// first: List ~> Option = repl.MdocSession1@331e0beb

first(List("a", "b", "c"))
// res1: Option[String] = Some(value = "a")

It looks a bit verbose. Depending on how often this shows up in the code, we might want a way to write it shorter like how we’re usually able to write:

import scala.util.chaining._

List("a", "b", "c").pipe(_.headOption)
// res2: Option[String] = Some(value = "a")

We can do this using polymorphic lambda rewrite λ provided by the kind projector:

val first = λ[List ~> Option](_.headOption)
// first: AnyRef with List ~> Option = repl.MdocSession2@16c1db63

first(List("a", "b", "c"))
// res4: Option[String] = Some(value = "a")

Higher-Rank Polymorphism in Scala 

In July of 2010, Rúnar (@runarorama) wrote a blog post Higher-Rank Polymorphism in Scala, describing the concept of rank-2 polymorphism. First, here’s an ordinary (rank-1) polymorphic function:

def pureList[A](a: A): List[A] = List(a)

This would work for any A:

pureList(1)
// res5: List[Int] = List(1)

pureList("a")
// res6: List[String] = List("a")

What Rúnar pointed out in 2010 is that Scala does not have a first-class notion for this.

Now say we want to take such a function as an argument to another function. With just rank-1 polymorphism, we can’t do this:

def usePolyFunc[A, B](f: A => List[A], b: B, s: String): (List[B], List[String]) =
  (f(b), f(s))
// error: type mismatch;
//  found   : b.type (with underlying type B)
//  required: A
//   (f(b), f(s))
//      ^
// error: type mismatch;
//  found   : s.type (with underlying type String)
//  required: A
//   (f(b), f(s))
//            ^

This is also what Launchbury and SPJ pointed out that Haskell cannot do in State Threads in 1994:

runST :: ∀a. (∀s. ST s a) -> a

This is not a Hindley-Milner type, because the quantifiers are not all at the top level; it is an example of rank-2 polymorphism.

Back to Rúnar:

It’s a type error because, B and String are not A. That is, the type A is fixed on the right of the quantifier [A, B]. We really want the polymorphism of the argument to be maintained so we can apply it polymorphically in the body of our function. Here’s how that might be expressed if Scala had rank-n types:

def usePolyFunc[B](f: (A => List[A]) forAll { A }, b: B, s: String): (List[B], List[String]) =
  (f(b), f(s))

So what we do is represent a rank-2 polymorphic function with a new trait that accepts a type argument in its apply method:

trait ~>[F[_], G[_]] {
  def apply[A](a: F[A]): G[A]
}

This is the same as FunctionK, or FunctionK is the same as ~>. Next, in a brilliant move Rúnar lifts A to F[_] using Id datatype:

We can now model a function that takes a value and puts it in a list, as a natural transformation from the identity functor to the List functor:

val pureList: Id ~> List = λ[Id ~> List](List(_))
// pureList: Id ~> List = repl.MdocSession3@6e515b56

def usePolyFunc[B](f: Id ~> List, b: B, s: String): (List[B], List[String]) =
  (f(b), f(s))

usePolyFunc(pureList, 1, "x")
// res9: (List[Int], List[String]) = (List(1), List("x"))

Yes. We now managed to pass polymorphic function around. I am guessing that rank-2 polymorphism was all the rage in part because it was advertised as the foundation to ensure typesafe access to resources in State Threads and other papers that came after it.

FunctionK in MonadCancel 

If we look at MonadCancel again, there’s FunctionK:

trait MonadCancel[F[_], E] extends MonadError[F, E] {
  def rootCancelScope: CancelScope

  def forceR[A, B](fa: F[A])(fb: F[B]): F[B]

  def uncancelable[B](body: Poll[F] => F[B]): F[B]

  ....
}

In the above, Poll[F] is actually a type alias for F ~> F:

trait Poll[F[_]] extends (F ~> F)

In other words, for all A F[A] would return F[A].

import cats.effect.IO

lazy val program = IO.uncancelable { poll =>
  poll(IO.canceled) >> IO.println("nope again")
}

In the above, IO must give us a function that works for any type A, and as we know from Rúnar’s post rank-1 polymorphism won’t work. Imagine if it were:

def uncancelable[A, B](body: F[A] => F[A] => F[B]): F[B]

This might work one call of poll(...), but within IO.uncancelable { ... } you should be able to call poll(...) multiple times:

lazy val program2: IO[Int] = IO.uncancelable { poll =>
  poll(IO.println("a")) >> poll(IO.pure("b")) >> poll(IO.pure(1))
}

So really poll(...) is ∀A. IO[A] => IO[A], or IO ~> IO.

Resource datatype 

Rúnar closed Higher-Rank Polymorphism in Scala with:

I wonder if we can use this [encoding of rank-2 polymorphic function] to get static guarantees of safe resource access, as in the SIO monad detailed in Lightweight Monadic Regions.

Cats Effect provides Resource datatype, which might work like Oleg Kiselyov and Chung-chieh Shan’s Lightweight Monadic Regions paper. In short, it’s a datatype encoding of MonadCancel we looked at in day 18, but easier to use.

The simplest way to construct a Resource is with Resource.make and the simplest way to consume a resource is with Resource#use. Arbitrary actions can also be lifted to resources with Resource.eval:

object Resource {
  def make[F[_], A](acquire: F[A])(release: A => F[Unit]): Resource[F, A]

  def eval[F[_], A](fa: F[A]): Resource[F, A]

  def fromAutoCloseable[F[_], A <: AutoCloseable](acquire: F[A])(
      implicit F: Sync[F]): Resource[F, A] =
    Resource.make(acquire)(autoCloseable => F.blocking(autoCloseable.close()))
}

sealed abstract class Resource[F[_], +A] {
  def use[B](f: A => F[B]): F[B]
}

Lightweight Monadic Regions:

We use the following motivating example inspired by real life:

1. open two files for reading, one of them a configuration file;
2. read the name of an output file (such as the log file) from the configuration file;
3. open the output file and zip the contents of both input files into the output file;
4. close the configuration file;
5. copy the rest, if any, of the other input file to the output file.

Here’s a program that reads from the first line of a text file:

import cats._, cats.syntax.all._
import cats.effect.{ IO, MonadCancel, Resource }
import java.io.{ BufferedReader, BufferedWriter }
import java.nio.charset.StandardCharsets
import java.nio.file.{ Files, Path, Paths }

def bufferedReader(path: Path): Resource[IO, BufferedReader] =
  Resource.fromAutoCloseable(IO.blocking {
    Files.newBufferedReader(path, StandardCharsets.UTF_8)
  })
  .onFinalize { IO.println("closed " + path) }

lazy val program: IO[String] = {
  val r0 = bufferedReader(Paths.get("docs/19/00.md"))
  r0 use { reader0 =>
    IO.blocking { reader0.readLine }
  }
}

scala> {
         import cats.effect.unsafe.implicits._
         program.unsafeRunSync()
       }
closed docs/19/00.md
val res0: String = ---

Here’s another program that writes text into a file:

def bufferedWriter(path: Path): Resource[IO, BufferedWriter] =
  Resource.fromAutoCloseable(IO.blocking {
    Files.newBufferedWriter(path, StandardCharsets.UTF_8)
  })
  .onFinalize { IO.println("closed " + path) }

lazy val program2: IO[Unit] = {
  val w0 = bufferedWriter(Paths.get("/tmp/Resource.txt"))
  w0 use { writer0 =>
    IO.blocking { writer0.write("test\n") }
  }
}

{
  import cats.effect.unsafe.implicits._
  program2.unsafeRunSync()
}

This created a text file named /tmp/Resource.txt. Thus far the resource management aspect has been trivial. The actual problem presented by Oleg and Chung-chieh Shan is more complicated because the name of the log file is read from the config file, but it outlives the life cycle of the config file.

def inner(input0: BufferedReader, config: BufferedReader): IO[(BufferedWriter, IO[Unit])] = for {
  fname <- IO.blocking { config.readLine }
  w0 = bufferedWriter(Paths.get(fname))

  // do the unsafe allocated
  p <- w0.allocated
  (writer0, releaseWriter0) = p
  _ <- IO.blocking { writer0.write(fname + "\n") }
  - <-
    (for {
      l0 <- IO.blocking { input0.readLine }
      _  <- IO.blocking { writer0.write(l0 + "\n") }
      l1 <- IO.blocking { config.readLine }
      _  <- IO.blocking { writer0.write(l1 + "\n") }
    } yield ()).whileM_(IO.blocking { input0.ready && config.ready })
} yield (writer0, releaseWriter0)

lazy val program3: IO[Unit] = {
  val r0 = bufferedReader(Paths.get("docs/19/00.md"))
  r0 use { input0 =>
    MonadCancel[IO].bracket({
      val r1 = bufferedReader(Paths.get("src/main/resources/a.conf"))
      r1 use { config => inner(input0, config) }
    })({ case (writer0, _) =>
      (for {
        l0 <- IO.blocking { input0.readLine }
        _  <- IO.blocking { writer0.write(l0 + "\n") }
      } yield ()).whileM_(IO.blocking { input0.ready })
    })({
      case (_, releaseWriter0) => releaseWriter0
    })
  }
}

To avoid closing the log file, I’m using Resource#allocated method, and to make sure it would eventually be closed I’m using MonadCancel[IO].bracket. Here’s what happens when we run this:

scala> {
         import cats.effect.unsafe.implicits._
         program3.unsafeRunSync()
       }
closed src/main/resources/a.conf
closed /tmp/zip_test.txt
closed docs/19/00.md

We see that the config file is closed before everything else.

So we were able to implement the example by cheating a bit, but it shows the flexibility of Resource.

Resource as Monad 

program3 got complicated, but more often than not we can acquire and release some resources together.

lazy val program4: IO[String] = (
  for {
    r0 <- bufferedReader(Paths.get("docs/19/00.md"))
    r1 <- bufferedReader(Paths.get("src/main/resources/a.conf"))
    w1 <- bufferedWriter(Paths.get("/tmp/zip_test.txt"))
  } yield (r0, r1, w1)
).use { case (intput0, config, writer0) =>
  IO.blocking { intput0.readLine }
}

{
  import cats.effect.unsafe.implicits._
  program4.unsafeRunSync()
}
// res1: String = "---"

In the above, Resources are combined into one monadically, and then used.

Resource cancellation 

To make sure the resources are cancelled during usage, let’s write a demo application that would print . forever, and cancel the program using Ctrl-C:

import cats._, cats.syntax.all._
import cats.effect.{ ExitCode, IO, IOApp, Resource }
import java.io.{ BufferedReader, BufferedWriter }
import java.nio.charset.StandardCharsets
import java.nio.file.{ Files, Path, Paths }

object Hello extends IOApp {
  def bufferedReader(path: Path): Resource[IO, BufferedReader] =
    Resource.fromAutoCloseable(IO.blocking {
      Files.newBufferedReader(path, StandardCharsets.UTF_8)
    })
    .onFinalize { IO.println("closed " + path) }

  override def run(args: List[String]): IO[ExitCode] =
    program.as(ExitCode.Success)

  lazy val program: IO[String] = (
    for {
      r0 <- bufferedReader(Paths.get("docs/19/00.md"))
      r1 <- bufferedReader(Paths.get("src/main/resources/a.conf"))
    } yield (r0, r1)
  ).use { case (intput0, config) =>
    IO.print(".").foreverM
  }
}

And here’s the result of running the app:

$ java -jar target/scala-2.13/herding-cats-assembly-0.1.0-SNAPSHOT.jar
..................................................................................................................................................................................................................................................................................................................................................................................................................................................................................^C............................................................................................................................................................................................................................................closed src/main/resources/a.conf
closed docs/19/00.md

Great. Resources are correctly closed.

Note that this is different from Resource forming MonadCancel, since it’s happening within use { ... }. We can look at the definition of use to understand this better:

  /**
   * Allocates a resource and supplies it to the given function.
   * The resource is released as soon as the resulting `F[B]` is
   * completed, whether normally or as a raised error.
   *
   * @param f the function to apply to the allocated resource
   * @return the result of applying [F] to
   */
  def use[B](f: A => F[B])(implicit F: MonadCancel[F, Throwable]): F[B] =
    fold(f, identity)

In this case I think Ctrl-C is handled by IO, and use { ... } guarantees to release the resource when f fails.

Ref as monad transformer 

There’s something difference about the datatypes like Ref and Resource:

abstract class Ref[F[_], A] extends RefSource[F, A] with RefSink[F, A] {
  /**
   * Modifies the current value using the supplied update function. If another modification
   * occurs between the time the current value is read and subsequently updated, the modification
   * is retried using the new value. Hence, `f` may be invoked multiple times.
   *
   * Satisfies:
   *   `r.update(_ => a) == r.set(a)`
   */
  def update(f: A => A): F[Unit]

  def modify[B](f: A => (A, B)): F[B]

  ....
}

In addition to the type parameter A like Option would take, Ref is also parameterized by F[_].

scala> :k -v cats.effect.Ref
cats.effect.Ref's kind is X[F[A1],A2]
(* -> *) -> * -> *
This is a type constructor that takes type constructor(s): a higher-kinded type.

These are monad transformers that take the effects type F as parameter. We can actually put another F like SyncIO:

import cats._, cats.syntax.all._
import cats.effect.{ IO, Ref, SyncIO }

lazy val program: SyncIO[Int] = for {
  r <- Ref[SyncIO].of(0)
  x <- r.get
} yield x

Resource as monad transformer 

We could probably make resource parametric on F[_]:

import cats.effect.{ IO, MonadCancel, Resource, Sync }
import java.io.BufferedReader
import java.nio.charset.{ Charset, StandardCharsets }
import java.nio.file.{ Files, Path, Paths }

def bufferedReader[F[_]: Sync](path: Path, charset: Charset): Resource[F, BufferedReader] =
  Resource.fromAutoCloseable(Sync[F].blocking {
    Files.newBufferedReader(path, charset)
  })

lazy val r0: Resource[SyncIO, BufferedReader] = bufferedReader[SyncIO](Paths.get("/tmp/foo"), StandardCharsets.UTF_8)

On most of the monad transformers there is mapK(...) method that takes FunctionK to transform it to another G[_]. If we can define a ~> from one effect type to another, we can transform the resource, which is radical:

lazy val toIO = λ[SyncIO ~> IO](si => IO.blocking { si.unsafeRunSync() })

lazy val r1: Resource[IO, BufferedReader] = r0.mapK(toIO)

That’s it for today.